No CrossRef data available.
Published online by Cambridge University Press: 21 December 2020
I show that the logic 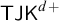 $\textsf {TJK}^{d+}$
, one of the strongest logics currently known to support the naive theory of truth, is obtained from the Kripke semantics for constant domain intuitionistic logic by (i) dropping the requirement that the accessibility relation is reflexive and (ii) only allowing reflexive worlds to serve as counterexamples to logical consequence. In addition, I provide a simplified natural deduction system for
$\textsf {TJK}^{d+}$
, one of the strongest logics currently known to support the naive theory of truth, is obtained from the Kripke semantics for constant domain intuitionistic logic by (i) dropping the requirement that the accessibility relation is reflexive and (ii) only allowing reflexive worlds to serve as counterexamples to logical consequence. In addition, I provide a simplified natural deduction system for
 $\textsf {TJK}^{d+}$
, in which a restricted form of conditional proof is used to establish conditionals.
$\textsf {TJK}^{d+}$
, in which a restricted form of conditional proof is used to establish conditionals.