No CrossRef data available.
Article contents
Aristotle and Corruptibility
A Discussion of Aristotle De Caelo I, xii
Published online by Cambridge University Press: 24 October 2008
Extract
(5) ἆρ' 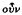 ∈ἰ kaì ⋯γ ∈´νητον (282 a 25) … πρòς τò ɸθαρτόν, ⋯ϕ' ᾧΘ (283 a 3). Aristotle claims so far to have proved that the eternal is incorruptible and that it is ungenerated. He has still to prove the converse of each of these propositions, namely, that whatever is incorruptible is eternal and that whatever is ungenerated is eternal also. After putting the thesis in question form he gives a further definition of ⋯γ∈´νητος and ἄɸθαρτος in the parenthesis of 282 a 27–30. Unfortunately in both cases he uses the assertoric form of the definiens, although in chapter 11 he had used a modal form in the relevant passages (cf. kυρίως 280 b 32 and 282 a 27); but this confusion does not seem to affect the immediate trend of the argument. He then (282 a 30—b 1) shows that his thesis follows necessarily from the convertibility of ⋯γ∈´νητος and ἄɸθαρτος. The additional premiss that is necessary in order to secure this inference, namely, that that which is both ungenerated and incorruptible is eternal, is clear from the definition of the terms. It is also clear from the convertibility of ɸθαρτóς and γ∈ νητóς, which itself is entailed by the supposed convertibility of their contradictories. This last inference seems too trivial to deserve a mention, but Aristotle devotes 282 b 2–5 to proving it. Then, having demonstrated to his satisfaction that the convertibility of ἄɸθαρτος and ⋯γ∈´νητος necessarily implies the eternity of both the incorruptible and the ungenerated, he adds, for good measure, that if the terms are not convertible the implication is no longer necessary (282 b 5–7).
∈ἰ kaì ⋯γ ∈´νητον (282 a 25) … πρòς τò ɸθαρτόν, ⋯ϕ' ᾧΘ (283 a 3). Aristotle claims so far to have proved that the eternal is incorruptible and that it is ungenerated. He has still to prove the converse of each of these propositions, namely, that whatever is incorruptible is eternal and that whatever is ungenerated is eternal also. After putting the thesis in question form he gives a further definition of ⋯γ∈´νητος and ἄɸθαρτος in the parenthesis of 282 a 27–30. Unfortunately in both cases he uses the assertoric form of the definiens, although in chapter 11 he had used a modal form in the relevant passages (cf. kυρίως 280 b 32 and 282 a 27); but this confusion does not seem to affect the immediate trend of the argument. He then (282 a 30—b 1) shows that his thesis follows necessarily from the convertibility of ⋯γ∈´νητος and ἄɸθαρτος. The additional premiss that is necessary in order to secure this inference, namely, that that which is both ungenerated and incorruptible is eternal, is clear from the definition of the terms. It is also clear from the convertibility of ɸθαρτóς and γ∈ νητóς, which itself is entailed by the supposed convertibility of their contradictories. This last inference seems too trivial to deserve a mention, but Aristotle devotes 282 b 2–5 to proving it. Then, having demonstrated to his satisfaction that the convertibility of ἄɸθαρτος and ⋯γ∈´νητος necessarily implies the eternity of both the incorruptible and the ungenerated, he adds, for good measure, that if the terms are not convertible the implication is no longer necessary (282 b 5–7).
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1966
References
Page 203 note 1 This concludes the discussion begun in Religious Studies, October 1965.
Page 203 note 2 The ἢ of 282 a 30 has been misunderstood. Stocks (n. 5) and Aquinas (lectio xxvii, n. 7) both take it as introducing a further, alternative, argument to prove that everything ungenerated or incorruptible is eternal. But we have so far had no such argument, although Stocks refers to the proof ‘which preceded the parenthesis (sc. of 282 a 27–30)’ and Aquinas (ibid. n. 6, cf. lectio sq. n. 4, ‘quod tamen supra ostensum est’, which the Leonine edd. take as referring to lectio xxvii, n. 6) seems to regard the definitions contained in the parenthesis as themselves constituting a proof. The ἢ in fact indicates that instead of proving directly the thesis proposed in 282 a 25–6, Aristotle intends to prove it indirectly via the convertibility of ἄφθαρτος and ἄγ⋯νητος.
Page 203 note 3 The repetition of ⋯ν⋯γκη in 282 b 2 (cf. 31–32) shows that κα⋯ γ⋯ρ àνáγκη, ∊ì φθαρτόν, γενητόν is still part of the apodosis of the conditional whose protasis is given in 282 a 30–31. Aquinas could hardly have been expected to gather this from his Latin version, and as a result makes 282 b 1 the start of a new lectio, thus completely misconstruing this part of the argument. Stocks and Guthrie, however, also failed to notice this, despite the correct exegesis of Simplicius (p. 337, 25, sq.). This leads both of them into queer interpretations of ύπόκειται and ύπέκειτο (282 b 3, 5). Both regard these words as referring back to 281 b 25, sqq., which is irrelevant, when in fact they refer to the protasis in 282 a 30, sqq. Guthrie actually mistranslates them as ‘we have already said’. Unfortunately they go on to lay the blame for their failure to understand the passage on Aristotle himself (‘needlessly complicated’, Stocks, n. 1 ad loc.; ‘typically disjointed’, Guthrie, p. 118, n. f.).
Page 204 note 1 With Alexander and Simplicius, q.v. pp. 343 sq.
Page 204 note 2 Aquinas's objection is raised and answered in lectio xxviii, n. 8.
Page 205 note 1 Cf. Simplicius, p. 346, 23 sqq. Aquinas regards this latter theory as a corollary of the former, and attributes both to Plato, ‘qui posuit mundum genitum sed incorruptibilem, et ex consequenti posuit quod illud inordinatum ex quo mundus est genitus, fuerit ingenitum sed corruptibile’ (lectio xxix, n. 2).
Page 206 note 1 Lectio xxix, n. 5.
Page 206 note 2 Lectio xxix, n. 8.
Page 206 note 3 Lectio xxix, n. 5.
Page 207 note 1 For this view of Aristotle's cf. MissAnscombe's, ‘Aristotle and the Sea Battle’, Mind (1956), pp. 1–15.CrossRefGoogle Scholar
Page 207 note 2 I am grateful to Mr Geach for pointing this out to me.
Page 207 note 3 Cf Bocheński, op cit. pp. 673 sq.; Prior, , Formal Logic, p. 185.Google Scholar
Page 208 note 1 Lectio, xxix, n. 12.
Page 208 note 2 Op. cit. p. 127, 6–16.
Page 209 note 1 Vide supra, p. 204.
Page 209 note 2 Vide supra, p. 97.
Page 211 note 1 Vide supra, p. 97. I refer to them hereafter as ‘(a)’ and ‘(b)’ respectively.
Page 211 note 2 Vide supra, p. 209.
Page 211 note 3 Metaphysics Θ, 3, 1047 a 13 does not, it seems to me, ‘state explicitly’, as Hintikka ((a) p. 72) says it does, the principle that that which never is is impossible. Rather, it states the harmless converse of this principle, namely, that what is impossible never is and never will be. Hintikka translates ‘⋯σήµχιυ∈υ’ somewhat tendentiously as ‘denotes precisely’. ‘Indicates’ would be a better translation. Again, ibid. 4, 1047 b 3–9, is a difficult passage which cannot with certainty be interpreted as supporting Hintikka's view. The quotation he gives from this passage ((a) p. 71) gives the translation of an emendation by Zeller which has no MS. support. Without this emendation the argument of the passage as a whole seems to me to be directed against those who hold that what never is is impossible: it is on their view that, according to Aristotle, the incommensurability of the diagonal is reduced to the assertion that no one ever will find a unit by which to measure both it and the side.
Page 212 note 1 As indeed would Aquinas. Commenting on 283 b 17 sqq. he remarks (op cit. lectio xxix, n. 11), ‘Et dicit quod etiam per rationem naturalem, et non per rationem universalem, idest logicam vel metaphysicam, sicut in praecedentibus, potest considerari…’.
Page 213 note 1 Thus the ἄλλοι λόγοι referred to at Metaphysics N, 1088 b 24 are most probably, as Alexander thought, these arguments in the De Caelo.
Page 213 note 2 Vide supra, pp. 98 sq., 102 sqq.
Page 213 note 3 Aristotle's Prior and Posterior Analytics, A Revised Text with Introduction and Commentary by Ross, W. D. (Oxford, 1949), p. 23.Google Scholar
Page 213 note 4 Aristotle's Physics, A Revised Text with Introduction and Commentary by Ross, W. D. (Oxford, 1936), p. 9.Google Scholar
Page 214 note 1 While on the subject of the dating of the philosophical works with which we have been concerned, it might be of interest to note that Aquinas's commentary on the De Caelo is dated in the last three years of his life. It is therefore not surprising that the doubt he there casts (vide supra, P. 99) on the validity of Aristotle's reasoning should have no effect on the use he makes elsewhere of Aristotle's conclusion, e g. in the Prima Pars, written at least six years earlier. Again, I have no knowledge of the relative dates of Buridan's commentary, from which I have previously quoted (vide supra, pp. 101 sq.), and of his Consequentiae, to which Hintikka refers ((a) p. 78, n. 1). But Hintikka notes the ‘big step towards the modern separation of modal and temporal notions’ which the rejection of the Aristotelian view by Ockham (and Buridan) represents. He adds, ‘How and why the change took place remains to be investigated’. Commentaries by medieval logicians on the De Caelo might be a good place to begin the investigation.
Page 214 note 2 It might be maintained that it is a natural tendency of this kind which Aquinas has in mind in his use of the phrase ‘possibilia esse et non esse’ in the Tertia Via.


