Bilateral oligopoly is a simple model of exchange in which a finite set of sellers seek to exchange the goods they are endowed with for money with a finite set of buyers, and no price-taking assumptions are imposed. If trade takes place via a strategic market game bilateral oligopoly can be thought of as two linked proportional-sharing contests: in one the sellers share the aggregate bid from the buyers in proportion to their supply and in the other the buyers share the aggregate supply in proportion to their bids. The analysis can be separated into two “partial games”. First, fix the aggregate bid at B; in the first partial game the sellers contest this fixed prize in proportion to their supply and the aggregate supply in the equilibrium of this game is 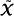(B). Next, fix the aggregate supply at X; in the second partial game the buyers contest this fixed prize in proportion to their bids and the aggregate bid in the equilibrium of this game is (X). The analysis of these two partial games takes into account competition within each side of the market. Equilibrium in bilateral oligopoly must take into account competition between sellers and buyers and requires, for example, ((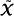B)) = B. When all traders have Cobb-Douglas preferences 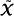(B) does not depend on B and (X) does not depend on X: whilst there is competition within each side of the market there is no strategic interdependence between the sides of the market. The Cobb-Douglas assumption provides a tractable framework in which to explore the features of fully strategic trade but it misses perhaps the most interesting feature of bilateral oligopoly, the implications of which are investigated.

L'oligopole bilatéral est une structure de marché dans laquelle un nombre fini de vendeurs cherchent à échanger les biens qu'ils possèdent contre de la monnaie détenue par un nombre fini d'acheteurs. Lorsque les échanges sont organisés dans le contexte d'un jeu stratégique de marché, l'oligopole bilatéral peut être analysé comme un jeu de marché divisé en deux sous-jeux liés. Fixons d'abord la quantité des stratégies agrégées des acheteurs à B; dans le premier jeu partiel la quantité offerte agrégée à l'équilibre est alors donnée par 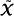(B). Fixons ensuite la quantité offerte agrégée à X; dans le deuxième jeu partiel, la stratégie d'achat agrégée est donc donnée par (X). Ces deux jeux partiels prennent en considération, dans chaque cas, les interactions au sein d'un même côté du marché. Or, le marché d'oligopole bilatéral met aussi en évidence des interactions entre les deux côtés de ce marché, et l'équilibre requiert notamment 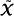= B. Lorsque tous les agents ont des préférences représentées par des fonctions d'utilité de type Cobb-Douglas, 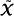(B) ne dépend pas de B et (X) ne dépend pas de X; il n'y a donc pas d'interdépendance stratégique entre les agents appartenant aux deux côtés du marché. Le cas d'une économie Cobb-Douglas fournit un cadre d'analyse utile pour étudier l'échange stratégique mais ne peut rendre compte de toutes les propriétés de l'échange en oligopole bilatéral. Certaines de ces propriétés sont étudiées dans l'article.