In this paper, the identification of stochastic regular languages is addressed. For this purpose, we propose a class of algorithms which allow for the identification of the structure of the minimal stochastic automaton generating the language. It is shown that the time needed grows only linearly with the size of the sample set and a measure of the complexity of the task is provided. Experimentally, our implementation proves very fast for application purposes.

Ordered binary decision diagrams are an important data structure for the representation of Boolean functions. Typically, the underlying variable ordering is used as an optimization parameter. When finite state machines are represented by OBDDs the state encoding can be used as an additional optimization parameter. In this paper, we analyze the influence of the state encoding on the OBDD-representations of counter-type finite state machines. In particular, we prove lower bounds, derive exact sizes for important encodings and construct a worst-case encoding which leads to exponential-size OBDDs.

We show that some classical P-complete problems can be solved efficiently in average NC. The probabilistic model we consider is the sample space of input descriptions of the problem with the underlying distribution being the uniform one. We present parallel algorithms that use a polynomial number of processors and have expected time upper bounded by (e ln 4 + o(1))log n, asymptotically with high probability, where n is the instance size.

If we consider words over the alphabet which is the set of all elements of a semigroup S, then such a word determines an element of S: the product of the letters of the word. S is strongly locally testable if whenever two words over the alphabet S have the same factors of a fixed length k, then the products of the letters of these words are equal. We had previously proved [19] that the syntactic semigroup of a rational language L is strongly locally testable if and only if L is both locally and piecewise testable. We characterize in this paper the variety of strongly locally testable semigroups with commuting idempotents and, using the theory of implicit operations on a variety of semigroups, we derive an elementary combinatorial description of the related variety of languages.

We introduce in this article a new method to calculate all absolute andrelatif primitive invariants of finite groups. This method is inspiredfrom K. Girstmair which calculate an absolute primitive invariant ofminimal degree.Are presented two algorithms, the first one enable us to calculate allprimitive invariants of minimal degree, and the second one calculate allabsolute or relative primitive invariants with distincts coefficients. Thiswork take place in Galois Theory and Invariant Theory.

We consider numeration systems where the base is anegative integer, or a complex number which is a root of anegative integer.We give parallel algorithms for addition in these numeration systems,from which we derive on-line algorithms realized by finite automata. A general construction relating addition in base βand addition in base βm is given.Results on addition in base $\beta=\sqrt[m]{b}$ 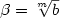, where b is a relative integer, follow.We also show that addition in base the golden ratiois computable by an on-line finite automaton, but is notparallelizable.