Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T15:33:23.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Theories of orders on the set of words

Published online by Cambridge University Press:  15 October 2005

Dietrich Kuske
Dietrich Kuske*
Affiliation:
Universität Leipzig, Germany; [email protected]
Get access

Abstract

It is shown that small fragments of the first-order theory of the subword order, the (partial) lexicographic path ordering on words, the homomorphism preorder, and the infix order are undecidable. This is in contrast to the decidability of the monadic second-order theory of the prefix order [M.O. Rabin, Trans. Amer. Math. Soc., 1969] and of the theory of the total lexicographic path ordering [P. Narendran and M. Rusinowitch, Lect. Notes Artificial Intelligence, 2000] and, in case of the subword and the lexicographic path order, improves upon a result by Comon & Treinen [H. Comon and R. Treinen, Lect. Notes Comp. Sci., 1994]. 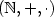Our proofs rely on the undecidability of the positive ∑1-theory of $(\mathbb N,+,\cdot)$ [Y. Matiyasevich, Hilbert's Tenth Problem, 1993] and on Treinen's technique [R. Treinen, J. Symbolic Comput., 1992] that allows to reduce Post's correspondence problem to logical theories.

Keywords

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 40 , Issue 1 , January 2006 , pp. 53 - 74
Copyright
© EDP Sciences, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

F. Baader and T. Nipkow, Term Rewriting and All That. Cambridge University Press (1998).
Björner, A., The Möbius function of subword order, in Invariant theory and tableaux, IMA Springer. Math. Appl. 19 (1990) 118–124.
Boudet, A. and Comon, H., About the theory of tree embedding, in TAPSOFT'93, Springer. Lect. Notes Comp. Sci. 668 (1993) 376–390. CrossRef
J.R. Büchi, Transfinite automata recursions and weak second order theory of ordinals, in Logic, Methodology and Philos. Sci., North Holland, Amsterdam (1965) 3–23.
Büchi, J.R. and Senger, S., Coding in the existential theory of concatentation. Archiv Math. Logik 26 (1986) 101–106. CrossRef
Comon, H. and Treinen, R., Ordering constraints on trees, in CAAP'94, Springer. Lect. Notes Comp. Sci. 787 (1994) 1–14. CrossRef
Comon, H. and Treinen, R., The first-order theory of lexicographic path orderings is undecidable. Theor. Comput. Sci. 176 (1997) 67–87. CrossRef
Daykin, D.E., To find all “suitable” orders of 0,1-vectors. Congr. Numer. 113 (1996) 55–60. Festschrift for C. St. J. A. Nash-Williams.
Dershowitz, N., Orderings for term rewriting systems. Theor. Comput. Sci. 17 (1982) 279–301. CrossRef
Durnev, V.G., Undecidability of the positive ∀∃3-theory of a free semigroup. Sibirsky Matematicheskie Jurnal 36 (1995) 1067–1080.
Farmer, F.D., Homotopy spheres in formal languages. Stud. Appl. Math. 66 (1982) 171–179. CrossRef
Finkel, A. and Schnoebelen, Ph., Well-structured transition systems everywhere! Theor. Comput. Sci. 256 (2001) 63–92. CrossRef
Gödel, K., Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 38 (1931) 173–198. CrossRef
Harju, T. and Illie, L., On quasi orders of words and the confluence property. Theor. Comput. Sci. 200 (1998) 205–224. CrossRef
Higman, G., Ordering by divisibility in abstract algebras. Proc. London Math. Soc. 2 (1952) 326–336. CrossRef
Kosub, S. and Wagner, K., The boolean hierarchy of NP-partitions, in STACS 2000, Springer. Lect. Notes Comp. Sci. 1770 (2000) 157–168. CrossRef
Kuske, D., Emptiness is decidable for asynchronous cellular machines, in CONCUR 2000. Springer. Lect. Notes Comp. Sci. 1877 (2000) 536–551. CrossRef
U. Leck, Nonexistence of a Kruskal-Katona type theorem for subword orders. Technical Report 98-06, Universität Rostock, Fachbereich Mathematik (1998).
M. Lothaire, Combinatorics on Words. Addison-Wesley (1983).
G.S. Makanin, The problem of solvability of equations in a free semigroup, Math. Sbornik, 103 (1977) 147–236. In Russian; English translation in: Math. USSR Sbornik 32 (1977).
Y. Matiyasevich, Hilbert's Tenth Problem. MIT Press (1993).
Narendran, P. and Rusinowitch, M., The theory of total unary rpo is decidable, in Computational Logic 2000, Springer. Lect. Notes Artificial Intelligence 1861 (2000) 660–672.
Rabin, M.O., Decidability of second-order theories and automata on infinite trees. Trans. Amer. Math. Soc. 141 (1969) 1–35.
Selivanov, V.L., Boolean hierarchy of partitions over reducible bases. Algebra and Logic 43 (2004) 77–109.
Treinen, R., A new method for undecidability proofs of first order theories. J. Symbolic Comput. 14 (1992) 437–458. CrossRef