Article contents
Some problems in automata theory which depend on the models of set theory
Published online by Cambridge University Press: 03 October 2011
Abstract
We prove that some fairly basic questions on automata reading infinite words depend on the models of the axiomatic system ZFC. It is known that there are only three possibilities for the cardinality of the complement of an ω-language \hbox{$L(\mathcal{A})$}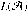 L(𝒜) accepted by a Büchi 1-counter automaton \hbox{$\mathcal{A}$}
L(𝒜) accepted by a Büchi 1-counter automaton \hbox{$\mathcal{A}$}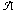 𝒜. We prove the following surprising result: there exists a 1-counter Büchi automaton \hbox{$\mathcal{A}$}
𝒜. We prove the following surprising result: there exists a 1-counter Büchi automaton \hbox{$\mathcal{A}$}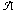 𝒜 such that the cardinality of the complement \hbox{$L(\mathcal{A})^-$}
𝒜 such that the cardinality of the complement \hbox{$L(\mathcal{A})^-$}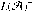 L(𝒜) − of the ω-language \hbox{$L(\mathcal{A})$}
L(𝒜) − of the ω-language \hbox{$L(\mathcal{A})$}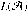 L(𝒜) is not determined by ZFC: (1) There is a model V1 of ZFC in which \hbox{$L(\mathcal{A})^-$}
L(𝒜) is not determined by ZFC: (1) There is a model V1 of ZFC in which \hbox{$L(\mathcal{A})^-$}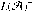 L(𝒜) − is countable. (2) There is a model V2 of ZFC in which \hbox{$L(\mathcal{A})^-$}
L(𝒜) − is countable. (2) There is a model V2 of ZFC in which \hbox{$L(\mathcal{A})^-$}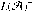 L(𝒜) − has cardinal 2ℵ0. (3) There is a model V3 of ZFC in which \hbox{$L(\mathcal{A})^-$}
L(𝒜) − has cardinal 2ℵ0. (3) There is a model V3 of ZFC in which \hbox{$L(\mathcal{A})^-$}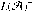 L(𝒜) − has cardinal ℵ1 with ℵ0 < ℵ1 < 2ℵ0.
L(𝒜) − has cardinal ℵ1 with ℵ0 < ℵ1 < 2ℵ0.
We prove a very similar result for the complement of an infinitary rational relation accepted by a 2-tape Büchi automaton ℬ. As a corollary, this proves that the continuum hypothesis may be not satisfied for complements of 1-counter ω-languages and for complements of infinitary rational relations accepted by 2-tape Büchi automata. We infer from the proof of the above results that basic decision problems about 1-counter ω-languages or infinitary rational relations are actually located at the third level of the analytical hierarchy. In particular, the problem to determine whether the complement of a 1-counter ω-language (respectively, infinitary rational relation) is countable is in Σ13\(Π12 ∪ Σ12). This is rather surprising if compared to the fact that it is decidable whether an infinitary rational relation is countable (respectively, uncountable).
Keywords
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 45 , Issue 4 , November 2011 , pp. 383 - 397
- Copyright
- © EDP Sciences 2011
References
Références
- 5
- Cited by


