We study infinite words u over an alphabet $\mathcal{A}$ satisfying the property $\mathcal{P} :~\mathcal{P}(n)+\mathcal{P}(n+1) = 1+ \#\mathcal{A}\ {\rm for\ any}\ n \in\mathbb{N}$ 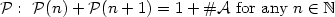, where $\mathcal{P}(n)$ 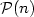denotes the number ofpalindromic factors of length n occurring in the language of u.We study also infinite words satisfying a strongerproperty $\mathcal{PE}$ 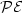: every palindrome of u has exactly one palindromic extension in u. For binary words, the properties $\mathcal{P}$ 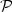and $\mathcal{PE}$ 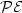coincide and these properties characterize Sturmian words, i.e.,words with the complexity C(n) = n + 1 for any $n \in \mathbb{N}$ 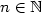. In this paper, we focus on ternary infinite wordswith the language closed under reversal. For such words u,we prove that if C(n) = 2n + 1 for any $n \in \mathbb{N}$ 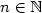,then u satisfies the property $\mathcal{P}$ 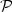andmoreover u is rich in palindromes. Also a sufficient condition for the property $\mathcal{PE}$ 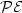is given.We construct a word demonstrating that $\mathcal{P}$ 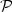on a ternaryalphabet does not imply $\mathcal{PE}$ .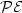