Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BERTONI, ALBERTO
MEREGHETTI, CARLO
and
PALANO, BEATRICE
2003.
GOLOMB RULERS AND DIFFERENCE SETS FOR SUCCINCT QUANTUM AUTOMATA.
International Journal of Foundations of Computer Science,
Vol. 14,
Issue. 05,
p.
871.
Bertoni, Alberto
Mereghetti, Carlo
and
Palano, Beatrice
2003.
Theoretical Computer Science.
Vol. 2841,
Issue. ,
p.
86.
Bertoni, Alberto
Mereghetti, Carlo
and
Palano, Beatrice
2005.
Small size quantum automata recognizing some regular languages.
Theoretical Computer Science,
Vol. 340,
Issue. 2,
p.
394.
Mereghetti, Carlo
and
Palano, Beatrice
2006.
The complexity of minimum difference cover.
Journal of Discrete Algorithms,
Vol. 4,
Issue. 2,
p.
239.
Mereghetti, Carlo
and
Palano, Beatrice
2006.
Quantum finite automata with control language.
RAIRO - Theoretical Informatics and Applications,
Vol. 40,
Issue. 2,
p.
315.
Bertoni, Alberto
Mereghetti, Carlo
and
Palano, Beatrice
2006.
Some formal tools for analyzing quantum automata.
Theoretical Computer Science,
Vol. 356,
Issue. 1-2,
p.
14.
Qiu, Daowen
and
Li, Lvzhou
2008.
An overview of quantum computation models: quantum automata.
Frontiers of Computer Science in China,
Vol. 2,
Issue. 2,
p.
193.
Li, Lvzhou
Qiu, Daowen
Zou, Xiangfu
Li, Lvjun
Wu, Lihua
and
Mateus, Paulo
2012.
Characterizations of one-way general quantum finite automata.
Theoretical Computer Science,
Vol. 419,
Issue. ,
p.
73.
Zheng, Shenggen
and
Qiu, Daowen
2014.
Computing with New Resources.
Vol. 8808,
Issue. ,
p.
231.
Giannakis, Konstantinos
Papalitsas, Christos
and
Andronikos, Theodore
2015.
Quantum automata for infinite periodic words.
p.
1.
Qiu, Daowen
Li, Lvzhou
Mateus, Paulo
and
Sernadas, Amilcar
2015.
Exponentially more concise quantum recognition of non-RMM regular languages.
Journal of Computer and System Sciences,
Vol. 81,
Issue. 2,
p.
359.
Bianchi, Maria Paola
Mereghetti, Carlo
and
Palano, Beatrice
2017.
Quantum finite automata: Advances on Bertoni's ideas.
Theoretical Computer Science,
Vol. 664,
Issue. ,
p.
39.
Mereghetti, Carlo
Palano, Beatrice
Cialdi, Simone
Vento, Valeria
Paris, Matteo G. A.
and
Olivares, Stefano
2020.
Photonic realization of a quantum finite automaton.
Physical Review Research,
Vol. 2,
Issue. 1,
Mereghetti, Carlo
Palano, Beatrice
and
Raucci, Priscilla
2024.
Unary Quantum Finite State Automata with Control Language.
Applied Sciences,
Vol. 14,
Issue. 4,
p.
1490.
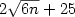 states inducing the event ap+b, for constants a>0, b ≥ 0, satisfying a+b ≥ 1. This fact is proved by designing an
algorithm which constructs the desired 1qfa in polynomial time. As a consequence, we get that any periodic language of period n can be
accepted with isolated cut point by a 1qfa with no more than $2\sqrt{6n}+26$
states inducing the event ap+b, for constants a>0, b ≥ 0, satisfying a+b ≥ 1. This fact is proved by designing an
algorithm which constructs the desired 1qfa in polynomial time. As a consequence, we get that any periodic language of period n can be
accepted with isolated cut point by a 1qfa with no more than $2\sqrt{6n}+26$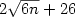 states. Our results give added evidence of the strength of measure-once
1qfa's with respect to classical automata.
states. Our results give added evidence of the strength of measure-once
1qfa's with respect to classical automata.