In this paper we investigate the average Horton-Strahler number of all possible tree-structures of binary tries. For that purpose we consider a generalization of extended binary trees where leaves are distinguished in order to represent the location of keys within a corresponding trie. Assuming a uniform distribution for those trees we prove that the expected Horton-Strahler number of a tree with α internal nodes and β leaves that correspond to a key is asymptotically given by $$\frac{4^{2\beta-\alpha}\log(\alpha)(2\beta-1)(\alpha+1)(\alpha+2){2\alpha+1\choose \alpha-1}}{8\sqrt{\pi}\alpha^{3/2}\log(2)(\beta-1)\beta{2\beta\choose \beta}^2}$$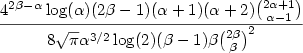 provided that α and β grow in some fixed proportion ρ when α → ∞ . A similar result is shown for trees with α internal nodes but with an arbitrary number of keys.