Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T02:02:27.747Z Has data issue: false hasContentIssue false
  • English
  • Français

On possible growths of arithmetical complexity

Published online by Cambridge University Press:  18 October 2006

Anna E. Frid
Anna E. Frid*
Affiliation:
Sobolev Institute of Mathematics SB RAS, Koptyug av., 4, 630090 Novosibirsk, Russia; [email protected]
Get access

Abstract

The arithmetical complexity of infinite words, defined by Avgustinovich, Fon-Der-Flaass and the author in 2000, is the number of words of length n which occur in the arithmetical subsequences of the infinite word. This is one of the modifications of the classical function of subword complexity, which is equal to the number of factors of the infinite word of length n. In this paper, we show that the orders of growth of the arithmetical complexity can behave as many sub-polynomial functions. More precisely, for each sequence u of subword complexity ƒu(n) and for each prime p ≥ 3 we build a Toeplitz word on the same alphabet whose arithmetical complexity is $a(n)=\Theta(n f_u(\lceil \log_p n \rceil))$.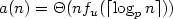

Keywords

Arithmetical complexityinfinite wordsubword complexityToeplitz wordbispecial words.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 40 , Issue 3: Word Avoidability Complexity And Morphisms (WACAM) , July 2006 , pp. 443 - 458
Copyright
© EDP Sciences, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P., Baake, M., Cassaigne, J. and Damanik, D., Palindrome complexity. Theoret. Comput. Sci. 292 (2003) 9–31. CrossRef
Allouche, J.-P. and Bousquet-Mélou, M., Canonical positions for the factors in paperfolding sequences. Theoret. Comput. Sci. 129 (1994) 263–278. CrossRef
J.-P. Allouche and J. Shallit, Automatic sequences: theory, applications, generalizations. Cambridge Univ. Press (2003).
S.V. Avgustinovich, J. Cassaigne and A.E. Frid, Sequences of low arithmetical complexity. submitted.
S.V. Avgustinovich, D.G. Fon-Der-Flaass and A.E. Frid, Arithmetical complexity of infinite words, in Words, Languages & Combinatorics III, Words, Languages & Combinatorics III, Singapore (2003), 51–62 World Scientific Publishing. ICWLC 2000, Kyoto, Japan, March (2000) 14–18.
Cassaigne, J., Complexité et facteurs spéciaux. Bull. Belg. Math. Soc. Simon Stevin 4 (1997) 67–88.
Cassaigne, J., Constructing infinite words of intermediate complexity, in Developments in Language Theory VI, edited by M. Ito and M. Toyama. Lect. Notes Comput. Sci. 2450 (2003) 173–184. CrossRef
J. Cassaigne and A. Frid, On arithmetical complexity of Sturmian words, accepted to WORDS'05.
Cassaigne, J. and Karhumäki, J., Toeplitz words, generalized periodicity and periodically iterated morphisms. Eur. J. Combin. 18 (1997) 497–510. CrossRef
Damanik, D., Local symmetries in the period doubling sequence. Discrete Appl. Math. 100 (2000) 115–121. CrossRef
Iványi, A., On the d-complexity of words, Ann. Univ. Sci. Budapest. Sect. Comput. 8 (1987) 69–90.
Ferenczi, S., Complexity of sequences and dynamical systems. Discrete Math. 206 (1999) 145–154. CrossRef
Frid, A., A lower bound for arithmetical complexity of Sturmian words. Siberian Electronic Math. Reports 2 (2005) 14–22.
Frid, A., Arithmetical complexity of symmetric D0L words. Theoret. Comput. Sci. 306 (2003) 535–542. CrossRef
Frid, A., Sequences of linear arithmetical complexity. Theoret. Comput. Sci. 339 (2005) 68–87. CrossRef
Kamae, T. and Zamboni, L., Sequence entropy and the maximal pattern complexity of infinite words. Ergodic Theory Dynam. Syst. 22 (2002) 1191–1199.
T. Kamae and L. Zamboni, Maximal pattern complexity for discrete systems. Ergodic Theory Dynam. Syst. 22 (2002), 1201–1214.
T. Kamae and H. Rao, Maximal pattern complexity over l letters. Eur. J. Combin., to appear.
Kamae, T. and Xue, Y.-M., Two dimensional word with 2k maximal pattern complexity. Osaka J. Math. 41 (2004) 257–265.
Koskas, M., Complexités de suites de Toeplitz. Discrete Math. 183 (1998) 161–183. CrossRef
Nakashima, I., Tamura, J. and Yasutomi, S., Modified complexity and *-Sturmian words. Proc. Japan Acad. Ser. A 75 (1999) 26–28. CrossRef
Nakashima, I., Tamura, J.-I. and Yasutomi, S.-I., *-Sturmian words and complexity. J. Théorie des Nombres de Bordeaux 15 (2003) 767–804. CrossRef
J.-E. Pin, Van der Waerden's theorem, in Combinatorics on words, edited by M. Lothaire. Addison-Wesley (1983) 39–54.
A. Restivo and S. Salemi, Binary patterns in infinite binary words, in Formal and Natural Computing, edited by W. Brauer et al. Lect. Notes Comput. Sci. 2300 (2002) 107–116.
Van der Waerden, B.L., Beweis einer Baudet'schen Vermutung. Nieuw. Arch. Wisk. 15 (1927) 212–216.