Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T20:32:54.809Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lower Bound For Reversible Automata

Published online by Cambridge University Press:  15 April 2002

Pierre-Cyrille Héam
Pierre-Cyrille Héam*
Affiliation:
LIAFA, Université Paris 7, 2 place Jussieu, 75251 Paris Cedex 05, France; ([email protected])
Get access

Abstract

A reversible automaton is a finite automaton in which eachletter induces a partial one-to-one map from the set of states intoitself. We solve the following problem proposed by Pin. Given an alphabet A, does there exist a sequence of languages K n on A which can be accepted by a reversible automaton, and such that the number of states of the minimal automaton of K n is in O(n), while the minimal number of states of a reversible automaton accepting K n is in O(ρ n ) for some ρ > 1? We give such an example with $\rho=\left(\frac{9}{8}\right)^{\frac{1}{12}}$ .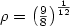

Keywords

Automataformal languagesreversible automata
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 34 , Issue 5 , September 2000 , pp. 331 - 341
Copyright
© EDP Sciences, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angluin, D., Inference of reversible languages. J. ACM 29 (1982) 741-765. CrossRef
J. Berstel, Transductions and Context-Free Languages. B.G. Teubner, Stuttgart (1979).
M. Hall, A topology for free groups and related groups. Ann. of Math. 52 (1950).
Hall, T., Biprefix codes, inverse semigroups and syntactic monoids of injective automata. Theoret. Comput. Sci. 32 (1984) 201-213. CrossRef
Herwig, B. and Lascar, D., Extending partial automorphisms and the profinite topology on free groups. Trans. Amer. Math. Soc. 352 (2000) 1985-2021. CrossRef
Margolis, S. and Meakin, J., Inverse monoids, trees, and context-free languages. Trans. Amer. Math. Soc. 335 (1993) 259-276.
S. Margolis, M. Sapir and P. Weil, Closed subgroups in pro-V topologies and the extension problem for inverse automata. Preprint (1998).
Margolis, S.W and Pin, J.-E., Languages and inverse semigroups, edited by J. Paredaens, Automata, Languages and Programming, 11th Colloquium. Antwerp, Belgium. Springer-Verlag, Lecture Notes in Comput. Sci. 172 (1984) 337-346. CrossRef
J.-E. Pin, Topologies for the free monoid. J. Algebra 137 (1991).
J.-E. Pin, On reversible automata, edited by I. Simon, in Proc. of Latin American Symposium on Theoretical Informatics (LATIN '92). Springer, Berlin, Lecture Notes in Comput. Sci. 583 (1992) 401-416; A preliminary version appeared in the Proceedings of ICALP'87, Lecture Notes in Comput. Sci. 267 .
Silva, P.V., On free inverse monoid languages. RAIRO: Theoret. Informatics Appl. 30 (1996) 349-378.
B. Steinberg, Finite state automata: A geometric approach. Technical Report, Univ. of Porto (1999).
B. Steinberg, Inverse automata and profinite topologies on a free group. Preprint (1999).