Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T17:03:33.215Z Has data issue: false hasContentIssue false
  • English
  • Français

The Helping Hierarchy

Published online by Cambridge University Press:  15 April 2002

Patrizio Cintioli  and
Riccardo Silvestri
Patrizio Cintioli
Affiliation:
Dipartimento di Matematica e Fisica, Università di Camerino, Via Madonna delle Carceri, 62032 Camerino (MC), Italy; ([email protected])
Riccardo Silvestri
Affiliation:
Dipartimento di Scienze dell'Informazione, Università di Roma "La Sapienza" , Via Salaria 113, 00198 Roma, Italy; ([email protected])
Get access

Abstract

Schöning [14] introduced a notion of helping and suggested the study of the class ${\rm P}_{\rm help}({\cal C})$ of the languages that can be helped by oracles in a given class ${\cal C}$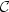. Later, Ko [12], in order to study the connections between helping and "witness searching" , introduced the notion of self-helping for languages. We extend this notion to classes of languages and show that there exists a self-helping class that we call SH which contains all the self-helping classes. We introduce the Helping hierarchy whose levels are obtained applying a constant number of times the operator ${\rm P}_{\rm help}(\cdot)$ to the set of all the languages. We show that the Helping hierarchy collapses to the k-th level if and only if SH is equal to the k-th level. We give characterizations of all the levels and use these to construct a relativized world in which the Helping hierarchy is infinite.

Keywords

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 35 , Issue 4 , July 2001 , pp. 367 - 377
Copyright
© EDP Sciences, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

V. Arvind, A Note on the Self-Witnessing Property of Computational Problems, Proc. 2nd Annual International Conference on Computing and Combinatorics (COCOON'96). Springer-Verlag, Lecture Notes in Comput. Sci. 1090 (1996) 241-249.
J.L. Balcázar, Self-reducibility, Proc. 4th Symposium on Theoretical Aspects of Computer Science. Springer-Verlag, Lecture Notes in Comput. Sci. 247 (1987) 136-147.
Balcázar, J.L., Self-reducibility structures and solutions of NP problems. Rev. Mat. Complut. 2 (1989) 175-184. CrossRef
D.P. Bovet and P. Crescenzi, Introduction to the Theory of Complexity. Prentice-Hall (1994).
J.L. Balcázar, J. Díaz and J. Gabarró, Structural Complexity I, Vol. 1. Springer-Verlag (1988).
J.L. Balcázar, J. Díaz and J. Gabarró, Structural Complexity II, Vol. 2. Springer-Verlag (1990).
J. Cai, L. Hemachandra and J. Viskoc, Promises Problems and Access to Unambiguous Computation, Proc. 17th Symposium on Mathematical Foundations of Computer Science. Springer-Verlag, Lecture Notes in Comput. Sci. 629 (1992) 162-171.
Cintioli, P. and Silvestri, R., Helping by Unambiguous Computation and Probabilistic Computation. Theory Comput. Syst. 30 (1997) 165-180. CrossRef
Cintioli, P. and Silvestri, R., Revisiting a Result of Ko. Inform. Process. Lett. 61 (1997) 189-194. CrossRef
M. Fellows and N. Koblitz, Self-witnessing polynomial time complexity and prima factorization, in Proc. 6th Structure in Complexity Theory Conference (1992) 107-110.
L. Hemachandra, Fault-Tolerance and Complexity, in Proc. 20th International Colloquium on Automata, Languages, and Programming. Springer-Verlag, Lecture Notes in Comput. Sci. (1993).
On Helping, K. Ko by Robust Oracle Machines. Theoret. Comput. Sci. 52 (1987) 15-36.
Ogihara, M., Helping, On by Parity-like Languages. Inform. Process. Lett. 54 (1995) 41-43. CrossRef
Schöning, U., Robust Algorithms: A Different Approach to oracles. Theoret. Comput. Sci. 40 (1985) 57-66. CrossRef