Published online by Cambridge University Press: 28 February 2011
We present a CAT (constant amortized time) algorithm for generating those partitions of n that are in the
ice pile model$\mbox{IPM}_k$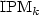 (n),
a generalization of the
sand pile model$\mbox{SPM}$
(n),
a generalization of the
sand pile model$\mbox{SPM}$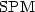 (n).
More precisely, for any fixed integer k, we show that
the negative lexicographic ordering naturally identifies a tree structure on the lattice
$\mbox{IPM}_k$
(n).
More precisely, for any fixed integer k, we show that
the negative lexicographic ordering naturally identifies a tree structure on the lattice
$\mbox{IPM}_k$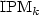 (n):
this lets us design an algorithm which generates all the ice piles of
$\mbox{IPM}_k$
(n):
this lets us design an algorithm which generates all the ice piles of
$\mbox{IPM}_k$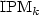 (n)
in amortized time
O(1)
and in space
O($\sqrt n$
(n)
in amortized time
O(1)
and in space
O($\sqrt n$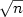 ).
).