In this paper we will deal with the balance properties of the infinite binary words associated to β-integers when β is a quadratic simple Pisot number. Those words are the fixed points of the morphisms of the type $\varphi(A)=A^pB$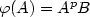, $\varphi(B)=A^q$ 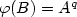for $p\in\mathbb N$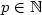, $q\in\mathbb N$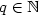, $p\geq q$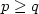, where $\beta=\frac{p+\sqrt{p^2+4q}}{2}$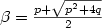. We will prove that such word is t-balanced with $t=1+\left[(p-1)/(p+1-q)\right]$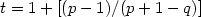. Finally, in the case that p < q it is known [B. Adamczewski, Theoret. Comput. Sci.273 (2002) 197–224] that the fixed point of the substitution $\varphi(A)=A^pB$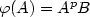, $\varphi(B)=A^q$ 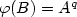is not m-balanced for any m. We exhibit an infinite sequence of pairs of words with the unbalance property.