Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T16:13:30.198Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Succinctness of Deterministic, Nondeterministic, Probabilistic and Quantum Finite Automata

Published online by Cambridge University Press:  15 August 2002

Carlo Mereghetti ,
Beatrice Palano  and
Giovanni Pighizzini
Carlo Mereghetti
Affiliation:
Dipartimento di Informatica, Sist. e Com., Università degli Studi di Milano – Bicocca, via Bicocca degli Arcimboldi 8, 20126 Milano, Italy; [email protected].
Beatrice Palano
Affiliation:
Dipartimento di Informatica, Università degli Studi di Torino, c.so Svizzera 185, 10149 Torino, Italy; [email protected].
Giovanni Pighizzini
Affiliation:
Dipartimento di Scienze dell'Informazione, Università degli Studi di Milano, via Comelico 39, 20135 Milano, Italy; [email protected].
Get access

Abstract

We investigate the succinctness of several kinds of unary automata by studying their state complexity in accepting the family {Lm } of cyclic languages, where Lm = akm | k ∈ N. 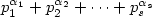In particular, we show that, for any m, the number of states necessary and sufficient for accepting the unary language L m with isolated cut point on one-way probabilistic finite automata is $p_1^{\alpha_1}+ p_2^{\alpha_2} +\cdots +p_s^{\alpha_s}$ , with $p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_s^{\alpha_s}$ 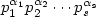being the factorization of m. To prove this result, we give a general state lower bound for accepting unary languages with isolated cut point on the one-way probabilistic model. Moreover, we exhibit one-way quantum finite automata that, for any m, accept L m with isolated cut point and only two states. These results are settled within a survey on unary automata aiming to compare the descriptional power of deterministic, nondeterministic, probabilistic and quantum paradigms.

Keywords

Deterministicnondeterministicprobabilisticquantum unaryfinite automata.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 35 , Issue 5 , September 2001 , pp. 477 - 490
Copyright
© EDP Sciences, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A. Ambainis, The complexity of probabilistic versus deterministic finite automata, in Proc. 7th International Symposium on Algorithms and Computation (ISAAC). Springer, Lecture Notes in Comput. Sci. 1178 (1996) 233-238.
A. Ambainisand R. Freivalds, 1-way quantum finite automata: Strengths, weaknesses and generalizations, in Proc. 39th Annual Symposium on Foundations of Computer Science (FOCS). IEEE Computer Society Press (1998) 332-342.
A. Brodskyand N. Pippenger, Characterizations of 1-way quantum finite automata, Techn. Rep. 99-03. Univ. of British Columbia, Dept. of Computer Science (1999).
Chandra, A., Kozenand, D. Stockmeyer, L., Alternation. J. ACM 28 (1981) 114-133. CrossRef
Chrobak, M., Finite automata and unary languages. Theoret. Comput. Sci. 47 (1986) 149-158. CrossRef
F. Gantmacher, Applications of Theory of Matrices. Interscience Pub., New York (1959).
J. Gruska, Quantum Computing. McGraw-Hill, London, New York (1999).
Gruska, J., Descriptional complexity issues in quantum computing. J. Autom. Lang. Comb 5 (2000) 191-218.
A. Kondacsand J. Watrous, On the power of quantum finite state automata, in Proc. 38th Annual Symposium on Foundations of Computer Science (FOCS). IEEE Computer Society Press (1997) 66-75.
J. Hopcroftand J. Ullman, Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Reading, MA (1979).
Ladner, R., Lipton, R. and Stockmeyer, L., Alternating pushdown and stack automata. SIAM J. Comput. 13 (1984) 135-155. CrossRef
Landau, E., Uber die Maximalordung der Permutationen gegebenen Grades. Archiv. der Math. und Phys. 3 (1903) 92-103.
E. Landau, Handbuch der lehre von der verteilung der primzahlen. I. Teubner, Leipzig, Berlin (1909).
Mereghettiand, C. Pighizzini, G., Two-Way automata simulations and unary languages. J. Autom. Lang. Comb. 5 (2000) 287-300.
Mereghettiand, C. Pighizzini, G., Optimal simulations between unary autom. SIAM J. Comput. 30 (2001) 1976-1992. CrossRef
A. Meyerand M. Fischer, Economy of description by automata, grammars, and formal systems, in Proc. 12th Annual Symposium on Switching and Automata Theory. East Lansing, Michigan (1971) 188-191.
M. Milaniand G. Pighizzini, Tight bounds on the simulation of unary probabilistic automata by deterministic automata, in Pre-Proc. Descriptional Complexity of Automata, Grammars and Related Structures (DCAGRS), Techn. Rep. 555. Univ. of Western Ontario, Canada, Dept. Comp. Sci., J. Autom. Lang. and Comb. (2000).
E. Moore, On the bounds for state-set size in the proofs of equivalence between deterministic, nondeterministic, and two-way finite automata. IEEE Trans. Comput. C-20 (1971) 1211-1214.
Mooreand, C. Crutchfield, J., Quantum automata and quantum grammars. Theoret. Comput. Sci. 237 (2000) 275-306.
A. Paz, Introduction to Probabilistic Automata. Academic Press, New York, London (1971).
Pin, J.E., Languages Accepted, On by finite reversible automata, in Proc. of the 14th International Colloquium on Automata, Languages and Programming (ICALP). Springer-Verlag, Lecture Notes in Comput. Sci. 267 (1987) 237-249. CrossRef
M. Rabin, Probabilistic automata. Inform. and Control 6 (1963) 230-245.
Rabinand, M. Scott, D., Finite automata and their decision problems. IBM J. Res. Develop. 3 (1959) 114-125. Also in: E.F. Moore, Sequential Machines: Selected Papers. Addison-Wesley, Reading, MA (1964).
Shepherdson, J., The reduction of two-way automata to one-way automata. IBM J. Res. Develop. 3 (1959) 198-200. Also in: E.F. Moore, Sequential Machines: Selected Papers. Addison-Wesley, Reading, MA (1964). CrossRef
Szalay, M., On the maximal order in S n and S * n . Acta Arithmetica 37 (1980) 321-331.
P. Turán, Combinatorics, partitions, group theory, edited by B. Serge, Colloquio Internazionale sulle Teorie Combinatorie. Acc. Naz. dei Lincei, Rome (1976) 181-200.