Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T02:24:47.942Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the number of squaresin a partial word with one hole

Published online by Cambridge University Press:  01 October 2009

Francine Blanchet-Sadri  and
Robert Mercaş
Francine Blanchet-Sadri
Affiliation:
Department of Computer Science, University of North Carolina, P.O. Box 26170, Greensboro, NC 27402–6170, USA; [email protected]
Robert Mercaş
Affiliation:
GRLMC, Universitat Rovira i Virgili, Departament de Filologies Romàniques, Av. Catalunya 35, Tarragona, 43002, Spain.
Get access

Abstract

A well known result of Fraenkel and Simpson states that the number of distinct squares in a word of length n is bounded by 2n since at each position there are at most two distinct squares whose last occurrence starts. In this paper, we investigate squares in partial words with one hole,or sequences over a finite alphabet that have a “do not know” symbol or “hole”. A square in a partial word over a given alphabet has the form uv where u is compatible with v, and consequently, such square is compatible with a number of words over the alphabet that are squares. Recently, it was shown that for partial words with one hole, there may be more than two squares that have their last occurrence starting at the same position. Here, we prove that if such is the case, then the length of the shortest square is at most half the length of the third shortest square.As a result, we show that the number of distinct squares compatible with factors of a partial word with one hole of length n is bounded by $\frac{7n}{2}$ .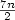

Keywords

Combinatorics on wordspartial wordssquares.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 43 , Issue 4 , October 2009 , pp. 767 - 774
Copyright
© EDP Sciences, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berstel, J. and Boasson, L., Partial words and a theorem of Fine and Wilf. Theoret. Comput. Sci. 218 (1999) 135–141. CrossRef
F. Blanchet-Sadri, Algorithmic Combinatorics on Partial Words. Chapman & Hall/CRC Press, Boca Raton, FL (2008).
Blanchet-Sadri, F. and Luhmann, D.K., Conjugacy on partial words. Theoret. Comput. Sci. 289 (2002) 297–312. CrossRef
F. Blanchet-Sadri, R. Mercaş and G. Scott, Counting distinct squares in partial words, edited by E. Csuhaj-Varju, Z. Esik, AFL 2008, 12th International Conference on Automata and Formal Languages, Balatonfüred, Hungary (2008) 122–133, www.uncg.edu/cmp/research/freeness
Blanchet-Sadri, F., Blair, D.D. and Lewis, R.V., Equations on partial words. RAIRO-Theor. Inf. Appl. 43 (2009) 23–39, www.uncg.edu/cmp/research/equations CrossRef
Fraenkel, A.S. and Simpson, J., How many squares can a string contain? J. Combin. Theory Ser. A 82 (1998) 112–120. CrossRef
Ilie, L., A simple proof that a word of length n has at most 2n distinct squares. J. Combin. Theory Ser. A 112 (2005) 163–164. CrossRef
Ilie, L., A note on the number of squares in a word. Theoret. Comput. Sci. 380 (2007) 373–376. CrossRef