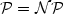This paper deals with lower bounds on the approximability of different subproblems of the TravelingSalesman Problem (TSP) which is known not to admit any polynomial time approximation algorithm in general(unless $\mathcal{P}=\mathcal{NP}$ ). First of all, we present an improved lower bound for the Traveling Salesman Problemwith Triangle Inequality, Delta-TSP for short. Moreover our technique, an extension of the method ofEngebretsen [11], also applies to the case of relaxed and sharpened triangle inequality,respectively, denoted $\Delta_\beta$ 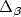-TSP for an appropriate β. In case of theDelta-TSP, we obtain a lowerbound of $\frac{3813}{3812}-\varepsilon$ 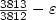on the polynomial-time approximability (for any small $\varepsilon> 0$ 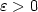), compared to the previous bound of $\frac{5381}{5380}-\varepsilon$ 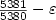in [11]. Incase of the $\Delta_\beta$ 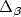-TSP, for the relaxed case ( $\beta> 1$ 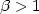) we present a lower bound of $\frac{3803+10\beta}{3804+8\beta}-\varepsilon$ 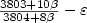, and for the sharpened triangle inequality( $\frac{1}{2}< \beta< 1$ 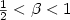), the lower bound is $\frac{7611+10\beta^2+5\beta}{7612+8\beta^2+4\beta}-\varepsilon$ 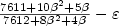. The latter result is of interestespecially since it shows that the TSP is $\mathcal{APX}$ 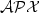-hard even if one comes arbitrarily close to the trivialcase that all edges have the same cost.