Published online by Cambridge University Press: 18 January 2008
We design algorithms of “optimal" data complexity for several natural problems about first-order queries on structures of bounded degree. For that purpose, we first introduce a framework to deal with logical or combinatorial problems R ⊂ I x O whose instances x ∈ I may admit of several solutions R(x) = {y ∈ O : (x,y) ∈ R}. One associates to such a problem several specific tasks: compute a random (for the uniform probability distribution) solution y ∈ R(x); enumerate without repetition each solution yj in some specific linear order y0 < y1 < ... < yn-1 where R(x) = {y0,...,yn-1}; compute the solution yj of rankj in the linear order <.
Algorithms of “minimal" data complexity are presented for the following problems: given any first-order formula $\varphi(\bar{v})$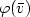 and any structure S of bounded degree:
(1) compute a random element of $\varphi(S)=\{\bar{a}: (S,\bar{a})\models\varphi(\bar{v})\}$
and any structure S of bounded degree:
(1) compute a random element of $\varphi(S)=\{\bar{a}: (S,\bar{a})\models\varphi(\bar{v})\}$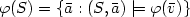 ;
(2) compute the jth element of $\varphi(S)$
;
(2) compute the jth element of $\varphi(S)$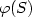 for some linear order of $\varphi(S)$
for some linear order of $\varphi(S)$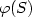 ;
(3) enumerate the elements of $\varphi(S)$
;
(3) enumerate the elements of $\varphi(S)$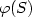 in lexicographical order.
More precisely, we prove that, for any fixed formula φ, the above problem (1) (resp. (2), (3)) can be computed within average constant time (resp. within constant time, with constant delay) after a linear (O(|S|)) precomputation. Our essential tool for deriving those complexity results is a normalization procedure of first-order formulas on bijective structures.
in lexicographical order.
More precisely, we prove that, for any fixed formula φ, the above problem (1) (resp. (2), (3)) can be computed within average constant time (resp. within constant time, with constant delay) after a linear (O(|S|)) precomputation. Our essential tool for deriving those complexity results is a normalization procedure of first-order formulas on bijective structures.