Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T19:20:33.196Z Has data issue: false hasContentIssue false
  • English
  • Français

Recherche à voisinage variable de graphes extrémaux 26. Nouveaux résultats sur la maille

Published online by Cambridge University Press:  08 October 2009

Mustapha Aouchiche ,
Odile Favaron  and
Pierre Hansen
Mustapha Aouchiche
Affiliation:
HEC Montréal, Qc, Canada; [email protected]
Odile Favaron
Affiliation:
Univ Paris-Sud, LRI, UMR 8623, Orsay, 91405, France. CNRS, Orsay, 91405, France; [email protected]
Pierre Hansen
Affiliation:
GERAD et HEC Montréal, Qc, Canada; [email protected]
Get access

Abstract

On étudie à l'aide du système AutoGraphiX 2 (AGX 2) des relations de la forme \[ \underline{b}_{n} \, \le \, g\,\oplus \,i\, \le \, \overline{b}_{n}\] 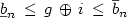où g désigne la maille d'un graphe G=(V, E), i un autre invariant parmi la distance moyenne $\overline{l}$ 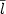, l'index λ1, l'indice de Randić R et le nombre de domination β, $\oplus$ 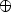désigne l'une des opérations+, -, ×, /, $\underline{b}_{n}$ 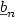et $\overline{b}_{n}$ 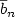des fonctions de l'ordre n du graphe qui bornent l'expression $g\oplus i$ 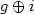et sont atteintes pour tout n (sauf éventuellement de très petites valeurs du fait des effets de bord). Les résultats prouvés ou discutés ci-dessous ont déjà été présentés, sousforme de conjectures, dans un article précédent paru dans RAIRO Recherche Opérationnelle [RAIRO Oper. Res. 39 (2005) 275–293].

Keywords

GraphAGXgirthdistanceRandićindexdomination.GrapheAGXmailledistanceRandićindexdomination.
Type
Research Article
Information
RAIRO - Operations Research , Volume 43 , Issue 4: ROADEF 07 , October 2009 , pp. 339 - 358
Copyright
© EDP Sciences, ROADEF, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Aouchiche, Comparaison automatisée d'invariants en théorie des graphes. Ph.D. Thesis, École Polytechnique de Montréal, February (2006). Disponible sur www.gerad.ca/ agx.
M. Aouchiche, G. Caporossi and P. Hansen, Variable neighborhood search for extremal graphs. 20. Automated comparison of graph invariants. MATCH Commun. Math. Comput. Chem. 58 (2007) 365–384.
M. Aouchiche, J.-M. Bonnefoy, A. Fidahoussen, G. Caporossi, P. Hansen, L. Hiesse, J. Lacheré and A. Monhait, Variable Neighborhood Search for Extremal Graphs. 14. The AutoGraphiX 2 System, in Global Optimization: From theory to implementation, edited by L. Liberti and N. Maculan, Springer (2006) 281–310.
M. Aouchiche and P. Hansen, Recherche à voisinage variable de graphes extrémaux. XIII. À propos de la maille. (French) RAIRO-Oper. Res. 39 (2005) 275–293.
M. Aouchiche, P. Hansen and M. Zheng, Variable neighborhood search for extremal graphs. 19. Further conjectures and results about the Randić index. MATCH Commun. Math. Comput. Chem. 58 (2007) 83–102.
B. Bollobás and P. Erdös, Graphs of extremal weights. Ars Combin. 50 (1998) 225–233.
Bondy, J.A. and Halberstam, F.Y., Parity theorems for paths and cycles in graphs. J. Graph Theory 10 (1986) 107–115. CrossRef
G. Caporossi and P. Hansen, Variable neighborhood search for extremal graphs. I. The AutGraphiX system. Disc. Math. 212 (2000) 29–44.
D. Cvetković, M. Doob and H. Sachs, Spectra of graphs – Theory and application. Academic Press, New York (1982).
Cvetković, D. and Rowlinson, P., Spectra of unicyclic graphs. Graphs and combinatorics 3 (1987) 7–23. CrossRef
C. Delorme, O. Favaron and D. Rautenbach, On the Randić index. Discrete Math. 257 (2002) 29–38.
F.M. Dong and K.M. Koh, The Sizes of Graph with Small Girth. Bull. Inst. Combin. Appl. 18 (1996) 33–44.
R.D. Dutton and R.C. Brigham, Edges in Graphs with Large Girth. Graphs Combin. 7 (1991) 315–321.
A.J. Hoffman, On Limit Points of Spectral Radii of Non-Negative Symmetric Integral Matrices, in Graph Theory and Applications. Lect. Notes Math. 303, edited by Y. Alavi, D.R. Lick, A.T. White, Springer-Verlag, Berlin (1972) 165–172.
Li, Q., and Feng, K.Q., On the largest eigenvalue of a graph. Acta Math. Appl. Sinica 2 (1979) 167–175.
G. Liu, Y. Zhu and J. Cai, On the Randić index of unicyclic graphs with girth g. MATCH Commun. Math. Comput. Chem. 58 (2007) 127–138.
Turán, P., An extremal problem in graph theory. Mat. Fiz. Lapok 48 (1941) 436–452.