Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T19:33:52.258Z Has data issue: false hasContentIssue false
  • English
  • Français

On co-bicliques

Published online by Cambridge University Press:  21 August 2007

Denis Cornaz
Denis Cornaz*
Affiliation:
Équipe Combinatoire, UFR 921, Case 189, Université Pierre et Marie Curie, 4 place Jussieu, 75252 Paris Cedex 05 France; [email protected]
Get access

Abstract

A co-biclique of a simple undirected graph G = (V,E) is the edge-set of two disjoint complete subgraphs of G.(A co-biclique is the complement of a biclique.)A subset F ⊆ E is an independent of G if there is a co-biclique B such that F ⊆ B, otherwise F is a dependent of G. This paper describes the minimal dependents of G. (A minimal dependent is a dependent C such that any proper subset of C is an independent.) It is showed that a minimum-cost dependent set of G can be determined in polynomial time for any nonnegative cost vector $x\in \mathbb Q_+^E$ 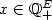. Based on this, we obtain a branch-and-cut algorithm for the maximum co-biclique problem which is, given a weight vector $w\in \mathbb Q_+^E$ 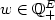, to find a co-biclique B of G maximizing w(B) = ∑e∈B we .

Keywords

Co-bicycliquesigned graphbranch-and-cut
Type
Research Article
Information
RAIRO - Operations Research , Volume 41 , Issue 3: Journées Polyèdres et Optimisation Combinatoire , July 2007 , pp. 295 - 304
Copyright
© EDP Sciences, ROADEF, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cornaz, D., A linear programming formulation for the maximum complete multipartite subgraph problem. Math. Program. B 105 (2006) 329–344. CrossRef
Cornaz, D. and Fonlupt, J., Chromatic characterization of biclique cover. Discrete Math. 306 (2006) 495–507. CrossRef
D. Cornaz and A.R. Mahjoub, The maximum induced bipartite subgraph problem with edge weights. SIAM J. on Discrete Math. to appear.
D. Cornaz, On forests, stable sets and polyhedra associated with clique partitions. Manuscript available on Optimization Online.
V. Jost, Ordonnancement chromatique : polyèdres, complexité et classification. Thèse de l'Université Joseph Fourier, Grenoble (2006).
Grötschel, M., Lovàsz, L. and Schrijver, A., The ellipsoid method and its consequences in combinatorial optimization. Combinatorica 1 (1981) 169–197. CrossRef
Monson, D., Pullman, N.J. and Rees, R., A survey of clique and biclique coverings and factorizations of (0,1)-matrices. Bull. I.C.A. 14 (1995) 17–86.
A. Schrijver, Combinatorial Optimization. Springer-Verlag, Berlin Heidelberg (2003).
A. Sebő, private communication.