Article contents
WALLABY pilot survey: The diversity of HI structural parameters in nearby galaxies
Published online by Cambridge University Press: 08 June 2023
Abstract
We investigate the diversity in the sizes and average surface densities of the neutral atomic hydrogen (H i) gas discs in 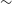 $\sim$280 nearby galaxies detected by the Widefield ASKAP L-band Legacy All-sky Blind Survey (WALLABY). We combine the uniformly observed, interferometric H i data from pilot observations of the Hydra cluster and NGC 4636 group fields with photometry measured from ultraviolet, optical, and near-infrared imaging surveys to investigate the interplay between stellar structure, star formation, and H i structural parameters. We quantify the H i structure by the size of the H i relative to the optical disc and the average H i surface density measured using effective and isodensity radii. For galaxies resolved by
$\sim$280 nearby galaxies detected by the Widefield ASKAP L-band Legacy All-sky Blind Survey (WALLABY). We combine the uniformly observed, interferometric H i data from pilot observations of the Hydra cluster and NGC 4636 group fields with photometry measured from ultraviolet, optical, and near-infrared imaging surveys to investigate the interplay between stellar structure, star formation, and H i structural parameters. We quantify the H i structure by the size of the H i relative to the optical disc and the average H i surface density measured using effective and isodensity radii. For galaxies resolved by 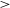 $>$
$>$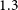 $1.3$ beams, we find that galaxies with higher stellar masses and stellar surface densities tend to have less extended H i discs and lower H i surface densities: the isodensity H i structural parameters show a weak negative dependence on stellar mass and stellar mass surface density. These trends strengthen when we limit our sample to galaxies resolved by
$1.3$ beams, we find that galaxies with higher stellar masses and stellar surface densities tend to have less extended H i discs and lower H i surface densities: the isodensity H i structural parameters show a weak negative dependence on stellar mass and stellar mass surface density. These trends strengthen when we limit our sample to galaxies resolved by 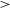 $>$2 beams. We find that galaxies with higher H i surface densities and more extended H i discs tend to be more star forming: the isodensity H i structural parameters have stronger correlations with star formation. Normalising the H i disc size by the optical effective radius (instead of the isophotal radius) produces positive correlations with stellar masses and stellar surface densities and removes the correlations with star formation. This is due to the effective and isodensity H i radii increasing with mass at similar rates while, in the optical, the effective radius increases slower than the isophotal radius. Our results are in qualitative agreement with previous studies and demonstrate that with WALLABY we can begin to bridge the gap between small galaxy samples with high spatial resolution H i data and large, statistical studies using spatially unresolved, single-dish data.
$>$2 beams. We find that galaxies with higher H i surface densities and more extended H i discs tend to be more star forming: the isodensity H i structural parameters have stronger correlations with star formation. Normalising the H i disc size by the optical effective radius (instead of the isophotal radius) produces positive correlations with stellar masses and stellar surface densities and removes the correlations with star formation. This is due to the effective and isodensity H i radii increasing with mass at similar rates while, in the optical, the effective radius increases slower than the isophotal radius. Our results are in qualitative agreement with previous studies and demonstrate that with WALLABY we can begin to bridge the gap between small galaxy samples with high spatial resolution H i data and large, statistical studies using spatially unresolved, single-dish data.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of the Astronomical Society of Australia
References
- 2
- Cited by



