1 INTRODUCTION
The spectral classification of a star, along with its luminosity class, tells us about its surface temperature, colour, luminosity, and chemical and physical properties. For example, the MK spectral class of star Betelgeuse is M2Iab, where the first two characters indicate that it is a red star with effective temperature about 3 500 K, and the last three characters indicate that it is an intermediate luminous supergiant. Thus, knowledge of the correct spectral classification is essential to interpret various features of a star and also in the study of the evolution of our Galaxy as a whole. Various catalogues and databases give information about the spectral classification of the stars along with other astronomical data. One of the most widely used star catalogues is Hipparcos catalogue, which contains astronomical data of 118 218 stars with high precision astrometric positions. The stars observed in Hipparcos mission (launched by the European Space Agency (ESA) in 1989) were listed in the form of a catalogue (ESA Reference Perryman1997; Perryman et al. Reference Perryman1997), and MK spectral classifications (Morgan, Abt, & Tapscott Reference Morgan, Abt and Tapscott1978, Keenan, & McNeil Reference Keenan and McNeil1976) of the stars included in the Hipparcos catalogue were taken from a number of ground-based compilations referenced in the catalogue. Unfortunately, many of the stars in the main Hipparcos catalogue have been wrongly spectrally classified and these have been corrected periodically (e.g., Tsvetkov, Popov, & Smirnov Reference Tsvetkov, Popov and Smirnov2008; Montes et al. Reference Montes, Lopez-Santiago, Galvez, Fernandez-Figueroa, De Castro and Cornide2001; Torres et al. Reference Torres, Quast, da Silva, de la Reza, Melo and Sterzik2006, etc.), and therefore existing spectral classifications in the Hipparcos catalogue, which are also currently accepted in SIMBAD and other stellar databases, need to be checked for their correctness.
It is quite time-consuming to conduct an extensive survey on the spectrum of all the individual stars and reclassify them if they're found to be wrong. Hence, it is essential to obtain a first-hand collection of stars which have doubtful spectral classification. One simple method to find a collection of doubtful stars can be to compare the absolute magnitude of the stars as obtained from the observed data with their corresponding spectroscopic values (we can predict absolute magnitudes from precise spectral classification). Both values should agree with each other within a range of difference ±2 mag. If this difference is found to be unexpectedly large, this can be either due to wrong calibration of the spectroscopic magnitudes or wrong spectral classification of stars, or due to inaccurate astrometric data. If we use the Hipparcos catalogue––which gives high precision distance measurement data and observed V magnitudes–the last case is less likely to occur. The first possibility (wrong calibration of spectroscopic magnitudes) can also be ruled out if we get correct predictions for other stars of the same spectral class. So, the only reason for such large deviation should be the star's incorrect spectral classification.
In our present work, we have used data from the original Hipparcos catalogue to determine the absolute V magnitude of the stars within a distance of 100 pc from the Sun and compared these results with the absolute magnitude derived from the star's spectral class (i.e., calibrated absolute magnitudes, further discussed in Section 3). We found, as expected, that the two magnitudes are in agreement with each other within the error limits for most of the stars. We have identified those stars with significant deviations between the spectroscopic and Hipparcos magnitudes and ascribed them to doubtful spectral classification (Table 2). These stars have been checked in SIMBAD for their currently accepted classifications. Some of these have already been reported and corrected in the literature by other authors, and these now show much less deviation in absolute magnitude from the spectroscopic value with the new spectral class (Table 2). The rest of the stars from Table 2 should be restudied as these are most likely to have incorrect spectral classes.
Table 1. Data accessed from Hipparcos digital catalogue.

Table 2. Data for stars with significant difference between observed and spectroscopic absolute magnitudes.

aIn the above table, second column indicates the MK classification of stars according to Hipparcos catalogue, whereas 8th column indicates the modified MK class obtained from SIMBAD. Here M′V0 is the standard absolute V magnitude of modified MK class (Please see text for the meaning of other terms).
References. (1) Torres et al. Reference Torres, Quast, da Silva, de la Reza, Melo and Sterzik2006; (2) Tsvetkov et al. Reference Tsvetkov, Popov and Smirnov2008; (3) Jenkins et al. Reference Jenkins, Ramsey, Jones, Pavlenko, Gallardo, Barnes and Pinfield2009; (4) Gray et al. Reference Gray, Corbally, Garrison, McFadden, Bubar, McGahee, O’Donoghue and Knox2006; (5) Fulbright (Reference Fulbright2000); (6) Montes et al. Reference Montes, Lopez-Santiago, Galvez, Fernandez-Figueroa, De Castro and Cornide2001; (7) Westerlund, Olander & Hedin Reference Westerlund, Olander and Hedin1981; (8) Koen et al. Reference Koen, Kilkenny, Van Wyk and Marang2010; (9) Naze (Reference Naze2009), (10) Abt (Reference Abt2009), (11) luminosity class of the star was not provided. The luminosity class III was selected so that the deviation (MV – M′V0 ) is minimised (present work).
2 BACKGROUND AND THEORY
2.1. Introducing Hipparcos catalogue
The Hipparcos catalogue (http://www.rssd.esa.int/Hipparcos/catalog.html) has been a very useful database for astronomers to analyse various astrophysical properties of the stars in our Milky Way. A more accurate version of Hipparcos data has also been proposed recently (van Leeuwen Reference van Leeuwen2007). Some recent works involving the Hipparcos catalogue include those by Rhee et al. (Reference Rhee, Song, Zuckerman and McElwain2007), Melendez et al. (Reference Melendez, Asplund, Gustafsson and Yong2009), Welsh et al. (Reference Welsh, Lallement, Vergely and Raimond2010), etc.
In the Hipparcos catalogue there are a total of 77 distinct columns denoted by H1, H2, H3, etc., some of which we use in the columns tabulated in Table 1, introducing the fields accessed from the Hipparcos digital catalogue.
Other relevant information regarding these columns about double star data in the Hipparcos catalogue were obtained from Lindegren et al. (Reference Lindegren1997) and photometric data from van Leeuwen et al. (Reference van Leeuwen, Evans, Grenon, Grossmann, Mignard and Perryman1997).
2.2. Theory
The absolute V magnitude (MV ) of a star is given by the relation:
where mV denotes the apparent V magnitude, d is the distance of the star in parsec, and AV is the extinction correction due to interstellar material.
As stated above, mV can be read directly from field H5 of the Hipparcos catalogue and the distance d (in pc) can be calculated from trigonometric parallax (in arcsec) from the relation (e.g., Zeilik & Gregory Reference Zeilik and Gregory1998):
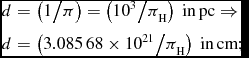 \begin{eqnarray}
d &=& ( {{1 / \pi }} ) = ( {{{10^3 } / {\pi _{\rm H} }}} )\;{\rm in}\,{\rm pc} \Rightarrow\nonumber\\
d &=& ( {{{3.085\,68 \times 10^{21} } / {\pi _{\rm H} }}} )\;{\rm in}\,{\rm cm;}\end{eqnarray}
\begin{eqnarray}
d &=& ( {{1 / \pi }} ) = ( {{{10^3 } / {\pi _{\rm H} }}} )\;{\rm in}\,{\rm pc} \Rightarrow\nonumber\\
d &=& ( {{{3.085\,68 \times 10^{21} } / {\pi _{\rm H} }}} )\;{\rm in}\,{\rm cm;}\end{eqnarray}
where π is the parallax in arcsec and π H is the parallax in milliarcsec as given in Hipparcos catalogue (Table 1: H11).
The extinction AV can be estimated from the column density of hydrogen by using the relationship (Guver & Ozel Reference Guver and Ozel2009):
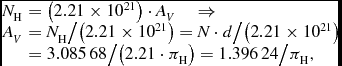 \begin{equation}
\begin{array}{rl}
N_{\rm H} & = ( {2.21 \times 10^{21} } ) \cdot A_V \quad \Rightarrow \\
A_V & = {{N_{\rm H} } / {( {2.21 \times 10^{21} } ) = \ }}{{N \cdot d} / {( {2.21 \times 10^{21} } )}}\\
& = {{3.085\,68} / {( {2.21 \cdot \pi _{\rm H} } )}} = {{1.396\,24} / {\pi _{\rm H} }}, \\
\end{array}\end{equation}
\begin{equation}
\begin{array}{rl}
N_{\rm H} & = ( {2.21 \times 10^{21} } ) \cdot A_V \quad \Rightarrow \\
A_V & = {{N_{\rm H} } / {( {2.21 \times 10^{21} } ) = \ }}{{N \cdot d} / {( {2.21 \times 10^{21} } )}}\\
& = {{3.085\,68} / {( {2.21 \cdot \pi _{\rm H} } )}} = {{1.396\,24} / {\pi _{\rm H} }}, \\
\end{array}\end{equation}
where N H = N.d is the column density of hydrogen along the direction of the star and N is the average number of hydrogen atom, molecule or ion per cm3 along the direction of the star of distance d expressed in cm. The value of N within 100 pc along various directions of the sky is less than 1 cm−3 (Cash, Bowyer, & Lampton Reference Cash, Bowyer and Lampton1979). In the calculation of column density of hydrogen N H, we put N = 1 cm−3 so that a maximum value of AV can be obtained from Equation (3). Replacing Equations (2) and (3) in Equation (1), we have the following:
Thus, knowing mV and πH, the absolute V magnitude MV of a star can be calculated by using the above relation.
2.3. Error estimation
To estimate the maximum possible error in determining MV from Equations (1) and (4), which may come across due to the lack of accurate knowledge of mV and d, we can take the differential of Equations (1) and (4) which leads to
In order to get maximum possible error in MV we should use only positive values of the errors because otherwise they may cancel each other, reducing the error limit.
3 METHODOLOGY
3.1. Determination of MV0 values for spectral classes
For each luminosity class, there is a close correlation between spectral types with the absolute magnitude of stars (Allen & Cox Reference Allen and Cox2000). MV0 refers to the absolute magnitude, which is considered as standard for a given MK class. These values were collected directly from various sources described below. Wherever a direct match was not found, interpolation was applied. In a few remaining cases absolute magnitudes of the nearby stars of confidently known spectral class were considered to be standard for that spectral class.
The method of assigning MV0 values to the MK classes from the Hipparcos catalogue (given at the field H76) is as follows––at the first step, a comprehensive list of the 3 838 different and unique spectral types along with different luminosity classes, mentioned in the column H76 of the Hipparcos data, was collected. This list was subdivided into separate luminosity classes. Wherever luminosity class was not explicitly mentioned, we assumed it as a part of the main sequence V stars. Now, Allen & Cox (Reference Allen and Cox2000) in their Table 15.7 have provided a calibration of MK spectral types of different luminosity class (main sequence V, giants III and super giants I) with absolute V magnitudes and other quantities such as colour, T eff and BC. Again, Table 19.1 of Allen & Cox (Reference Allen and Cox2000) lists the 100 nearest stars to the Earth in order of increasing distance.Footnote 1 From this table we obtain the relation between MK spectral types and luminosity class of the 100 nearest stars with MV0 , which was used to interpolate MV0 for those luminosity classes that were absent in Table 15.7 of Allen & Cox (Reference Allen and Cox2000). Using the above information and additional data that we obtained from Lang (Reference Lang1982), Zombeck (Reference Zombeck1990), and SIMBAD (http://simbad.u-strasbg.fr/simbad/), an association table matching absolute magnitudes (MV0 ) with MK spectral type, along with luminosity classes, was collected. This table was matched with the list of 3 838 unique MK spectral types in the Hipparcos data, and MV0 were associated with each matching MK Spectral Type.
It is important to state that the maximum magnitude variation is due to (i) the luminosity class (I, II, III, V, etc.), (ii) spectral type alphabets (O, B, A, F, G, K, M), and (iii) the number following these alphabets (0, 1,. . .,9). Other details in the spectral type were noticed to have small variations which hardly contributed in the absolute magnitude variations. The 3 838 unique MK spectral types in the Hipparcos data were first sorted as per luminosity class. Then each luminosity class was sorted as per the spectral type alphabet in the following order of (O, B, A, F, G, K, M). Each of these subsets was sorted by the number following these alphabets (0, 1,. . .,9).
As told above, in the list of 3 838 unique MK spectral types in the Hipparcos data, where we could not find a direct match of the spectral type from the above literatures, we interpolated within a particular luminosity class to associate a MV0 to that star to fill in the gaps. The interpolation variations in MV0 have been less than 1 mag. This created database also contains KURUCZ Flux Files (Colina Reference Colina1995) associated with these spectral types. This table along with this information, though not relevant to this work, was earlier used by one of the authors during the research work presented in the paper by Sujatha et al. (Reference Sujatha, Chakraborty, Murthy and Henry2004).
3.2. Comparison of MV0 with MV values
A fortran program was written to extract all the necessary data (Table 1) from the Hipparcos catalogue. Only those stars which are within 100 pc of the Sun were used because of the errors associated with smaller values of the parallax. This data was tabulated in a list (List-1). Since it would take the as yet undiscovered Population III stars to approach a deviation in |MV – MV0 | of 5 mag or more, low metallicity in stars was not taken into account. The distance d, the extinction AV , the absolute V magnitude MV and maximum error in the absolute V magnitude for all the stars in List-1 were calculated from Equations (2)–(5), respectively, and appended to List-1. We then associated MV0 values corresponding to the spectral class of each star from List-1 and added into it.
In Figure 1(a), we plot MV versus MV0 from List-1 for stars with a distance closer or equal to 100 pc. In Figure 1(b), the difference (MV – MV0 ) is plotted against MV . In Figure 1(c), we again plot the difference (MV – MV0 ), this time with respect to spectral type (O, B, A, F, G, K, M) and irrespective of the luminosity class. No special trend is observed which reflects any biasness with respect to distance or spectral type. In Figure 2, we can see how the stars are distributed from the line of zero difference, and Figure 3 shows the distance dependence of MV –MV0 of the stars from List-1.

Figure 1. (a) A plot between Hipparcos and spectroscopic absolute magnitude (MV and MV0 ) of the stars from Hipparcos catalogue which are nearer than or equal to 100 pc of distance. (b) In this figure, (MV – MV0 ) has been plotted against MV . No special trend is observed. (c) In this figure, MV and MV0 have been compared while breaking down the comparison according to the spectral type range. The spectral code (XY) indicates a spectral classification as follows: X = 0,1,2,3,4,5,6 for spectral classes O, B, A, F, G, K, M respectively and the value of Y = 0,1,2,. . .,9 indicates their sub-classification. Circles indicate those stars which have been assigned a sub-classification (0,1,2, etc.) in Hipparcos catalogue, whereas crosses indicate the few stars which were not assigned any sub-class (such as O,. . ., M:, Am, etc.) plotted at the position X5.

Figure 2. Logarithmic frequency distribution of MV – MV0 . This figure shows that most of the stars are in agreement with their standard result, but a few stars show abnormal deviation.

Figure 3. A plot between distance of the stars in parsec and MV – MV0 . It clearly shows that unexpected deviations have no systematic dependence with the distance. Gradually diverging black region along the zero difference line is due to interstellar extinction.
4 ANALYSIS
We separate out those stars with MV – MV0 greater than the expected maximum error for that star calculated from Equation (5) (shown in Figure 4). It is evident from ESA (Reference Perryman1997) that the experimental error in V magnitude is ~10−2. To assign a maximum error limit in mV we put mV = 1 in Equation (5). The maximum and minimum of the Hipparcos magnitude H p of variable stars were obtained from H49 and H50 respectively. Variable stars which have a maximum variation in H p more than 1 mag (|H49–H50| > 1) and the multiple star systems have also been rejected from List-1. To calculate the maximum error in parallax part of Equation (5), we put δπ = 1.5σπ so that a maximum ± error assigned to δπ be 3σπ (obtained from H16). Thus in a final list we get a total of 2 853 stars out of the 21 595 stars of List-1 which significantly deviate from the standard photometric behaviour. These stars are plotted in Figure 4 to show the deviation of (MV – MV0 ) versus distance dependence.

Figure 4. Same as Figure 3 but shows only those stars with errors more than ±δMV .
We find that 2 853 number of stars of List-1 show a greater value of (MV – MV0 ) than greatest possible error in MV . This is because of the fact that MV0 values that have been used here are just average values that have been considered to be standard for a given spectral class. However in reality, the absolute magnitude may vary within a given range from the standard value which introduces an additional deviation which was not included in δMV . In any case, if the absolute value of the deviation (i.e., |MV –MV0 |) is equal to 5 mag or more, it is large enough to say that the error is abnormal, because, it can be easily realised from H–R diagram that addition or subtraction of 5 mag in MV of a star must change its spectral class, whereas error in MV0 cannot be so high which is evident from correct match between MV and MV0 for about 87% of the stars (Figures 1(a), 2, and 3). Therefore, the stars with abnormal deviation must have been wrongly spectrally classified, or the extinction of the interstellar medium is very different from the calculated AV in which we have assumed a constant N = 1 cm−3 (Cash et al. Reference Cash, Bowyer and Lampton1979).
Those stars from the 2 853 stars which show a difference in absolute magnitude greater or equal to 5 mag (|MV – MV0 | ≥ 5) are separated out and compiled in Table 2. We then check their classification in the SIMBAD database. We found that some of these stars have already been corrected for spectral classification and show much lower difference with the new spectral class. The absolute magnitude derived for this new spectral classification is shown as M′V0 in the 9th column and (|MV – M′V0 |) in the 10th column of Table 2. The new spectral classification and the reference number of these changes in spectral type are in the 8th and 11th column respectively. The relevant citations corresponding to these numbers are mentioned below in the Table 2. The remaining stars for which we did not find any record of correction in MK spectral classification are marked as ‘unchanged’ in the 8th column in Table 2.
For the stars that still show a deviation of |MV – MV0 |≥ 5 or |MV – M′V0 | ≥5, we need to verify if it is a result due to variation in interstellar extinction. We therefore plot the position of these stars in galactic co-ordinates in an Aitoff projection shown in Figure 5. The stars with d < 50 pc have been plotted with triangular points while the stars between 50 pc ≤ d < 100 pc have been plotted with circular points. We notice that these stars are distributed all across the galactic sky. We now over-plotted these positions over integrated opacity derived by Vergely et al. (Reference Vergely, Valette, Lallement and Raimond2010) (Figure 6) for a line of sight distance of 250 pc so that it can be understood if they belong to any dark region of our Galaxy which may introduce an abnormal extinction in magnitude. From Figure 6, we see that the position of the stars does not correlate with the high opacity region. It is true that some of the stars are in the bordering region of high opacity. In Equation (1), interstellar extinction is taken care with AV = N.d/(2.21 × 1021). We tried to change N so that (MV – MV0 ) reduces below 5. The values of N thus obtained seem extremely unrealistic. The star HIP64871, which is at a high galactic latitude, where we expect low interstellar extinction, needs to have N = 2 cm−3 to bring the deviation in (MV – MV0 ) below 5. For the stars HIP87083, HIP87092, and HIP87345 which are towards the galactic centre, the value of N required is 3 cm−3, 10 cm−3, and 45 cm−3, respectively. These numbers are totally unrealistic. It is therefore clear that the reason for abnormality in magnitudes is not due to any abnormal extinction. It is most probably due to incorrect MK classification of these stars which is in use presently (misidentification of stars can be a very likely reason for such wrong classifications).

Figure 5. This figure shows the position of the stars with |MV – MV0 | ≥ 5 mag. (Table 2) in our Galaxy. It is clear from this figure that the stars are well scattered throughout the galactic sphere and do not belong to any particular dark region.

Figure 6. The stars from Figure 5 are over-plotted on integrated opacity derived by Vergely et al. (Reference Vergely, Valette, Lallement and Raimond2010) for a line of site distance of 250 pc. The plot is in galactic co-ordinates in Aitoff projection. The positions of the stars do not show any correlation with the high opacity regions. Credit: Vergely J.-L., Valette B., Lallement R. & Raimond S., A&A, 518, A31, 2010, reproduced with permission © ESO.
Since a complete MK spectral classification (i.e., spectral type and luminosity) is a morphological description of the spectrum, it is independent of Hipparcos distances. However, it does often correlate with them (Garrison Reference Garrison2002). Therefore some luminosity classes, such as those arising from high microturbulence in the F-type stars, may not be wrong. However, the differences from microturbulence are within the ±2 mag, which is well within the working limit of this work.
5 CONCLUSION
We have listed all those stars in Table 2 which deviate abnormally from their standard photometric behaviour. With new corrected spectral class (obtained from SIMBAD), they show much lower deviation in absolute V magnitude (MV – M′V0 ), which indicates correctness of their present classification. HIP 23 475 has been classified in the Hipparcos as K3. The luminosity class has not been defined. This gave a high deviation in (MV – MV0 ). Adjusting the luminosity class to III drastically reduced the deviation in (MV – M′V0 ). The other stars in Table 2, where the luminosity class has not been explicitly defined and have high deviation in (MV – MV0 ), are HIP46299 (M2), HIP14777 (B2), HIP40430 (B + . . . modified to O9nne), and HIP21000 (F8 + . . . modified to F8). In these cases choice of luminosity other than V does not reduce the deviation.
From Table 2 we see that majority of these doubtful stars are late type stars, while Figure 1(c) shows a fairly uniform distribution with respect to spectral class. It is possible that late type stars are less carefully studied, as it is of less interest whether they belong to K class or M class, and hence were misclassified. But it should be noted that there are stars (like HIP15973, HIP23342, HIP43177, etc.) in this list whose spectral classifications have been noticeably changed after correction, and they give much less deviation in absolute magnitude with the new spectral class. There are three stars (HIP40430, HIP21000, and HIP46360) that have still shown significant deviation after correction of spectral class. These stars along with the rest of the stars from Table 2, where spectral class has not been corrected (marked as ‘unchanged’), must be re-studied carefully for correct classification. There is no other reason which accounts for such an abnormal high deviation in (MV – MV0 ), if the other Hipparcos data (such as V magnitude, parallax, etc.) are believed to be correct for the star. There is great possibility that they bear wrong spectral and/or luminosity class.
We do not claim that the list of wrongly classified stars shown in Table 2 is exhaustive. There may be several other stars that exist for which |MV – MV0 | value is less than 5, but spectral classification is incorrect.
ACKNOWLEDGEMENTS
D. Deb is thankful to Subrato Bhattacharjee of Assam University, Silchar, for his moral help during this work. P. Chakraborty thanks Prof. Jayant Murthy of Indian Institute of Astrophysics, Bangalore, India, for his comments and suggestions in preparing this manuscript. This work has extensively made use of the Hipparcos and the SIMBAD database. SIMBAD database is operated at CDS, Strasbourg, France. We are thankful to this database without which this work could not have been possible. Finally, we acknowledge comments from the referees of this paper which have improved its quality to a good extent.
APPENDIX-A
We have compared the spectral classes from Table 19.1 of Allen and Cox (Reference Allen and Cox2000) with that obtained from SIMBAD. There are 114 stars which were common and comparable for spectral classes.

Figure A.1. A comparison between MK classes from Table 19.1 (Allen and Cox Reference Allen and Cox2000) and recent SIMBAD results for the same set of stars. (a) Spectral classes have been compared by taking ratio between spectral code (XY, as described in Figure 1(c)) ratios due to SIMBAD and Table 19.1 of Allen and Cox (Reference Allen and Cox2000). (b) A corresponding plot for luminosity classes. Luminosity classes - I, II, III, IV and V have been coded by assigning numbers 1, 2, 3, 4 and 5, respectively. Other details have been neglected.












