1 INTRODUCTION
The explosions of massive stars as core-collapse supernovae (CCSNe) constitute one of the most outstanding problems in modern astrophysics. This is in no small measure due to the critical role of supernova explosions in the history of the Universe. CCSNe figure prominently in the chemical evolution of galaxies as the dominant producers, e.g., of elements between oxygen and the iron group (Arnett Reference Arnett1996; Woosley, Heger, & Weaver Reference Woosley, Heger and Weaver2002), and supernova feedback is a key ingredient in the modern theory of star formation (Krumholz Reference Krumholz2014). The properties of neutron stars and stellar-mass black holes (masses, spins, kicks; Özel et al. Reference Özel, Psaltis, Narayan and McClintock2010, Reference Özel, Psaltis, Narayan and Santos Villarreal2012; Kiziltan et al. Reference Kiziltan, Kottas, De Yoreo and Thorsett2013; Antoniadis et al. Reference Antoniadis, Tauris, Ozel, Barr, Champion and Freire2016; Arzoumanian, Chernoff, & Cordes Reference Arzoumanian, Chernoff and Cordes2002; Hobbs et al. Reference Hobbs, Lorimer, Lyne and Kramer2005) cannot be understood without addressing the origin of these compact objects in stellar explosions.
Why (some) massive stars explode is, however, a daunting problem in its own right regardless of the wider implications of supernova explosions: The connection of supernovae of massive stars with the gravitational collapse to a neutron star has been postulated more than 80 yr ago (Baade & Zwicky Reference Baade and Zwicky1934), and the best-explored mechanism for powering the explosion, the neutrino-driven mechanism, has gone through several stages of ‘moulting’ in the 50 yr after its conception by Colgate & White (Reference Colgate and White1966). Yet, the problem of the supernova explosion mechanism still awaits a definitive solution. The rugged path towards an understanding of the explosion mechanism merely reflects that CCSNe are the epitome of a ‘multi-physics’ problem that combines aspects of stellar structure and evolution, nuclear and neutrino physics, fluid dynamics, kinetic theory, and general relativity. We cannot recapitulate the history of the field here and instead refer the reader to the classical and modern reviews of Bethe (Reference Bethe1990), Arnett (Reference Arnett1996), Mezzacappa (Reference Mezzacappa2005), Kotake, Sato, & Takahashi (Reference Kotake, Sato and Takahashi2006), Janka et al. (Reference Janka, Langanke, Marek, Martínez-Pinedo and Müller2007), Burrows et al. (Reference Burrows, Livne, Dessart, Ott and Murphy2007a), Janka (Reference Janka2012), and Burrows (Reference Burrows2013) as starting points.
The longevity of the supernova problem should not be misinterpreted: Despite the occasional detour, supernova theory has made steady progress, particularly so during the last few years, which have seen the emergence of mature—and increasingly successful—multi-dimensional first-principle simulations of the collapse and explosion of massive stars as well as conceptual advances in our understanding of the neutrino-driven explosion mechanism and its interplay with multi-dimensional hydrodynamic instabilities.
1.1 The neutrino-driven explosion mechanism in its modern flavour
Before we review these recent advances, it is apposite to briefly recapitulate the basic idea of the neutrino-driven supernova mechanism in its modern guise. Stars with zero-age main sequence (ZAMS) masses above
![]() ${\gtrsim }8\,\text{M}_\odot$
and with a helium core mass
${\gtrsim }8\,\text{M}_\odot$
and with a helium core mass
![]() ${\lesssim }65\,\text{M}_\odot$
(the lower limit for non-pulsational pair-instability supernovae; Heger & Woosley Reference Heger and Woosley2002; Heger et al. Reference Heger, Fryer, Woosley, Langer and Hartmann2003) develop iron cores that eventually become subject to gravitational instability and undergo collapse on a free-fall timescale. For low-mass supernova progenitors with highly degenerate iron cores, collapse is triggered by the reduction of the electron degeneracy pressure due to electron captures; for more massive stars with higher core entropy and a strong contribution of radiation pressure, photo-disintegration of heavy nuclei also contributes to gravitational instability. Aside from these ‘iron-core supernovae’, there may also be a route towards core collapse from super-AGB stars with O–Ne–Mg cores (Nomoto Reference Nomoto1984, Reference Nomoto1987; Poelarends et al. Reference Poelarends, Herwig, Langer and Heger2008; Jones et al. Reference Jones2013; Jones, Hirschi, & Nomoto Reference Jones, Hirschi and Nomoto2014; Doherty et al. Reference Doherty, Gil-Pons, Siess, Lattanzio and Lau2015), where rapid core contraction is triggered by electron captures on 20Ne and 24Mg;Footnote
1
hence this sub-class is designated as ‘electron-capture supernovae’ (ECSNe).
${\lesssim }65\,\text{M}_\odot$
(the lower limit for non-pulsational pair-instability supernovae; Heger & Woosley Reference Heger and Woosley2002; Heger et al. Reference Heger, Fryer, Woosley, Langer and Hartmann2003) develop iron cores that eventually become subject to gravitational instability and undergo collapse on a free-fall timescale. For low-mass supernova progenitors with highly degenerate iron cores, collapse is triggered by the reduction of the electron degeneracy pressure due to electron captures; for more massive stars with higher core entropy and a strong contribution of radiation pressure, photo-disintegration of heavy nuclei also contributes to gravitational instability. Aside from these ‘iron-core supernovae’, there may also be a route towards core collapse from super-AGB stars with O–Ne–Mg cores (Nomoto Reference Nomoto1984, Reference Nomoto1987; Poelarends et al. Reference Poelarends, Herwig, Langer and Heger2008; Jones et al. Reference Jones2013; Jones, Hirschi, & Nomoto Reference Jones, Hirschi and Nomoto2014; Doherty et al. Reference Doherty, Gil-Pons, Siess, Lattanzio and Lau2015), where rapid core contraction is triggered by electron captures on 20Ne and 24Mg;Footnote
1
hence this sub-class is designated as ‘electron-capture supernovae’ (ECSNe).
According to modern shell-model calculations (Langanke & Martínez-Pinedo Reference Langanke and Martínez-Pinedo2000; Langanke et al. Reference Langanke2003), the electron capture rate on heavy nuclei remains high even during the advanced stages of collapse (Langanke et al. Reference Langanke2003) when the composition of the core is dominated by increasingly neutron-rich and massive nuclei. Further deleptonisation during collapse thus reduces the lepton fraction Y
lep to about 0.3 according to modern simulations (Marek et al. Reference Marek, Janka, Buras, Liebendörfer and Rampp2005; Sullivan et al. Reference Sullivan, O’Connor, Zegers and Grubb2016) until neutrino trapping occurs at a density of
![]() $\mathord {\sim }10^{12} \, {\rm g} \, {\rm cm}^{-3}$
. As a result, the homologously collapsing inner core shrinks (Yahil Reference Yahil1983), and the shock forms at a small enclosed mass of
$\mathord {\sim }10^{12} \, {\rm g} \, {\rm cm}^{-3}$
. As a result, the homologously collapsing inner core shrinks (Yahil Reference Yahil1983), and the shock forms at a small enclosed mass of
![]() $\mathord {\sim } 0.5\,\text{M}_\odot$
(Langanke et al. Reference Langanke2003; Hix et al. Reference Hix, Messer, Mezzacappa, Liebendörfer, Sampaio, Langanke, Dean and Martínez-Pinedo2003; Marek et al. Reference Marek, Janka, Buras, Liebendörfer and Rampp2005) after the core reaches supranuclear densities and rebounds (bounces). Due to photodisintegration of heavy nuclei in the infalling shells into free nucleons as well as rapid deleptonisation in the post-shock region once the shock breaks out of the neutrinosphere, the shock stalls a few milliseconds after bounce, i.e., it turns into an accretion shock with negative radial velocity downstream of the shock. Aided by a continuous reduction of the mass accretion rate onto the young proto-neutron star, the stalled accretion shock still propagates outward for
$\mathord {\sim } 0.5\,\text{M}_\odot$
(Langanke et al. Reference Langanke2003; Hix et al. Reference Hix, Messer, Mezzacappa, Liebendörfer, Sampaio, Langanke, Dean and Martínez-Pinedo2003; Marek et al. Reference Marek, Janka, Buras, Liebendörfer and Rampp2005) after the core reaches supranuclear densities and rebounds (bounces). Due to photodisintegration of heavy nuclei in the infalling shells into free nucleons as well as rapid deleptonisation in the post-shock region once the shock breaks out of the neutrinosphere, the shock stalls a few milliseconds after bounce, i.e., it turns into an accretion shock with negative radial velocity downstream of the shock. Aided by a continuous reduction of the mass accretion rate onto the young proto-neutron star, the stalled accretion shock still propagates outward for
![]() $\mathord {\sim } 70 \, {\rm ms}$
, however, and reaches a typical peak radius of
$\mathord {\sim } 70 \, {\rm ms}$
, however, and reaches a typical peak radius of
![]() $\mathord {\sim } 150 \, {\rm km}$
before it starts to recede again.
$\mathord {\sim } 150 \, {\rm km}$
before it starts to recede again.
The point of maximum shock expansion is roughly coincident with several other important changes in the post-shock region: Photons and electron–positron pairs become the dominant source of pressure in the immediate post-shock region, deleptonisation behind the shock occurs more gradually, and the electron neutrino and anti-neutrino luminosities become similar. Most notably, a region of net neutrino heating (gain region) emerges behind the shock. In the ‘delayed neutrino-driven mechanism’ as conceived by Bethe & Wilson (Reference Bethe and Wilson1985) and Wilson (Reference Wilson, Centrella, Leblanc and Bowers1985), the neutrino heating eventually leads to a sufficient increase of the post-shock pressure to ‘revive’ the shock and make it re-expand, although the post-shock velocity initially remains negative. Since shock expansion increases the mass of the dissociated material exposed to strong neutrino heating, this is thought to be a self-sustaining runaway process that eventually pumps sufficient energy into the post-shock region to allow for the development of positive post-shock velocities and, further down the road, the expulsion of the stellar envelope.
Modern simulations of CCSNe that include energy-dependent neutrino transport, state-of-the art microphysics, and (to various degrees) general relativistic effects have demonstrated that the neutrino-driven mechanism is not viable in spherical symmetry (Rampp & Janka Reference Rampp and Janka2000, Reference Rampp and Janka2002; Liebendörfer et al. Reference Liebendörfer, Mezzacappa, Thielemann, Messer, Hix and Bruenn2001, Reference Liebendörfer, Messer, Mezzacappa, Bruenn, Cardall and Thielemann2004, Reference Liebendörfer, Rampp, Janka and Mezzacappa2005; Sumiyoshi et al. Reference Sumiyoshi, Yamada, Suzuki, Shen and Chiba2005; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a, Reference Buras, Janka, Rampp and Kifonidis2006b; Müller, Janka, & Dimmelmeier Reference Müller, Janka and Dimmelmeier2010; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010; Lentz et al. Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012a, Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012b), except for supernova progenitors of the lowest masses (Kitaura, Janka, & Hillebrandt Reference Kitaura, Janka and Hillebrandt2006; Janka et al. Reference Janka, Müller, Kitaura and Buras2008; Burrows, Dessart, & Livne Reference Burrows, Dessart, Livne, Immler, Weiler and McCray2007b; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010), which will be discussed in Section 2.
In its modern guise, the paradigm of neutrino-driven explosions therefore relies on the joint action of neutrino heating and various hydrodynamic instabilities to achieve shock revival. As demonstrated by the first generation of multi-dimensional supernova models in the 1990s (Herant et al. Reference Herant, Benz, Hix, Fryer and Colgate1994; Burrows, Hayes, & Fryxell Reference Burrows, Hayes and Fryxell1995; Janka & Müller Reference Janka and Müller1995, Reference Janka and Müller1996), the gain region is subject to convective instability due to the negative entropy gradient established by neutrino heating. Convection can be suppressed if the accreted material is quickly advected from the shock to the gain radius (Foglizzo, Scheck, & Janka Reference Foglizzo, Scheck and Janka2006). Under these conditions, the standing accretion shock instability (SASI; Blondin, Mezzacappa, & DeMarino Reference Blondin, Mezzacappa and DeMarino2003; Blondin & Mezzacappa Reference Blondin and Mezzacappa2006; Foglizzo et al. Reference Foglizzo, Galletti, Scheck and Janka2007; Laming Reference Laming2007; Yamasaki & Yamada Reference Yamasaki and Yamada2007; Fernández & Thompson Reference Fernández and Thompson2009a, Reference Fernández and Thompson2009b) can still grow, which is mediated by an advective-acoustic cycle (Foglizzo Reference Foglizzo2002; Foglizzo et al. Reference Foglizzo, Galletti, Scheck and Janka2007; Guilet & Foglizzo Reference Guilet and Foglizzo2012) and manifests itself in the form of large-scale sloshing and spiral motions of the shock. The precise mechanism whereby these instabilities aid shock revival requires careful discussion (see Section 3.3), but their net effect can be quantified using the concept of the ‘critical luminosity’ (Burrows & Goshy Reference Burrows and Goshy1993) for the transition from a steady-state accretion flow to runaway shock expansion: In effect, convection and/or the SASI reduce the critical luminosity in multi-D by 20. . .30% (Murphy & Burrows Reference Murphy and Burrows2008; Nordhaus et al. Reference Nordhaus, Burrows, Almgren and Bell2010; Hanke et al. Reference Hanke, Marek, Müller and Janka2012; Fernández Reference Fernández2015) compared to the case of spherical symmetry (1D).
1.2 Current questions and structure of this review
We cannot hope to comprehensively review all aspects of the CCSN explosion problem, even if we limit ourselves to the neutrino-driven paradigm. Instead we shall focus on the following topics that immediately connect to the above overview of the neutrino-driven mechanism:
-
• The neutrino-driven explosion mechanism demonstrably works at the low-mass end of supernova progenitors. In Section 2, we shall discuss the specific explosion dynamics in the region around the mass limit for iron-core formation, i.e., for ECSN progenitors and structurally similar iron-core progenitors. We shall also consider the nucleosynthesis in these explosions; since they are robust, occur early after bounce, and can easily be simulated until the explosion energy has saturated, explosions of ECSN and ECSN-like progenitors currently offer the best opportunity to study CCSN nucleosynthesis based on first-principle explosion models.
-
• For more massive progenitors, it has yet to be demonstrated that the neutrino-driven mechanism can produce robust explosions in 3D with explosion properties (e.g., explosion energy, nickel mass, remnant mass) that are compatible with observations. In Section 3, we shall review the current status of 3D supernova simulations, highlighting the successes and problems of the current generation of models and detailing the recent progress towards a quantitative understanding of the interplay of neutrino heating and multi-dimensional fluid flow.
-
• In the wake of a rapid expansion of the field of CCSN modelling, a wide variety of methods have been employed to investigate the supernova problem with a continuum from a rigorous first-principle approach to parameterised models of limited applicability that are only suitable for attacking well-circumscribed problems. In Section 4, we present an overview of the different numerical approaches to simulations of neutrino-driven explosions and provide some guidance for assessing and comparing simulation results.
-
• The problem of shock revival by the neutrino-driven mechanism has not been conclusively solved. In Section 5, we shall review one of the promising ideas that could help explain supernova explosions over a wide range of progenitors, viz. the suggestion that shock revival may be facilitated by strong seed perturbations from prior convective shell burning in the infalling O or Si shells (Arnett & Meakin Reference Arnett and Meakin2011; Couch & Ott Reference Couch and Ott2013; Müller & Janka Reference Müller and Janka2015; Couch et al. Reference Couch, Chatzopoulos, Arnett and Timmes2015; Müller et al. Reference Müller, Viallet, Heger and Janka2016a); and we shall also discuss some other perspectives opened up by current and future 3D simulations of late burning stages in supernova progenitors.
Potential observational probes for multi-dimensional fluid flow in the supernova core during the first
![]() $\mathord {\sim } 1 \, {\rm s}$
exist in the form of the neutrino and gravitational wave signals, but we shall not touch these in any depth and instead point the reader to topical reviews (Ott Reference Ott2009 and Kotake Reference Kotake2013 for gravitational wave emission; Mirizzi et al. Reference Mirizzi, Tamborra, Janka, Saviano, Scholberg, Bollig, Hüdepohl and Chakraborty2016 for the neutrino signal) as well as some of the major publications of recent years (gravitational waves: Müller, Janka, & Marek Reference Müller, Janka and Marek2013; Yakunin et al. Reference Yakunin2015; Nakamura et al. Reference Nakamura, Horiuchi, Tanaka, Hayama, Takiwaki and Kotake2016; neutrinos: Tamborra et al. Reference Tamborra, Hanke, Müller, Janka and Raffelt2013, Reference Tamborra, Raffelt, Hanke, Janka and Müller2014a; Müller & Janka Reference Müller and Janka2014). Neither do we address alternative explosion scenarios here and refer the reader to Janka (Reference Janka2012) for a broader discussion that covers, e.g., the magnetorotational mechanism as the most likely explanation for hypernovae with explosion energies of up to
$\mathord {\sim } 1 \, {\rm s}$
exist in the form of the neutrino and gravitational wave signals, but we shall not touch these in any depth and instead point the reader to topical reviews (Ott Reference Ott2009 and Kotake Reference Kotake2013 for gravitational wave emission; Mirizzi et al. Reference Mirizzi, Tamborra, Janka, Saviano, Scholberg, Bollig, Hüdepohl and Chakraborty2016 for the neutrino signal) as well as some of the major publications of recent years (gravitational waves: Müller, Janka, & Marek Reference Müller, Janka and Marek2013; Yakunin et al. Reference Yakunin2015; Nakamura et al. Reference Nakamura, Horiuchi, Tanaka, Hayama, Takiwaki and Kotake2016; neutrinos: Tamborra et al. Reference Tamborra, Hanke, Müller, Janka and Raffelt2013, Reference Tamborra, Raffelt, Hanke, Janka and Müller2014a; Müller & Janka Reference Müller and Janka2014). Neither do we address alternative explosion scenarios here and refer the reader to Janka (Reference Janka2012) for a broader discussion that covers, e.g., the magnetorotational mechanism as the most likely explanation for hypernovae with explosion energies of up to
![]() $\mathord {\sim } 10^{52} \, {\rm erg}$
.
$\mathord {\sim } 10^{52} \, {\rm erg}$
.
2 THE LOW-MASS END ELECTRON-CAPTURE SUPERNOVAE AND THEIR COUSINS
Stars with ZAMS masses in the range
![]() $\mathord {\sim } 8 \ldots 10\,\text{M}_\odot$
exhibit structural peculiarities during their evolution that considerably affect the supernova explosion dynamics if they undergo core-collapse. The classical path towards ECSNe (Nomoto Reference Nomoto1984, Reference Nomoto1987), where electron captures on 24Mg and 20Ne in a degenerate O–Ne–Mg core of
$\mathord {\sim } 8 \ldots 10\,\text{M}_\odot$
exhibit structural peculiarities during their evolution that considerably affect the supernova explosion dynamics if they undergo core-collapse. The classical path towards ECSNe (Nomoto Reference Nomoto1984, Reference Nomoto1987), where electron captures on 24Mg and 20Ne in a degenerate O–Ne–Mg core of
![]() $\mathord {{\sim }1.37}\,\text{M}_\odot$
drive the core towards collapse, best exemplifies these peculiarities: Only a small C/O layer is present on top of the core, and the He layer has been effectively whittled down by dredge-up. The consequence is an extremely steep density gradient between the core and the high-entropy hydrogen envelope (Figure 1). Whilst this particular scenario is beset with many uncertainties (Siess Reference Siess2007; Poelarends et al. Reference Poelarends, Herwig, Langer and Heger2008; Jones et al. Reference Jones2013, Reference Jones, Hirschi and Nomoto2014, Reference Jones, Roepke, Pakmor, Seitenzahl, Ohlmann and Edelmann2016a; Doherty et al. Reference Doherty, Gil-Pons, Siess, Lattanzio and Lau2015; Schwab et al. Reference Schwab, Quataert and Bildsten2015; Woosley & Heger Reference Woosley and Heger2015b), recent studies of stellar evolution in the mass range around
$\mathord {{\sim }1.37}\,\text{M}_\odot$
drive the core towards collapse, best exemplifies these peculiarities: Only a small C/O layer is present on top of the core, and the He layer has been effectively whittled down by dredge-up. The consequence is an extremely steep density gradient between the core and the high-entropy hydrogen envelope (Figure 1). Whilst this particular scenario is beset with many uncertainties (Siess Reference Siess2007; Poelarends et al. Reference Poelarends, Herwig, Langer and Heger2008; Jones et al. Reference Jones2013, Reference Jones, Hirschi and Nomoto2014, Reference Jones, Roepke, Pakmor, Seitenzahl, Ohlmann and Edelmann2016a; Doherty et al. Reference Doherty, Gil-Pons, Siess, Lattanzio and Lau2015; Schwab et al. Reference Schwab, Quataert and Bildsten2015; Woosley & Heger Reference Woosley and Heger2015b), recent studies of stellar evolution in the mass range around
![]() $9\,\text{M}_\odot$
have demonstrated that there is a variety of paths towards core-collapse that result in a similar progenitor structure (Jones et al. Reference Jones2013; Woosley & Heger Reference Woosley and Heger2015b), though there is some variation, e.g., in the mass of the remaining He shell due to a different history of dredge-up events. From the perspective of supernova explosion dynamics, the crucial features in the mass range around
$9\,\text{M}_\odot$
have demonstrated that there is a variety of paths towards core-collapse that result in a similar progenitor structure (Jones et al. Reference Jones2013; Woosley & Heger Reference Woosley and Heger2015b), though there is some variation, e.g., in the mass of the remaining He shell due to a different history of dredge-up events. From the perspective of supernova explosion dynamics, the crucial features in the mass range around
![]() $9\,\text{M}_\odot$
are the small mass of the remaining C/O shell and the rapid drop of the density outside the core; both are shared by ECSN progenitors and the lowest iron-core progenitors. This is illustrated in Figure 1 (see also Figure 7 in Jones et al. Reference Jones2013 and Figure 4 in Woosley & Heger Reference Woosley and Heger2015b).
$9\,\text{M}_\odot$
are the small mass of the remaining C/O shell and the rapid drop of the density outside the core; both are shared by ECSN progenitors and the lowest iron-core progenitors. This is illustrated in Figure 1 (see also Figure 7 in Jones et al. Reference Jones2013 and Figure 4 in Woosley & Heger Reference Woosley and Heger2015b).

Figure 1. Density profiles of several low-mass supernova progenitors illustrating the conditions for ECSN-like explosions. Profiles are shown for the
![]() $8.8\,\text{M}_\odot$
ECSN-progenitor of Nomoto (Reference Nomoto1984, Reference Nomoto1987) (N8.8, black), the 8.8
$8.8\,\text{M}_\odot$
ECSN-progenitor of Nomoto (Reference Nomoto1984, Reference Nomoto1987) (N8.8, black), the 8.8
![]() $\text{M}_\odot$
‘failed massive star’ of Jones et al. (Reference Jones2013) (J8.8, purple), low-mass iron-core progenitors (A. Heger, private communication) of
$\text{M}_\odot$
‘failed massive star’ of Jones et al. (Reference Jones2013) (J8.8, purple), low-mass iron-core progenitors (A. Heger, private communication) of
![]() $9.6\,\text{M}_\odot$
(z9.6, with Z=0, red) and
$9.6\,\text{M}_\odot$
(z9.6, with Z=0, red) and
![]() $8.1\,\text{M}_\odot$
(u8.1, with Z = 10−4, blue), and iron progenitors with
$8.1\,\text{M}_\odot$
(u8.1, with Z = 10−4, blue), and iron progenitors with
![]() $10.09\,\text{M}_\odot$
and
$10.09\,\text{M}_\odot$
and
![]() $15\,\text{M}_\odot$
(s10.09 and s15, from Müller et al. Reference Müller, Heger, Liptai and Cameron2016b, yellow and cyan), and
$15\,\text{M}_\odot$
(s10.09 and s15, from Müller et al. Reference Müller, Heger, Liptai and Cameron2016b, yellow and cyan), and
![]() $11.2\,\text{M}_\odot$
(s11.2 from Woosley et al. Reference Woosley, Heger and Weaver2002, green). The thick dashed vertical line roughly denotes the location of the shell that reaches the shock 0.5 s after the onset of collapse. Slanted dashed lines roughly demarcate the regime where the accretion rate onto the shock reaches
$11.2\,\text{M}_\odot$
(s11.2 from Woosley et al. Reference Woosley, Heger and Weaver2002, green). The thick dashed vertical line roughly denotes the location of the shell that reaches the shock 0.5 s after the onset of collapse. Slanted dashed lines roughly demarcate the regime where the accretion rate onto the shock reaches
![]() $0.05\,\text{M}_\odot \, {\rm s}^{-1}$
(thick dashed line),
$0.05\,\text{M}_\odot \, {\rm s}^{-1}$
(thick dashed line),
![]() $5 \times 10^{-3}\,\text{M}_\odot \, {\rm s}^{-1}$
(thin), and
$5 \times 10^{-3}\,\text{M}_\odot \, {\rm s}^{-1}$
(thin), and
![]() $5 \times 10^{-4}\,\text{M}_\odot \, {\rm s}^{-1}$
(thin) (see Section 2.1.2 for details and underlying assumptions). ECSN-like explosion dynamics is expected if the density profile intersects the grey region.
$5 \times 10^{-4}\,\text{M}_\odot \, {\rm s}^{-1}$
(thin) (see Section 2.1.2 for details and underlying assumptions). ECSN-like explosion dynamics is expected if the density profile intersects the grey region.
2.1 Explosion dynamics in ECSN-like progenitors
2.1.1 Classical electron-capture supernova models
The steep density gradient outside the core in ECSN-like progenitors is immediately relevant for the dynamics of the ensuing supernova because it implies a rapid decline of the mass accretion rate
![]() $\dot{M}$
as the edge of the core reaches the stalled accretion shock. A rapid drop in
$\dot{M}$
as the edge of the core reaches the stalled accretion shock. A rapid drop in
![]() $\dot{M}$
implies a decreasing ram pressure ahead of the shock and a continuously increasing shock radius (though the shock remains a stationary accretion shock for at least
$\dot{M}$
implies a decreasing ram pressure ahead of the shock and a continuously increasing shock radius (though the shock remains a stationary accretion shock for at least
![]() $\mathord {\sim } 50\, {\rm ms}$
after bounce and longer for some ECSN-like progenitor models). Under these conditions, neutrino heating can easily pump sufficient energy into the gain region to make the accreted material unbound and power runaway shock expansion. As a result, the neutrino-driven mechanism works for ECSN-like progenitors even under the assumption of spherical symmetry. Using modern multi-group neutrino transport, this was demonstrated by Kitaura et al. (Reference Kitaura, Janka and Hillebrandt2006) for the progenitor of Nomoto (Reference Nomoto1984, Reference Nomoto1987) and confirmed in subsequent simulations by different groups (Janka et al. Reference Janka, Müller, Kitaura and Buras2008; Burrows et al. Reference Burrows, Dessart, Livne, Immler, Weiler and McCray2007b; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010). The explosions are characterised by a small explosion energy of
$\mathord {\sim } 50\, {\rm ms}$
after bounce and longer for some ECSN-like progenitor models). Under these conditions, neutrino heating can easily pump sufficient energy into the gain region to make the accreted material unbound and power runaway shock expansion. As a result, the neutrino-driven mechanism works for ECSN-like progenitors even under the assumption of spherical symmetry. Using modern multi-group neutrino transport, this was demonstrated by Kitaura et al. (Reference Kitaura, Janka and Hillebrandt2006) for the progenitor of Nomoto (Reference Nomoto1984, Reference Nomoto1987) and confirmed in subsequent simulations by different groups (Janka et al. Reference Janka, Müller, Kitaura and Buras2008; Burrows et al. Reference Burrows, Dessart, Livne, Immler, Weiler and McCray2007b; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010). The explosions are characterised by a small explosion energy of
![]() $\mathord {\sim } 10^{50} \, {\rm erg}$
(Kitaura et al. Reference Kitaura, Janka and Hillebrandt2006; Janka et al. Reference Janka, Müller, Kitaura and Buras2008) and a small nickel mass of a few
$\mathord {\sim } 10^{50} \, {\rm erg}$
(Kitaura et al. Reference Kitaura, Janka and Hillebrandt2006; Janka et al. Reference Janka, Müller, Kitaura and Buras2008) and a small nickel mass of a few
![]() $ 10^{-3}\,\text{M}_\odot$
(Wanajo et al. Reference Wanajo, Nomoto, Janka, Kitaura and Müller2009).
$ 10^{-3}\,\text{M}_\odot$
(Wanajo et al. Reference Wanajo, Nomoto, Janka, Kitaura and Müller2009).
Even though multi-dimensional effects are not crucial for shock revival in these models, they are not completely negligible. Higher entropies at the bottom of the gain layer lead to convective overturn driven by Rayleigh–Taylor instability shortly after the explosion is initiated (Wanajo, Janka, & Müller Reference Wanajo, Janka and Müller2011). Simulations in axisymmetry (2D) showed that this leads to a modest increase of the explosion energy in Janka et al. (Reference Janka, Müller, Kitaura and Buras2008); an effect which is somewhat larger in more recent models (von Groote et al., in preparation). The effect of Rayleigh–Taylor overturn on the ejecta composition is, however, much more prominent (see Section 2.2).
2.1.2 Conditions for ECSN-like explosion dynamics
Not all of the newly available supernova progenitor models at the low-mass end (Jones et al. Reference Jones2013, Reference Jones, Hirschi and Nomoto2014; Woosley & Heger Reference Woosley and Heger2015b) exhibit a similarly extreme density profile as the model of Nomoto (Reference Nomoto1984, Reference Nomoto1987); in some of them, the density gradient is considerably more shallow (Figure 1). This prompts the questions: How steep a density gradient is required outside the core to obtain an explosion that is triggered by a rapid drop of the accretion rate and works with no or little help from multi-D effects? In reality, there will obviously be a continuum between ECSN-like events and neutrino-driven explosions of more massive stars, in which multi-D effects are crucial for achieving shock revival. Nonetheless, a rough distinction between the two different regimes is still useful, and can be based on the concept of the critical neutrino luminosity of Burrows & Goshy (Reference Burrows and Goshy1993).
Burrows & Goshy (Reference Burrows and Goshy1993) showed that stationary accretion flow onto a proto-neutron star in spherical symmetry is no longer possible if the neutrino luminosity L
ν (which determines the amount of heating) exceeds a critical value
![]() $L_{\rm crit}(\dot{M})$
that is well approximated by a power law in
$L_{\rm crit}(\dot{M})$
that is well approximated by a power law in
![]() $\dot{M}$
with a small exponent, or, equivalently, if
$\dot{M}$
with a small exponent, or, equivalently, if
![]() $\dot{M}$
drops below a threshold value for a given luminosity. This concept has recently been generalised (Janka Reference Janka2012; Müller & Janka Reference Müller and Janka2015; Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016; Janka, Melson, & Summa Reference Janka, Melson and Summa2016) to a critical relation for the (electron-flavour) neutrino luminosity L
ν and neutrino mean energy E
ν as a function of mass accretion rate
$\dot{M}$
drops below a threshold value for a given luminosity. This concept has recently been generalised (Janka Reference Janka2012; Müller & Janka Reference Müller and Janka2015; Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016; Janka, Melson, & Summa Reference Janka, Melson and Summa2016) to a critical relation for the (electron-flavour) neutrino luminosity L
ν and neutrino mean energy E
ν as a function of mass accretion rate
![]() $\dot{M}$
and proto-neutron star mass M as well as additional correction factors, e.g., for shock expansion due to non-radial instabilities.
$\dot{M}$
and proto-neutron star mass M as well as additional correction factors, e.g., for shock expansion due to non-radial instabilities.
For low-mass progenitors with tenuous shells outside the core, M, L
ν, and E
ν do not depend dramatically on the stellar structure outside the core during the early post-bounce: The proto-neutron star mass is inevitably
![]() $M\approx 1.4\,\text{M}_\odot$
, and since the neutrino emission is dominated by the diffusive neutrino flux from the core, the neutrino emission properties are bound to be similar to the progenitor of Nomoto (Reference Nomoto1984), i.e., one has L
ν ~ 5 × 1052 erg s−1 and E
ν ≈ 11 MeV (Hüdepohl et al. Reference Hüdepohl, Müller, Janka, Marek and Raffelt2009), with a steady decrease of the luminosity towards later times. Using calibrated relations for the ‘heating functional’Footnote
2
L
ν
E
2
ν (Janka et al. Reference Janka, Melson and Summa2016), this translates into a critical mass accretion rate of
$M\approx 1.4\,\text{M}_\odot$
, and since the neutrino emission is dominated by the diffusive neutrino flux from the core, the neutrino emission properties are bound to be similar to the progenitor of Nomoto (Reference Nomoto1984), i.e., one has L
ν ~ 5 × 1052 erg s−1 and E
ν ≈ 11 MeV (Hüdepohl et al. Reference Hüdepohl, Müller, Janka, Marek and Raffelt2009), with a steady decrease of the luminosity towards later times. Using calibrated relations for the ‘heating functional’Footnote
2
L
ν
E
2
ν (Janka et al. Reference Janka, Melson and Summa2016), this translates into a critical mass accretion rate of
![]() $\dot{M}_{\rm crit} \approx 0.07\,\text{M}_\odot \, {\rm s}^{-1}$
for ECSN-like progenitors.
$\dot{M}_{\rm crit} \approx 0.07\,\text{M}_\odot \, {\rm s}^{-1}$
for ECSN-like progenitors.
To obtain similarly rapid shock expansion as for the
![]() $8.8\,\text{M}_\odot$
model of Nomoto (Reference Nomoto1984),
$8.8\,\text{M}_\odot$
model of Nomoto (Reference Nomoto1984),
![]() $\dot{M}$
must rapidly plummet well below this value. This can be translated into a condition for the density profile outside the core using analytic expressions for the infall time t
infall and accretion rate
$\dot{M}$
must rapidly plummet well below this value. This can be translated into a condition for the density profile outside the core using analytic expressions for the infall time t
infall and accretion rate
![]() $\dot{M}$
for mass shell m, which are roughly given by (Woosley & Heger Reference Woosley and Heger2012, Reference Woosley and Heger2015a; Müller et al. Reference Müller, Heger, Liptai and Cameron2016b),
$\dot{M}$
for mass shell m, which are roughly given by (Woosley & Heger Reference Woosley and Heger2012, Reference Woosley and Heger2015a; Müller et al. Reference Müller, Heger, Liptai and Cameron2016b),
and
where
![]() $\bar{\rho }$
is the average density inside the mass shell. For progenitors with little mass outside the core, we have
$\bar{\rho }$
is the average density inside the mass shell. For progenitors with little mass outside the core, we have
Using
![]() $m=1.4\,\text{M}_\odot$
and assuming that
$m=1.4\,\text{M}_\odot$
and assuming that
![]() $\dot{M}$
needs to drop at least to
$\dot{M}$
needs to drop at least to
![]() $M_{\rm crit}=0.05\,\text{M}_\odot \, {\rm s}^{-1}$
within 0.5 s after the onset of collapse to obtain ECSN-like explosion dynamics, one finds that the density needs to drop to
$M_{\rm crit}=0.05\,\text{M}_\odot \, {\rm s}^{-1}$
within 0.5 s after the onset of collapse to obtain ECSN-like explosion dynamics, one finds that the density needs to drop to
for a radius r < 2 230 km.
Figure 1 illustrates that the density gradient at the edge of the core can be far less extreme than in the model of Nomoto (Reference Nomoto1984) to fulfil this criterion. ECSN-like explosion dynamics is expected alike for the modern
![]() $8.8\,\text{M}_\odot$
ECSN progenitor of Jones et al. (Reference Jones2013) and low-mass iron cores (A. Heger, private communication) of
$8.8\,\text{M}_\odot$
ECSN progenitor of Jones et al. (Reference Jones2013) and low-mass iron cores (A. Heger, private communication) of
![]() $8.1\,\text{M}_\odot$
(with metallicity Z = 10−4) and
$8.1\,\text{M}_\odot$
(with metallicity Z = 10−4) and
![]() $9.6\,\text{M}_\odot$
(Z = 0), though the low-mass iron-core progenitors are a somewhat marginal case.
$9.6\,\text{M}_\odot$
(Z = 0), though the low-mass iron-core progenitors are a somewhat marginal case.
2.1.3 Low-mass iron-core progenitors
Simulations of these two low-mass iron progenitors with
![]() $8.1\,\text{M}_\odot$
(Müller, Janka, & Heger Reference Müller, Janka and Heger2012b) and
$8.1\,\text{M}_\odot$
(Müller, Janka, & Heger Reference Müller, Janka and Heger2012b) and
![]() $9.6\,\text{M}_\odot$
(Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Müller et al. Reference Müller, Janka and Marek2013 in 2D; Melson, Janka, & Marek Reference Melson, Janka and Marek2015a in 3D) nonetheless demonstrated that the structure of these stars is sufficiently extreme to produce explosions reminiscent of ECSN models: Shock revival sets in early around 100 ms after bounce, aided by the drop of the accretion rate associated with the infall of the thin O and C/O shells, and the explosion energy remains small (5 × 1049. . .1050 erg).
$9.6\,\text{M}_\odot$
(Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Müller et al. Reference Müller, Janka and Marek2013 in 2D; Melson, Janka, & Marek Reference Melson, Janka and Marek2015a in 3D) nonetheless demonstrated that the structure of these stars is sufficiently extreme to produce explosions reminiscent of ECSN models: Shock revival sets in early around 100 ms after bounce, aided by the drop of the accretion rate associated with the infall of the thin O and C/O shells, and the explosion energy remains small (5 × 1049. . .1050 erg).
As shown by Melson et al. (Reference Melson, Janka and Marek2015a), there are important differences to ECSNe, however: Whilst shock revival also occurs in spherical symmetry, multi-dimensional effects significantly alter the explosion dynamics. In 1D, the shock propagates very slowly through the C/O shell after shock revival, and only accelerates significantly after reaching the He shell. Without the additional boost by convective overturn, the explosion energy is lower by a factor of
![]() $\mathord {\sim } 5$
compared to the multi-D case. Different from ECSNe, somewhat slower shock expansion provides time for the small-scale convective plumes to merge into large structures as shown for the
$\mathord {\sim } 5$
compared to the multi-D case. Different from ECSNe, somewhat slower shock expansion provides time for the small-scale convective plumes to merge into large structures as shown for the
![]() $9.6\,\text{M}_\odot$
model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) in Figure 2.
$9.6\,\text{M}_\odot$
model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) in Figure 2.

Figure 2. Entropy s (left half of plot) and electron fraction
![]() $Y_\text{e}$
(right half) in the
$Y_\text{e}$
(right half) in the
![]() $9.6\,\text{M}_\odot$
explosion model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) and Müller et al. (Reference Müller, Janka and Marek2013) 280 ms after bounce. Large convective plumes push neutron-rich material from close to the gain region out at high velocities.
$9.6\,\text{M}_\odot$
explosion model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) and Müller et al. (Reference Müller, Janka and Marek2013) 280 ms after bounce. Large convective plumes push neutron-rich material from close to the gain region out at high velocities.
Both for the
![]() $8.8\,\text{M}_\odot$
model of Wanajo et al. (Reference Wanajo, Janka and Müller2011) and the low-mass iron-core explosion models, the dynamics of the Rayleigh–Taylor plumes developing after shock revival is nonetheless quite similar. The entropy of the rising plumes is roughly
$8.8\,\text{M}_\odot$
model of Wanajo et al. (Reference Wanajo, Janka and Müller2011) and the low-mass iron-core explosion models, the dynamics of the Rayleigh–Taylor plumes developing after shock revival is nonetheless quite similar. The entropy of the rising plumes is roughly
![]() $\mathord {\sim } 15 \ldots 20 k_{\rm b}/{\rm nucleon}$
compared to
$\mathord {\sim } 15 \ldots 20 k_{\rm b}/{\rm nucleon}$
compared to
![]() $\mathord {\sim }10 k_{\rm b}/{\rm nucleon}$
in the ambient medium. For such an entropy contrast, balance between buoyancy and drag forces applies a limiting velocity of the order of the speed of sound. This limit appears to be reached relatively quickly in the simulations. Apart from the very early growth phase, the plume velocities should therefore not depend strongly on the initial seed perturbations; they are rather set by bulk parameters of the system, namely the post-shock entropy at a few hundred kilometres and the entropy close to the gain radius, which together determine the entropy contrast of the plumes. This will become relevant later in our discussion of the nucleosynthesis of ECSN-like explosions.
$\mathord {\sim }10 k_{\rm b}/{\rm nucleon}$
in the ambient medium. For such an entropy contrast, balance between buoyancy and drag forces applies a limiting velocity of the order of the speed of sound. This limit appears to be reached relatively quickly in the simulations. Apart from the very early growth phase, the plume velocities should therefore not depend strongly on the initial seed perturbations; they are rather set by bulk parameters of the system, namely the post-shock entropy at a few hundred kilometres and the entropy close to the gain radius, which together determine the entropy contrast of the plumes. This will become relevant later in our discussion of the nucleosynthesis of ECSN-like explosions.
2.2 Nucleosynthesis
2.2.1 1D electron-capture supernovae models—early ejecta
Nucleosynthesis calculations based on modern, spherically symmetric ECSN models were first performed by Hoffman, Müller, & Janka (Reference Hoffman, Müller and Janka2008) and Wanajo et al. (Reference Wanajo, Nomoto, Janka, Kitaura and Müller2009). The results of these calculations appeared to point to a severe conflict with observational constraints, showing a strong overproduction of N = 50 nuclei, in particular 90Zr, due to the ejection of slightly neutron-rich material (electron fraction
![]() $Y_\text{e}\gtrsim 0.46$
) with relatively low entropy (s ≈ 18kb
/nucleon) immediately after shock revival. Hoffman et al. (Reference Hoffman, Müller and Janka2008) inferred that such nucleosynthesis yields would only be compatible with chemogalactic evolution if ECSNe were rare events occurring at a rate no larger than once per 3 000 yr.
$Y_\text{e}\gtrsim 0.46$
) with relatively low entropy (s ≈ 18kb
/nucleon) immediately after shock revival. Hoffman et al. (Reference Hoffman, Müller and Janka2008) inferred that such nucleosynthesis yields would only be compatible with chemogalactic evolution if ECSNe were rare events occurring at a rate no larger than once per 3 000 yr.
The low
![]() $Y_\text{e}$
-values in the early ejecta stem from the ejection of matter at relatively high velocities in the wake of the fast-expanding shock. In slow outflows, neutrino absorption on neutrons and protons drives
$Y_\text{e}$
-values in the early ejecta stem from the ejection of matter at relatively high velocities in the wake of the fast-expanding shock. In slow outflows, neutrino absorption on neutrons and protons drives
![]() $Y_\text{e}$
to an equilibrium value that is set by the electron neutrino and anti-neutrino luminosities
$Y_\text{e}$
to an equilibrium value that is set by the electron neutrino and anti-neutrino luminosities
![]() $L_{\nu _\text{e}}$
and
$L_{\nu _\text{e}}$
and
![]() $L_{\bar{\nu }_\text{e}}$
, the ‘effective’ mean energiesFootnote
3
$L_{\bar{\nu }_\text{e}}$
, the ‘effective’ mean energiesFootnote
3
![]() $\varepsilon _{\nu _\text{e}}$
and
$\varepsilon _{\nu _\text{e}}$
and
![]() $\varepsilon _{{\bar{\nu }}_\text{e}}$
, and the proton–neutron mass difference Δ = 1.293 MeV as follows (Qian & Woosley Reference Qian and Woosley1996):
$\varepsilon _{{\bar{\nu }}_\text{e}}$
, and the proton–neutron mass difference Δ = 1.293 MeV as follows (Qian & Woosley Reference Qian and Woosley1996):
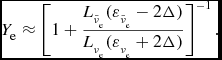 $$\begin{equation}
Y_\text{e} \approx \left[1+\frac{L_{\bar{\nu }_\text{e}} (\varepsilon _{\bar{\nu }_\text{e}}-2 \Delta )}{L_{{\nu }_\text{e}} (\varepsilon _{{\nu }_\text{e}}+2 \Delta )}\right]^{-1}.
\end{equation}$$
$$\begin{equation}
Y_\text{e} \approx \left[1+\frac{L_{\bar{\nu }_\text{e}} (\varepsilon _{\bar{\nu }_\text{e}}-2 \Delta )}{L_{{\nu }_\text{e}} (\varepsilon _{{\nu }_\text{e}}+2 \Delta )}\right]^{-1}.
\end{equation}$$
For the relatively similar electron neutrino and anti-neutrino luminosities and a small difference in the mean energies of 2. . .3 MeV in modern simulations, one typically finds an asymptotic value of
![]() $Y_\text{e}>0.5$
, i.e., proton-rich conditions. To obtain low
$Y_\text{e}>0.5$
, i.e., proton-rich conditions. To obtain low
![]() $Y_\text{e}<0.5$
in the ejecta, neutrino absorption reactions need to freeze out at a high density (small radius) when the equilibrium between the reactions
$Y_\text{e}<0.5$
in the ejecta, neutrino absorption reactions need to freeze out at a high density (small radius) when the equilibrium between the reactions
![]() $n(\nu _\text{e},\text{e}^-)p$
and
$n(\nu _\text{e},\text{e}^-)p$
and
![]() $p(\nu _\text{e},\text{e}^+)n$
is still skewed towards low
$p(\nu _\text{e},\text{e}^+)n$
is still skewed towards low
![]() $Y_\text{e}$
due to electron captures
$Y_\text{e}$
due to electron captures
![]() $p (\text{e}^-,\nu _\text{e}) n$
on protons. Neglecting the difference between arithmetic, quadratic, and cubic neutrino mean energies and assuming a roughly equal contribution of
$p (\text{e}^-,\nu _\text{e}) n$
on protons. Neglecting the difference between arithmetic, quadratic, and cubic neutrino mean energies and assuming a roughly equal contribution of
![]() $n(\nu _\text{e},\text{e}^-)p$
and
$n(\nu _\text{e},\text{e}^-)p$
and
![]() $p(\bar{\nu }_\text{e},\text{e}^+)n$
to the neutrino heating, one can estimate that freeze-out roughly occurs when (cp. Equation (81) in Qian & Woosley Reference Qian and Woosley1996),
$p(\bar{\nu }_\text{e},\text{e}^+)n$
to the neutrino heating, one can estimate that freeze-out roughly occurs when (cp. Equation (81) in Qian & Woosley Reference Qian and Woosley1996),
where
![]() $m_\text{N}$
is the nucleon mass,
$m_\text{N}$
is the nucleon mass,
![]() $\dot{q}_\nu$
is the mass-specific neutrino heating rate, r is the radius, and
$\dot{q}_\nu$
is the mass-specific neutrino heating rate, r is the radius, and
![]() $v_\text{r}$
is the radial velocity. Since
$v_\text{r}$
is the radial velocity. Since
![]() $\dot{q}_\nu \propto r^{-2}$
, freeze-out will occur at smaller r, higher density, and smaller
$\dot{q}_\nu \propto r^{-2}$
, freeze-out will occur at smaller r, higher density, and smaller
![]() $Y_\text{e}$
for higher ejection velocity.
$Y_\text{e}$
for higher ejection velocity.
2.2.2 Multi-D effects and the composition of the early ejecta
Since high ejection velocities translate into lower
![]() $Y_\text{e}$
, the Rayleigh–Taylor plumes in 2D simulations of ECSNe (Figure 2 in Wanajo et al. Reference Wanajo, Janka and Müller2011) and explosions of low-mass iron cores (Figure 2) contain material with even lower
$Y_\text{e}$
, the Rayleigh–Taylor plumes in 2D simulations of ECSNe (Figure 2 in Wanajo et al. Reference Wanajo, Janka and Müller2011) and explosions of low-mass iron cores (Figure 2) contain material with even lower
![]() $Y_\text{e}$
than found in 1D ECSN models. Values of
$Y_\text{e}$
than found in 1D ECSN models. Values of
![]() $Y_\text{e}$
as low as 0.404 are found in Wanajo et al. (Reference Wanajo, Janka and Müller2011).
$Y_\text{e}$
as low as 0.404 are found in Wanajo et al. (Reference Wanajo, Janka and Müller2011).
Surprisingly, Wanajo et al. (Reference Wanajo, Janka and Müller2011) found that the neutron-rich plumes did not aggravate the problematic overproduction of N = 50 nuclei in their 2D ECSN model. This is due to the fact that the entropy in the neutron-rich lumps is actually smaller than in 1DFootnote 4 (but higher than in the ambient medium), which changes the character of the nucleosynthesis by reducing the α-fraction at freeze-out from nuclear statistical equilibrium (NSE). The result is an interesting production of trans-iron elements between Zn and Zr for the progenitor of Nomoto (Reference Nomoto1984, Reference Nomoto1987); the production factors are consistent with current rate estimates for ECSNe of about 4% of all supernovae (Poelarends et al. Reference Poelarends, Herwig, Langer and Heger2008). Subsequent studies showed that neutron-rich lumps in the early ejecta of ECSNe could contribute a sizeable fraction to the live 60Fe in the Galaxy (Wanajo, Janka, & Müller Reference Wanajo, Janka and Müller2013b), and might be production sites for some other rare isotopes of obscure origin, such as 48Ca (Wanajo, Janka, & Müller Reference Wanajo, Janka and Müller2013a). Due to the similar explosion dynamics, low-mass iron-core progenitors exhibit rather similar nucleosynthesis (Wanajo et al., in preparation; Harris et al., in preparation). The results of these nucleosynthesis calculations tallies with the observed abundance trends in metal-poor stars that suggest a separate origin of elements like Sr, Y, and Zr from the heavy r-process elements (light element primary process; Travaglio et al. Reference Travaglio, Gallino, Arnone, Cowan, Jordan and Sneden2004; Wanajo & Ishimaru Reference Wanajo and Ishimaru2006; Qian & Wasserburg Reference Qian and Wasserburg2008; Arcones & Montes Reference Arcones and Montes2011; Hansen et al. Reference Hansen2012; Ting et al. Reference Ting, Freeman, Kobayashi, De Silva and Bland-Hawthorn2012).
Since
![]() $Y_\text{e}$
in the early ejecta of ECSNe and ECSN-like explosion is sensitive to the neutrino luminosities and mean energies and to the ejection velocity of the convective plumes (which may be different in 3D compared to 2D, or exhibit stochastic variations), Wanajo et al. (Reference Wanajo, Janka and Müller2011) also explored the effect of potential uncertainties in the minimum
$Y_\text{e}$
in the early ejecta of ECSNe and ECSN-like explosion is sensitive to the neutrino luminosities and mean energies and to the ejection velocity of the convective plumes (which may be different in 3D compared to 2D, or exhibit stochastic variations), Wanajo et al. (Reference Wanajo, Janka and Müller2011) also explored the effect of potential uncertainties in the minimum
![]() $Y_\text{e}$
in the ejecta on the nucleosynthesis. They found that a somewhat lower
$Y_\text{e}$
in the ejecta on the nucleosynthesis. They found that a somewhat lower
![]() $Y_\text{e}$
of ~ 0.3 in the plumes might make ECSNe a site for a ‘weak r-process’ that could explain the enhanced abundances of lighter r-process elements up to Ag and Pd in some metal-poor halo stars (Wanajo & Ishimaru Reference Wanajo and Ishimaru2006; Honda et al. Reference Honda, Aoki, Ishimaru, Wanajo and Ryan2006).
$Y_\text{e}$
of ~ 0.3 in the plumes might make ECSNe a site for a ‘weak r-process’ that could explain the enhanced abundances of lighter r-process elements up to Ag and Pd in some metal-poor halo stars (Wanajo & Ishimaru Reference Wanajo and Ishimaru2006; Honda et al. Reference Honda, Aoki, Ishimaru, Wanajo and Ryan2006).
Whether the neutron-rich conditions required for a weak r-process can be achieved in ECSNe or low-mass iron-core supernovae remains to be determined. Figure 3 provides a tentative glimpse on the effects of stochasticity and dimensionality on the
![]() $Y_\text{e}$
in neutron-rich plumes based on several 2D and 3D explosion models of a
$Y_\text{e}$
in neutron-rich plumes based on several 2D and 3D explosion models of a
![]() $9.6\,\text{M}_\odot$
low-mass iron-core progenitor (A. Heger, private communication) conducted using the FMT transport scheme of Müller & Janka (Reference Müller and Janka2015).Footnote
5
Stochastic variations in 2D models due to different (random) initial perturbations shift the minimum
$9.6\,\text{M}_\odot$
low-mass iron-core progenitor (A. Heger, private communication) conducted using the FMT transport scheme of Müller & Janka (Reference Müller and Janka2015).Footnote
5
Stochastic variations in 2D models due to different (random) initial perturbations shift the minimum
![]() $Y_\text{e}$
in the ejecta at most by 0.02. This is due to the fact that the Rayleigh–Taylor plumes rapidly transition from the initial growth phase to a stage where buoyancy and drag balance each other and determine the velocity (Alon et al. Reference Alon, Hecht, Ofer and Shvarts1995). 3D effects do not change the distribution of
$Y_\text{e}$
in the ejecta at most by 0.02. This is due to the fact that the Rayleigh–Taylor plumes rapidly transition from the initial growth phase to a stage where buoyancy and drag balance each other and determine the velocity (Alon et al. Reference Alon, Hecht, Ofer and Shvarts1995). 3D effects do not change the distribution of
![]() $Y_\text{e}$
tremendously either, at best they tend to shift it to slightly higher values compared to 2D, which is consistent with a somewhat stronger braking of expanding bubbles in 3D as a result of the forward turbulent cascade (Melson et al. Reference Melson, Janka and Marek2015a). It thus appears unlikely that the dynamics of convective overturn is a major source of uncertainty for the nucleosynthesis in ECSN-like explosions, though confirmation with better neutrino transport is still needed.
$Y_\text{e}$
tremendously either, at best they tend to shift it to slightly higher values compared to 2D, which is consistent with a somewhat stronger braking of expanding bubbles in 3D as a result of the forward turbulent cascade (Melson et al. Reference Melson, Janka and Marek2015a). It thus appears unlikely that the dynamics of convective overturn is a major source of uncertainty for the nucleosynthesis in ECSN-like explosions, though confirmation with better neutrino transport is still needed.

Figure 3. Binned distribution of the electron fraction
![]() $Y_\text{e}$
in the early ejecta for different explosion models of a
$Y_\text{e}$
in the early ejecta for different explosion models of a
![]() $9.6\,\text{M}_\odot$
star 270 ms after bounce. The plots show the relative contribution ΔM
ej/M
ej to the total mass of (shocked) ejecta in bins with
$9.6\,\text{M}_\odot$
star 270 ms after bounce. The plots show the relative contribution ΔM
ej/M
ej to the total mass of (shocked) ejecta in bins with
![]() $\Delta Y_\text{e}=0.01$
. The upper panel shows the
$\Delta Y_\text{e}=0.01$
. The upper panel shows the
![]() $Y_\text{e}$
-distribution for the 2D model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) computed using the vertex-coconut code (Müller et al. Reference Müller, Janka and Dimmelmeier2010). The bottom panel illustrates the effect of stochastic variations and dimensionality using several 2D models (thin lines) and a 3D model computed with the coconut-fmt code of Müller & Janka (Reference Müller and Janka2015) (thick lines). Note that the dispersion in
$Y_\text{e}$
-distribution for the 2D model of Janka et al. (Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012) computed using the vertex-coconut code (Müller et al. Reference Müller, Janka and Dimmelmeier2010). The bottom panel illustrates the effect of stochastic variations and dimensionality using several 2D models (thin lines) and a 3D model computed with the coconut-fmt code of Müller & Janka (Reference Müller and Janka2015) (thick lines). Note that the dispersion in
![]() $Y_\text{e}$
in the early ejecta is similar for both codes, though the average
$Y_\text{e}$
in the early ejecta is similar for both codes, though the average
![]() $Y_\text{e}$
in the early ejecta is spuriously low when less accurate neutrino transport is used (fmt instead of Vertex). The bottom panel is therefore only intended to show differential effects between different models, and is not a prediction of the absolute value of
$Y_\text{e}$
in the early ejecta is spuriously low when less accurate neutrino transport is used (fmt instead of Vertex). The bottom panel is therefore only intended to show differential effects between different models, and is not a prediction of the absolute value of
![]() $Y_\text{e}$
. It suggests that (i) stochastic variations do not strongly affect the distribution of
$Y_\text{e}$
. It suggests that (i) stochastic variations do not strongly affect the distribution of
![]() $Y_\text{e}$
in the ejecta, and that (ii) the resulting distribution of
$Y_\text{e}$
in the ejecta, and that (ii) the resulting distribution of
![]() $Y_\text{e}$
in 2D and 3D is relatively similar.
$Y_\text{e}$
in 2D and 3D is relatively similar.
If these events are indeed sites of a weak r-process, the missing ingredient is likely to be found elsewhere. Improvements in the neutrino opacities, such as the proper inclusion of nucleon potentials in the charged-current interaction rates (Martínez-Pinedo et al. Reference Martínez-Pinedo, Fischer, Lohs and Huther2012; Roberts, Reddy, & Shen Reference Roberts, Reddy and Shen2012), or flavour oscillations involving sterile neutrinos (Wu et al. Reference Wu, Fischer, Huther, Martínez-Pinedo and Qian2014) could lower
![]() $Y_\text{e}$
somewhat. Wu et al. (Reference Wu, Fischer, Huther, Martínez-Pinedo and Qian2014) found a significant reduction of
$Y_\text{e}$
somewhat. Wu et al. (Reference Wu, Fischer, Huther, Martínez-Pinedo and Qian2014) found a significant reduction of
![]() $Y_\text{e}$
by up to 0.15 in some of the ejecta, but these results may depend sensitively on the assumption that collective flavour oscillations are still suppressed during the phase in question. Moreover, Wu et al. (Reference Wu, Fischer, Huther, Martínez-Pinedo and Qian2014) pointed out that a reduction of
$Y_\text{e}$
by up to 0.15 in some of the ejecta, but these results may depend sensitively on the assumption that collective flavour oscillations are still suppressed during the phase in question. Moreover, Wu et al. (Reference Wu, Fischer, Huther, Martínez-Pinedo and Qian2014) pointed out that a reduction of
![]() $Y_\text{e}$
with the help of active-sterile flavour conversion might require delicate fine-tuning to avoid shutting off neutrino heating before the onset of the explosion due to the disappearance of
$Y_\text{e}$
with the help of active-sterile flavour conversion might require delicate fine-tuning to avoid shutting off neutrino heating before the onset of the explosion due to the disappearance of
![]() $\nu _\text{e}$
’s (which could be fatal to the explosion mechanism).
$\nu _\text{e}$
’s (which could be fatal to the explosion mechanism).
Moreover, whether ECSNe necessarily need to co-produce Ag and Pd with Sr, Y, and Zr is by no means clear. Whilst observed abundance trends may suggest such a co-production, the abundance patterns of elements between Sr and Ag in metal-poor stars appear less robust (Hansen, Montes, & Arcones Reference Hansen, Montes and Arcones2014); and the failure of unaltered models to produce Ag and Pd may not be indicative of a severe tension with observations.
2.2.3 Other nucleosynthesis scenarios for electron-capture supernovae
There are at least two other potentially interesting sites for nucleosynthesis in ECSN-like supernovae. For ‘classical’ ECSN-progenitors with more extreme density profiles, it has been proposed that the rapid acceleration of the shock in the steep density gradient outside the core can lead to sufficiently high post-shock entropies (s ~ 100 kb /nucleon) and short expansion time-scales (τexp ~ 10−4 s) to allow r-process nucleosynthesis in the thin shells outside the core (Ning, Qian, & Meyer Reference Ning, Qian and Meyer2007). This has not been borne out by numerical simulations, however (Janka et al. Reference Janka, Müller, Kitaura and Buras2008; Hoffman et al. Reference Hoffman, Müller and Janka2008). When the requisite high entropy is reached, the post-shock temperature has already dropped far too low to dissociate nuclei, and the expansion timescale does not become sufficiently short for the scenario of Ning et al. (Reference Ning, Qian and Meyer2007) to work. The proposed r-process in the rapidly expanding shocked shells would require significantly different explosion dynamics, e.g., a much higher explosion energy.
The neutrino-driven wind that is launched after accretion onto the proto-neutron star has been completely subsided has long been discussed as a potential site of r-process nucleosynthesis in supernovae (Woosley et al. Reference Woosley, Wilson, Mathews and Hoffman1994; Takahashi, Witti, & Janka Reference Takahashi, Witti and Janka1994; Qian & Woosley Reference Qian and Woosley1996; Cardall & Fuller Reference Cardall and Fuller1997; Thompson, Burrows, & Meyer Reference Thompson, Burrows and Meyer2001; Arcones, Janka, & Scheck Reference Arcones, Janka and Scheck2007; Arcones & Thielemann Reference Arcones and Thielemann2013). ECSN-like explosions are in many respects the least favourable site for an r-process in the neutrino-driven wind since they produce low-mass neutron stars, which implies low wind entropies and long expansion timescales (Qian & Woosley Reference Qian and Woosley1996), i.e., conditions that are detrimental to r-process nucleosynthesis. However, ECSNe are unique in as much as the neutrino-driven wind can be calculated self-consistently with Boltzmann neutrino transport (Hüdepohl et al. Reference Hüdepohl, Müller, Janka, Marek and Raffelt2009; Fischer et al. Reference Fischer, Whitehouse, Mezzacappa, Thielemann and Liebendörfer2010) without the need to trigger an explosion artificially. These simulations revealed a neutrino-driven wind that is not only of moderate entropy (s ≲ 140kb /nucleon even at late times), but also becomes increasingly proton-rich with time, in which case the νp-process (Fröhlich et al. Reference Fröhlich, Martínez-Pinedo, Liebendörfer, Thielemann, Bravo, Hix, Langanke and Zinner2006) could potentially operate. The most rigorous nucleosynthesis calculations for the neutrino-driven wind in ECSNe so far (Pllumbi et al. Reference Pllumbi, Tamborra, Wanajo and Janka2015) are based on simulations that properly account for nucleon interaction potentials in the neutrino opacities (Martínez-Pinedo et al. Reference Martínez-Pinedo, Fischer, Lohs and Huther2012; Roberts et al. Reference Roberts, Reddy and Shen2012) and have also explored the effects of collective flavour oscillations, active-sterile flavour conversion. Pllumbi et al. (Reference Pllumbi, Tamborra, Wanajo and Janka2015) suggest that wind nucleosynthesis in ECSNe is rather mundane: Neither does the νp-process operate nor can neutron-rich conditions be restored to obtain conditions even for a weak r-process. Instead, they find that wind nucleosynthesis mainly produces nuclei between Sc and Zn, but the production factors are low, implying that the role of neutrino-driven winds in ECSNe is negligible for this mass range for the purpose of chemogalactic evolution.
2.3 Electron-capture supernovae—transients and remnants
Although the explosion mechanism of ECSNe is in many respects best understood amongst all CCSN types from the viewpoint of explosion mechanism, unambiguously identifying transients as ECSNe has proved more difficult. It has long been proposed that SN 1054 was an ECSN (Nomoto et al. Reference Nomoto, Sugimoto, Sparks, Fesen, Gull and Miyaji1982) based on the properties of its remnant, the Crab nebula: The total mass of ejecta in the nebula is small (
![]() ${\lesssim }5\,\text{M}_\odot$
; Davidson & Fesen Reference Davidson and Fesen1985; MacAlpine & Uomoto Reference MacAlpine and Uomoto1991; Fesen, Shull, & Hurford Reference Fesen, Shull and Hurford1997), as is the oxygen abundance (Davidson et al. Reference Davidson1982; Henry & MacAlpine Reference Henry and MacAlpine1982; Henry Reference Henry1986), which is in line with the thin O-rich shells in ECSN progenitors. Moreover, the kinetic energy of the ejecta is only about ≲ 1050 erg (Fesen et al. Reference Fesen, Shull and Hurford1997; Hester Reference Hester2008) as expected for an ECSN-like event. Whether the Crab originates from a classical ECSN or from something slightly different like a ‘failed massive star’ of Jones et al. (Reference Jones2013) continues to be debated; MacAlpine & Satterfield (Reference MacAlpine and Satterfield2008) have argued, for example, against the former interpretation based on a high abundance ratio of C vs. N and the detection of some ashes of oxygen burning (S, Ar) in the nebula.
${\lesssim }5\,\text{M}_\odot$
; Davidson & Fesen Reference Davidson and Fesen1985; MacAlpine & Uomoto Reference MacAlpine and Uomoto1991; Fesen, Shull, & Hurford Reference Fesen, Shull and Hurford1997), as is the oxygen abundance (Davidson et al. Reference Davidson1982; Henry & MacAlpine Reference Henry and MacAlpine1982; Henry Reference Henry1986), which is in line with the thin O-rich shells in ECSN progenitors. Moreover, the kinetic energy of the ejecta is only about ≲ 1050 erg (Fesen et al. Reference Fesen, Shull and Hurford1997; Hester Reference Hester2008) as expected for an ECSN-like event. Whether the Crab originates from a classical ECSN or from something slightly different like a ‘failed massive star’ of Jones et al. (Reference Jones2013) continues to be debated; MacAlpine & Satterfield (Reference MacAlpine and Satterfield2008) have argued, for example, against the former interpretation based on a high abundance ratio of C vs. N and the detection of some ashes of oxygen burning (S, Ar) in the nebula.
It has been recognised in recent years that the (reconstructed) light curve of SN 1054—a type IIP supernova with a relatively bright plateau—is also compatible with the low explosion energy of ≲ 1050 erg predicted by recent numerical simulations. Smith (Reference Smith2013) interpreted the bright plateau, which made SN 1054 visible by daytime for
![]() $\mathord {\sim } 3 \ {\rm weeks}$
, as the result of interaction with circumstellar medium (CSM). The scenario of Smith (Reference Smith2013) requires significant mass loss (
$\mathord {\sim } 3 \ {\rm weeks}$
, as the result of interaction with circumstellar medium (CSM). The scenario of Smith (Reference Smith2013) requires significant mass loss (
![]() $0.1\,\text{M}_\odot$
for about 30 yr) shortly before the supernova, which may be difficult to achieve, although some channels towards ECSN-like explosions could involve dramatic mass loss events (Woosley & Heger Reference Woosley and Heger2015b). Subsequent numerical calculations of ECSN light curves (Tominaga, Blinnikov, & Nomoto Reference Tominaga, Blinnikov and Nomoto2013; Moriya et al. Reference Moriya, Tominaga, Langer, Nomoto, Blinnikov and Sorokina2014) demonstrated, however, that less extreme assumptions for the mass loss are required to explain the optical signal of SN 1054; indeed a very extended hydrogen envelope may be sufficient to explain the bright plateau, and CSM interaction with the progenitor wind may only be required to prevent the SN from fading too rapidly.
$0.1\,\text{M}_\odot$
for about 30 yr) shortly before the supernova, which may be difficult to achieve, although some channels towards ECSN-like explosions could involve dramatic mass loss events (Woosley & Heger Reference Woosley and Heger2015b). Subsequent numerical calculations of ECSN light curves (Tominaga, Blinnikov, & Nomoto Reference Tominaga, Blinnikov and Nomoto2013; Moriya et al. Reference Moriya, Tominaga, Langer, Nomoto, Blinnikov and Sorokina2014) demonstrated, however, that less extreme assumptions for the mass loss are required to explain the optical signal of SN 1054; indeed a very extended hydrogen envelope may be sufficient to explain the bright plateau, and CSM interaction with the progenitor wind may only be required to prevent the SN from fading too rapidly.
Several other transients have also been interpreted as ECSNe, e.g., faint type IIP supernovae such as SN 2008S (Botticella et al. Reference Botticella2009). Smith (Reference Smith2013) posits that ECSNe are observed type IIn-P supernovae with circumstellar interaction like SN 1994W with a bright plateau and a relatively sharp drop to a faint nickel-powered tail, but again the required amount of CSM is not easy to explain. All of these candidate events share low kinetic energies and small nickel masses as a common feature and are thus prima facie compatible with ECSN-like explosion dynamics. Variations in the envelope structure of ECSN-progenitors (e.g., envelope stripping in binaries) may account for the very different optical signatures (Moriya et al. Reference Moriya, Tominaga, Langer, Nomoto, Blinnikov and Sorokina2014).
The peculiar nucleosynthesis in ECSNe-like explosions may also leave observable fingerprints in the electromagnetic signatures. The slightly neutron-rich character of the early ejecta results in a strongly supersolar abundance ratio of Ni to Fe after β-decays are completed (Wanajo et al. Reference Wanajo, Janka and Müller2011). Such high Ni/Fe ratios are seen in the nebular spectra of some supernovae (Jerkstrand et al. Reference Jerkstrand2015a, Reference Jerkstrand2015b). ECSNe can only explain some of these events; however, many of them exhibit explosion energies and Nickel masses that are incompatible with an ECSN.
3 3D SUPERNOVA MODELS OF MASSIVE PROGENITORS
In more massive progenitors with extended Si and O shells, the mass accretion rate onto the shock does not drop as rapidly as in ECSN-like explosions. Typically, one finds a relatively stable accretion rate of a few
![]() $0.1\,\text{M}_\odot \, {\rm s}^{-1}$
during the infall of the O shell, which implies a high ram pressure ahead of the shock. Under these conditions, it is no longer trivial to demonstrate that neutrino heating can pump a sufficient amount of energy into the post-shock region to power runaway shock expansion. 1D simulations of the post-bounce phase using Boltzmann solvers for the neutrino transport convincingly demonstrated that neutrino-driven explosions cannot be obtained under such conditions in spherical symmetry (Liebendörfer et al. Reference Liebendörfer, Mezzacappa, Thielemann, Messer, Hix and Bruenn2001; Rampp & Janka Reference Rampp and Janka2000; Burrows et al. Reference Burrows, Young, Pinto, Eastman and Thompson2000a). Much of the work of recent years has therefore focussed on better understanding and accurately modelling how multi-dimensional effects in supernovae facilitate neutrino-driven explosions—an undertaking first begun in the 1990s with axisymmetric (2D) simulations employing various approximations for neutrino heating and cooling (Herant, Benz, & Colgate Reference Herant, Benz and Colgate1992; Yamada, Shimizu, & Sato Reference Yamada, Shimizu and Sato1993; Herant et al. Reference Herant, Benz, Hix, Fryer and Colgate1994; Burrows et al. Reference Burrows, Hayes and Fryxell1995; Janka & Müller Reference Janka and Müller1995, Reference Janka and Müller1996). 2D simulations have by now matured to the point that multi-group neutrino transport and the neutrino-matter interactions can be modelled with the same rigour as in spherical symmetry (Livne et al. Reference Livne, Burrows, Walder and Lichtenstadt2004; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a; Müller et al. Reference Müller, Janka and Dimmelmeier2010; Bruenn et al. Reference Bruenn2013; Just, Obergaulinger, & Janka Reference Just, Obergaulinger and Janka2015; Skinner, Burrows, & Dolence Reference Skinner, Burrows and Dolence2016), or with, still with acceptable accuracy for many purposes (see Section 4 for a more careful discussion), by using some approximations either in the transport treatment or the neutrino microphysics (Suwa et al. Reference Suwa, Kotake, Takiwaki, Whitehouse, Liebendörfer and Sato2010; Müller & Janka Reference Müller and Janka2015; Pan et al. Reference Pan, Liebendörfer, Hempel and Thielemann2016; O’Connor & Couch Reference O’Connor and Couch2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016).
$0.1\,\text{M}_\odot \, {\rm s}^{-1}$
during the infall of the O shell, which implies a high ram pressure ahead of the shock. Under these conditions, it is no longer trivial to demonstrate that neutrino heating can pump a sufficient amount of energy into the post-shock region to power runaway shock expansion. 1D simulations of the post-bounce phase using Boltzmann solvers for the neutrino transport convincingly demonstrated that neutrino-driven explosions cannot be obtained under such conditions in spherical symmetry (Liebendörfer et al. Reference Liebendörfer, Mezzacappa, Thielemann, Messer, Hix and Bruenn2001; Rampp & Janka Reference Rampp and Janka2000; Burrows et al. Reference Burrows, Young, Pinto, Eastman and Thompson2000a). Much of the work of recent years has therefore focussed on better understanding and accurately modelling how multi-dimensional effects in supernovae facilitate neutrino-driven explosions—an undertaking first begun in the 1990s with axisymmetric (2D) simulations employing various approximations for neutrino heating and cooling (Herant, Benz, & Colgate Reference Herant, Benz and Colgate1992; Yamada, Shimizu, & Sato Reference Yamada, Shimizu and Sato1993; Herant et al. Reference Herant, Benz, Hix, Fryer and Colgate1994; Burrows et al. Reference Burrows, Hayes and Fryxell1995; Janka & Müller Reference Janka and Müller1995, Reference Janka and Müller1996). 2D simulations have by now matured to the point that multi-group neutrino transport and the neutrino-matter interactions can be modelled with the same rigour as in spherical symmetry (Livne et al. Reference Livne, Burrows, Walder and Lichtenstadt2004; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a; Müller et al. Reference Müller, Janka and Dimmelmeier2010; Bruenn et al. Reference Bruenn2013; Just, Obergaulinger, & Janka Reference Just, Obergaulinger and Janka2015; Skinner, Burrows, & Dolence Reference Skinner, Burrows and Dolence2016), or with, still with acceptable accuracy for many purposes (see Section 4 for a more careful discussion), by using some approximations either in the transport treatment or the neutrino microphysics (Suwa et al. Reference Suwa, Kotake, Takiwaki, Whitehouse, Liebendörfer and Sato2010; Müller & Janka Reference Müller and Janka2015; Pan et al. Reference Pan, Liebendörfer, Hempel and Thielemann2016; O’Connor & Couch Reference O’Connor and Couch2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016).
3.1 Prelude—first-principle 2D models
The current generation of 2D supernova simulations with multi-group neutrino transport has gone a long way towards demonstrating that neutrino heating can bring about explosion in conjunction with convection or the SASI. Thanks to steadily growing computational resources, the range of successful neutrino-driven explosion models has grown from about a handful in mid-2012 (Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Marek & Janka Reference Marek and Janka2009; Suwa et al. Reference Suwa, Kotake, Takiwaki, Whitehouse, Liebendörfer and Sato2010; Müller, Janka, & Marek Reference Müller, Janka and Marek2012a) to a huge sample of explosion models with ZAMS masses between 10 and
![]() $ 75\,\text{M}_\odot$
, different metallicities, and different choices for the supranuclear equation of state (Müller et al. Reference Müller, Janka and Heger2012b; Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Suwa et al. Reference Suwa, Takiwaki, Kotake, Fischer, Liebendörfer and Sato2013; Bruenn et al. Reference Bruenn2013; Obergaulinger, Janka, & Aloy Reference Obergaulinger, Janka and Aloy2014; Nakamura et al. Reference Nakamura, Takiwaki, Kuroda and Kotake2015; Müller Reference Müller2015; Bruenn et al. Reference Bruenn2016; O’Connor & Couch Reference O’Connor and Couch2015; Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016; Pan et al. Reference Pan, Liebendörfer, Hempel and Thielemann2016).
$ 75\,\text{M}_\odot$
, different metallicities, and different choices for the supranuclear equation of state (Müller et al. Reference Müller, Janka and Heger2012b; Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Suwa et al. Reference Suwa, Takiwaki, Kotake, Fischer, Liebendörfer and Sato2013; Bruenn et al. Reference Bruenn2013; Obergaulinger, Janka, & Aloy Reference Obergaulinger, Janka and Aloy2014; Nakamura et al. Reference Nakamura, Takiwaki, Kuroda and Kotake2015; Müller Reference Müller2015; Bruenn et al. Reference Bruenn2016; O’Connor & Couch Reference O’Connor and Couch2015; Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016; Pan et al. Reference Pan, Liebendörfer, Hempel and Thielemann2016).
Many of the findings from these simulations remain important and valid after the advent of 3D modelling: The 2D models have established, amongst other things, the existence of distinct SASI- and convection-dominated regimes in the accretion phase, both of which can lead to successful explosion (Müller et al. Reference Müller, Janka and Heger2012b) in agreement with tunable, parameterised models (Scheck et al. Reference Scheck, Janka, Foglizzo and Kifonidis2008; Fernández et al. Reference Fernández, Müller, Foglizzo and Janka2014). They have shown that ‘softer’ nuclear equations of state that result in more compact neutron stars are generally favourable for shock revival (Janka Reference Janka2012; Suwa et al. Reference Suwa, Takiwaki, Kotake, Fischer, Liebendörfer and Sato2013; Couch Reference Couch2013a). The inclusion of general relativistic effects, whether by means of the conformally flat approximation (CFC) or, less rigorously, an effective pseudo-relativistic potential for Newtonian hydrodynamics, was found to have a similarly beneficial effect (CFC: Müller et al. Reference Müller, Janka and Marek2012a; pseudo-Newtonian: O’Connor & Couch Reference O’Connor and Couch2015). Moreover, there are signs that the 2D models of some groups converge with each other; simulations of four different stellar models (
![]() $12,15,20,25\,\text{M}_\odot$
) of Woosley & Heger (Reference Woosley and Heger2007) by Summa et al. (Reference Summa, Hanke, Janka, Melson, Marek and Müller2016) and O’Connor & Couch (Reference O’Connor and Couch2015) have yielded quantitatively similar results.
$12,15,20,25\,\text{M}_\odot$
) of Woosley & Heger (Reference Woosley and Heger2007) by Summa et al. (Reference Summa, Hanke, Janka, Melson, Marek and Müller2016) and O’Connor & Couch (Reference O’Connor and Couch2015) have yielded quantitatively similar results.
Despite these successes, 2D models have, by and large, struggled to reproduce the typical explosion properties of supernovae. They are often characterised by a slow and unsteady growth of the explosion energy after shock revival. Usually the growth of the explosion energy cannot be followed beyond 2. . .4 × 1050 erg after simulating up to
![]() $\mathord {\sim } 1 \, {\rm s}$
of physical time (Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Nakamura et al. Reference Nakamura, Takiwaki, Kuroda and Kotake2015; O’Connor & Couch Reference O’Connor and Couch2015), i.e., below typical observed values of 5. . .9 × 1050 erg (Kasen & Woosley Reference Kasen and Woosley2009; Pejcha & Prieto Reference Pejcha and Prieto2015). Only the models of Bruenn et al. (Reference Bruenn2016) reach significantly higher explosion energies. Whilst the explosion energy often has not levelled out yet at the end of the simulations and may still grow significantly for several seconds (Müller Reference Müller2015), its continuing growth comes at the expense of long-lasting accretion onto the proto-neutron star. This may result in inordinately high remnant masses. Thus, whilst 2D models appeared to have solved the problem of shock revival, they faced an energy problem instead.
$\mathord {\sim } 1 \, {\rm s}$
of physical time (Janka et al. Reference Janka, Hanke, Hüdepohl, Marek, Müller and Obergaulinger2012; Nakamura et al. Reference Nakamura, Takiwaki, Kuroda and Kotake2015; O’Connor & Couch Reference O’Connor and Couch2015), i.e., below typical observed values of 5. . .9 × 1050 erg (Kasen & Woosley Reference Kasen and Woosley2009; Pejcha & Prieto Reference Pejcha and Prieto2015). Only the models of Bruenn et al. (Reference Bruenn2016) reach significantly higher explosion energies. Whilst the explosion energy often has not levelled out yet at the end of the simulations and may still grow significantly for several seconds (Müller Reference Müller2015), its continuing growth comes at the expense of long-lasting accretion onto the proto-neutron star. This may result in inordinately high remnant masses. Thus, whilst 2D models appeared to have solved the problem of shock revival, they faced an energy problem instead.
3.2 Status of 3D core-collapse supernova models
Before 3D modelling began in earnest (leaving aside tentative sallies into 3D by Fryer & Warren Reference Fryer and Warren2002), it was hoped that 3D effects might facilitate shock revival even at earlier times than in 2D, and that this might then also provide a solution to the energy problem, since more energy can be pumped into the neutrino-heated ejecta at early times when the mass in the gain region is larger. These hopes were already disappointed once several groups investigated the role of 3D effects in the explosion mechanism using a simple ‘light-bulb’ approach, where the neutrino luminosity and mean energy during the accretion phase are prescribed and very simple approximations for the neutrino heating and cooling terms are employed. Although Nordhaus et al. (Reference Nordhaus, Burrows, Almgren and Bell2010) initially claimed a significant reduction of the critical neutrino luminosity for shock revival in 3D compared to 2D based on such an approach, these results were affected by the gravity treatment (Burrows, Dolence, & Murphy Reference Burrows, Dolence and Murphy2012) and have not been confirmed by subsequent studies. Similar parameterised simulations have shown that the critical luminosity in 3D is roughly equal to 2D (Hanke et al. Reference Hanke, Marek, Müller and Janka2012; Couch Reference Couch2013b; Burrows et al. Reference Burrows, Dolence and Murphy2012; Dolence et al. Reference Dolence, Burrows, Murphy and Nordhaus2013) and about 20% lower than in 1D, though the results differ about the hierarchy between 2D and 3D.
Subsequent supernova models based on multi-group neutrino transport yielded even more unambiguous results: Shock revival in 3D was either not achieved for progenitors that explode in 2D (Hanke et al. Reference Hanke, Müller, Wongwathanarat, Marek and Janka2013; Tamborra et al. Reference Tamborra, Hanke, Janka, Müller, Raffelt and Marek2014b), or was delayed significantly (Takiwaki, Kotake, & Suwa Reference Takiwaki, Kotake and Suwa2014; Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b; Lentz et al. Reference Lentz2015). These first disappointing results need to be interpreted carefully, however: A detailed analysis of the heating conditions in the non-exploding 3D models of 11.2, 20, and
![]() $27\,\text{M}_\odot$
progenitors simulated by the Garching supernova group revealed that these are very close to shock revival (Hanke et al. Reference Hanke, Müller, Wongwathanarat, Marek and Janka2013; Hanke Reference Hanke2014; Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b). Moreover, the 3D models of the Garching group are characterised by more optimistic heating conditions, larger average shock radii, and higher kinetic energies in non-spherical motions compared to 2D for extended periods of time; the same is true for the delayed (compared to 2D) 3D explosion of Lentz et al. (Reference Lentz2015) of a
$27\,\text{M}_\odot$
progenitors simulated by the Garching supernova group revealed that these are very close to shock revival (Hanke et al. Reference Hanke, Müller, Wongwathanarat, Marek and Janka2013; Hanke Reference Hanke2014; Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b). Moreover, the 3D models of the Garching group are characterised by more optimistic heating conditions, larger average shock radii, and higher kinetic energies in non-spherical motions compared to 2D for extended periods of time; the same is true for the delayed (compared to 2D) 3D explosion of Lentz et al. (Reference Lentz2015) of a
![]() $15\,\text{M}_\odot$
progenitor. It is merely when it comes to sustaining shock expansion that the 3D models prove less resilient than their 2D counterparts, which transition into an explosive runaway more robustly.
$15\,\text{M}_\odot$
progenitor. It is merely when it comes to sustaining shock expansion that the 3D models prove less resilient than their 2D counterparts, which transition into an explosive runaway more robustly.
The conclusion that 3D models are only slightly less prone to explosion is reinforced by the emergence of the first successful simulations of shock revival in progenitors with
![]() $20\,\text{M}_\odot$
(Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) and
$20\,\text{M}_\odot$
(Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) and
![]() $15\,\text{M}_\odot$
(Lentz et al. Reference Lentz2015) using rigorous multi-group neutrino transport and the best available neutrino interaction rates. There is also a number of 3D explosion models based on more simplified approaches to multi-group neutrino transport (Takiwaki, Kotake, & Suwa Reference Takiwaki, Kotake and Suwa2012; Takiwaki et al. Reference Takiwaki, Kotake and Suwa2014; Müller Reference Müller2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016).
$15\,\text{M}_\odot$
(Lentz et al. Reference Lentz2015) using rigorous multi-group neutrino transport and the best available neutrino interaction rates. There is also a number of 3D explosion models based on more simplified approaches to multi-group neutrino transport (Takiwaki, Kotake, & Suwa Reference Takiwaki, Kotake and Suwa2012; Takiwaki et al. Reference Takiwaki, Kotake and Suwa2014; Müller Reference Müller2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016).
3.3 How do multi-D effects facilitate shock revival?
Despite these encouraging developments, several questions now need to be addressed to make further progress: What is the key to robust 3D explosion models across the entire progenitor mass range for which we observe explosions (i.e., at least up to
![]() $15 \ldots 18\,\text{M}_\odot$
; see Smartt et al. Reference Smartt, Eldridge, Crockett and Maund2009 and Smartt Reference Smartt2015)? This question is tightly connected to another, more fundamental one, namely: What are the conditions for an explosive runaway, and how do multi-dimensional effects modify them?
$15 \ldots 18\,\text{M}_\odot$
; see Smartt et al. Reference Smartt, Eldridge, Crockett and Maund2009 and Smartt Reference Smartt2015)? This question is tightly connected to another, more fundamental one, namely: What are the conditions for an explosive runaway, and how do multi-dimensional effects modify them?
3.3.1 Conditions for runaway shock expansion
Even without the complications of multi-D fluid flow, the physics of shock revival is subtle. In spherical symmetry, one can show that for a given mass accretion rate
![]() $\dot{M}$
, there is a maximum (critical) electron-flavour luminosity L
ν at the neutrinosphere above which stationary accretion flow onto the proto-neutron star is no longer possible (Burrows & Goshy Reference Burrows and Goshy1993; cp. Section 2). This also holds true if the contribution of the accretion luminosity due to cooling outside the neutrinosphere is taken into account (Pejcha & Thompson Reference Pejcha and Thompson2012). The limit for the existence of stationary solutions does not perfectly coincide with the onset of runaway shock expansion, however. Using 1D light-bulb simulations (i.e., neglecting the contribution of the accretion luminosity), Fernández (Reference Fernández2012) and Gabay, Balberg, & Keshet (Reference Gabay, Balberg and Keshet2015) showed that the accretion flow becomes unstable to oscillatory and non-oscillatory instability slightly below the limit of Burrows & Goshy (Reference Burrows and Goshy1993). Moreover, it is unclear whether the negative feedback of shock expansion on the accretion luminosity and hence on the neutrino heating could push models into a limit cycle (cp. Figure 28 of Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a) even above the threshold for non-stationarity.
$\dot{M}$
, there is a maximum (critical) electron-flavour luminosity L
ν at the neutrinosphere above which stationary accretion flow onto the proto-neutron star is no longer possible (Burrows & Goshy Reference Burrows and Goshy1993; cp. Section 2). This also holds true if the contribution of the accretion luminosity due to cooling outside the neutrinosphere is taken into account (Pejcha & Thompson Reference Pejcha and Thompson2012). The limit for the existence of stationary solutions does not perfectly coincide with the onset of runaway shock expansion, however. Using 1D light-bulb simulations (i.e., neglecting the contribution of the accretion luminosity), Fernández (Reference Fernández2012) and Gabay, Balberg, & Keshet (Reference Gabay, Balberg and Keshet2015) showed that the accretion flow becomes unstable to oscillatory and non-oscillatory instability slightly below the limit of Burrows & Goshy (Reference Burrows and Goshy1993). Moreover, it is unclear whether the negative feedback of shock expansion on the accretion luminosity and hence on the neutrino heating could push models into a limit cycle (cp. Figure 28 of Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a) even above the threshold for non-stationarity.
Since an a priori prediction of the critical luminosity,
![]() $L_\nu (\dot{M})$
is not feasible, heuristic criteria have been developed (Janka & Keil Reference Janka, Keil, Labhardt, Binggeli and Buser1998; Janka, Kifonidis, & Rampp Reference Janka, Kifonidis, Rampp, Blaschke, Glendenning and Sedrakian2001; Thompson Reference Thompson2000; Thompson, Quataert, & Burrows Reference Thompson, Quataert and Burrows2005; Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008; Pejcha & Thompson Reference Pejcha and Thompson2012; Fernández Reference Fernández2012; Gabay et al. Reference Gabay, Balberg and Keshet2015; Murphy & Dolence Reference Murphy and Dolence2015) to gauge the proximity of numerical supernova models to an explosive runaway (rather than for pinpointing the formal onset of the runaway after the fact, which is of less interest). The most commonly used criticality parameters are based on the ratio of two relevant timescales for the gain region (Janka & Keil Reference Janka, Keil, Labhardt, Binggeli and Buser1998; Janka et al. Reference Janka, Kifonidis, Rampp, Blaschke, Glendenning and Sedrakian2001; Thompson Reference Thompson2000; Thompson et al. Reference Thompson, Quataert and Burrows2005; Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008), namely the advection or dwell time τadv that accreted material spends in the gain region, and the heating timescale τheat over which neutrino energy deposition changes the total or internal energy of the gain region appreciably. If τadv > τheat, neutrino heating can equalise the net binding energy of the accreted material before it is lost from the gain region, and one expects that the shock must expand significantly due to the concomitant increase in pressure. Since this expansion further increases τadv, an explosive runaway is likely to ensue.
$L_\nu (\dot{M})$
is not feasible, heuristic criteria have been developed (Janka & Keil Reference Janka, Keil, Labhardt, Binggeli and Buser1998; Janka, Kifonidis, & Rampp Reference Janka, Kifonidis, Rampp, Blaschke, Glendenning and Sedrakian2001; Thompson Reference Thompson2000; Thompson, Quataert, & Burrows Reference Thompson, Quataert and Burrows2005; Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008; Pejcha & Thompson Reference Pejcha and Thompson2012; Fernández Reference Fernández2012; Gabay et al. Reference Gabay, Balberg and Keshet2015; Murphy & Dolence Reference Murphy and Dolence2015) to gauge the proximity of numerical supernova models to an explosive runaway (rather than for pinpointing the formal onset of the runaway after the fact, which is of less interest). The most commonly used criticality parameters are based on the ratio of two relevant timescales for the gain region (Janka & Keil Reference Janka, Keil, Labhardt, Binggeli and Buser1998; Janka et al. Reference Janka, Kifonidis, Rampp, Blaschke, Glendenning and Sedrakian2001; Thompson Reference Thompson2000; Thompson et al. Reference Thompson, Quataert and Burrows2005; Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008), namely the advection or dwell time τadv that accreted material spends in the gain region, and the heating timescale τheat over which neutrino energy deposition changes the total or internal energy of the gain region appreciably. If τadv > τheat, neutrino heating can equalise the net binding energy of the accreted material before it is lost from the gain region, and one expects that the shock must expand significantly due to the concomitant increase in pressure. Since this expansion further increases τadv, an explosive runaway is likely to ensue.
The timescale criterion τadv/τheat > 1 has the virtue of being easy to evaluate since the two timescales can be defined in terms of global quantities such as the total energy E
tot, g in the gain region, the volume-integrated neutrino heating rate
![]() $\dot{Q}_\nu$
, and the mass M
g in the gain region (which can be used to define
$\dot{Q}_\nu$
, and the mass M
g in the gain region (which can be used to define
![]() $\tau _{\rm adv}=M_{\rm gain}/\dot{M}$
under steady-state conditions). The significance of these global quantities for the problem of shock revival is immediately intuitive, though care must be taken to define the heating timescale properly. Thompson (Reference Thompson2000), Thompson et al. (Reference Thompson, Quataert and Burrows2005), Murphy & Burrows (Reference Murphy and Burrows2008), and Pejcha & Thompson (Reference Pejcha and Thompson2012) define τheat as the timescale for changes in the internal energy E
int in the gain region:
$\tau _{\rm adv}=M_{\rm gain}/\dot{M}$
under steady-state conditions). The significance of these global quantities for the problem of shock revival is immediately intuitive, though care must be taken to define the heating timescale properly. Thompson (Reference Thompson2000), Thompson et al. (Reference Thompson, Quataert and Burrows2005), Murphy & Burrows (Reference Murphy and Burrows2008), and Pejcha & Thompson (Reference Pejcha and Thompson2012) define τheat as the timescale for changes in the internal energy E
int in the gain region:
based on the premise that shock expansion is regulated by the increase in pressure (and hence in internal energy). This definition yields unsatisfactory results, however. The criticality parameter can be spuriously low at shock revival if this definition is used (τadv/τheat < 0.4).
By defining τheat in terms of the total (internal+kinetic+potential) energyFootnote 6 of the gain region (Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b):
the criterion τadv/τheat > 1 becomes a very accurate predictor for non-oscillatory instability (Fernández Reference Fernández2012; Gabay et al. Reference Gabay, Balberg and Keshet2015). This indicates that the relevant energy scale to which the quasi-hydrostatic stratification of the post-shock region is the total energy (or perhaps the total or stagnation enthalpy) of the gain region, and not the internal energy. This is consistent with the observation that runaway shock expansion occurs roughly once the total energy or the Bernoulli integral (Fernández Reference Fernández2012; Burrows et al. Reference Burrows, Hayes and Fryxell1995) reach positive values somewhere (not everywhere) in the post-shock region, which is essentially what the timescale criterion estimates. What is crucial is that the density and pressure gradients between the gain radius and the shock (and hence the shock position) depends sensitively on the ratio of enthalpy h (or the internal energy) and the gravitational potential, rather than on enthalpy alone. Under the (justified) assumption that quadratic terms in
![]() $v_\text{r}^2$
in the momentum and energy equation are sufficiently small to be neglected in the post-shock region, one can show (see Appendix A) that the logarithmic derivative of the density ρ in the gain region is constrained by
$v_\text{r}^2$
in the momentum and energy equation are sufficiently small to be neglected in the post-shock region, one can show (see Appendix A) that the logarithmic derivative of the density ρ in the gain region is constrained by
where M is the proto-neutron star mass. Once h > GM/r or even e int > GM/r (where e int is the internal energy per unit mass), significant shock expansion must ensue due to the flattening of pressure and density gradients.
Janka (Reference Janka2012), Müller & Janka (Reference Müller and Janka2015), and Summa et al. (Reference Summa, Hanke, Janka, Melson, Marek and Müller2016) have also pointed out that the timescale criterion can be converted into a scaling law for the critical electron-flavour luminosity L
ν and mean energy E
ν in terms of the proto-neutron star mass M, the accretion rate
![]() $\dot{M}$
, and the gain radius r
g,
$\dot{M}$
, and the gain radius r
g,
The concept of the critical luminosity, the timescale criterion, and the condition of positive total energy or a positive Bernoulli parameter at the gain radius are thus intimately related and appear virtually interchangeable considering that they remain approximate criteria for runaway shock expansion anyway. This is also true for some other explosion criteria that have been proposed, e.g., the antesonic condition of Pejcha & Thompson (Reference Pejcha and Thompson2012), which states that the sound speed c s must exceed a certain fraction of the escape velocity v esc for runaway shock expansion somewhere in the accretion flow:
Approximating the equation of state as a radiation-dominated gas with an adiabatic index γ = 4/3 and a pressure of P = ρe int/3 = ρh/4, one finds that the antesonic condition roughly translates to
i.e., the internal energy and the enthalpy must be close to the gravitational binding energy (even if the precise critical values for e int and h may shift a bit for a realistic equation of state).Footnote 7
3.3.2 Impact of multi-D effects on the heating conditions
Why do multi-D effects bring models closer to shock revival, and how is this reflected in the aforementioned explosion criteria? Do these explosion criteria even remain applicable in multi-D in the first place?
The canonical interpretation has long been that the runaway condition τadv > τheat remains the decisive criterion in multi-D, and that multi-D effects facilitate shock revival mainly by increasing the advection time-scale τadv (Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008). Especially close to criticality, τheat is also shortened due to feedback processes—better heating conditions imply that the net binding energy in the gain region and hence τheat must decrease.
Whilst simulations clearly show increased advection timescales in multi-D compared to 1D (Buras et al. Reference Buras, Janka, Rampp and Kifonidis2006b; Murphy & Burrows Reference Murphy and Burrows2008; Hanke et al. Reference Hanke, Marek, Müller and Janka2012) as a result of larger shock radii, the underlying cause for larger accretion shock radii in multi-D is more difficult to pinpoint. Ever since the first 2D simulations, both the transport of neutrino-heated high-entropy material from the gain radius out to the shock (Herant et al. Reference Herant, Benz, Hix, Fryer and Colgate1994; Janka & Müller Reference Janka and Müller1996) as well as the ‘turbulent pressure’ of convective bubbles colliding with the shock (Burrows et al. Reference Burrows, Hayes and Fryxell1995) have been invoked to explain larger shock radii in multi-D. Both effects are plausible since they change the components P (thermal pressure) and ρv⊗v (where v is the velocity) of the momentum stress tensor that must balance the ram pressure upstream of the shock during stationary accretion.
That the turbulent pressure plays an important role follows already from the high turbulent Mach number
![]() $\mathord {{\sim }0.5}$
in the post-shock region (Burrows et al. Reference Burrows, Hayes and Fryxell1995; Müller et al. Reference Müller, Janka and Heger2012b) before the onset of shock revival, and has been demonstrated quantitatively by Murphy, Dolence, & Burrows (Reference Murphy, Dolence and Burrows2013) and Couch & Ott (Reference Couch and Ott2015) using spherical Reynolds decomposition to analyse parameterised 2D and 3D simulations. Using a simple estimate for the shock expansion due to turbulent pressure, Müller & Janka (Reference Müller and Janka2015) were even able to derive the reduction of the critical heating functional in multi-D compared to 1D in terms of the average squared turbulent Mach number ⟨Ma2⟩ in the gain region,
$\mathord {{\sim }0.5}$
in the post-shock region (Burrows et al. Reference Burrows, Hayes and Fryxell1995; Müller et al. Reference Müller, Janka and Heger2012b) before the onset of shock revival, and has been demonstrated quantitatively by Murphy, Dolence, & Burrows (Reference Murphy, Dolence and Burrows2013) and Couch & Ott (Reference Couch and Ott2015) using spherical Reynolds decomposition to analyse parameterised 2D and 3D simulations. Using a simple estimate for the shock expansion due to turbulent pressure, Müller & Janka (Reference Müller and Janka2015) were even able to derive the reduction of the critical heating functional in multi-D compared to 1D in terms of the average squared turbulent Mach number ⟨Ma2⟩ in the gain region,
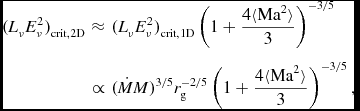 $$\begin{eqnarray}
(L_\nu E_\nu ^2)_{\rm crit,2D} &\approx & (L_\nu E_\nu ^2)_{\rm crit,1D} \left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5}\\
\nonumber &\propto & (\dot{M} M)^{3/5} r_{\rm g}^{-2/5} \left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5},
\end{eqnarray}$$
$$\begin{eqnarray}
(L_\nu E_\nu ^2)_{\rm crit,2D} &\approx & (L_\nu E_\nu ^2)_{\rm crit,1D} \left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5}\\
\nonumber &\propto & (\dot{M} M)^{3/5} r_{\rm g}^{-2/5} \left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5},
\end{eqnarray}$$
and then obtained (L ν E 2 ν)crit, 2D ≈ 0.75(L ν E 2 ν)crit, 1D in rough agreement with simulations using a model for the saturation of non-radial fluid motions (see Section 3.3.3).
Nonetheless, there is likely no monocausal explanation for better heating conditions in multi-D. Yamasaki & Yamada (Reference Yamasaki and Yamada2006) found, for example, that convective energy transport from the gain radius to the shock also reduces the critical luminosity (although they somewhat overestimated the effect by assuming constant entropy in the entire gain region). Convective energy transport reduces the slope of the pressure gradient between the gain radius (where the pressure is set by the neutrino luminosity and mean energy) and the shock, and thus pushes the shock out by increasing the thermal post-shock pressure. That this effect also plays a role alongside the turbulent pressure can be substantiated by an analysis of neutrino hydrodynamics simulations (Bollig et al. in preparation).
Only a detailed analysis of the properties of turbulence in the gain region (Murphy & Meakin Reference Murphy and Meakin2011) combined with a model for the interaction of turbulence with a non-spherical accretion shock will reveal the precise combination of multi-D effects that conspire to increase the shock radius compared to 1D. This is no prerequisite for understanding the impact of multi-D effects on the runaway condition as encapsulated by a phenomenological correction factor in Equation (13), since effects like turbulent energy transport, turbulent bulk viscosity, etc. will also scale with the square of the turbulent Mach number in the post-shock region just like the turbulent pressure. They are effectively lumped together in the correction factor (1 + 4/3⟨Ma2⟩)−3/5. The turbulent Mach number in the post-shock region is thus the crucial parameter for the reduction of the critical luminosity in multi-D, although the coefficient of ⟨Ma2⟩ still needs to be calibrated against multi-D simulations (and maybe different in 2D and 3D).
This does not imply, however, that the energetic requirements for runaway shock expansion in multi-D are fundamentally different from 1D: Runaway still occurs roughly once some material in the gain region first acquires positive total (internal+kinetic+potential) energy e tot; and the required energy input for this ultimately stems from neutrino heating.Footnote 8
3.3.3 Saturation of instabilities
What complicates the role of multi-D effects in the neutrino-driven mechanism is that the turbulent Mach number in the gain region itself depends on the heating conditions, which modify the growth rates and saturation properties of convection and the SASI. Considerable progress has been made in recent years in understanding this feedback mechanism and the saturation properties of these two instabilities.
The linear phases of convection and the SASI are now rather well understood. The growth rates for buoyancy-driven convective instability are expected to be of order of the Brunt–Väisälä frequency ωBV, which can be expressed in terms of P, ρ, c s, and the local gravitational acceleration g asFootnote 9
which becomes positive in the gain region due to neutrino heating. A first-order estimate yields
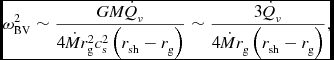 $$\begin{equation}
\omega _{\rm BV}^2 \sim \frac{G M \dot{Q}_\nu }{4\dot{M} r_{\rm g} ^2 c_{\rm s}^2 \left(r_{\rm sh}-r_{\rm g}\right)} \sim \frac{3\dot{Q}_\nu }{4\dot{M} r_{\rm g} \left(r_{\rm sh}-r_{\rm g}\right)},
\end{equation}$$
$$\begin{equation}
\omega _{\rm BV}^2 \sim \frac{G M \dot{Q}_\nu }{4\dot{M} r_{\rm g} ^2 c_{\rm s}^2 \left(r_{\rm sh}-r_{\rm g}\right)} \sim \frac{3\dot{Q}_\nu }{4\dot{M} r_{\rm g} \left(r_{\rm sh}-r_{\rm g}\right)},
\end{equation}$$
using c 2 s ≈ GM/(3r g) at the gain radius (cp. Müller & Janka Reference Müller and Janka2015). An important subtlety is that advection can stabilise the flow so that ω2 BV > 0 is no longer sufficient for instability unless large seed perturbations in density are already present. Instability instead depends on the more restrictive criterion for the parameter χ (Foglizzo et al. Reference Foglizzo, Scheck and Janka2006):
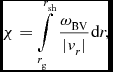 $$\begin{equation}
\chi = \int \limits _{r_{\rm g}}^{r_{\rm sh}}\frac{\omega _{\rm BV}}{|v_r|}{\rm d}r,
\end{equation}$$
$$\begin{equation}
\chi = \int \limits _{r_{\rm g}}^{r_{\rm sh}}\frac{\omega _{\rm BV}}{|v_r|}{\rm d}r,
\end{equation}$$
with χ ≳ 3 indicating convective instability.
The scaling of the linear growth rate ωSASI of SASI modes is more complicated, since it involves both the duration τcyc of the underlying advective-acoustic cycle as well as a quality factor
![]() $\mathcal {Q}$
for the conversion of vorticity and entropy perturbations into acoustic perturbation in the deceleration region below the gain region and the reverse process at the shock (Foglizzo et al. Reference Foglizzo, Scheck and Janka2006, Reference Foglizzo, Galletti, Scheck and Janka2007):
$\mathcal {Q}$
for the conversion of vorticity and entropy perturbations into acoustic perturbation in the deceleration region below the gain region and the reverse process at the shock (Foglizzo et al. Reference Foglizzo, Scheck and Janka2006, Reference Foglizzo, Galletti, Scheck and Janka2007):
For realistic models with strong SASI, one finds
![]() $\ln |\mathcal {Q}| \sim 2$
(Scheck et al. Reference Scheck, Janka, Foglizzo and Kifonidis2008; Müller et al. Reference Müller, Janka and Heger2012b). SASI growth appears to be suppressed for χ ≳ 3 probably because convection destroys the coherence of the waves involved in the advective-acoustic cycle (Guilet et al. Reference Guilet, Sato and Foglizzo2010). Interestingly, the demarcation line χ = 3 between the SASI- and convection-dominated regimes is also valid in the non-linear regime if χ is computed from the angle- and time-averaged mean flow (Fernández Reference Fernández2012); and both the SASI and convection appear to drive χ close to this critical value (Fernández Reference Fernández2012).
$\ln |\mathcal {Q}| \sim 2$
(Scheck et al. Reference Scheck, Janka, Foglizzo and Kifonidis2008; Müller et al. Reference Müller, Janka and Heger2012b). SASI growth appears to be suppressed for χ ≳ 3 probably because convection destroys the coherence of the waves involved in the advective-acoustic cycle (Guilet et al. Reference Guilet, Sato and Foglizzo2010). Interestingly, the demarcation line χ = 3 between the SASI- and convection-dominated regimes is also valid in the non-linear regime if χ is computed from the angle- and time-averaged mean flow (Fernández Reference Fernández2012); and both the SASI and convection appear to drive χ close to this critical value (Fernández Reference Fernández2012).
Both in the SASI-dominated regime and the convection-dominated regime, large growth rates are observed in simulations. It only takes a few tens of milliseconds until the instabilities reach their saturation amplitudes. For this reason, the turbulent Mach number and the beneficial effect of multi-D effects on the heating conditions are typically more sensitive to the saturation mechanism than to initial conditions, so that the onset of shock revival is only subject to modest stochastic variations (Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016). Exceptions apply when the heating conditions vary rapidly, e.g., due to the infall of a shell interface or extreme variations in shock radius (as in the light-bulb models of Cardall & Budiardja Reference Cardall and Budiardja2015), and the runaway condition is only narrowly met or missed (Melson et al. Reference Melson, Janka and Marek2015a; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016).
The saturation properties of convection were clarified by Murphy et al. (Reference Murphy, Dolence and Burrows2013), who determined that the volume-integrated neutrino heating rate
![]() $\dot{Q}_\nu$
and the convective luminosity L
conv in the gain region roughly balance each other. This can be understood as the result of a self-adjustment process of the accretion flow, whereby a marginally stable, quasi-stationary stratification with χ ≈ 3 is established (Fernández Reference Fernández2012). Müller & Janka (Reference Müller and Janka2015) showed that this can be translated into a scaling law that relates the average mass-specific neutrino heating rate
$\dot{Q}_\nu$
and the convective luminosity L
conv in the gain region roughly balance each other. This can be understood as the result of a self-adjustment process of the accretion flow, whereby a marginally stable, quasi-stationary stratification with χ ≈ 3 is established (Fernández Reference Fernández2012). Müller & Janka (Reference Müller and Janka2015) showed that this can be translated into a scaling law that relates the average mass-specific neutrino heating rate
![]() $\dot{q}_\nu$
in the gain region to the root mean square average δv of non-radial velocity fluctuations:
$\dot{q}_\nu$
in the gain region to the root mean square average δv of non-radial velocity fluctuations:
That a similar scaling should apply in the SASI-dominated regime is not immediately intuitive. Müller & Janka (Reference Müller and Janka2015) in fact tested Equation (18) using a SASI-dominated 2D model and argued that self-adjustment of the flow to χ ≈ 3 will result in the same scaling law as for convection-dominated models. However, models suggest that a different mechanism may be at play in the SASI-dominated regime. Simulations are at least equally compatible with the mechanism proposed by Guilet et al. (Reference Guilet, Sato and Foglizzo2010), who suggested that saturation of the SASI is mediated by parasitic instabilities and occurs once the growth rate of the parasite equals the growth rate of the SASI: Assuming that the Kelvin–Helmholtz instability is the dominant parasite, a simple order-of-magnitude estimate for saturation can be obtained by equating ωSASI and the average shear rate:
where Λ is the effective width of the shear layer. Kazeroni, Guilet, & Foglizzo (Reference Kazeroni, Guilet and Foglizzo2016) find that the Kelvin–Helmholtz instability operates primarily in directions where the shock radius is larger, which suggests Λ = r
sh, max − r
g. This results in a scaling law that relates the velocity fluctuations to the average radial velocity
![]() $\langle v_\text{r} \rangle$
in the gain region:
$\langle v_\text{r} \rangle$
in the gain region:
where we assumed τcyc ≈ τadv. The quality factor
![]() $\mathcal {Q}$
can in principle change significantly with time and between different models. Nonetheless, together with the assumption of a roughly constant quality factor, Equation (20) appears to capture the dynamics of the SASI in 3D quite well for a simulation of an
$\mathcal {Q}$
can in principle change significantly with time and between different models. Nonetheless, together with the assumption of a roughly constant quality factor, Equation (20) appears to capture the dynamics of the SASI in 3D quite well for a simulation of an
![]() $18\,\text{M}_\odot$
progenitor with the coconut-fmt code (Müller & Janka Reference Müller and Janka2015) as illustrated in Figure 4.
$18\,\text{M}_\odot$
progenitor with the coconut-fmt code (Müller & Janka Reference Müller and Janka2015) as illustrated in Figure 4.

Figure 4. Comparison of the root-mean-square average δv of non-radial velocity component in the gain region (black) with two phenomenological models for the saturation of non-radial instabilities in a SASI-dominated 3D model of an
![]() $18\,\text{M}_\odot$
star using the coconut-fmt code. The red curve shows an estimate based on Equation (18), which rests on the assumption of a balance between buoyant driving and turbulent dissipation (Murphy et al. Reference Murphy, Dolence and Burrows2013; Müller & Janka Reference Müller and Janka2015). The blue curve shows the prediction of Equation (20), which assumes that saturation is regulated by a balance between the growth rate of the SASI and parasitic Kelvin–Helmholtz instabilities (Guilet, Sato, & Foglizzo Reference Guilet, Sato and Foglizzo2010). Even though Equation (20) assumes a constant quality factor
$18\,\text{M}_\odot$
star using the coconut-fmt code. The red curve shows an estimate based on Equation (18), which rests on the assumption of a balance between buoyant driving and turbulent dissipation (Murphy et al. Reference Murphy, Dolence and Burrows2013; Müller & Janka Reference Müller and Janka2015). The blue curve shows the prediction of Equation (20), which assumes that saturation is regulated by a balance between the growth rate of the SASI and parasitic Kelvin–Helmholtz instabilities (Guilet, Sato, & Foglizzo Reference Guilet, Sato and Foglizzo2010). Even though Equation (20) assumes a constant quality factor
![]() $|\mathcal {Q}|$
to estimate the SASI growth rate, it appears to provide a good estimate for the dynamics of the model. Interestingly, the saturation models for the SASI- and convection dominated regimes give similar results during later phases even though the mechanism behind the driving instability is completely different.
$|\mathcal {Q}|$
to estimate the SASI growth rate, it appears to provide a good estimate for the dynamics of the model. Interestingly, the saturation models for the SASI- and convection dominated regimes give similar results during later phases even though the mechanism behind the driving instability is completely different.
Equation (18) for the convection-dominated regime and Equation (20) apparently predict turbulent Mach numbers in the same ballpark. This can be understood by expressing
![]() $\dot{q}_\nu$
in terms of the accretion efficiency
$\dot{q}_\nu$
in terms of the accretion efficiency
![]() $\eta _{\rm acc} =L_\nu /(GM \dot{M}/r_{\rm g})$
and the heating efficiency
$\eta _{\rm acc} =L_\nu /(GM \dot{M}/r_{\rm g})$
and the heating efficiency
![]() $\eta _{\rm heat} =\dot{Q}_\nu /L_\nu$
:
$\eta _{\rm heat} =\dot{Q}_\nu /L_\nu$
:
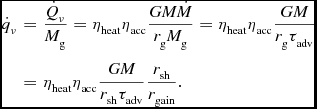 $$\begin{eqnarray}
\dot{q}_\nu &=&\frac{\dot{Q}_\nu }{M_{\rm g}}= \eta _{\rm heat} \eta _{\rm acc} \frac{GM \dot{M}}{r_{\rm g} M_{\rm g}}= \eta _{\rm heat} \eta _{\rm acc} \frac{GM}{r_{\rm g} \tau _{\rm adv}} \\
\nonumber &=& \eta _{\rm heat} \eta _{\rm acc} \frac{GM}{r_{\rm sh} \tau _{\rm adv}}\frac{r_{\rm sh}}{r_{\rm gain}}.
\end{eqnarray}$$
$$\begin{eqnarray}
\dot{q}_\nu &=&\frac{\dot{Q}_\nu }{M_{\rm g}}= \eta _{\rm heat} \eta _{\rm acc} \frac{GM \dot{M}}{r_{\rm g} M_{\rm g}}= \eta _{\rm heat} \eta _{\rm acc} \frac{GM}{r_{\rm g} \tau _{\rm adv}} \\
\nonumber &=& \eta _{\rm heat} \eta _{\rm acc} \frac{GM}{r_{\rm sh} \tau _{\rm adv}}\frac{r_{\rm sh}}{r_{\rm gain}}.
\end{eqnarray}$$
If we neglect the ratio r
sh/r
g and approximate the average post-shock velocity as
![]() $| \langle v_{\rm r} \rangle | \approx \beta ^{-1} \sqrt{GM/r_{\rm sh}}$
(where β is the compression ratio in the shock), we obtain
$| \langle v_{\rm r} \rangle | \approx \beta ^{-1} \sqrt{GM/r_{\rm sh}}$
(where β is the compression ratio in the shock), we obtain
and hence
For plausible values (e.g., ηheat = 0.05ηacc = 2, β = 10), one finds
![]() $\delta v \sim 2 |\langle v_\text{r} \rangle |$
, i.e., the turbulent Mach number at saturation is of the same order of magnitude in the convection- and SASI-dominated regimes (where at least
$\delta v \sim 2 |\langle v_\text{r} \rangle |$
, i.e., the turbulent Mach number at saturation is of the same order of magnitude in the convection- and SASI-dominated regimes (where at least
![]() $\ln |\mathcal {Q}| \mathord {\sim } 2$
can be reached).
$\ln |\mathcal {Q}| \mathord {\sim } 2$
can be reached).
Equations (18) and (20) remain order-of-magnitude estimates; and either of the instabilities may be more efficient at pumping energy into non-radial turbulent motions in the gain region, as suggested by the light-bulb models of Fernández (Reference Fernández2015) and Cardall & Budiardja (Reference Cardall and Budiardja2015). These authors find that the SASI can lower the critical luminosity in 3D considerably further than convection. Fernández (Reference Fernández2010) attributes this to the emergence of the spiral mode of the SASI (Blondin & Mezzacappa Reference Blondin and Mezzacappa2007; Fernández Reference Fernández2010) in 3D, which can store more non-radial kinetic energy than the SASI sloshing mode in 2D, but this has yet to be borne out by self-consistent neutrino hydrodynamics simulations (see Section 3.4 for further discussion).
3.3.4 Why do models explode more easily in 2D than in 3D?
How can one explain the different behaviour of 2D and 3D models in the light of our current understanding of the interplay between neutrino heating, convection, and the SASI? It seems fair to say that we can presently only offer a heuristic interpretation for the more pessimistic evolution of 3D models.
The most glaring difference between 2D and 3D models (especially in the convection-dominated regime) prior to shock revival lies in the typical scale of the turbulent structures, which are smaller in 3D (Hanke et al. Reference Hanke, Marek, Müller and Janka2012; Couch Reference Couch2013b; Couch & Ott Reference Couch and Ott2015), whereas the inverse turbulent cascade in 2D (Kraichnan Reference Kraichnan1967) artificially channels turbulent kinetic energy to large scales. This implies that the effective dissipation length (or also the effective mixing length for energy transport) are smaller in 3D, so that smaller dimensionless coefficients C appear in relations like Equation (18),
and the turbulent Mach number will be smaller for a given neutrino heating rate. Indeed, for the
![]() $18\,\text{M}_\odot$
model shown in Figure 4, we find
$18\,\text{M}_\odot$
model shown in Figure 4, we find
in 3D rather than what Müller & Janka (Reference Müller and Janka2015) inferred from 2D models (admittedly using a different progenitor),
Following the arguments of Müller & Janka (Reference Müller and Janka2015) to infer the correction factor
![]() $\left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5}$
for multi-D effects in Equation (13), one would then expect a considerably larger critical luminosity in 3D, i.e., (L
ν
E
2
ν)crit, 3D ≈ 0.85(L
ν
E
2
ν)crit, 1D instead of (L
ν
E
2
ν)crit, 2D ≈ 0.75(L
ν
E
2
ν)crit, 1D in 2D.
$\left(1+\frac{4\langle {\rm Ma}^2 \rangle }{3}\right)^{-3/5}$
for multi-D effects in Equation (13), one would then expect a considerably larger critical luminosity in 3D, i.e., (L
ν
E
2
ν)crit, 3D ≈ 0.85(L
ν
E
2
ν)crit, 1D instead of (L
ν
E
2
ν)crit, 2D ≈ 0.75(L
ν
E
2
ν)crit, 1D in 2D.
Such a large difference in the critical luminosity does not tally with the findings of light-bulb models that show that the critical luminosities in 2D and 3D are still very close to each other. This already indicates that more subtle effects may be at play in 3D that almost compensate the stronger effective dissipation of turbulent motions. The fact that simulations typically show transient phases of stronger shock expansion and more optimistic heating conditions in 3D than in 2D (Hanke et al. Reference Hanke, Marek, Müller and Janka2012; Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) also points in this direction.
Furthermore, light-bulb models (Handy, Plewa, & Odrzywołek Reference Handy, Plewa and Odrzywołek2014) and multi-group neutrino hydrodynamics simulations (Melson et al. Reference Melson, Janka and Marek2015a; Müller Reference Müller2015) have demonstrated that favourable 3D effects come into play after shock revival. These works showed that 3D effects can lead to a faster, more robust growth of the explosion energy provided that shock revival can be achieved in the first place.
The favourable 3D effects that are responsible for this may already counterbalance the adverse effect of stronger dissipation in the pre-explosion phase to some extent: Energy leakage from the gain region by the excitation of g-modes is suppressed in 3D because the forward turbulent cascade (Melson et al. Reference Melson, Janka and Marek2015a) and (at high Mach number) the more efficient growth of the Kelvin–Helmholtz instability (Müller Reference Müller2015) brake the downflows before they penetrate the convectively stable cooling layer. Moreover, the non-linear growth of the Rayleigh–Taylor instability is faster for three-dimensional plume-like structures than for 2D structures with planar (Yabe, Hoshino, & Tsuchiya Reference Yabe, Hoshino and Tsuchiya1991; Hecht et al. Reference Hecht, Ofer, Alon, Shvarts, Orszag and McCrory1995; Marinak et al. Reference Marinak1995) or toroidal geometry (as in the context of Rayleigh–Taylor mixing in the stellar envelope during the explosion phase; Kane et al. Reference Kane, Arnett, Remington, Glendinning, Müller, Fryxell and Teyssier2000; Hammer, Janka, & Müller Reference Hammer, Janka and Müller2010), which might explain why 3D models initially respond more strongly to sudden drops in the accretion rate at shell interfaces and exhibit better heating conditions than their 2D counterparts for brief periods. Finally, the difference in the effective dissipation length in 3D and 2D that is reflected by Equations (25) and (26) may not be universal and depend, e.g., on the heating conditions or the χ-parameter; the results of Fernández (Reference Fernández2015) in fact demonstrate that under appropriate circumstances more energy can be stored in non-radial motions in 3D than in 2D in the SASI-dominated regime.
3.4 Outlook: Classical ideas for more robust explosions
The existence of several competing—favourable and unfavourable—effects in 3D first-principle models does not change the fundamental fact that they remain more reluctant to explode than their 2D counterparts. This suggests that some important physical ingredient are still lacking in current simulations. Several avenues towards more robust explosion models have recently been explored. Some of the proposed solutions have a longer pedigree and revisit ideas (rapid rotation in supernova cores, enhanced neutrino luminosities) that have been investigated on and off in supernova theory already before the advent of 3D simulations. The more ‘radical’ solution of invoking strong seed perturbations from convective shell burning to boost non-radial instabilities in the post-shock region will be discussed separately in Section 5.
3.4.1 Rotation and beyond
Nakamura et al. (Reference Nakamura, Kuroda, Takiwaki and Kotake2014) and Janka et al. (Reference Janka, Melson and Summa2016) pointed out that rapid progenitor rotation can facilitate explosions in 3D. Janka et al. (Reference Janka, Melson and Summa2016) ascribed this partly to the reduction of the pre-shock infall velocity due to centrifugal forces, which decreases the ram pressure ahead of the shock. Even more importantly, rotational support also decreases the net binding energy |e tot| per unit mass in the gain region in their models. They derived an analytic correction factor for the critical luminosity in terms of the average-specific angular momentum j in the infalling shells:
Assuming rapid rotation with j ≫ 1016 cm2 s−1, one can obtain a significant reduction of the critical luminosity by several 10% as Janka et al. (Reference Janka, Melson and Summa2016) tested in a simulation with a modified rotation profile.Footnote 10 For very rapid rotation, other explosion mechanisms also become feasible, such as the magnetorotational mechanism (Akiyama et al. Reference Akiyama, Wheeler, Meier, Lichtenstadt, Meier and Lichtenstadt2003; Burrows et al. Reference Burrows, Dessart, Livne, Immler, Weiler and McCray2007b; Winteler et al. Reference Winteler, Käppeli, Perego, Arcones, Vasset, Nishimura, Liebendörfer and Thielemann2012; Mösta et al. Reference Mösta2014), or explosions driven by the low-T/W spiral instability (Takiwaki, Kotake, & Suwa Reference Takiwaki, Kotake and Suwa2016).
However, current stellar evolution models do not predict the required rapid rotation rates for these scenarios for the generic progenitors of type IIP supernovae. The typical specific angular momentum at a mass coordinate of
![]() $m=1.5\,\text{M}_\odot$
is only of the order of j ~ 1015 cm2 s−1 in models (Heger, Woosley, & Spruit Reference Heger, Woosley and Spruit2005) that include angular momentum transport by magnetic fields generated by the Tayler–Spruit dynamo (Spruit Reference Spruit2002), and asteroseismic measurements of core rotation in evolved low-mass stars suggest that the spin-down of the cores may be even more efficient (Cantiello et al. Reference Cantiello, Mankovich, Bildsten, Christensen-Dalsgaard and Paxton2014). For such slow rotation, centrifugal forces are negligible; Equation (27) suggests a change of the critical luminosity on the per-mil level. Neither is rotation expected to affect the character of neutrino-driven convection appreciably because the angular velocity Ω in the gain region is too small. The Rossby number is well above unity:
$m=1.5\,\text{M}_\odot$
is only of the order of j ~ 1015 cm2 s−1 in models (Heger, Woosley, & Spruit Reference Heger, Woosley and Spruit2005) that include angular momentum transport by magnetic fields generated by the Tayler–Spruit dynamo (Spruit Reference Spruit2002), and asteroseismic measurements of core rotation in evolved low-mass stars suggest that the spin-down of the cores may be even more efficient (Cantiello et al. Reference Cantiello, Mankovich, Bildsten, Christensen-Dalsgaard and Paxton2014). For such slow rotation, centrifugal forces are negligible; Equation (27) suggests a change of the critical luminosity on the per-mil level. Neither is rotation expected to affect the character of neutrino-driven convection appreciably because the angular velocity Ω in the gain region is too small. The Rossby number is well above unity:
assuming typical values of τadv ~ 10 ms and r sh ~ 100 km.
Magnetic field amplification by a small-scale dynamo or the SASI (Endeve, Cardall, & Budiardja Mezzacappa Reference Endeve, Cardall and Mezzacappa2010; Endeve et al. Reference Endeve, Cardall, Budiardja, Beck, Toedte, Mezzacappa and Blondin2012) could also help to facilitate shock revival with magnetic fields acting as a subsidiary to neutrino heating but without directly powering the explosion as in the magnetorototational mechanism. The 2D simulations of Obergaulinger et al. (Reference Obergaulinger, Janka and Aloy2014) demonstrated that magnetic fields can help organise the flow into large-scale modes and thereby allow earlier explosions, though the required initial field strengths for this are higher (
![]() $\mathord {\sim } 10^{12} \, {\rm G}$
) than the typical values predicted by stellar evolution models.
$\mathord {\sim } 10^{12} \, {\rm G}$
) than the typical values predicted by stellar evolution models.
3.4.2 Higher neutrino luminosities and mean energies?
Another possible solution for the problem of missing or delayed explosions in 3D lies in increasing the electron flavour luminosity and mean energy. This is intuitive from Equation (13), where a mere change of
![]() $\mathord {\sim }5\%$
in both L
ν and E
ν results in a net effect of 16%, which is almost on par with multi-D effects.
$\mathord {\sim }5\%$
in both L
ν and E
ν results in a net effect of 16%, which is almost on par with multi-D effects.
The neutrino luminosity is directly sensitive to the neutrino opacities, which necessitates precision modelling in order to capture shock propagation and heating correctly (Lentz et al. Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012a, Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012b; Müller et al. Reference Müller, Janka and Marek2012a; see also Section 4), as well as to other physical ingredients of the CCSN problem that influence the contraction of the proto-neutron star, such as general relativity and the nuclear equation of state (Janka Reference Janka2012; Müller et al. Reference Müller, Janka and Marek2012a; Couch Reference Couch2013a; Suwa et al. Reference Suwa, Takiwaki, Kotake, Fischer, Liebendörfer and Sato2013; O’Connor & Couch Reference O’Connor and Couch2015). Often such changes to the neutrino emission come with counterbalancing side effects (Mazurek’s law); e.g., stronger neutron star contraction will result in higher neutrino luminosities and mean energies, but will also result in a more tightly bound gain region, which necessitates stronger heating to achieve shock revival.
That the lingering uncertainties in the microphysics may nonetheless hold the key to more robust explosions has long been recognised in the case of the equation of state. Melson et al. (Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) pointed out that missing physics in our treatment of neutrino-matter interactions may equally well be an important part of the solution of the problem shock revival. Exploring corrections to neutral-current scattering cross-section due to the ‘strangeness’ of the nucleon, they found that changes in the neutrino cross-section on the level of a few 10% were sufficient to tilt the balance in favour of explosion for a
![]() $20\,\text{M}_\odot$
progenitor. Whilst Melson et al. (Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) deliberately assumed a larger value for the contribution of strange quarks to the axial form factor of the nucleon than currently measured (Airapetian et al. Reference Airapetian, Akopov, Akopov, Andrus, Aschenauer, Augustyniak and Avakian2007), the deeper significance of their result is that Mazurek’s law can sometimes be circumvented so that modest changes in the neutrino opacities still exert an appreciable effect on supernova dynamics. A re-investigation of the rates currently employed in the best supernova models for the (more uncertain) neutrino interaction processes that depend strongly on in-medium effects (charged-current absorption/emission, neutral current scattering, Bremsstrahlung; Burrows & Sawyer Reference Burrows and Sawyer1998, Reference Burrows and Sawyer1999; Reddy et al. Reference Reddy, Prakash, Lattimer and Pons1999; Hannestad & Raffelt Reference Hannestad and Raffelt1998) may thus be worthwhile (see Bartl, Pethick, & Schwenk Reference Bartl, Pethick and Schwenk2014; Rrapaj et al. Reference Rrapaj, Holt, Bartl, Reddy and Schwenk2015; Shen & Reddy Reference Shen and Reddy2014 for some recent efforts).
$20\,\text{M}_\odot$
progenitor. Whilst Melson et al. (Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b) deliberately assumed a larger value for the contribution of strange quarks to the axial form factor of the nucleon than currently measured (Airapetian et al. Reference Airapetian, Akopov, Akopov, Andrus, Aschenauer, Augustyniak and Avakian2007), the deeper significance of their result is that Mazurek’s law can sometimes be circumvented so that modest changes in the neutrino opacities still exert an appreciable effect on supernova dynamics. A re-investigation of the rates currently employed in the best supernova models for the (more uncertain) neutrino interaction processes that depend strongly on in-medium effects (charged-current absorption/emission, neutral current scattering, Bremsstrahlung; Burrows & Sawyer Reference Burrows and Sawyer1998, Reference Burrows and Sawyer1999; Reddy et al. Reference Reddy, Prakash, Lattimer and Pons1999; Hannestad & Raffelt Reference Hannestad and Raffelt1998) may thus be worthwhile (see Bartl, Pethick, & Schwenk Reference Bartl, Pethick and Schwenk2014; Rrapaj et al. Reference Rrapaj, Holt, Bartl, Reddy and Schwenk2015; Shen & Reddy Reference Shen and Reddy2014 for some recent efforts).
4 ASSESSMENT OF SIMULATION METHODOLOGY
Considering what has been pointed out in Section 3—the crucial role of hydrodynamic instabilities and the delicate sensitivity of shock revival to the neutrino luminosities and mean energies—it is natural to ask: What are the requirements for modelling the interplay of the different ingredients of the neutrino-driven mechanism accurately? This question is even more pertinent considering that the enormous expansion of the field during the recent years has sometimes produced contradictory results, debates about the relative importance of physical effects, and controversies about the appropriateness of certain simulation methodologies.
Ultimately, only the continuous evolution of the simulation codes, the inclusion of similar physics by different groups, and carefully designed cross-comparisons will eventually produce a ‘concordance model’ of the neutrino-driven mechanism and confirm that simulation results are robust against uncertainties. For 1D neutrino hydrodynamics simulations, this has largely been achieved in the wake of the pioneering comparison paper of Liebendörfer et al. (Reference Liebendörfer, Rampp, Janka and Mezzacappa2005), which has served as reference for subsequent method papers and sensitivity studies in 1D (Müller et al. Reference Müller, Janka and Dimmelmeier2010; Lentz et al. Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012a, Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012b; O’Connor Reference O’Connor2015; Just et al. Reference Just, Obergaulinger and Janka2015; Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016). Similar results of the Garching-QUB collaboration (Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016) and O’Connor & Couch (Reference O’Connor and Couch2015) with multi-group neutrino transport indicate a trend to a similar convergence in 2D, and more detailed comparisons are underway (see, e.g., https://www.authorea.com/users/1943/articles/97450/_show_article for efforts coordinated by E. O’Connor). Along the road to convergence, it appears useful to provide a preliminary review of some issues concerning the accuracy and reliability of supernova simulations.
4.1 Hydrodynamics
Recently, the discussion of the fidelity of the simulations has strongly focussed on the hydrodynamic side of the problem. As detailed in Section 3, multi-D effects play a crucial role in the explosion mechanism, and are regulated by a balance of driving (by neutrino heating through buoyancy, or by an inherent instability of the flow like the SASI) and dissipation.
4.1.1 Turbulence in supernova simulations
This balance needs to be modelled with sufficient physical and numerical accuracy. On the numerical side, the challenge consists in the turbulent high-Reynolds number flow, and the question arises to what extent simulations with relatively coarse resolution can capture this turbulent flow accurately. Various authors (Handy et al. Reference Handy, Plewa and Odrzywołek2014; Abdikamalov et al. Reference Abdikamalov2015; Radice, Couch, & Ott Reference Radice, Couch and Ott2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016) have stressed that the regime of fully developed turbulence cannot be reached with the limited resolution affordable to cover the gain region (
![]() $\mathord {\sim } 100$
zones, or even less) in typical models, and Handy et al. (Reference Handy, Plewa and Odrzywołek2014) thus prefer to speak of ‘perturbed laminar flow’ in simulations. Attempts to quantify the effective Reynolds number of the flow using velocity structure functions and spectral properties of the post-shock turbulence (Handy et al. Reference Handy, Plewa and Odrzywołek2014; Abdikamalov et al. Reference Abdikamalov2015; Radice et al. Reference Radice, Couch and Ott2015) put it at a few hundred at best, and sometimes even below 100.
$\mathord {\sim } 100$
zones, or even less) in typical models, and Handy et al. (Reference Handy, Plewa and Odrzywołek2014) thus prefer to speak of ‘perturbed laminar flow’ in simulations. Attempts to quantify the effective Reynolds number of the flow using velocity structure functions and spectral properties of the post-shock turbulence (Handy et al. Reference Handy, Plewa and Odrzywołek2014; Abdikamalov et al. Reference Abdikamalov2015; Radice et al. Reference Radice, Couch and Ott2015) put it at a few hundred at best, and sometimes even below 100.
This is in line with rule-of-thumb estimates based on the numerical diffusivity for the highest wavenumber (odd-even) modes in Godunov-based schemes as used in many supernova codes. This diffusivity can be calculated analytically (Appendix D of Müller Reference Müller2009; see also Arnett & Meakin Reference Arnett and Meakin2016 for a simpler estimate). For Riemann solvers that take all the wave families into account (e.g., Colella & Glaz Reference Colella and Glaz1985; Toro, Spruce, & Speares Reference Toro, Spruce and Speares1994; Mignone & Bodo Reference Mignone and Bodo2005; Donat & Marquina Reference Donat and Marquina1996), the numerical kinematic viscosity νnum in the subsonic regime is roughly given in terms of the typical velocity jump per cell δv gs and the cell width δl as νnum ~ δl δv gs. Relating δv gs to the turbulent velocity v and scale l of the largest eddy as δv gs ~ v(δl/l)1/3 (i.e., assuming Kolmogorov scaling) yields a numerical Reynolds number of
where N is the number of zones covering the largest eddy scale. For more diffusive solvers like HLLE (Einfeldt Reference Einfeldt1988), one obtains νnum ~ δl c s ~ δl v Ma−1 instead and
i.e., such solvers are strongly inferior for subsonic flow with low Mach number Ma.
Such coarse estimates are to be taken with caution, however. The numerical dissipation is non-linear and self-regulated as typical of implicit large-eddy simulations (ILES, Boris et al. Reference Boris, Grinstein, Oran and Kolbe1992; Grinstein, Margolin, & Rider Reference Grinstein, Margolin and Rider2007). In fact, the estimates already demonstrate that simply comparing the resolution in codes with different solvers and grid geometries can be misleading. Codes with three-wave solvers like Vertex-Prometheus (Rampp & Janka Reference Rampp and Janka2002; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a) and coconut-fmt (Müller & Janka Reference Müller and Janka2015) of the MPA-QUB collaboration, flash (Fryxell et al. Reference Fryxell2000) as used in Couch (Reference Couch2013a) and subsequent work by S. Couch and E. O’Connor, and the vh-1 hydro module (Blondin, Stevens, & Kallman Reference Blondin, Stevens and Kallman1991) in the Chimera code of the Oak Ridge-Florida Atlantic-NC State collaboration, have less stringent resolution requirements than HLLE-based codes (Ott et al. Reference Ott2012; Kuroda, Kotake, & Takiwaki Reference Kuroda, Kotake and Takiwaki2012). The reconstruction method, special tweaks for hydrostatic equilibrium (or an the lack of such a treatment), as well as the grid geometry and grid-induced perturbations (Janka et al. Reference Janka, Melson and Summa2016; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016) also affect the behaviour and resolution-dependence of the simulated turbulence.
4.1.2 Resolution requirements—a critical assessment
Regardless of the employed numerical schemes, the fact remains that the achievable numerical Reynolds number in supernova simulations is limited, and that the regime of fully developed turbulence (Re ≫ 1000) will not be achieved in the near future, as it would require ≳ 512 radial zones in the gain region alone. The question for supernova models, however, is not whether all the facets of turbulence in inviscid flow can be reproduced, but whether the flow properties that matter for the neutrino-driven mechanism are computed with sufficient accuracy. In fact, one cannot even hope that simply cranking up the numerical resolution with ILES methods would give the correct solution: In reality, non-ideal effects such as neutrino viscosity and drag (van den Horn & van Weert Reference van den Horn and van Weert1984; Burrows Reference Burrows1988; Jedamzik, Katalinić, & Olinto Reference Jedamzik, Katalinić and Olinto1998; Guilet, Müller, & Janka Reference Guilet, Müller and Janka2015) come into play, and deviations of the turbulent Prandtl number from unity as well as MHD effects like a small-scale dynamo (see Section 3.4) can complicate the picture even for non-rotating, weakly magnetised supernova cores. These effects will likely not grossly alter the dynamics of convection and the SASI, but the physical reality may be slightly different from the limit of infinite resolution if these effects are not accounted for and inviscid flow is assumed instead.
At the end of the day, these additional complications and the finite resolution probably have a limited effect on supernova dynamics, since they only affect a correction term to the critical luminosity such as (1 + 4/3⟨Ma2⟩)−3/5 in Equation (13) through the effective dissipation length that determines the non-dimensional coefficient in Equation (18). If we repeat the analytic estimate for L crit of Müller & Janka (Reference Müller and Janka2015), but assume stronger dissipation and decrease their critical Mach number at shock revival Ma2 crit = 0.4649 by 10%, then Equation (13) suggests an increase of the critical luminosity from 74.9% of the 1D value to of 76.6% of the 1D value, which is a minute change. Modelling turbulent dissipation within 10% uncertainty thus seems wholly sufficient given that one can hardly hope to achieve 1% accuracy for the neutrino luminosities and mean energies.
The turbulent dissipation does not change without bounds with increasing resolution, but eventually reaches an asymptotic limit at high Reynolds numbers. Although most supernova simulation may not fully reach this asymptotic regime, they do not fall far short of it: The works of Handy et al. (Reference Handy, Plewa and Odrzywołek2014) and Radice et al. (Reference Radice, Couch and Ott2015, Reference Radice, Ott, Abdikamalov, Couch, Haas and Schnetter2016) suggest that this level of accuracy in the turbulent dissipation can be reached even with moderate resolution (< 100 grid points per direction, ~ 2° resolution in angle in spherical polar coordinates) in the gain region with higher order reconstruction methods and accurate Riemann solvers. Problems due to stringent resolution requirements may still lurk elsewhere, though, e.g., concerning SASI growth rates as already pointed out 10 yr ago by Sato, Foglizzo, & Fromang (Reference Sato, Foglizzo and Fromang2009). Resolution studies and cross-comparisons thus remain useful, though cross-comparisons are of course hampered by the different physical assumptions used in different codes and the feedback processes in the supernova core. For this reason, a direct comparison of, e.g., turbulent kinetic energies and Mach numbers between different models is not necessarily meaningful. The dimensionless coefficients governing the dynamics of non-radial instabilities such the proportionality constant
![]() $\eta _{\rm conv}=v_{\rm turb}/[\dot{q_\nu } (r_{\rm sh}-r_{\rm g})]$
in Equation (18) or the quality factor
$\eta _{\rm conv}=v_{\rm turb}/[\dot{q_\nu } (r_{\rm sh}-r_{\rm g})]$
in Equation (18) or the quality factor
![]() $\mathcal {Q}$
in Equation (17) may be more useful metrics of comparison.
$\mathcal {Q}$
in Equation (17) may be more useful metrics of comparison.
4.2 Neutrino transport
The requirements on the treatment of neutrino heating and cooling are highly problem-dependent. The physical principles behind convection and the SASI can be studied with simple heating and cooling functions in a light-bulb approach, and such an approach is indeed often advantageous as it removes some of the feedback processes that complicate the analysis of full-scale supernova simulations. To model the fate and explosion properties of concrete progenitors in a predictive manner, some form of neutrino transport is required, and depending on the targeted level of accuracy, the requirements become more stringent; e.g., higher standards apply when it comes to predicting supernova nucleosynthesis. There is no perfect method for neutrino transport in supernovae as yet. Efforts towards a solution of the full 6D Boltzmann equation are underway (e.g., Cardall, Endeve, & Mezzacappa Reference Cardall, Endeve and Mezzacappa2013; Peres et al. Reference Peres, Penner, Novak and Bonazzola2014; Radice et al. Reference Radice, Abdikamalov, Rezzolla and Ott2013; Nagakura, Sumiyoshi, & Yamada Reference Nagakura, Sumiyoshi and Yamada2014), but not yet ripe for real supernova simulations.
Neutrino transport algorithms (beyond fully parameterised light-bulb models) currently in use for 1D and multi-D models include:
-
• leakage schemes as, e.g., in O’Connor & Ott (Reference O’Connor and Ott2010, Reference O’Connor and Ott2011), Ott et al. (Reference Ott2013), and Couch & O’Connor (Reference Couch and O’Connor2014);
-
• the isotropic diffusion source approximation (IDSA) of Liebendörfer, Whitehouse, & Fischer (Reference Liebendörfer, Whitehouse and Fischer2009);
-
• one-moment closure schemes employing prescribed flux factors (Scheck et al. Reference Scheck, Kifonidis, Janka and Müller2006), flux-limited diffusion as in the Vulcan code (Livne et al. Reference Livne, Burrows, Walder and Lichtenstadt2004; Walder et al. Reference Walder, Burrows, Ott, Livne, Lichtenstadt and Jarrah2005), the Chimera code (Bruenn Reference Bruenn1985; Bruenn et al. Reference Bruenn2013), and the Castro code (Zhang et al. Reference Zhang, Howell, Almgren, Burrows, Dolence and Bell2013; Dolence, Burrows, & Zhang Reference Dolence, Burrows and Zhang2015), or a dynamic closure as in the coconut-fmt code;
-
• two-moment methods employing algebraic closures in 1D (O’Connor Reference O’Connor2015) and multi-D (Obergaulinger & Janka Reference Obergaulinger and Janka2011; Kuroda et al. Reference Kuroda, Kotake and Takiwaki2012; Just et al. Reference Just, Obergaulinger and Janka2015; Skinner et al. Reference Skinner, Burrows and Dolence2016; O’Connor & Couch Reference O’Connor and Couch2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016; Kuroda, Takiwaki, & Kotake Reference Kuroda, Takiwaki and Kotake2016) or variable Eddington factors from a model Boltzmann equation (Burrows et al. Reference Burrows, Young, Pinto, Eastman and Thompson2000b; Rampp & Janka Reference Rampp and Janka2002; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a; Müller et al. Reference Müller, Janka and Dimmelmeier2010);
-
• discrete ordinate methods for the Boltzmann equation, mostly in 1D (Mezzacappa & Bruenn Reference Mezzacappa and Bruenn1993; Yamada, Janka, & Suzuki Reference Yamada, Janka and Suzuki1999; Liebendörfer et al. Reference Liebendörfer, Messer, Mezzacappa, Bruenn, Cardall and Thielemann2004) or, at the expense of other simplifications, in multi-D (Livne et al. Reference Livne, Burrows, Walder and Lichtenstadt2004; Ott et al. Reference Ott, Burrows, Dessart and Livne2008; Nagakura et al. Reference Nagakura, Iwakami, Furusawa, Sumiyoshi, Yamada, Matsufuru and Imakura2016; only for static configurations: Sumiyoshi et al. Reference Sumiyoshi, Takiwaki, Matsufuru and Yamada2015).
This list should not be taken as a hierarchy of accuracy; it mere reflects crudely the rigour in treating one aspect of the neutrino transport problem, i.e., the angle-dependence of the radiation field in phase space. When assessing neutrino transport methodologies, there are other, equally important factors that need to be taken into account when comparing different modelling approaches.
Most importantly, the sophistication of the microphysics varies drastically. On the level of one-moment and two-moment closure models, it is rather the neutrino microphysics that decides about the quantitative accuracy. The 3D models of the MPA-QUB group (Melson et al. Reference Melson, Janka and Marek2015a, Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b; Janka et al. Reference Janka, Melson and Summa2016) and the Chimera team (Lentz et al. Reference Lentz2015) currently represent the state-of-the-art in this respect; though other codes (O’Connor Reference O’Connor2015; Just et al. Reference Just, Obergaulinger and Janka2015; Skinner et al. Reference Skinner, Burrows and Dolence2016; Kuroda et al. Reference Kuroda, Takiwaki and Kotake2016) come close.
Often, the neutrino physics is simplified considerably, however. Some simulations disregard heavy flavour neutrinos altogether (e.g., Suwa et al. Reference Suwa, Kotake, Takiwaki, Whitehouse, Liebendörfer and Sato2010; Takiwaki et al. Reference Takiwaki, Kotake and Suwa2012), or only treat them by means of a leakage scheme (Takiwaki et al. Reference Takiwaki, Kotake and Suwa2014; Pan et al. Reference Pan, Liebendörfer, Hempel and Thielemann2016). This affects the contraction of the proto-neutron star and thus indirectly alters the emission of electron flavour neutrinos and the effective inner boundary for the gain region as well.
Amongst multi-D codes, energy transfer due to inelastic neutrino-electron scattering (NES) is routinely taken into account only in the Vertex code (Rampp & Janka Reference Rampp and Janka2002; Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a; Müller et al. Reference Müller, Janka and Dimmelmeier2010) of the MPA-QUB collaboration, the Alcar code (Just et al. Reference Just, Obergaulinger and Janka2015), the Chimera code of the Chimera team (Bruenn Reference Bruenn1985; Bruenn et al. Reference Bruenn2013), and the Fornax code of the Princeton group (Skinner et al. Reference Skinner, Burrows and Dolence2016). Without NES (Bruenn Reference Bruenn1985) and modern electron capture rates (Langanke et al. Reference Langanke2003), the core mass at bounce is larger and the shock propagates faster at early times (Lentz et al. Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012a, Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012b). In multi-D, this can lead to unduly strong prompt convection. Because of this problem, a closer look at the bounce dynamics is in order whenever explosions occur suspiciously early (< 100 ms after bounce). Parameterising deleptonisation during collapse (Liebendörfer Reference Liebendörfer2005) provides a workaround to some extent.
The recoil energy transfer in neutrino-nucleon scattering effectively reshuffles heavy flavour neutrino luminosity to electron flavour luminosity in the cooling region (Müller et al. Reference Müller, Janka and Marek2012a) and hence critically influences the heating conditions in the gain region. Amongst multi-D codes, only Vertex and Chimera currently take this into account, and the code coconut-fmt (Müller & Janka Reference Müller and Janka2015) uses an effective absorption opacity for heavy flavour neutrinos to mimic this phenomenon.
Vertex and Chimera are also the only multi-D codes to include the effect of nucleon–nucleon correlations (Burrows & Sawyer Reference Burrows and Sawyer1998, Reference Burrows and Sawyer1999; Reddy et al. Reference Reddy, Prakash, Lattimer and Pons1999) on absorption and scattering opacities. Nucleon correlations have a huge impact during the cooling phase, which they shorten by a factor of several (Hüdepohl et al. Reference Hüdepohl, Müller, Janka, Marek and Raffelt2009). Their role during the first second after bounce is not well explored. Considering that the explosion energetics are determined on a timescale of seconds (Müller Reference Müller2015; Bruenn et al. Reference Bruenn2016), it is plausible that the increased diffusion luminosity from the neutron star due to in-medium corrections to the opacities may influence the explosion energy to some extent.
Gray schemes (Fryer & Warren Reference Fryer and Warren2002; Scheck et al. Reference Scheck, Kifonidis, Janka and Müller2006; Kuroda et al. Reference Kuroda, Kotake and Takiwaki2012) cannot model neutrino heating and cooling accurately; an energy-dependent treatment is needed because of the emerging neutrino spectra are highly non-thermal with a pinched high-energy tail (Janka & Hillebrandt Reference Janka and Hillebrandt1989; Keil, Raffelt, & Janka Reference Keil, Raffelt and Janka2003).
Some multi-D codes use the ray-by-ray-plus approximation (Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a), which exaggerates angular variations in the radiation field, and has been claimed to lead to spuriously early explosions in some cases in conjunction with artificially strong sloshing motions in 2D (Skinner et al. Reference Skinner, Burrows and Dolence2016). Whether this is a serious problem is unclear in the light of similar results of Summa et al. (Reference Summa, Hanke, Janka, Melson, Marek and Müller2016) for ray-by-ray-plus models and O’Connor & Couch (Reference O’Connor and Couch2015) for fully two-dimensional two-moment transport. On the other hand, fully multi-dimensional flux limited diffusion approaches smear out angular variations in the radiation field too strongly (Ott et al. Reference Ott, Burrows, Dessart and Livne2008).
Neglecting all or part of the velocity-dependent terms in the transport equations potentially has serious repercussions. Neglecting only observer correction (Doppler shift, compression work, etc.) as, e.g., in Livne et al. (Reference Livne, Burrows, Walder and Lichtenstadt2004) can already have an appreciable impact on the dynamics (Buras et al. Reference Buras, Rampp, Janka and Kifonidis2006a; Lentz et al. Reference Lentz, Mezzacappa, Bronson Messer, Hix and Bruenn2012a). Disregarding even the co-advection of neutrinos with the fluid (O’Connor Reference O’Connor2015; Roberts et al. Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016) formally violates the diffusion limit and effectively results in an extra source term in the optically thick regime due to the equilibration of matter with lagging neutrinos:
where E eq is the equilibrium neutrino energy density. Judging from the results of O’Connor & Couch (Reference O’Connor and Couch2015) and Roberts et al. (Reference Roberts, Ott, Haas, O’Connor, Diener and Schnetter2016), which are well in line with results obtained with other codes, the effect may not be too serious in practice, though. It should also be noted that (semi-)stationary approximations of the transport equation (Liebendörfer et al. Reference Liebendörfer, Whitehouse and Fischer2009; Müller & Janka Reference Müller and Janka2015) avoid this problem even if advection terms are not explicitly included.
Leakage-based schemes as used, e.g., in Ott et al. (Reference Ott2012), Couch & Ott (Reference Couch and Ott2015), Abdikamalov et al. (Reference Abdikamalov2015), and Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) also manifestly fail to reproduce the diffusion limit. Here, however, the violation of the diffusion limit is unmistakable and can severely affect the stratification of the gain region and, in particular, the cooling region. Together with ad hoc choices for the flux factor for calculating the heating rate, this can result in inordinately high heating efficiencies immediately after bounce and a completely inverted hierarchy of neutrino mean energies. It compromises the dynamics of leakage models to an extent that they can only be used for very qualitative studies of the multi-D flow in the supernova core.
There is in fact no easy lesson to be learned from the pitfalls and complications that we have outlined. In many contexts, approximations for the neutrino transport are perfectly justified for a well-circumscribed problem, and feedback processes sometimes mitigate the effects of simplifying assumptions. It is crucial, though, to be aware of the impact that such approximations can potentially have, and our (incomplete) enumeration is meant to provide some guidance in this respect.
5 FUTURE DIRECTIONS: MULTI-D EFFECTS IN SUPERNOVA PROGENITORS
Given the sophisticated simulation methodology employed in the best currently available supernova codes, one may be tempted to ask whether another missing ingredient for robust neutrino-driven explosion is to be sought elsewhere. One recent idea, first proposed by Couch & Ott (Reference Couch and Ott2013), focusses on the progenitor models used in supernova simulations. The twist consists in an extra ‘forcing’ of the non-radial motions in the gain region by large seed perturbations in the infalling shells. Such seed perturbations will arise naturally in active convective burning shells (O burning, and perhaps also Si burning) that reach the shock during the first few hundred milliseconds after bounce.
5.1 Role of pre-collapse perturbations in the neutrino-driven mechanism
In default of multi-D progenitor models, this new variation of the neutrino-driven mechanism was initially studied by imposing large initial perturbations by hand in leakage-based simulations (Couch & Ott Reference Couch and Ott2013, Reference Couch and Ott2015) and multi-group neutrino hydrodynamics simulations (Müller & Janka Reference Müller and Janka2015); the earlier light-bulb-based models of Fernández (Reference Fernández2012) also touched parts of the problem. The results of these investigations were mixed, even though some of these calculations employed perturbations far in excess of what estimates based on mixing-length theory (Biermann Reference Biermann1932; Böhm-Vitense Reference Böhm-Vitense1958) suggest: For example, Couch & Ott (Reference Couch and Ott2013) used transverse velocity perturbations with a peak Mach number of Ma = 0.2 in their 3D models, and found a small beneficial effect on shock revival, which, however, was tantamount to a change of the critical neutrino luminosity by only
![]() $\mathord {\sim } 2\%$
. The more extensive 2D parameter study of different solenoidal and compressive velocity perturbations and density perturbations by Müller & Janka (Reference Müller and Janka2015) established that both significant perturbation velocities (Ma ≳ 0.1) as well as large-scale angular structures (angular wavenumber ℓ ≲ 4) need to be present in active convective shell in order to reduce the critical luminosity appreciably, i.e., by ≳ 10%.
$\mathord {\sim } 2\%$
. The more extensive 2D parameter study of different solenoidal and compressive velocity perturbations and density perturbations by Müller & Janka (Reference Müller and Janka2015) established that both significant perturbation velocities (Ma ≳ 0.1) as well as large-scale angular structures (angular wavenumber ℓ ≲ 4) need to be present in active convective shell in order to reduce the critical luminosity appreciably, i.e., by ≳ 10%.
These parametric studies already elucidated the physical mechanism whereby pre-collapse perturbations can facilitate shock revival. Müller & Janka (Reference Müller and Janka2015) highlighted the importance both of the infall phase as well as the interaction of the perturbations with the shock. Linear perturbation theory shows that the initial perturbations are amplified during collapse (Lai & Goldreich Reference Lai and Goldreich2000; Takahashi & Yamada Reference Takahashi and Yamada2014). This not only involves a strong growth of transverse velocity perturbations as δvt ∝r −1, but even more importantly a conversion of the initially dominating solenoidal velocity perturbations with Mach number Maconv into density perturbations δρ/ρ ≈ Ma (Müller & Janka Reference Müller and Janka2015) during collapse, i.e., the relative density perturbations are much larger ahead of the shock than during quasi-stationary convection, where δρ/ρ ≈ Ma2.Footnote 11
Large density perturbations ahead of the shock imply a pronounced asymmetry in the pre-shock ram pressure and deform the shock, creating fast lateral flows as well as post-shock density and entropy perturbations that buoyancy then converts into turbulent kinetic energy. The direct injection of kinetic energy due to infalling turbulent motions may also play a role (Abdikamalov et al. Reference Abdikamalov, Zhaksylykov, Radice and Berdibek2016), though it appears to be subdominant (Müller & Janka Reference Müller and Janka2015; Müller et al. Reference Müller, Viallet, Heger and Janka2016a). A very crude estimate for the generation of additional turbulent kinetic energy due to the different processes as well as turbulent damping in the post-shock region has been used by Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) to estimate the reduction of the critical luminosity as
in terms of the pre-collapse Mach number Maconv of eddies from shell burning, their typical angular wavenumber ℓ, and the accretion efficiency
![]() $\eta _{\rm acc}=L_\nu /(GM \dot{M} r_{\rm gain})$
and heating efficiency ηheat during the pre-explosion phase.
$\eta _{\rm acc}=L_\nu /(GM \dot{M} r_{\rm gain})$
and heating efficiency ηheat during the pre-explosion phase.
A more rigorous understanding of the interaction between infalling perturbations, the shock, and non-radial motions in the post-shock region is currently emerging: Abdikamalov et al. (Reference Abdikamalov, Zhaksylykov, Radice and Berdibek2016) studied the effect of upstream perturbations on the shock using the linear interaction approximation of Ribner (Reference Ribner1953) and argue, in line with Müller et al. (Reference Müller, Viallet, Heger and Janka2016a), that a reduction of the critical luminosity by > 10% is plausible. Their estimate may, however, be even too pessimistic as they neglect acoustic perturbations upstream of the shock. Different from Abdikamalov et al. (Reference Abdikamalov, Zhaksylykov, Radice and Berdibek2016), the recent analysis of Takahashi et al. (Reference Takahashi, Iwakami, Yamamoto and Yamada2016) also takes into account that instabilities or stabilisation mechanisms operate in the post-shock flow, and studied the (linear) response of convective and SASI eigenmodes to forcing by infalling perturbations. A rigorous treatment along these lines that explains the saturation of convective and SASI modes as forced oscillators with non-linear damping remains desirable.
5.2 The advent of 3D supernova progenitor models
The parametric studies of Couch & Ott (Reference Couch and Ott2013, Reference Couch and Ott2015) and Müller & Janka (Reference Müller and Janka2015) still hinged on uncertain assumptions about the magnitude and scale of the seed perturbations left by O and Si shell burning. Various pioneering studies of advanced shell burning stages (O, Si, C burning) (Arnett Reference Arnett1994; Bazan & Arnett Reference Bazan and Arnett1994, Reference Bazan and Arnett1998; Asida & Arnett Reference Asida and Arnett2000; Kuhlen, Woosley, & Glatzmaier Reference Kuhlen, Woosley, Glatzmaier, Turcotte, Keller and Cavallo2003; Meakin & Arnett Reference Meakin and Arnett2006, Reference Meakin and Arnett2007b, Reference Meakin and Arnett2007a; Arnett & Meakin Reference Arnett and Meakin2011; Viallet et al. Reference Viallet, Meakin, Arnett and Mocák2013; Chatzopoulos, Graziani, & Couch Reference Chatzopoulos, Graziani and Couch2014) merely indicated that convective Mach numbers of a few 10−2 and the formation of large-scale eddies are plausible, but did not permit a clear-cut judgement about whether pre-collapse perturbations play a dynamical role in the neutrino-driven mechanism.
The situation has changed recently with the advent of models of convective shell burning that have been evolved up to collapse. The idea here is to calculate the last few minutes prior to collapse to obtain multi-dimensional initial conditions, whilst ignoring potential long-term effects in 3D such as convective boundary mixing (which we discuss in Section 5.3). Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) performed a 3D simulation of the last minutes of Si shell burning in a
![]() $15\,\text{M}_\odot$
star. The simulation was limited to an octant, and nuclear quasi-equilibrium during Si burning was only treated with a small network. More importantly, the evolution towards collapse was artificially accelerated by artificially increasing electron capture rates in the iron core. As pointed out by Müller et al. (Reference Müller, Viallet, Heger and Janka2016a), this can alter the shell evolution and the convective velocities considerably. Since the shell configuration and structure at collapse varies considerably in 1D models, such an exploratory approach is nonetheless still justified (see below).
$15\,\text{M}_\odot$
star. The simulation was limited to an octant, and nuclear quasi-equilibrium during Si burning was only treated with a small network. More importantly, the evolution towards collapse was artificially accelerated by artificially increasing electron capture rates in the iron core. As pointed out by Müller et al. (Reference Müller, Viallet, Heger and Janka2016a), this can alter the shell evolution and the convective velocities considerably. Since the shell configuration and structure at collapse varies considerably in 1D models, such an exploratory approach is nonetheless still justified (see below).
Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) explored the more generic case where Si shell burning is extinguished before collapse and the O shell is the innermost active convective region. In their 3D simulation of the last 5 min of O shell burning in an
![]() $18\,\text{M}_\odot$
progenitor, they circumvented the aforementioned problems by excising the non-convective Fe and Si core and contracting it in accordance with a 1D stellar evolution model. Moreover, Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) simulated the entire sphere using an overset Yin–Yang grid (Kageyama & Sato Reference Kageyama and Sato2004; Wongwathanarat, Hammer, & Müller Reference Wongwathanarat, Hammer and Müller2010) as implemented (with some improvements) in the Prometheus supernova code (Melson Reference Melson2013; Melson et al. Reference Melson, Janka and Marek2015a).
$18\,\text{M}_\odot$
progenitor, they circumvented the aforementioned problems by excising the non-convective Fe and Si core and contracting it in accordance with a 1D stellar evolution model. Moreover, Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) simulated the entire sphere using an overset Yin–Yang grid (Kageyama & Sato Reference Kageyama and Sato2004; Wongwathanarat, Hammer, & Müller Reference Wongwathanarat, Hammer and Müller2010) as implemented (with some improvements) in the Prometheus supernova code (Melson Reference Melson2013; Melson et al. Reference Melson, Janka and Marek2015a).
The implications of these simulations for supernova modelling are mixed. The typical convective Mach number in Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) was only
![]() $\mathord {\sim }0.02$
, and whilst they found large-scale motions, the scale of the pre-collapse perturbations was still limited by the restriction to octant symmetry. Perturbations of such a magnitude are unlikely to reduce the critical luminosity considerably (Section 5.1). Consequently, supernova simulations starting from 1D and 3D initial conditions using a leakage scheme performed by Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) did not show a qualitative difference; both 1D and 3D initial conditions result in explosions, though the shock expands slightly faster in the latter case. The use of a leakage scheme and possible effects of stochasticity preclude definite conclusions from these first results.
$\mathord {\sim }0.02$
, and whilst they found large-scale motions, the scale of the pre-collapse perturbations was still limited by the restriction to octant symmetry. Perturbations of such a magnitude are unlikely to reduce the critical luminosity considerably (Section 5.1). Consequently, supernova simulations starting from 1D and 3D initial conditions using a leakage scheme performed by Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) did not show a qualitative difference; both 1D and 3D initial conditions result in explosions, though the shock expands slightly faster in the latter case. The use of a leakage scheme and possible effects of stochasticity preclude definite conclusions from these first results.
The typical convective Mach number in the
![]() $18\,\text{M}_\odot$
model of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) is considerably larger (
$18\,\text{M}_\odot$
model of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) is considerably larger (
![]() $\mathord {\sim }0.1$
), and their simulation also showed the emergence of a bipolar (ℓ = 2) flow structure, which lead them to predict a relatively large reduction of the critical luminosity by 12. . .24%, which would accord a decisive role to 3D initial conditions in the neutrino-driven mechanism at least in some progenitors. A first 3D multi-group neutrino hydrodynamics simulation of their
$\mathord {\sim }0.1$
), and their simulation also showed the emergence of a bipolar (ℓ = 2) flow structure, which lead them to predict a relatively large reduction of the critical luminosity by 12. . .24%, which would accord a decisive role to 3D initial conditions in the neutrino-driven mechanism at least in some progenitors. A first 3D multi-group neutrino hydrodynamics simulation of their
![]() $18\,\text{M}_\odot$
progenitor using the coconut-fmt code appears to bear this out (Müller et al. in preparation): Figure 5 shows the shock radius both for two simulations using 3D and 1D initial conditions, respectively: In the former case, shock revival occurs around 250 ms after bounce thanks to the infall of the convectively perturbed oxygen shell, whereas no explosion develops in the reference simulation by the end of the run more than 600 ms after bounce. An analysis of the heating conditions indicates that the non-exploding reference model is clearly not a near miss at 250 ms. The effect of 3D initial conditions is thus unambiguously large and sufficient to change the evolution qualitatively. Moreover, the model indicates that realistic supernova explosion energies are within reach in 3D as well: The diagnostic explosion energy reaches 5 × 1050 erg and still continues to mount by the end of the simulation 1.43 s after bounce. It is also interesting to note that the initial asymmetries are clearly reflected in the explosion geometry (Figure 6) as speculated by Arnett & Meakin (Reference Arnett and Meakin2011). Incidentally, the model also shows that the accretion of convective regions does not lead to the formation of the ‘accretion belts’ proposed by Gilkis & Soker (Reference Gilkis and Soker2014) as an ingredient for their jittering-jet mechanism.
$18\,\text{M}_\odot$
progenitor using the coconut-fmt code appears to bear this out (Müller et al. in preparation): Figure 5 shows the shock radius both for two simulations using 3D and 1D initial conditions, respectively: In the former case, shock revival occurs around 250 ms after bounce thanks to the infall of the convectively perturbed oxygen shell, whereas no explosion develops in the reference simulation by the end of the run more than 600 ms after bounce. An analysis of the heating conditions indicates that the non-exploding reference model is clearly not a near miss at 250 ms. The effect of 3D initial conditions is thus unambiguously large and sufficient to change the evolution qualitatively. Moreover, the model indicates that realistic supernova explosion energies are within reach in 3D as well: The diagnostic explosion energy reaches 5 × 1050 erg and still continues to mount by the end of the simulation 1.43 s after bounce. It is also interesting to note that the initial asymmetries are clearly reflected in the explosion geometry (Figure 6) as speculated by Arnett & Meakin (Reference Arnett and Meakin2011). Incidentally, the model also shows that the accretion of convective regions does not lead to the formation of the ‘accretion belts’ proposed by Gilkis & Soker (Reference Gilkis and Soker2014) as an ingredient for their jittering-jet mechanism.

Figure 5. Impact of pre-collapse asphericities on shock revival in 3D multi-group neutrino hydrodynamics simulations of an
![]() $18\,\text{M}_\odot$
progenitor. The plot shows the minimum, maximum (solid lines), and average (dashed) shock radii for a model using 3D initial conditions (black) from the O shell burning simulation of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) and a spherically averaged version of the same progenitor (red). The gain radius (dash-dotted) and the proto-neutron star radius (dotted, defined by a fiducial density of 1011 g cm−3) are shown only for the model starting from 3D initial conditions; they are virtually identical for both models. A neutrino-driven explosion is triggered roughly 0.25 s after bounce aided by the infall of the convectively perturbed oxygen shell in the model using 3D initial conditions. The simulation starting from the 1D progenitor model exhibits steady and strong SASI oscillations after 0.25 s, but does not explode at least for another 0.3 s.
$18\,\text{M}_\odot$
progenitor. The plot shows the minimum, maximum (solid lines), and average (dashed) shock radii for a model using 3D initial conditions (black) from the O shell burning simulation of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) and a spherically averaged version of the same progenitor (red). The gain radius (dash-dotted) and the proto-neutron star radius (dotted, defined by a fiducial density of 1011 g cm−3) are shown only for the model starting from 3D initial conditions; they are virtually identical for both models. A neutrino-driven explosion is triggered roughly 0.25 s after bounce aided by the infall of the convectively perturbed oxygen shell in the model using 3D initial conditions. The simulation starting from the 1D progenitor model exhibits steady and strong SASI oscillations after 0.25 s, but does not explode at least for another 0.3 s.

Figure 6. Top row: Radial velocity in units of cm s−1 (top left) and mass fraction of Si (top right) at the onset of collapse in the 3D progenitor model of an
![]() $18\,\text{M}_\odot$
star of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a). Bottom row: Entropy in units of kb
/nucleon (bottom left) and mass fraction of Si (bottom right) in the ensuing neutrino-driven explosion 1.43 s after bounce from. All plots show equatorial slices from the 3D simulation. It can be seen that the geometry of the initial conditions is still imprinted on the explosion to some extent with stronger shock expansion in the direction of updrafts of Si rich ashes in the O burning shell. This is a consequence of the forced deformation of the shock around the onset of the explosion.
$18\,\text{M}_\odot$
star of Müller et al. (Reference Müller, Viallet, Heger and Janka2016a). Bottom row: Entropy in units of kb
/nucleon (bottom left) and mass fraction of Si (bottom right) in the ensuing neutrino-driven explosion 1.43 s after bounce from. All plots show equatorial slices from the 3D simulation. It can be seen that the geometry of the initial conditions is still imprinted on the explosion to some extent with stronger shock expansion in the direction of updrafts of Si rich ashes in the O burning shell. This is a consequence of the forced deformation of the shock around the onset of the explosion.
Whether 3D initial conditions generally play an important role in the neutrino-driven mechanism cannot be answered by studying just two progenitors, aside from the fact that the models of Couch et al. (Reference Couch, Chatzopoulos, Arnett and Timmes2015) and Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) still suffer from limitations. The properties (width, nuclear energy generation rate) and the configuration of convective burning shells at collapse varies tremendously across different progenitors in 1D stellar evolution models as, e.g., the Kippenhahn diagrams in the literature indicate (Heger, Langer, & Woosley Reference Heger, Langer and Woosley2000; Chieffi & Limongi Reference Chieffi and Limongi2013; Sukhbold & Woosley Reference Sukhbold and Woosley2014; Cristini et al. Reference Cristini, Meakin, Hirschi, Arnett, Georgy and Viallet2016). The interplay of convective burning, neutrino cooling, and the contraction/re-expansion of the core and the shells sometimes leave inversions in the temperature stratification and a complicating layering of material at different nuclear processing stages. For this reason, 1D stellar evolution models sometimes show a highly dynamic behaviour immediately prior to collapse with shells of incompletely burnt material flaring up below the innermost active shell. This is illustrated by follow-up work to Müller et al. (Reference Müller, Viallet, Heger and Janka2016a) shown in Figure 7, where a partially processed layer with unburnt O becomes convective shortly before collapse due to violent burning and is about to merge with the overlying O/Ne shell before collapse intervenes.

Figure 7. Radial velocity in units of cm s−1 (shown in 90°-wedges in the left half of each plot) and mass fraction X
O of oxygen during the last minutes of shell burning in an
![]() $12.5\,\text{M}_\odot$
progenitor. Snapshots at 175 s (top left), 66 s (top right), 24 s (bottom left) before collapse, and at the onset of collapse (bottom right) are shown. The residual oxygen in a thin, almost O-depleted shell (red) starts to burn vigorously due to the contraction of the core (top right). As the entropy of this shell increases and matches that of an almost unprocessed, O-rich shell (blue) and the active Ne shell (cyan), it expands outwards by ‘encroachment’ (bottom left), but there is insufficient time for the shells to merge completely before collapse (bottom right). Note that this is not a qualitatively new phenomenon in 3D; similar events occur in 1D stellar evolution models.
$12.5\,\text{M}_\odot$
progenitor. Snapshots at 175 s (top left), 66 s (top right), 24 s (bottom left) before collapse, and at the onset of collapse (bottom right) are shown. The residual oxygen in a thin, almost O-depleted shell (red) starts to burn vigorously due to the contraction of the core (top right). As the entropy of this shell increases and matches that of an almost unprocessed, O-rich shell (blue) and the active Ne shell (cyan), it expands outwards by ‘encroachment’ (bottom left), but there is insufficient time for the shells to merge completely before collapse (bottom right). Note that this is not a qualitatively new phenomenon in 3D; similar events occur in 1D stellar evolution models.
The diverse shell configurations in supernova progenitors need to be thoroughly explored in 3D before a general verdict on the efficacy of convective seed perturbations in aiding shock revival can be given. Since the bulk properties of the flow (typical velocity, eddy scales) in the interior of the convective shells are apparently well captured by mixing-length theory (Arnett, Meakin, & Young Reference Arnett, Meakin and Young2009; Müller et al. Reference Müller, Viallet, Heger and Janka2016a), the convective Mach numbers and eddy scales predicted from 1D stellar evolution models can provide guidance for exploring interesting spots in parameter space.
5.3 Convective boundary mixing—how uncertain is the structure of supernova progenitors?
In what we discussed so far, we have considered multi-D effects in advanced convective burning stages merely because of their role in determining the initial conditions for stellar collapse. They could also have an important effect on the secular evolution of massive stars long before the supernova explosion, and thereby change critical structural properties of the progenitors, such as the compactness parameter (O’Connor & Ott Reference O’Connor and Ott2011). Whilst mixing-length theory (Biermann Reference Biermann1932; Böhm-Vitense Reference Böhm-Vitense1958) may adequately describe the mixing in the interior of convective zones,Footnote 12 the mixing across convective boundaries is less well understood, and may play an important role in determining the pre-collapse structure of massive stars along with other non-convective processes (e.g., Heger et al. Reference Heger, Langer and Woosley2000; Maeder & Meynet Reference Maeder and Meynet2004; Heger et al. Reference Heger, Woosley and Spruit2005; Young et al. Reference Young, Meakin, Arnett and Fryer2005; Talon & Charbonnel Reference Talon and Charbonnel2005; Cantiello et al. Reference Cantiello, Mankovich, Bildsten, Christensen-Dalsgaard and Paxton2014) for mixing and angular momentum transport. That some mixing beyond the formally unstable regions needs to be included has long been known (Kippenhahn & Weigert Reference Kippenhahn and Weigert1990). Phenomenological recipes for this include extending the mixed region by a fraction of the local pressure scale height, or adding diffusive mixing in the formally stable regions with a calibrated functional dependence on the distance to the boundary (Freytag, Ludwig, & Steffen Reference Freytag, Ludwig and Steffen1996; Herwig et al. Reference Herwig, Bloecker, Schoenberner and El Eid1997).
The dominant mechanism for convective boundary mixing during advanced burning stages is entrainment (Fernando Reference Fernando1991; Meakin & Arnett Reference Meakin and Arnett2007b; Viallet et al. Reference Viallet, Meakin, Prat and Arnett2015) due to the growth of the Kelvin–Helmholtz or Holmböe instability at the shell interfaces. For interfaces with a discontinuous density jump as often encountered in the interiors of evolved massive stars, the relevant dimensionless number for such shear-driven instabilities is the bulk Richardson number RiB. For entrainment driven by turbulent convection, one has
in terms of the local gravitational acceleration g, the density contrast δρ/ρ at the interface, the typical convective velocity v conv in the convective region, and the integral scale l of the convective eddies. Equating l with the pressure scale height l = P/ρg allows us to re-express RiB in terms of the convective Mach number Maconv and the adiabatic exponent γ:
Deep in the stellar core, Maconv is typically small during most evolutionary phases, and RiB is large so that the convective boundaries are usually very ‘stiff’ (Cristini et al. Reference Cristini, Meakin, Hirschi, Arnett, Georgy and Viallet2016).
Various power laws for the entrainment rate have been proposed in the general fluid dynamics literature (Fernando Reference Fernando1991; Strang & Fernando Reference Strang and Fernando2001) and astrophysical studies (Meakin & Arnett Reference Meakin and Arnett2007b) of interfacial mixing driven by turbulent convection on one side of the interface. In the astrophysical context, it is convenient to translate these into a power law for the mass flux
![]() $\dot{M}_{\rm entr}$
of entrained material into the convective region,
$\dot{M}_{\rm entr}$
of entrained material into the convective region,
with a proportionality constant A and a power-law exponent n. Here, ρ is the density on the convective side of the interface.
A number of laboratory studies (Fernando Reference Fernando1991; Strang & Fernando Reference Strang and Fernando2001) and astrophysical simulations (Meakin & Arnett Reference Meakin and Arnett2007b; Müller et al. Reference Müller, Viallet, Heger and Janka2016a) suggest values of A ~ 0.1 and n = 1. This can be understood heuristically by assuming that layer of width δl ~ Av
2
conv/(g δρ/ρ) always remains well mixed,Footnote
13
and that a fraction δl/l of the mass flux
![]() $\dot{M}_{\rm down} =2 \pi r^2 \rho v_{\rm conv}$
in the convective downdrafts comes from this mixed layer.
$\dot{M}_{\rm down} =2 \pi r^2 \rho v_{\rm conv}$
in the convective downdrafts comes from this mixed layer.
This estimate is essentially equivalent to another one proposed in a slightly different context (ingestion of unburnt He during core-He burning; Constantino et al. Reference Constantino, Campbell, Christensen-Dalsgaard and Stello2015) by Spruit (Reference Spruit2015), who related the ingestion (or entrainment) rate into a convective zone to the convective luminosity L conv. Spruit’s argument can be interpreted as one based on energy conservation; work is needed to pull material with positive buoyancy from an outer shell down into a deeper one, and the energy that is tapped for this purpose comes from convective motions. Since L conv ~ 4πr 2ρv 3 conv, we can write Equation (35) as
which directly relates the entrainment rate to the ratio of L conv and the potential energy of material with positive buoyancy after downward mixing over an eddy scale l. The entrainment law (35), the argument of Spruit (Reference Spruit2015), and the proportionality of the entrainment rate with L conv found in the recent work of Jones et al. (Reference Jones, Andrassy, Sandalski, Davis, Woodward and Herwig2016b) on entrainment in highly resolved idealised 3D simulation of O shell burning appear to be different sides of the same coin.
5.4 Long-term effects of entrainment on the shell structure?
How much will entrainment affect the shell structure of massive stars in the long term? First numerical experiments based on the entrainment law of Meakin & Arnett (Reference Meakin and Arnett2007b) were performed by Staritsin (Reference Staritsin2013) for massive stars on the main sequenceFootnote 14 and did not reveal dramatic differences in the size of the convective cores compared to more familiar, calibrated recipes for core overshooting.
Taking Equation (36) at face value allows some interesting speculations about the situation during advanced burning stages. Since the convective motions ultimately feed on the energy generated by nuclear burning E burn, we can formulate a time-integrated version of Equation (36) for the entrained mass ΔM entr over the life time of a convective shell:
where M shell is the (final) mass of the shell, and ΔQ is the nuclear energy release per unit mass. With GM/r ~ 2e int in stellar interiors, we can estimate ΔM entr in terms ΔQ and the internal energy e int at which the burning occurs,Footnote 15
For O burning at ~ 2 × 109 K and with ΔQ ≈ 0.5 MeV/nucleon, the factor ΔQ/(2e int) is of order unity. Typically, the density contrast δρ/ρ between adjacent shells is also not too far below unity. Since A ≈ 0.1, this suggests that the shell growth due to entrainment comes up to at most a few tens of percent during O shell burning unless δρ/ρ is rather small to begin with. Thus, a result of entrainment might be that convective zones may swallow thin, unburnt shells with a small density contrast before bounce, whereas the large entropy jumps between the major shells are maintained and even enhanced as a result of this cannibalisation.
For C burning, the long-term effect of entrainment could be somewhat larger than for O burning due to the lower temperature threshold and the higher ratio ΔQ/2e int; for Si burning, the effect should be smaller. During earlier phases, our estimates break down because the convective flux carries only a small fraction of the energy generation by nuclear burning. If this is taken into account, the additional growth of convective regions due to entrainment is again of a modest scale (Spruit Reference Spruit2015).
5.5 Caveats
The estimates for the long-term effect of entrainment on the growth of convective regions in Section 5.4 are to be taken with caution, however. They are not only crude, time-integrated zeroth-order estimates; the entrainment law (36) is by no means set in stone. Current astrophysical 3D simulations only probe a limited range in the critical parameter RiB, and tend to suffer from insufficient resolution for high RiB, as shear instabilities develop on smaller and smaller scales.
As a result, it cannot be excluded that the entrainment law (35) transitions to a steeper slope in the astrophysically relevant regime of high RiB. Experiments also compete with the difficulties of a limited dynamic range in Reynolds, Prandtl, and Péclet number, and remain inconclusive about the regime of high RiB that obtains in stellar interiors. Power-law exponents larger than n = 1 (up to n = 7/4) have also been reported in this regime as alternatives to n = 1 (Fernando Reference Fernando1991; Strang & Fernando Reference Strang and Fernando2001; Fedorovich, Conzemius, & Mironov Reference Fedorovich, Conzemius and Mironov2004). A power-law exponent n > 1 would imply a strong suppression of entrainment in stellar interiors under most circumstances, and the long-term effect of entrainment would be negligible. Moreover, magnetic fields will affect the shear-driven instabilities responsible for convective boundary mixing (Brüggen & Hillebrandt Reference Brüggen and Hillebrandt2001).
Finally, most of the current 3D simulations of convective boundary mixing suffer from another potential problem; the balance between nuclear energy generation and neutrino cooling that obtains during quasi-stationary shell burning stages is typically violated, or neutrino cooling is not modelled at all. Jones et al. (Reference Jones, Andrassy, Sandalski, Davis, Woodward and Herwig2016b) pointed out that this may be problematic if neutrino cooling decelerates the buoyant convective plumes and reduces the shear velocity at the interfacial boundary. Only sufficiently long simulations will be able clarify whether the strong entrainment seen in some numerical simulations is robust or (partly) specific to a transient adjustment phase.
Thus, it remains to be seen whether convective boundary mixing has significant effects on the structure of supernova progenitors. Even if it does, it is not clear whether it will qualitatively affect the landscape of supernova progenitors. The general picture of the evolution of massive stars may stay well within the bounds of the variations that have been explored already, albeit in a more parametric way (see, e.g., Sukhbold & Woosley Reference Sukhbold and Woosley2014).
6 CONCLUSIONS
It is evident that our understanding of the supernova explosion mechanism has progressed considerably over the last few years. Whilst simulations of CCSNe have yet to demonstrate that they can correctly reproduce and explain the whole range explosions that is observed in nature, there are plenty of ideas for solving the remaining problems. Some important milestones from the last few years have been discussed in this paper, and can be summarised as follows:
-
• ECSN-like explosions of supernova progenitors with the lowest masses (
 $8\ldots 10\,\text{M}_\odot$
) can be modelled successfully both in 2D and in 3D. Regardless of the precise evolutionary channel from which they originate, supernovae from the transition region between the super-AGB star channel and classical iron-CCSNe share similar characteristics, i.e., low explosion energies of
$8\ldots 10\,\text{M}_\odot$
) can be modelled successfully both in 2D and in 3D. Regardless of the precise evolutionary channel from which they originate, supernovae from the transition region between the super-AGB star channel and classical iron-CCSNe share similar characteristics, i.e., low explosion energies of
 $\mathord {\sim }10^{50} \, {\rm erg}$
and small nickel masses of a few
$\mathord {\sim }10^{50} \, {\rm erg}$
and small nickel masses of a few
 $10^{-3}\,\text{M}_\odot$
. Due to the ejection of slightly neutron-rich material in the early ejecta, they are an interesting source site for the production of the lighter neutron-rich trans-iron elements (Sr, Y, Zr), and are potentially even a site for a weak r-process up to Ag and Pd (Wanajo et al. Reference Wanajo, Janka and Müller2011). An unambiguous identification of ECSN-like explosions amongst observed transients is still pending; however, although there are various candidate events.
$10^{-3}\,\text{M}_\odot$
. Due to the ejection of slightly neutron-rich material in the early ejecta, they are an interesting source site for the production of the lighter neutron-rich trans-iron elements (Sr, Y, Zr), and are potentially even a site for a weak r-process up to Ag and Pd (Wanajo et al. Reference Wanajo, Janka and Müller2011). An unambiguous identification of ECSN-like explosions amongst observed transients is still pending; however, although there are various candidate events. -
• Though it has yet to be demonstrated that the neutrino-driven explosion mechanism can robustly account for the explosions of more massive progenitors, first successful 3D models employing multi-group neutrino transport have recently become available. The reluctance of the first 3D models to develop explosions due to the different nature of turbulence in 3D proves to be no insurmountable setback; and even the unsuccessful 3D models computed so far appear to be close to explosion.
-
• Some of the recent 2D models produced by different groups (Summa et al. Reference Summa, Hanke, Janka, Melson, Marek and Müller2016; O’Connor & Couch Reference O’Connor and Couch2015) show similar results, which inspires some confidence that the simulations are now at a stage where modelling uncertainties due to different numerical methodologies are under reasonable control, though they have not been completely eliminated yet. We have addressed some of the sensitivities to the modelling assumption in this paper, including possible effects of numerical resolution as well as various aspects of the neutrino transport treatment.
-
• Recent studies have helped to unravel how the interplay between neutrino heating and hydrodynamic instabilities works quantitatively, and they have clarified why neutrino-driven mechanism can be obtained with a considerably smaller driving luminosity in multi-D.
-
• There is a number of ideas about missing physics that could make the neutrino-driven mechanism robust for a wider range of progenitors. These include rapid rotation (Nakamura et al. Reference Nakamura, Kuroda, Takiwaki and Kotake2014; Janka et al. Reference Janka, Melson and Summa2016; though stellar evolution makes this unlikely as a generic explanation), changes in the neutrino opacities (Melson et al. Reference Melson, Janka, Bollig, Hanke, Marek and Müller2015b), and a stronger forcing of non-radial instabilities due to seed perturbations from convective shell burning (Couch & Ott Reference Couch and Ott2013; Couch et al. Reference Couch, Chatzopoulos, Arnett and Timmes2015; Müller & Janka Reference Müller and Janka2015; Müller et al. Reference Müller, Viallet, Heger and Janka2016a).
-
• 3D initial conditions for supernova simulations have now become available (Couch et al. Reference Couch, Chatzopoulos, Arnett and Timmes2015; Müller et al. Reference Müller, Viallet, Heger and Janka2016a), and promise to play a significant and beneficial role in the explosion mechanism. A first 3D multi-group simulation starting from a 3D initial model of an
 $18\,\text{M}_\odot$
progenitor has been presented in this review. The model has already reached an explosion energy of 5 × 1050 erg, and suggests that the observed range of explosion energies may be within reach of 3D simulations.
$18\,\text{M}_\odot$
progenitor has been presented in this review. The model has already reached an explosion energy of 5 × 1050 erg, and suggests that the observed range of explosion energies may be within reach of 3D simulations. -
• Nonetheless, the study of 3D effects in supernova progenitors is yet in its infancy. A thorough exploration of the parameter space is required in order to judge whether they are generically important for our understanding of supernova explosions. This is not only true with regard to the 3D pre-collapse perturbations from shell burning that are crucial to the ‘perturbation-aided’ neutrino-driven mechanism. The role of convective boundary mixing on the structure of supernova progenitors also deserves to be explored.
Many of these developments are encouraging, though there are also hints of new uncertainties that may plague supernova theory in the future. Whether the new ideas of recent years will prove sufficient to explain shock revival in CCSNe remains to be seen. The perspectives are certainly good, but obviously a lot more remains to be done before simulations and theory can fully explain the diversity of core-collapse events in nature. There is no need to fear a shortage of fruitful scientific problems concerning the explosions of massive stars.
ACKNOWLEDGEMENTS
The author acknowledges fruitful discussions with R. Bollig, A. Burrows, S. Couch, E. Lentz, Th. Foglizzo, A. Heger, F. Herwig, W. R. Hix, H.-Th. Janka, S. Jones, T. Melson, R. Kotak, J. Murphy, K. Nomoto, E. O’Connor, L. Roberts, S. Smartt, H. Spruit, and M. Viallet. Particular thanks go to A. Heger, S. Jones, and K. Nomoto for providing density profiles of ECSN-like progenitors for Figure 1, to H.-Th. Janka for critical reading, and to T. Melson and M. Viallet for long-term assistance with the development of the Prometheus code. Part of this work has been supported by the Australian Research Council through a Discovery Early Career Researcher Award (grant DE150101145). This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. This work was also supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia, and by the National Science Foundation under Grant No. PHY-1430152 (JINA Center for the Evolution of the Elements). Computations were performed on the systems raijin (NCI) and Magnus (Pawsey), and also on the IBM iDataPlex system hydra at the Rechenzentrum of the Max-Planck Society (RZG) and at the Minnesota Supercomputing Institute.
A THE DENSITY GRADIENT IN THE POST-SHOCK REGION
Neglecting quadratic terms in the velocity and neglecting the self-gravity of the material in the gain region, one can write the momentum and energy equation for quasi-stationary accretion onto the proto-neutron star in the post-shock region as
in terms of the pressure P, the density ρ, the proto-neutron star mass M, the enthalpy h, the mass-specific net neutrino heating rate
![]() $\dot{q}_\nu$
, and the radial velocity
$\dot{q}_\nu$
, and the radial velocity
![]() $v_\text{r}$
. For a radiation-dominated gas, one has h ≈ 4P/ρ, which implies
$v_\text{r}$
. For a radiation-dominated gas, one has h ≈ 4P/ρ, which implies
and by taking ∂h/∂r from Equation (A2),
Solving for the local power-law slope α = ∂ln ρ/∂ln r of the density yields
Since
![]() $\dot{q}_\nu >0$
and
$\dot{q}_\nu >0$
and
![]() $v_\text{r}<0$
in the gain region before shock revival, this implies a power-law slope α that is no steeper than
$v_\text{r}<0$
in the gain region before shock revival, this implies a power-law slope α that is no steeper than










