1. Introduction
Accretion flows can be divided into several classes based on the accretion rate. The standard accretion disc model (Shakura & Sunyaev Reference Shakura and Sunyaev1973) which belongs to low regime cannot be applied to systems such as Sgr A* (Kato, Fukue, & Mineshige Reference Kato, Fukue and Mineshige2008). To explain the spectral energy distributions of accreting sources with very low and high accretion rates, respectively, the optically thin advection dominated accretion flows (ADAFs) (Ichimaru Reference Ichimaru1977; Narayan & Yi Reference Narayan and Yi1994) and slim discs (or optically thick ADAFs) (Abramowicz et al. Reference Abramowicz, Czerny, Lasota and Szuszkiewicz1988) were introduced. In these accretion flows, the energy released due to dissipation processes is not radiated away and is retained within the accreting fluid. Instead, this internal energy can be advected radially inward. ADAFs can be appropriate models to sources like the ultraluminous X-ray sources (Godet et al. Reference Godet2012; Mondal & Mukhopadhyay Reference Mondal and Mukhopadhyay2019), low-luminosity Active Galactic Nuclei (AGNs) (Park et al. Reference Park, Hada, Kino, Nakamura, Ro and Trippe2019; Younes et al. Reference Younes, Ptak, Ho, Xie, Terasima, Yuan, Huppenkothen and Yukita2019), narrow-line Seyfert 1 galaxies (Haba et al. Reference Haba, Terashima, Kunieda and Ohsuga2008; Meyer-Hofmeister & Meyer Reference Meyer-Hofmeister and Meyer2011), and Sgr A* (Yuan, Markoff, & Falcke Reference Yuan, Markoff and Falcke2002; Yuan & Narayan Reference Yuan and Narayan2014).
The numerical simulations have revealed that there exist considerable outflows in the optically thin or thick ADAFs (Ohsuga et al. Reference Ohsuga, Mineshige, Mori and Kato2009; Yuan, Bu, & Wu Reference Yuan, Bu and Wu2012b; Hashizume et al. Reference Hashizume, Ohsuga, Kawashima and Tanaka2015). This result has been confirmed by the observations of low-luminosity AGNs, Seyfert 1 galaxies, and X-ray binaries (Crenshaw & Kraemer Reference Crenshaw and Kraemer2012; Homan et al. Reference Homan, Neilsen, Allen, Chakrabarty, Fender, Fridriksson, Remillard and Schulz2016; Park et al. Reference Park, Hada, Kino, Nakamura, Ro and Trippe2019). The outflows by removing mass, angular momentum, and energy from the disc (Pudritz Reference Pudritz1985; Knigge Reference Knigge1999; Xue & Wang Reference Xue and Wang2005; Cao Reference Cao2016; Cao & Lai Reference Cao and Lai2019) can strongly affect the structure of accreting sources. For example, the gas can be pushed away from the disc surrounding the black hole by the outflows. This extraction causes the accretion rate of the black hole to decrease (Yuan et al. Reference Yuan, Yoon, Li, Gan, Ho and Guo2018; Bu & Yang Reference Bu and Yang2019). Blandford & Begelman (Reference Blandford and Begelman1999) by using a global analytical solution demonstrated that the radial dependence of the accretion rate is as a power-law function. Their power law index has been assumed to be in the range from 0 to 1. The numerical simulations have also shown that the accretion rate in the presence of outflows decreases as such a power-law function (e.g. Ohsuga et al. Reference Ohsuga, Mori, Nakamoto and Mineshige2005; Yuan et al. Reference Yuan, Bu and Wu2012b; 2012a; Bu et al. Reference Bu, Yuan, Wu and Cuadra2013; Yang et al. Reference Yang, Yuan, Ohsuga and Bu2014; Bu & Gan Reference Bu and Gan2018). Although recent theoretical studies showed that the power index can lie between 0.4 and 1.0 (Yuan, Wu, & Bu Reference Yuan, Wu and Bu2012a; Bu et al. Reference Bu, Yuan, Wu and Cuadra2013; Yang et al. Reference Yang, Yuan, Ohsuga and Bu2014), the observations of Sgr A* combined with the radiatively inefficient accretion model have predicted a range of  $0.3<s<0.4$ (Yuan, Quataert, & Narayan Reference Yuan, Quataert and Narayan2003).
$0.3<s<0.4$ (Yuan, Quataert, & Narayan Reference Yuan, Quataert and Narayan2003).
Different mechanisms have been suggested that drive the outflows (e.g. Chelouche & Netzer Reference Chelouche and Netzer2005; Ohsuga & Mineshige Reference Ohsuga and Mineshige2011; Cao Reference Cao2014; Yuan et al. Reference Yuan, Gan, Narayan, Sadowski, Bu and Bai2015; Hashizume et al. Reference Hashizume, Ohsuga, Kawashima and Tanaka2015). One of them can be large-scale magnetic fields (Blandford & Payne Reference Blandford and Payne1982; Igumenshchev, Narayan, & Abramowicz Reference Igumenshchev, Narayan and Abramowicz2003; Cao Reference Cao2014; Li & Cao Reference Li and Cao2019). The magnetic fields by transferring the angular momentum of a magnetized disc due to the magnetic braking (Stone & Norman Reference Stone and Norman1994) or magnetorotational instability (MRI) (Balbus & Hawley Reference Balbus and Hawley1998) can also modify the disc structure. Several attempts to examine the roles of outflows and large-scale magnetic fields in ADAFs have been made over the last several years. When large-scale magnetic fields with only toroidal component are considered, self-similar solutions indicate that this component of magnetic field rises the gas temperature of an ADAF with outflow (e.g. Abbassi, Ghanbari, & Ghasemnezhad Reference Abbassi, Ghanbari and Ghasemnezhad2010; Ghasemnezhad & Abbassi Reference Ghasemnezhad and Abbassi2016; Bu, Xu, & Zhu Reference Bu, Xu and Zhu2019; Reference Ghoreyshi and ShadmehriGhoreyshi & Shadmehri 2020). Such high temperatures do not match the values obtained from fitting the observational data of Seyfert galaxies (see Yuan & Zdziarski Reference Yuan and Zdziarski2004). Thus, the effect of other components of the field on the structure of ADAFs must be investigated. The influence of poloidal field component in an ADAF in the absence of outflows has been examined by Zhang & Dai (Reference Zhang and Dai2008). Adopting the ideal magnetohydrodynamic (MHD) approximation, they concluded that the poloidal field component can reduce the temperature (see also Ghasemnezhad Reference Ghasemnezhad2017). But Bu, Yuan, & Xie (Reference Bu, Yuan and Xie2009) showed that the role of poloidal field component in the temperature reduction can be more significant when the outflows are considered (see also Mosallanezhad, Khajavi, & Abbassi Reference Mosallanezhad, Khajavi and Abbassi2013).
Although most of the theoretical studies of accretion discs use the ideal MHD approximation, the resistive diffusion of magnetic field plays a key role in systems such as the protoplanetary (e.g. Sano, Inutsuka, & Miyama Reference Sano, Inutsuka and Miyama1998; Bai & Stone Reference Bai and Stone2013; Meheut et al. Reference Meheut, Fromang, Lesur, Joos and Longaretti2015; Flock et al. Reference Flock, Fromang, Turner and Benisty2017) and the dwarf nova (e.g. Gammie & Menou Reference Gammie and Menou1998; Sano & Stone Reference Sano and Stone2003; Scepi et al. Reference Scepi, Lesur, Dubus and Flock2018) discs. Numerical simulations have shown that the resistive dissipation can affect the growth rate and the saturation level of MRI (Fleming, Stone, & Hawley Reference Fleming, Stone and Hawley2000; Sano & Stone 2002a; Reference Sano and Stone2002b; Masada & Sano Reference Masada and Sano2008; Simon & Hawley Reference Simon and Hawley2009; Bai & Stone Reference Bai and Stone2013; Rodgers-Lee, Ray, & Downes Reference Rodgers-Lee, Ray and Downes2016) and also the rate of angular momentum transport (Ziegler & Rüdiger Reference Ziegler and Rüdiger2001; Fromang et al. Reference Fromang, Papaloizou, Lesur and Heinemann2007; Longaretti & Lesur Reference Longaretti and Lesur2010) in these systems. The importance of resistivity in other systems like the discs around Kerr black holes (Kudoh & Kaburaki Reference Kudoh and Kaburaki1996; Qian et al. Reference Qian, Fendt, Noble and Bugli2017; Qian et al. Reference Qian, Fendt and Vourellis2018; Shaghaghian Reference Shaghaghian2020), and even Sgr A* at the Galactic Center (e.g. Melia & Kowalenko Reference Melia and Kowalenko2001), has also been recognised. In hot accretion flows modelled for Sgr A*, the Coulomb coupling between ions and electrons is not strong enough. Since these flows, such as ADAFs, have the mean free path for Coulomb interactions larger than the typical size of the system, they are effectively collisionless (Quataert Reference Quataert1998), and the ideal MHD approximation may not be sufficient to study their properties. The recent studies have shown that the resistive dissipation in hot accretion flows around black holes can modify the amount of magnetic field, and the role of magnetic field in transferring the angular momentum (Zahra Zeraatgari et al. Reference Zahra Zeraatgari, Mosallanezhad, Abbassi and Yuan2018). Zahra Zeraatgari et al. (Reference Zahra Zeraatgari, Mosallanezhad, Abbassi and Yuan2018) suggested that the magnetic dissipation heating in regions of disc where outflows may be important is comparable to the viscous heating. Hence, the magnetic dissipation heating for increasing the electron temperature of ADAFs may be an effective agent (Bisnovatyi-Kogan & Lovelace Reference Bisnovatyi-Kogan and Lovelace1997; Ding, Yuan, & Liang Reference Ding, Yuan and Liang2010). On the other hand, the astrophysical outflows depend on the strength of magnetic diffusivity and type of the field component (Kuwabara et al. Reference Kuwabara, Shibata, Kudoh and Matsumoto2000; Fendt & Čemeljić Reference Fendt and Čemeljić2002; Igumenshchev et al. Reference Igumenshchev, Narayan and Abramowicz2003; Čemeljić, Vlahakis, & Tsinganos Reference Čemeljić, Vlahakis and Tsinganos2014; Qian, Fendt, & Vourellis Reference Qian, Fendt and Vourellis2018; Vourellis et al. Reference Vourellis, Fendt, Qian and Noble2019). Thus, one can expect that the structure of accretion discs is modified through the presence of resistive diffusion. Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012) showed when the resistive accretion flows with outflow is investigated, the disc has higher temperature due to magnetic diffusivity. Perhaps this result arises from considering a purely toroidal magnetic field. Although Abbassi & Mosallanezhad (Reference Abbassi and Mosallanezhad2012) studied the effect of other field components on the dynamics of resistive ADAFs, the role of outflows was neglected in their work. In the present paper, we shall extend the work of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012) by considering other field components. Indeed, our main aim is to investigate the roles of outflows and large-scale magnetic fields in restive ADAFs.
Here, the large-scale magnetic fields are assumed to have both z and  $\phi$ components. In order to study the effects of outflows and large-scale magnetic fields, we present the self-similar solutions of restive ADAFs. The paper is organized as follows. We first formulate basic equations for such a disc in Section 2 when outflows exist. In Section 3, the basic equations are solved using self-similar method and their results are discussed in Section 4. We then summarize our conclusions in final section.
$\phi$ components. In order to study the effects of outflows and large-scale magnetic fields, we present the self-similar solutions of restive ADAFs. The paper is organized as follows. We first formulate basic equations for such a disc in Section 2 when outflows exist. In Section 3, the basic equations are solved using self-similar method and their results are discussed in Section 4. We then summarize our conclusions in final section.
2. Basic equations
To investigate the structure of resistive ADAFs, we first write the basic equations in the cylindrical coordinate system  $(r,\phi, z)$ centred on the central object. The accretion disc is assumed to be stationary (
$(r,\phi, z)$ centred on the central object. The accretion disc is assumed to be stationary ( $\partial/\partial t=0$) and axisymmetric (
$\partial/\partial t=0$) and axisymmetric ( $\partial/\partial\phi=0$). All flow variables are considered to be a function only of r. We have ignored the relativistic effects and used Newtonian gravity. Although the dominant component of magnetic field in the main disc body, inner torus, and corona is in the
$\partial/\partial\phi=0$). All flow variables are considered to be a function only of r. We have ignored the relativistic effects and used Newtonian gravity. Although the dominant component of magnetic field in the main disc body, inner torus, and corona is in the  $\phi$-direction, the magnetic field near the poles may be poloidal, especially with the vertical component (Hirose et al. Reference Hirose, Krolik, De Villiers and Hawley2004). Therefore, we adopt a large-scale magnetic field with the components
$\phi$-direction, the magnetic field near the poles may be poloidal, especially with the vertical component (Hirose et al. Reference Hirose, Krolik, De Villiers and Hawley2004). Therefore, we adopt a large-scale magnetic field with the components  $B_\phi$ and
$B_\phi$ and  $B_z$ and neglect the radial component
$B_z$ and neglect the radial component  $B_r$. Hence, the basic equations of our model are written as
$B_r$. Hence, the basic equations of our model are written as
 \begin{equation}\frac{\rm d}{{\rm d}r} (r \Sigma V_r)+\frac{1}{2\pi} \frac{{\rm d} \dot{M}_W}{\rm dr}=0,\end{equation}
\begin{equation}\frac{\rm d}{{\rm d}r} (r \Sigma V_r)+\frac{1}{2\pi} \frac{{\rm d} \dot{M}_W}{\rm dr}=0,\end{equation} \begin{align}V_r \frac{{\rm d} V_r}{{\rm d}r} = & \frac{{V_\phi}^2}{r}-\frac{GM_*}{r^2}-\frac{1}{\Sigma}\frac{{\rm d}}{{\rm d}r}\left(\Sigma c_s^2\right)\nonumber\\[4pt]& -\frac{1}{2\Sigma}\frac{{\rm d}}{{\rm d}r}\Big(\Sigma \left({c_\phi}^2+{c_z}^2\right)\Big)-\frac{{c_\phi}^2}{r},\end{align}
\begin{align}V_r \frac{{\rm d} V_r}{{\rm d}r} = & \frac{{V_\phi}^2}{r}-\frac{GM_*}{r^2}-\frac{1}{\Sigma}\frac{{\rm d}}{{\rm d}r}\left(\Sigma c_s^2\right)\nonumber\\[4pt]& -\frac{1}{2\Sigma}\frac{{\rm d}}{{\rm d}r}\Big(\Sigma \left({c_\phi}^2+{c_z}^2\right)\Big)-\frac{{c_\phi}^2}{r},\end{align} \begin{equation}\frac{V_r}{r} \frac{{\rm d}}{{\rm d}r} \left(r V_{\phi}\right)=\frac{1}{r^2\Sigma}\frac{{\rm d}}{{\rm d}r}\left( r^3\nu\Sigma \frac{{\rm d}\Omega}{{\rm d}r}\right)-\frac{\ell^2 \Omega }{2\pi\Sigma} \frac{{\rm d}\dot{M}_W}{{\rm d}r},\end{equation}
\begin{equation}\frac{V_r}{r} \frac{{\rm d}}{{\rm d}r} \left(r V_{\phi}\right)=\frac{1}{r^2\Sigma}\frac{{\rm d}}{{\rm d}r}\left( r^3\nu\Sigma \frac{{\rm d}\Omega}{{\rm d}r}\right)-\frac{\ell^2 \Omega }{2\pi\Sigma} \frac{{\rm d}\dot{M}_W}{{\rm d}r},\end{equation} \begin{equation}\frac{\Sigma V_r}{\gamma-1}\frac{{\rm d} c_s^2}{{\rm d}r}-2HV_r c_s^2\frac{{\rm d}\rho}{{\rm d}r}=f(Q_{\rm vis}+Q_B)-Q_W,\end{equation}
\begin{equation}\frac{\Sigma V_r}{\gamma-1}\frac{{\rm d} c_s^2}{{\rm d}r}-2HV_r c_s^2\frac{{\rm d}\rho}{{\rm d}r}=f(Q_{\rm vis}+Q_B)-Q_W,\end{equation} \begin{equation}\dot{B}_\phi=-\frac{{\rm d}}{{\rm d}r}(V_r B_\phi)+\eta\frac{{\rm d}}{{\rm d}r}\left(\frac{1}{r}\frac{{\rm d}}{{\rm d}r}(rB_\phi)\right),\end{equation}
\begin{equation}\dot{B}_\phi=-\frac{{\rm d}}{{\rm d}r}(V_r B_\phi)+\eta\frac{{\rm d}}{{\rm d}r}\left(\frac{1}{r}\frac{{\rm d}}{{\rm d}r}(rB_\phi)\right),\end{equation} \begin{equation}\dot{B}_z=-\frac{1}{r}\frac{{\rm d}}{{\rm d}r}(rV_r B_z)+\frac{\eta}{r}\frac{{\rm d}}{{\rm d}r}\left(r\frac{{\rm d}B_z}{{\rm d}r}\right),\end{equation}
\begin{equation}\dot{B}_z=-\frac{1}{r}\frac{{\rm d}}{{\rm d}r}(rV_r B_z)+\frac{\eta}{r}\frac{{\rm d}}{{\rm d}r}\left(r\frac{{\rm d}B_z}{{\rm d}r}\right),\end{equation}
where the surface density  $\Sigma$ is defined as
$\Sigma$ is defined as  $\Sigma=2\rho H$, and
$\Sigma=2\rho H$, and  $\rho$ is the midplane density of the disc. Here, the radial infall velocity and the rotational velocity of the disc are denoted as
$\rho$ is the midplane density of the disc. Here, the radial infall velocity and the rotational velocity of the disc are denoted as  $V_r({<}0)$ and
$V_r({<}0)$ and  $V_\phi(=r\Omega)$, respectively.
$V_\phi(=r\Omega)$, respectively.  $\dot{B}_{\phi,z}$ are the field escaping/creating rate which may be due to the magnetic diffusion or dynamo effect (Oda et al. Reference Oda, Machida, Nakamura and Matsumoto2007). The sound speed
$\dot{B}_{\phi,z}$ are the field escaping/creating rate which may be due to the magnetic diffusion or dynamo effect (Oda et al. Reference Oda, Machida, Nakamura and Matsumoto2007). The sound speed  $c_s$ and the Alfvén sound speeds
$c_s$ and the Alfvén sound speeds  $c_{\phi,z}$ are also defined as
$c_{\phi,z}$ are also defined as
 \begin{equation*}{c_s}^2=p/\rho, {c_{\phi,z}}^2={B_{\phi,z}}^2/ 4\pi\rho,\end{equation*}
\begin{equation*}{c_s}^2=p/\rho, {c_{\phi,z}}^2={B_{\phi,z}}^2/ 4\pi\rho,\end{equation*}
where p is the gas pressure in the disc. The hydrostatic balance in the vertical direction leads to a relation between H and  $c_{s,\phi}$. We have
$c_{s,\phi}$. We have
 \begin{equation}\frac{GM_*}{r^3}H^2={c_s}^2(1+\beta_\phi).\end{equation}
\begin{equation}\frac{GM_*}{r^3}H^2={c_s}^2(1+\beta_\phi).\end{equation}
Here,  $M_*$ is the mass of the central object. In this paper, we use definitions
$M_*$ is the mass of the central object. In this paper, we use definitions  $\beta_{\phi,z}=(1/2)(c_{\phi,z}/c_s)^2$. For the hot accretion flows, the typical values of
$\beta_{\phi,z}=(1/2)(c_{\phi,z}/c_s)^2$. For the hot accretion flows, the typical values of  $\beta_\phi$ and
$\beta_\phi$ and  $\beta_z$ may be between 0.01 and 1 (e.g. De Villiers, Hawley, & Krolik Reference De Villiers, Hawley and Krolik2003; Beckwith, Hawley, & Krolik Reference Beckwith, Hawley and Krolik2008). However, the numerical simulations indicate that the accretion flows in the hot accretion disc change from a gas pressure-supported state to a magnetically supported state as soon as the thermal instability arises (Machida, Nakamura, & Matsumoto Reference Machida, Nakamura and Matsumoto2006). Under these conditions, one would expect that
$\beta_z$ may be between 0.01 and 1 (e.g. De Villiers, Hawley, & Krolik Reference De Villiers, Hawley and Krolik2003; Beckwith, Hawley, & Krolik Reference Beckwith, Hawley and Krolik2008). However, the numerical simulations indicate that the accretion flows in the hot accretion disc change from a gas pressure-supported state to a magnetically supported state as soon as the thermal instability arises (Machida, Nakamura, & Matsumoto Reference Machida, Nakamura and Matsumoto2006). Under these conditions, one would expect that  $\beta_\phi$ and
$\beta_\phi$ and  $\beta_z$ exceed unity. Hence, we shall also consider the cases with values greater than 1.
$\beta_z$ exceed unity. Hence, we shall also consider the cases with values greater than 1.
The mass-loss rate by outflow  $\dot{M}_W$ is
$\dot{M}_W$ is
 \begin{equation}\dot{M}_W(r)=\int 4\pi r'\dot{m}_W(r') {\rm d}r',\end{equation}
\begin{equation}\dot{M}_W(r)=\int 4\pi r'\dot{m}_W(r') {\rm d}r',\end{equation}
where  $\dot{m}_W$ is the mass loss rate per unit area from each disc face. The definition of the accretion rate, i.e.
$\dot{m}_W$ is the mass loss rate per unit area from each disc face. The definition of the accretion rate, i.e.  $\dot{M}=-2\pi r\Sigma V_r$, and Equation (1) can result in
$\dot{M}=-2\pi r\Sigma V_r$, and Equation (1) can result in
 \begin{equation}\frac{{\rm d} \dot{M}}{{\rm d}r}=\frac{{\rm d} \dot{M}_W}{{\rm d}r}.\end{equation}
\begin{equation}\frac{{\rm d} \dot{M}}{{\rm d}r}=\frac{{\rm d} \dot{M}_W}{{\rm d}r}.\end{equation}
If the radial dependence of  $\dot{M}$ is
$\dot{M}$ is  $\dot{M}_0(\frac{r}{r_0})^s$ (Blandford & Begelman Reference Blandford and Begelman1999) where
$\dot{M}_0(\frac{r}{r_0})^s$ (Blandford & Begelman Reference Blandford and Begelman1999) where  $\dot{M}_0$ is the mass accretion rate at the outer boundary
$\dot{M}_0$ is the mass accretion rate at the outer boundary  $r_0$, we have
$r_0$, we have
 \begin{equation}\dot{m}_W=\frac{s}{4\pi r_0^2}\dot{M}_0\left(\frac{r}{r_0}\right)^{s-2}.\end{equation}
\begin{equation}\dot{m}_W=\frac{s}{4\pi r_0^2}\dot{M}_0\left(\frac{r}{r_0}\right)^{s-2}.\end{equation}
Here, s represents the outflow strength in the disc. Note that  $s = 0$ corresponds to a disc without winds.
$s = 0$ corresponds to a disc without winds.
The last term of right-hand side in Equation (3) represents the angular momentum extracted by the wind where  $\ell$ is the length of the lever arm. In the present paper,
$\ell$ is the length of the lever arm. In the present paper,  $\ell$ is assumed to be equal to 1 describing the case in which outflowing material carries away the specific angular momentum it had at the point of ejection (Knigge Reference Knigge1999). The cases with
$\ell$ is assumed to be equal to 1 describing the case in which outflowing material carries away the specific angular momentum it had at the point of ejection (Knigge Reference Knigge1999). The cases with  $\ell < 1$ (or
$\ell < 1$ (or  $>1$) are expected to describe the outflows that carry away less (or more) angular momentum.
$>1$) are expected to describe the outflows that carry away less (or more) angular momentum.
In the energy Equation (4), the advection factor f lying between 0 and 1 is defined as  $f =1 - \big(Q_{\rm rad}/Q^{+}\big)$ in which
$f =1 - \big(Q_{\rm rad}/Q^{+}\big)$ in which  $Q^{+}=Q_{\rm vis}+Q_B$. Here,
$Q^{+}=Q_{\rm vis}+Q_B$. Here,  $Q_{\rm rad}$,
$Q_{\rm rad}$,  $Q_{\rm vis}$, and
$Q_{\rm vis}$, and  $Q_B$ are the radiative cooling rate, the viscous heating rate, and the resistive heating rate, respectively. The viscous and resistive heating rates, respectively, are
$Q_B$ are the radiative cooling rate, the viscous heating rate, and the resistive heating rate, respectively. The viscous and resistive heating rates, respectively, are
 \begin{equation*}Q_{\rm vis}=\nu\Sigma\left(r\frac{{\rm d} \Omega}{{\rm d}r}\right)^2,\end{equation*}
\begin{equation*}Q_{\rm vis}=\nu\Sigma\left(r\frac{{\rm d} \Omega}{{\rm d}r}\right)^2,\end{equation*}and
 \begin{equation*}Q_B=\frac{H\eta}{2\pi}\mid\nabla\times\mathbf{B}\mid^2.\end{equation*}
\begin{equation*}Q_B=\frac{H\eta}{2\pi}\mid\nabla\times\mathbf{B}\mid^2.\end{equation*}
Note that f in the advection-dominated regime is equal to unity. In order to obtain the energy loss due to outflow, the wind is assumed to be driven from the disc surface. If some of the energy generated by viscosity (or any other mechanism) in the disc may power the wind, it must supply some or all of the wind’s binding and kinetic energies. Knigge (Reference Knigge1999) showed that the energy loss by outflow  $Q_W$ is defined by
$Q_W$ is defined by
 \begin{equation*}Q_W=\frac{1}{2}\zeta\dot{m}_W {V_K}^2,\end{equation*}
\begin{equation*}Q_W=\frac{1}{2}\zeta\dot{m}_W {V_K}^2,\end{equation*}
where  $V_K$ (
$V_K$ ( $=r\Omega_K=\sqrt{GM_*/r}$) is the Keplerian speed and the efficiency factor
$=r\Omega_K=\sqrt{GM_*/r}$) is the Keplerian speed and the efficiency factor  $\zeta$ may be a function of
$\zeta$ may be a function of  $\ell$. The efficiency factor for a case with
$\ell$. The efficiency factor for a case with  $\ell=1$ is equal to 1 (Knigge Reference Knigge1999).
$\ell=1$ is equal to 1 (Knigge Reference Knigge1999).
The magnetic diffusivity  $\eta$ is assumed to be
$\eta$ is assumed to be
 \begin{equation}\eta=\frac{\nu}{P_m}=\frac{\alpha c_s H}{P_m}.\end{equation}
\begin{equation}\eta=\frac{\nu}{P_m}=\frac{\alpha c_s H}{P_m}.\end{equation}
Here,  $P_m$ is the magnetic Prandtl number. Although the magnetic Prandtl number is generally considered to be a constant, its value depends on the disc radius (Balbus & Henri Reference Balbus and Henri2008). The studies show that the magnetic Prandtl number may lie in the range from
$P_m$ is the magnetic Prandtl number. Although the magnetic Prandtl number is generally considered to be a constant, its value depends on the disc radius (Balbus & Henri Reference Balbus and Henri2008). The studies show that the magnetic Prandtl number may lie in the range from  $10^{-3}$ to
$10^{-3}$ to  $10^3$ in the discs around compact X-ray sources and AGNs (Balbus & Henri Reference Balbus and Henri2008). Note that we use the
$10^3$ in the discs around compact X-ray sources and AGNs (Balbus & Henri Reference Balbus and Henri2008). Note that we use the  $\alpha$-prescription of Shakura & Sunyaev (Reference Shakura and Sunyaev1973) for the kinematic viscosity coefficient
$\alpha$-prescription of Shakura & Sunyaev (Reference Shakura and Sunyaev1973) for the kinematic viscosity coefficient  $\nu$.
$\nu$.
3. Self-similar solutions
In this paper, some of parameters such as the magnetic Prandtl number are assumed to be a constant for simplicity. We employ a self-similar treatment similar to Shadmehri (Reference Shadmehri2008) and Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012). Our self-similar solutions are
 \begin{equation}\Sigma(r)=C_0\Sigma_0\left(\frac{r}{r_0}\right)^{s-\frac{1}{2}},\end{equation}
\begin{equation}\Sigma(r)=C_0\Sigma_0\left(\frac{r}{r_0}\right)^{s-\frac{1}{2}},\end{equation} \begin{equation}V_r(r)=-C_1\sqrt{\frac{GM_*}{r_0}}\left(\frac{r}{r_0}\right)^{-1/2},\end{equation}
\begin{equation}V_r(r)=-C_1\sqrt{\frac{GM_*}{r_0}}\left(\frac{r}{r_0}\right)^{-1/2},\end{equation} \begin{equation}V_{\phi}(r)=C_2\sqrt{\frac{GM_*}{r_0}}\left(\frac{r}{r_0}\right)^{-1/2},\end{equation}
\begin{equation}V_{\phi}(r)=C_2\sqrt{\frac{GM_*}{r_0}}\left(\frac{r}{r_0}\right)^{-1/2},\end{equation} \begin{equation}c_s^2(r)=C_3\frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation}
\begin{equation}c_s^2(r)=C_3\frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation} \begin{equation}c_{\phi}^2(r)=2\beta_{\phi} C_3 \frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation}
\begin{equation}c_{\phi}^2(r)=2\beta_{\phi} C_3 \frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation} \begin{equation}c_{z}^2(r)=2\beta_{z} C_3 \frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation}
\begin{equation}c_{z}^2(r)=2\beta_{z} C_3 \frac{GM_*}{r_0}\left(\frac{r}{r_0}\right)^{-1},\end{equation} \begin{equation}H(r)=C_4 r_0\left(\frac{r}{r_0}\right),\end{equation}
\begin{equation}H(r)=C_4 r_0\left(\frac{r}{r_0}\right),\end{equation}
where  $\Sigma_0$ and
$\Sigma_0$ and  $r_0$ are denoted to provide the non-dimensional form of equations. By substituting the self-similar solutions (19)–(18) into the basic Equations (1)–(4) and (7), we have
$r_0$ are denoted to provide the non-dimensional form of equations. By substituting the self-similar solutions (19)–(18) into the basic Equations (1)–(4) and (7), we have
 \begin{equation}-C_0 C_1+\dot{m}=0,\end{equation}
\begin{equation}-C_0 C_1+\dot{m}=0,\end{equation} \begin{equation}-\frac{1}{2}{C_1}^2={C_2}^2-1-\left(s-\frac{3}{2}\right)\left(1+\beta_{\phi}+\beta_{z}\right)C_3-2\beta_{\phi}C_3,\end{equation}
\begin{equation}-\frac{1}{2}{C_1}^2={C_2}^2-1-\left(s-\frac{3}{2}\right)\left(1+\beta_{\phi}+\beta_{z}\right)C_3-2\beta_{\phi}C_3,\end{equation} $${C_1}{\rm{ }} = 3\alpha \left( {s + {1 \over 2}} \right)\sqrt {{C_3}} {C_4} + {{2s{\ell ^2}\dot m} \over {{C_0}}},$$
$${C_1}{\rm{ }} = 3\alpha \left( {s + {1 \over 2}} \right)\sqrt {{C_3}} {C_4} + {{2s{\ell ^2}\dot m} \over {{C_0}}},$$ $$\eqalign{
& \left( {{1 \over {\gamma - 1}} + s - {3 \over 2}} \right){C_1}{C_3} = f\alpha \sqrt {{C_3}} {C_4}\left( {{9 \over 4}{C_2}^2} \right.\qquad \cr
& \left. { + {1 \over {2{P_m}}}\left( {{\beta _\phi }{{\left( {s - {1 \over 2}} \right)}^2} + {\beta _z}{{\left( {s - {5 \over 2}} \right)}^2}} \right){C_3}} \right) - {{s\zeta \dot m} \over {4{C_0}}}, \cr} $$
$$\eqalign{
& \left( {{1 \over {\gamma - 1}} + s - {3 \over 2}} \right){C_1}{C_3} = f\alpha \sqrt {{C_3}} {C_4}\left( {{9 \over 4}{C_2}^2} \right.\qquad \cr
& \left. { + {1 \over {2{P_m}}}\left( {{\beta _\phi }{{\left( {s - {1 \over 2}} \right)}^2} + {\beta _z}{{\left( {s - {5 \over 2}} \right)}^2}} \right){C_3}} \right) - {{s\zeta \dot m} \over {4{C_0}}}, \cr} $$ \begin{equation}{C_4}^2=C_3(1+\beta_{\phi}),\end{equation}
\begin{equation}{C_4}^2=C_3(1+\beta_{\phi}),\end{equation}
where the non-dimensional mass accretion rate  $\dot{m}$ is defined as
$\dot{m}$ is defined as  $\dot{M}_0/(2\pi r_0 \Sigma_0 \sqrt{GM_*/r_0})$. After some algebraic manipulations, a fourth-order algebraic equation is obtained for
$\dot{M}_0/(2\pi r_0 \Sigma_0 \sqrt{GM_*/r_0})$. After some algebraic manipulations, a fourth-order algebraic equation is obtained for  $C_4$:
$C_4$:
 \begin{align} & \dfrac{81f\alpha^2\left(s+\frac{1}{2}\right)^2}{8(1+\beta_{\phi})(1-2s\ell^2)^2}{C_4}^4+\left[\frac{3\left(s+\frac{1}{2}\right)}{(1+\beta_{\phi})(1-2s\ell^2)}\left(\frac{1}{\gamma-1}+s-\frac{3}{2}\right)\right.\nonumber\\[7pt]&\quad -\frac{9f}{4(1+\beta_{\phi})}\left( \left(s+\frac{3}{2}\right)(1+\beta_{\phi}+\beta_{z})+2\beta_{\phi} \right)\nonumber\\[7pt]&\quad\left. -\frac{f}{2P_m(1+\beta_{\phi})} \left( \beta_{\phi}\left(s-\frac{1}{2}\right)^2+\beta_{z}\left(s-\frac{5}{2}\right)^2 \right) \right]{C_4}^2\nonumber\\[7pt]&\quad -\dfrac{9}{4}f+\dfrac{3s\zeta(s+\frac{1}{2})}{4(1-2s\ell^2)}=0.\end{align}
\begin{align} & \dfrac{81f\alpha^2\left(s+\frac{1}{2}\right)^2}{8(1+\beta_{\phi})(1-2s\ell^2)^2}{C_4}^4+\left[\frac{3\left(s+\frac{1}{2}\right)}{(1+\beta_{\phi})(1-2s\ell^2)}\left(\frac{1}{\gamma-1}+s-\frac{3}{2}\right)\right.\nonumber\\[7pt]&\quad -\frac{9f}{4(1+\beta_{\phi})}\left( \left(s+\frac{3}{2}\right)(1+\beta_{\phi}+\beta_{z})+2\beta_{\phi} \right)\nonumber\\[7pt]&\quad\left. -\frac{f}{2P_m(1+\beta_{\phi})} \left( \beta_{\phi}\left(s-\frac{1}{2}\right)^2+\beta_{z}\left(s-\frac{5}{2}\right)^2 \right) \right]{C_4}^2\nonumber\\[7pt]&\quad -\dfrac{9}{4}f+\dfrac{3s\zeta(s+\frac{1}{2})}{4(1-2s\ell^2)}=0.\end{align}
We are able to determine easily other flow quantities as a function of  $C_4$. Their dependence on
$C_4$. Their dependence on  $C_4$ is
$C_4$ is
 \begin{equation}C_0=\frac{\sqrt{1+\beta_{\phi}}\left(1-2s\ell^2\right)}{3\alpha\left(s+\frac{1}{2}\right)}\dot{m}{C_4}^{-2},\end{equation}
\begin{equation}C_0=\frac{\sqrt{1+\beta_{\phi}}\left(1-2s\ell^2\right)}{3\alpha\left(s+\frac{1}{2}\right)}\dot{m}{C_4}^{-2},\end{equation} \begin{equation}C_1=\frac{3\alpha\left(s+\frac{1}{2}\right)}{(1-2s\ell^2)\sqrt{1+\beta_{\phi}}}{C_4}^2,\end{equation}
\begin{equation}C_1=\frac{3\alpha\left(s+\frac{1}{2}\right)}{(1-2s\ell^2)\sqrt{1+\beta_{\phi}}}{C_4}^2,\end{equation} \begin{align}C_2 = & \Bigg\{ 1+\frac{1}{1+\beta_{\phi}}\Big[ \left(s-\frac{3}{2}\right)(1+\beta_{\phi}+\beta_{z})+2\beta_{\phi} \Big]{C_4}^2\nonumber\\[5pt]& -\frac{9\alpha^2\left(s+\frac{1}{2}\right)^2}{2(1+\beta_{\phi})(1-2s\ell^2)^2}{C_4}^4 \Bigg\}^{1/2},\end{align}
\begin{align}C_2 = & \Bigg\{ 1+\frac{1}{1+\beta_{\phi}}\Big[ \left(s-\frac{3}{2}\right)(1+\beta_{\phi}+\beta_{z})+2\beta_{\phi} \Big]{C_4}^2\nonumber\\[5pt]& -\frac{9\alpha^2\left(s+\frac{1}{2}\right)^2}{2(1+\beta_{\phi})(1-2s\ell^2)^2}{C_4}^4 \Bigg\}^{1/2},\end{align} \begin{equation}C_3=\frac{1}{1+\beta_{\phi}}{C_4}^2.\end{equation}
\begin{equation}C_3=\frac{1}{1+\beta_{\phi}}{C_4}^2.\end{equation}
When the large-scale magnetic field has only the toroidal component, Equation (24) and the similarity solutions (25)–(28) reduce to results of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012). In the absence of magnetic diffusivity, one can obtain the findings of Mosallanezhad et al. (Reference Mosallanezhad, Khajavi and Abbassi2013) without the radial field component. By setting  $\beta_{\phi}=\beta_z=0$, our solutions tend to the solutions presented by Shadmehri (Reference Shadmehri2008) when thermal conduction is ignored.
$\beta_{\phi}=\beta_z=0$, our solutions tend to the solutions presented by Shadmehri (Reference Shadmehri2008) when thermal conduction is ignored.
4. Results
In order to examine the effects of outflows and large-scale magnetic field on the properties of a resistive ADAF, we solve the Equation (24) numerically. To investigate the disc properties physically, only real roots corresponding to positive  ${C_2}^2$ must be adopted. We illustrate the disc variables as a function of inverse magnetic Prandtl number, i.e.,
${C_2}^2$ must be adopted. We illustrate the disc variables as a function of inverse magnetic Prandtl number, i.e.,  ${P_m}^{-1}$. In this paper, the magnetic Prandtl number is assumed to be in the range from 0.1 to 10 (Lesur & Longaretti Reference Lesur and Longaretti2007). Note that the MRI in this range is exited (Käpylä & Korpi Reference Käpylä and Korpi2011). We also set
${P_m}^{-1}$. In this paper, the magnetic Prandtl number is assumed to be in the range from 0.1 to 10 (Lesur & Longaretti Reference Lesur and Longaretti2007). Note that the MRI in this range is exited (Käpylä & Korpi Reference Käpylä and Korpi2011). We also set  $\dot{m}=0.1$,
$\dot{m}=0.1$,  $f =\ell=\zeta=1$,
$f =\ell=\zeta=1$,  $\gamma=4/3$,
$\gamma=4/3$,  $\alpha =0.1$,
$\alpha =0.1$,  $\beta_\phi=\beta_z=1.0$, and
$\beta_\phi=\beta_z=1.0$, and  $s=0.2$ unless otherwise is stated.
$s=0.2$ unless otherwise is stated.
In Figure 1, the behaviour of physical variables versus  ${P_m}^{-1}$ is illustrated for different values of the power law index s. According to the momentum conservation, the term
${P_m}^{-1}$ is illustrated for different values of the power law index s. According to the momentum conservation, the term  $1-2s\ell^2$ must be greater than zero (see also Equation (25)). Hence, the value of s for a disc with
$1-2s\ell^2$ must be greater than zero (see also Equation (25)). Hence, the value of s for a disc with  $\ell=1$ lies between 0 and 1/2. Since the power law index s for a case with
$\ell=1$ lies between 0 and 1/2. Since the power law index s for a case with  $\alpha=0.1$ cannot be greater than 0.4 (Yang et al. Reference Yang, Yuan, Ohsuga and Bu2014), we assume that the value of s is in the range of 0.0 (a case without outflow) to 0.3 (a case with moderate outflow). In top left panel, the dimensionless thickness of disc
$\alpha=0.1$ cannot be greater than 0.4 (Yang et al. Reference Yang, Yuan, Ohsuga and Bu2014), we assume that the value of s is in the range of 0.0 (a case without outflow) to 0.3 (a case with moderate outflow). In top left panel, the dimensionless thickness of disc  $H/r$ is illustrated. In the present paper, the outflows are assumed to extract the energy from the disc. The removal of energy by outflows reduces the disc temperature. According to Equation (28), the presence of outflows causes the disc thickness to decrease as revealed through previous numerical calculations (e.g. Faghei & Mollatayefeh Reference Faghei and Mollatayefeh2012; Reference Ghoreyshi and ShadmehriGhoreyshi & Shadmehri 2020). The ratio of
$H/r$ is illustrated. In the present paper, the outflows are assumed to extract the energy from the disc. The removal of energy by outflows reduces the disc temperature. According to Equation (28), the presence of outflows causes the disc thickness to decrease as revealed through previous numerical calculations (e.g. Faghei & Mollatayefeh Reference Faghei and Mollatayefeh2012; Reference Ghoreyshi and ShadmehriGhoreyshi & Shadmehri 2020). The ratio of  $H/r$ rises with decreasing the magnetic Prandtl number. This means that an increase in the magnetic diffusivity, and therefore in the resistive heating, can lead to a higher gas temperature. Consequently, the enhancement of the gas temperature can puff up the accretion disc and the disc gets thicker. Noting that the
$H/r$ rises with decreasing the magnetic Prandtl number. This means that an increase in the magnetic diffusivity, and therefore in the resistive heating, can lead to a higher gas temperature. Consequently, the enhancement of the gas temperature can puff up the accretion disc and the disc gets thicker. Noting that the  $C_4$-dependence of density in Equation (25), we also find that the surface density of the disc reaches a maximum value at the highest adopted value of
$C_4$-dependence of density in Equation (25), we also find that the surface density of the disc reaches a maximum value at the highest adopted value of  $P_m$. In the high-
$P_m$. In the high- $P_m$ limit, the surface density of a disc without outflow is more than that in a disc with moderate wind. Indeed, the outflows by extracting the disc material can lead to a reduction in the surface density. When the limit of small-
$P_m$ limit, the surface density of a disc without outflow is more than that in a disc with moderate wind. Indeed, the outflows by extracting the disc material can lead to a reduction in the surface density. When the limit of small- $P_m$ is considered, however, the surface density of the disc in the absence of outflows becomes less. At
$P_m$ is considered, however, the surface density of the disc in the absence of outflows becomes less. At  $P_m=0.5$, e.g. the surface density for a case
$P_m=0.5$, e.g. the surface density for a case  $s=0.3$ is about twice the value in
$s=0.3$ is about twice the value in  $s=0.0$. But Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012) showed that the net effect of the outflow on the surface density is independent of the magnetic Prandtl number. We find that such a difference in results is due to the presence of vertical component of magnetic field. The reason is as follows. According to Equation (22), the radial velocity depends sensitively on the vertical magnetic field and the magnetic Prandtl number (see also the profile of the infall velocity in Figure 3). The dependence of the surface density on the infall velocity (Equation (19)) leads to such a trend for the density profile.
$s=0.0$. But Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012) showed that the net effect of the outflow on the surface density is independent of the magnetic Prandtl number. We find that such a difference in results is due to the presence of vertical component of magnetic field. The reason is as follows. According to Equation (22), the radial velocity depends sensitively on the vertical magnetic field and the magnetic Prandtl number (see also the profile of the infall velocity in Figure 3). The dependence of the surface density on the infall velocity (Equation (19)) leads to such a trend for the density profile.

Figure 1. Profiles of the physical variables of the accretion disc versus for different values of s, as labeled. It is assumed that and  $\alpha=0.1$,
$\alpha=0.1$,  $\ \beta_{\phi}=\beta_z=1.0$,
$\ \beta_{\phi}=\beta_z=1.0$,  $\zeta=\ell=f=1.0$.
$\zeta=\ell=f=1.0$.
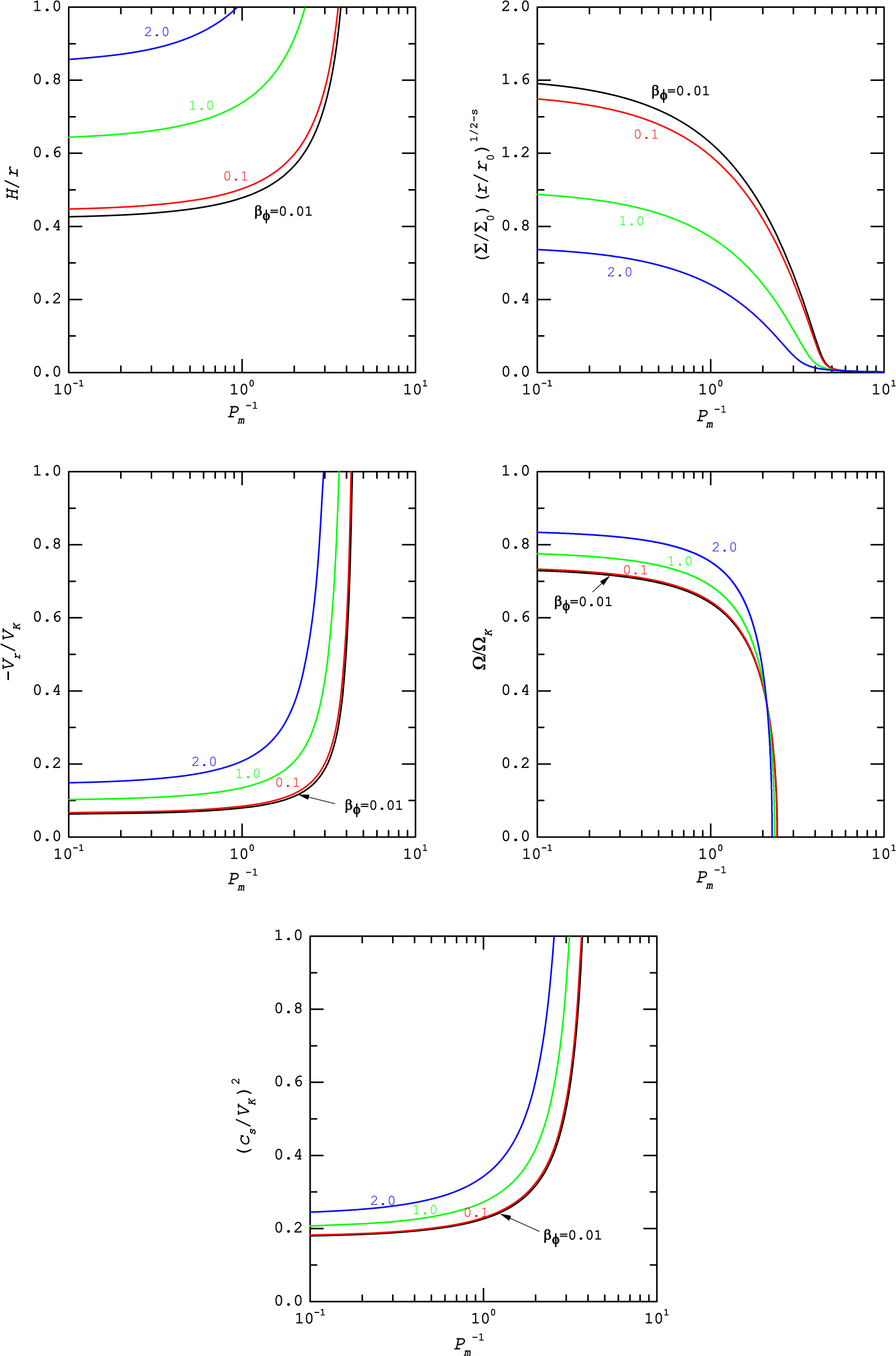
Figure 2. Similar to Figure 1, but for  $s=0.2$ and different values of
$s=0.2$ and different values of  $\beta_{\phi}$ (as labelled).
$\beta_{\phi}$ (as labelled).

Figure 3. Similar to Figure 1, but for  $s=0.2$ and different values of
$s=0.2$ and different values of  $\beta_z$ (as labelled).
$\beta_z$ (as labelled).
As mentioned earlier, the presence of magnetic resistivity can lead to a thicker disc. According to Equation (26), the infall velocity is expected to increase due to an enhancement of the magnetic resistivity. Our results indicate that the radial velocity rises significantly in about  $P_m=0.5$. At the higher magnetic Prandtl number, however, the infall velocity of the disc material remains almost unchanged. Although the outflows in this limit cannot significantly affect the radial velocity, the role of outflows in the modification of angular velocity is very important (see also Mosallanezhad et al. Reference Mosallanezhad, Khajavi and Abbassi2013). The reason is as follows. In this paper, the outflows are assumed to extract the angular momentum. The angular momentum extracted from the disc enhances the angular velocity. We find that the rotational velocity depends not only on the wind strength but also on the magnetic Prandtl number. A decrease in the magnetic Prandtl number causes the disc to rotate with a slower rate. Such a reduction in the rotational velocity could result from the increase of disc thickness with the magnetic resistivity (see Equation (27)). One can see that there is a specific magnetic Prandtl number in which the disc reaches a non-rotating limit. The value of such a specific magnetic Prandtl number depends on the power law index s because the rotational velocity is highly sensitive to the wind strength and the disc thickness. One find when stronger winds exist, the disc tends to a non-rotating limit in smaller
$P_m=0.5$. At the higher magnetic Prandtl number, however, the infall velocity of the disc material remains almost unchanged. Although the outflows in this limit cannot significantly affect the radial velocity, the role of outflows in the modification of angular velocity is very important (see also Mosallanezhad et al. Reference Mosallanezhad, Khajavi and Abbassi2013). The reason is as follows. In this paper, the outflows are assumed to extract the angular momentum. The angular momentum extracted from the disc enhances the angular velocity. We find that the rotational velocity depends not only on the wind strength but also on the magnetic Prandtl number. A decrease in the magnetic Prandtl number causes the disc to rotate with a slower rate. Such a reduction in the rotational velocity could result from the increase of disc thickness with the magnetic resistivity (see Equation (27)). One can see that there is a specific magnetic Prandtl number in which the disc reaches a non-rotating limit. The value of such a specific magnetic Prandtl number depends on the power law index s because the rotational velocity is highly sensitive to the wind strength and the disc thickness. One find when stronger winds exist, the disc tends to a non-rotating limit in smaller  $P_m$. In bottom panel of Figure 1, the sound speed is illustrated. As we mentioned, this speed and therefore the disc temperature depend on the parameters s and
$P_m$. In bottom panel of Figure 1, the sound speed is illustrated. As we mentioned, this speed and therefore the disc temperature depend on the parameters s and  $P_m$. The sound speed can approach the Keplerian speed when
$P_m$. The sound speed can approach the Keplerian speed when  ${P_m}^{-1}$ exceeds unity. The reduction in disc temperature due to an increase in the value of s and
${P_m}^{-1}$ exceeds unity. The reduction in disc temperature due to an increase in the value of s and  $P_m$ is in good agreement with findings of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012).
$P_m$ is in good agreement with findings of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012).
The influence of  $\beta_{\phi}$ is displayed in Figure 2. In this figure, the power law index s is 0.2, and
$\beta_{\phi}$ is displayed in Figure 2. In this figure, the power law index s is 0.2, and  $\beta_{\phi}$ can vary from 0.01 (i.e.,
$\beta_{\phi}$ can vary from 0.01 (i.e.,  ${c_{\phi}}^2=0.02{c_s}^2$) to 2.0 (i.e.,
${c_{\phi}}^2=0.02{c_s}^2$) to 2.0 (i.e.,  ${c_{\phi}}^2=4{c_s}^2$), as labelled. Other input parameters are similar to Figure 1. In Figure 2, higher values of
${c_{\phi}}^2=4{c_s}^2$), as labelled. Other input parameters are similar to Figure 1. In Figure 2, higher values of  $\beta_{\phi}$ are not considered because the ratio
$\beta_{\phi}$ are not considered because the ratio  $H/r$ exceeds unity (see top left panel of Figure 2). The dependence of the magnetic heating on the azimuthal field component implies that the stronger fields enhance the magnetic heating and the gas temperature. With increasing the temperature (or the sound speed) due to the toroidal component of the magnetic field; therefore, the disc becomes thicker. These results are in good agreement with previous works (see Reference Ghoreyshi and ShadmehriGhoreyshi & Shadmehri 2020). We find that at
$H/r$ exceeds unity (see top left panel of Figure 2). The dependence of the magnetic heating on the azimuthal field component implies that the stronger fields enhance the magnetic heating and the gas temperature. With increasing the temperature (or the sound speed) due to the toroidal component of the magnetic field; therefore, the disc becomes thicker. These results are in good agreement with previous works (see Reference Ghoreyshi and ShadmehriGhoreyshi & Shadmehri 2020). We find that at  $P_m=10$, e.g. the enhancement of
$P_m=10$, e.g. the enhancement of  $\beta_{\phi}$ from 0.1 to 2.0 causes the ratio
$\beta_{\phi}$ from 0.1 to 2.0 causes the ratio  $H/r$ to rise by two orders of magnitude. When the vertical field component is ignored, our results would be similar to findings of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012). Our results indicate that a stronger toroidal component can enhance the infall and the rotational velocities. A combination of Equations (26) and (28) exhibits that the radial velocity is proportional to
$H/r$ to rise by two orders of magnitude. When the vertical field component is ignored, our results would be similar to findings of Faghei & Mollatayefeh (Reference Faghei and Mollatayefeh2012). Our results indicate that a stronger toroidal component can enhance the infall and the rotational velocities. A combination of Equations (26) and (28) exhibits that the radial velocity is proportional to  $\sqrt{1+\beta_{\phi}}C_3$. Thus, the material can move radially inward with faster rate when a stronger azimuthal field component is considered. In order to explore the role of toroidal field component in the rotational velocity, it is helpful to compare the second term with the third one in Equation (27). For our input parameters, the value of the second term, i.e. the gradient of the total pressure plus the magnetic stress force, rises with increasing
$\sqrt{1+\beta_{\phi}}C_3$. Thus, the material can move radially inward with faster rate when a stronger azimuthal field component is considered. In order to explore the role of toroidal field component in the rotational velocity, it is helpful to compare the second term with the third one in Equation (27). For our input parameters, the value of the second term, i.e. the gradient of the total pressure plus the magnetic stress force, rises with increasing  $\beta_{\phi}$. But the third term reduces as
$\beta_{\phi}$. But the third term reduces as  $\beta_{\phi}$ increases. Since the value of third term is smaller than the value of second one, the rotational velocity rises for stronger magnetic field. The previous studies of a resistive ADAF also showed that the toroidal component of the magnetic field can increase these velocities (Faghei & Mollatayefeh Reference Faghei and Mollatayefeh2012). Note that the specific magnetic Prandtl number in which the disc has a non-rotating motion is almost independent of the input parameter
$\beta_{\phi}$ increases. Since the value of third term is smaller than the value of second one, the rotational velocity rises for stronger magnetic field. The previous studies of a resistive ADAF also showed that the toroidal component of the magnetic field can increase these velocities (Faghei & Mollatayefeh Reference Faghei and Mollatayefeh2012). Note that the specific magnetic Prandtl number in which the disc has a non-rotating motion is almost independent of the input parameter  $\beta_{\phi}$. A comparison between Figures 1 and 2 shows that the role of wind in the changes of velocities is more important. One can expect that an increase in
$\beta_{\phi}$. A comparison between Figures 1 and 2 shows that the role of wind in the changes of velocities is more important. One can expect that an increase in  $\beta_{\phi}$ leads to a reduction in the surface density which can be because of the increase of radial velocity (see Equation (19)). Even if the radial field component is considered, the surface density decreases with increasing
$\beta_{\phi}$ leads to a reduction in the surface density which can be because of the increase of radial velocity (see Equation (19)). Even if the radial field component is considered, the surface density decreases with increasing  $\beta_{\phi}$ (see Mosallanezhad et al. Reference Mosallanezhad, Khajavi and Abbassi2013).
$\beta_{\phi}$ (see Mosallanezhad et al. Reference Mosallanezhad, Khajavi and Abbassi2013).
Figure 3 displays the obtained results of investigation of the role of  $\beta_z$ when
$\beta_z$ when  $s=0.2$. Here, parameter
$s=0.2$. Here, parameter  $\beta_z$ lies between 0.01 and 2.0, as labelled, and other parameters are similar to Figure 1. Under these condition, we find that the effect of vertical field component on almost all variables depends on the magnetic Prandtl number. It results from the dependence of magnetic heating on the vertical field component. A comparison between the two terms of the magnetic heating exhibits that the coefficient related to the vertical field component is greater than that related to the toroidal component of the magnetic field. Thus, the influence of vertical field component can be more significant. In Figure 3, one can see that the behaviour of disc variables for different values of
$\beta_z$ lies between 0.01 and 2.0, as labelled, and other parameters are similar to Figure 1. Under these condition, we find that the effect of vertical field component on almost all variables depends on the magnetic Prandtl number. It results from the dependence of magnetic heating on the vertical field component. A comparison between the two terms of the magnetic heating exhibits that the coefficient related to the vertical field component is greater than that related to the toroidal component of the magnetic field. Thus, the influence of vertical field component can be more significant. In Figure 3, one can see that the behaviour of disc variables for different values of  $\beta_z$ changes at a specific magnetic Prandtl number about
$\beta_z$ changes at a specific magnetic Prandtl number about  ${P_m}^{-1}=1.1$. When
${P_m}^{-1}=1.1$. When  ${P_m}^{-1}<1.1$, e.g. the ratio
${P_m}^{-1}<1.1$, e.g. the ratio  $H/r$ drops as the input parameter
$H/r$ drops as the input parameter  $\beta_z$ rises. But this trend would be reversed if
$\beta_z$ rises. But this trend would be reversed if  ${P_m}^{-1}>1.1$. Since the rotational velocity is highly sensitive to the vertical field component (Equation (27)), this velocity among the variables examined in this paper does not obey this trend. For our input parameters, the sign of the second term in Equation (27) is negative, and an increase in
${P_m}^{-1}>1.1$. Since the rotational velocity is highly sensitive to the vertical field component (Equation (27)), this velocity among the variables examined in this paper does not obey this trend. For our input parameters, the sign of the second term in Equation (27) is negative, and an increase in  $\beta_z$ results in a greater absolute value for this term. Hence, a larger
$\beta_z$ results in a greater absolute value for this term. Hence, a larger  $\beta_z$, unlike
$\beta_z$, unlike  $\beta_{\phi}$, causes the disc material to rotate with a slower rate (see also Cao & Spruit Reference Cao and Spruit2013; Cao Reference Cao2014). Mosallanezhad et al. (Reference Mosallanezhad, Khajavi and Abbassi2013) also showed that there is a such trend for the rotational velocity in the absence of ohmic dissipation. For adopted range of
$\beta_{\phi}$, causes the disc material to rotate with a slower rate (see also Cao & Spruit Reference Cao and Spruit2013; Cao Reference Cao2014). Mosallanezhad et al. (Reference Mosallanezhad, Khajavi and Abbassi2013) also showed that there is a such trend for the rotational velocity in the absence of ohmic dissipation. For adopted range of  $P_m$, the disc reaches a non-rotating limit when the vertical component of the magnetic field is strong enough. We also examine the effect of wind strength on
$P_m$, the disc reaches a non-rotating limit when the vertical component of the magnetic field is strong enough. We also examine the effect of wind strength on  $\Omega(P_m)$. Our results indicate that the power law index s plays no role in vanishing the rotational velocity if the vertical component of the field is absent. This means that
$\Omega(P_m)$. Our results indicate that the power law index s plays no role in vanishing the rotational velocity if the vertical component of the field is absent. This means that  $\Omega(P_m)$ only due to the presence of strong vertical field falls to zero (compare all plots of
$\Omega(P_m)$ only due to the presence of strong vertical field falls to zero (compare all plots of  $\Omega(P_m)$ in our model). Although the outflow is not the agent of vanishing
$\Omega(P_m)$ in our model). Although the outflow is not the agent of vanishing  $\Omega(P_m)$, its strength can affect the magnitude of the magnetic Prandtl number
$\Omega(P_m)$, its strength can affect the magnitude of the magnetic Prandtl number  $P_m$ in which the non-rotating limit occurs.
$P_m$ in which the non-rotating limit occurs.
As the next step towards a more complete description of resistive discs, we explore the role  $\alpha$ in the disc properties (see Figure 4). According to Equation (11), we expect that the parameter
$\alpha$ in the disc properties (see Figure 4). According to Equation (11), we expect that the parameter $\alpha$ affects significantly the magnetic Prandtl number and therefore the disc variables. In Figure 4, the parameter
$\alpha$ affects significantly the magnetic Prandtl number and therefore the disc variables. In Figure 4, the parameter  $\alpha$ is assumed to vary from 0.1 to 1.0. We studied the influence of smaller values of
$\alpha$ is assumed to vary from 0.1 to 1.0. We studied the influence of smaller values of  $\alpha$, e.g. 0.01, and found that the difference between
$\alpha$, e.g. 0.01, and found that the difference between  $\alpha=0.01$ and 0.1 is not important (see also Beckert Reference Beckert2000). Except the radial velocity, increasing the viscosity parameter
$\alpha=0.01$ and 0.1 is not important (see also Beckert Reference Beckert2000). Except the radial velocity, increasing the viscosity parameter  $\alpha$ can reduce the variables examined in this work. We obtain the ratio of total heating rate to cooling rate as a function of
$\alpha$ can reduce the variables examined in this work. We obtain the ratio of total heating rate to cooling rate as a function of  $P_m$ and of
$P_m$ and of  $\alpha$. The cooling rate dominates the total heating rate if this ratio is below unity. As seen in previous figures, this ratio is greater than 1 and increases as the magnetic resistivity becomes more important. Furthermore, this ratio falls as the viscosity parameter grows. Hence, the temperature and the thickness of disc decrease with increasing
$\alpha$. The cooling rate dominates the total heating rate if this ratio is below unity. As seen in previous figures, this ratio is greater than 1 and increases as the magnetic resistivity becomes more important. Furthermore, this ratio falls as the viscosity parameter grows. Hence, the temperature and the thickness of disc decrease with increasing  $\alpha$. Although the infall velocity is related to
$\alpha$. Although the infall velocity is related to  ${(H/r)}^2$, it is also proportional to the viscosity parameter (see Equation (26)). Thus, an increase in the viscosity parameter enhances the radial velocity. Indeed, the discs with higher viscosity parameter are able to transport higher angular momentum, and therefore the disc material moves inward with faster rate. Subsequently, the increase of infall velocity leads to a lower surface density (see Equation (19)). For small values of the magnetic Prandtl number, the decrease of surface density due to the viscosity parameter is not significant. But if the viscosity parameter increases from 0.1 to 1.0, the surface density falls by ten orders of magnitude at high-magnetic Prandtl number limit. In such a limit of
${(H/r)}^2$, it is also proportional to the viscosity parameter (see Equation (26)). Thus, an increase in the viscosity parameter enhances the radial velocity. Indeed, the discs with higher viscosity parameter are able to transport higher angular momentum, and therefore the disc material moves inward with faster rate. Subsequently, the increase of infall velocity leads to a lower surface density (see Equation (19)). For small values of the magnetic Prandtl number, the decrease of surface density due to the viscosity parameter is not significant. But if the viscosity parameter increases from 0.1 to 1.0, the surface density falls by ten orders of magnitude at high-magnetic Prandtl number limit. In such a limit of  $P_m$, however, the change in
$P_m$, however, the change in  $\alpha$ from 0.1 to 1.0 causes the infall velocity to increase by seven orders of magnitude. One can also see that the magnetic Prandtl number in which the non-rotating limit occurs is nearly independent of the viscosity parameter.
$\alpha$ from 0.1 to 1.0 causes the infall velocity to increase by seven orders of magnitude. One can also see that the magnetic Prandtl number in which the non-rotating limit occurs is nearly independent of the viscosity parameter.

Figure 4. Similar to Figure 1, but for  $s=0.2$ and different values of
$s=0.2$ and different values of  $\alpha$ (as labelled).
$\alpha$ (as labelled).
5. Summary and discussion
The existence of outflows and large-scale magnetic fields in the inner regions of an ADAF have been confirmed by numerical simulation. In such regions of ADAFs, the magnetic diffusivity can play an important role in determining the properties of ADAFs. In the present paper, therefore, we investigated the dynamics of resistive ADAFs with coexistent outflows and large-scale magnetic fields. The large-scale magnetic fields were assumed to have z and  $\phi$ components. Here, the outflows can extract the mass, the angular momentum, and the energy from the disc. In the presence of outflows, numerical simulations, and observations suggest a power-law function for the accretion rate whose power law index represents the wind strength. We assumed a steady-state flow and presented the self-similar solutions that are described by a function of the radial distance.
$\phi$ components. Here, the outflows can extract the mass, the angular momentum, and the energy from the disc. In the presence of outflows, numerical simulations, and observations suggest a power-law function for the accretion rate whose power law index represents the wind strength. We assumed a steady-state flow and presented the self-similar solutions that are described by a function of the radial distance.
Our self-similar solutions indicated that the rotational velocity of an ADAF threaded by large-scale magnetic field lines is always sub-Keplerian, in good agreement with previous works (see Ogilvie & Livio Reference Ogilvie and Livio1998, Reference Ogilvie and Livio2001; Cao & Spruit Reference Cao and Spruit2002; Cao Reference Cao2012). However, the infall velocity in high-magnetic diffusivity limit can be close to the Keplerian speed. When the magnetic diffusivity becomes stronger, i.e. small- $P_m$ limit, the disc reaches a non-rotating limit and has a purely radial motion. Under such conditions, one can expect that the accretion rate of an ADAF rises. The changing accretion rate can alter the black hole luminosity (Bu & Yang Reference Bu and Yang2019). We also found that the rotational velocity depends strongly on the outflow and the vertical component of field. If the vertical field component is assumed to be weaker, the disc can rotate with a faster rate. When outflow is present, the rotational velocity increases with increasing the outflow strength. As mentioned previously, the infall velocity in small-
$P_m$ limit, the disc reaches a non-rotating limit and has a purely radial motion. Under such conditions, one can expect that the accretion rate of an ADAF rises. The changing accretion rate can alter the black hole luminosity (Bu & Yang Reference Bu and Yang2019). We also found that the rotational velocity depends strongly on the outflow and the vertical component of field. If the vertical field component is assumed to be weaker, the disc can rotate with a faster rate. When outflow is present, the rotational velocity increases with increasing the outflow strength. As mentioned previously, the infall velocity in small- $P_m$ limit increases significantly due to the presence of magnetic diffusivity, so that the radial velocity of the disc material approaches the Keplerian speed. This increase is more significant when both vertical and azimuthal components of the large-scale magnetic field get stronger. Since the discs with higher viscosity parameter are able to transport higher angular momentum, the disc material moves inward with faster rate. This can lead to a high mass accretion rate.
$P_m$ limit increases significantly due to the presence of magnetic diffusivity, so that the radial velocity of the disc material approaches the Keplerian speed. This increase is more significant when both vertical and azimuthal components of the large-scale magnetic field get stronger. Since the discs with higher viscosity parameter are able to transport higher angular momentum, the disc material moves inward with faster rate. This can lead to a high mass accretion rate.
We found that the surface density generally tends to zero in the high-magnetic diffusivity limit, unless the vertical field component is weak. Since the infall velocity, and therefore accretion rate increases at this limit, the surface density of a resistivity disc decreases significantly. Any change in the density profile can affect the emitted spectrum of an accretion flow. Although the surface density decreases with the increase of azimuthal field component, the effect of vertical field component on the surface density depends on the magnetic diffusivity. In large-magnetic diffusivity limit, the role of vertical field component in the modification of density profile is similar to what we found for the azimuthal field component. In the opposite limit, however, the trend of vertical field component will be different.
Our results showed that the disc becomes thicker with increasing the magnetic diffusivity. The disc thickness decreases as the wind strength or the viscosity parameter increases, while the disc becomes thicker for stronger azimuthal field component. We also displayed that an increase in the wind strength (or the viscosity parameter) reduces the disc temperature, while stronger azimuthal field component enhances the temperature. The temperature of an ADAF decreases due to stronger vertical field component only if small-magnetic diffusivity limit is considered. Indeed, the role of vertical field component in decreasing the disc temperature depends on the magnetic diffusivity. A comparison between our results and previous works shows that the effective agent of temperature reduction is outflows and the decreases of temperature due to the vertical field component are seen only in ideal MHD and/or non-ideal MHD with low resistivity.
Although the self-similar solutions presented in this work may be very simplified, these solutions help us to understand the physics of ADAFs around a black hole and the origin of some observational phenomena. One example is the strong variations in the infrared and X-ray bands of Sgr A*. These fluctuations referred to as flares occur almost every day (e.g. Hornstein et al. Reference Hornstein, Matthews, Ghez, Lu, Morris, Becklin, Rafelski and Baganoff2007; Dodds-Eden et al. Reference Dodds-Eden2009). The origin of the flares may be the electrons that are heated to higher temperatures and accelerated into a relativistic power-law distribution. The heating and the acceleration of the electrons in hot accretion flows could result from the magnetic reconnection (Dodds-Eden et al. Reference Dodds-Eden2009; Ding et al. Reference Ding, Yuan and Liang2010). Takahashi & Ohsuga (Reference Takahashi and Ohsuga2013) showed that the enhancement of the resistivity causes the magnetic field lines to start to reconnect. Hence, the presence of the resistivity can lead to the heating and the acceleration of electrons. Furthermore, Ding et al. (Reference Ding, Yuan and Liang2010) suggested that the resistive heating may be helpful to heat the electrons to higher temperatures, as we found in this work.
Acknowledgements
The author would like to thank an unknown referee for a constructive report. The author thanks Dr. Mohsen Shadmehri for a helpful comment.















