1 INTRODUCTION
As a by-product of the sky surveys made by the GALEX satellite (Morrissey et al. Reference Morrissey2007), measurements of far-ultraviolet (FUV) brightnesses were made for large numbers of stars in the solar neighbourhood. Of interest in this paper are late-type dwarf stars of spectral types F, G and K. Such stars engage in chromospheric and coronal activity. The FUV wavelength range contains not only emission lines from the chromosphere and transition region (e.g., Ayres, Marstad, & Linsky Reference Ayres, Marstad and Linsky1981), but also continuum flux from the chromosphere (Vernazza, Avrett, & Loeser Reference Vernazza, Avrett and Loeser1981; Linsky et al. Reference Linsky, Bushinsky, Ayres, Fontenla and France2012). Loyd et al. (Reference Loyd2016) have, for example, used HST COS spectra to detect chromospheric continuum emission within the GALEX FUV wavelength range for the bright star ε Eri (K2V) and possibly HD 97658 (K1V). The relationship between FUV flux and chromospheric activity as manifested in the emission cores of the Ca
${\rm \scriptstyle II}$
H and K lines has been discussed by Smith & Redenbaugh (Reference Smith and Redenbaugh2010; SR10) and Findeisen, Hillenbrand, & Soderblom (Reference Findeisen, Hillenbrand and Soderblom2011), both of whom found clear correlations for stars later than mid-F spectral type.
Among late-type dwarfs, stellar activity also governs the properties of the corona. Correlations between Ca
${\rm \scriptstyle II}$
H and K emission and coronal soft X-ray emission have been documented in the literature (e.g., Hempelmann, Schmitt, & Stepien Reference Hempelmann, Schmitt and Stepien1996; Mamajek & Hillenbrand Reference Mamajek and Hillenbrand2008; Smith & Sheretz Reference Smith and Sherertz2012), as have correlations between luminosity in soft X-rays and various other emission lines originating from the chromosphere and transition region (e.g., Ayres et al. Reference Ayres, Marstad and Linsky1981, Reference Ayres, Simon, Stauffer, Stern, Pye and Brown1996; Güdel Reference Güdel2004). Thus, it would follow that GALEX FUV magnitudes of late-type dwarfs should show a relation with soft X-ray emission. A catalogue of homogeneous measurements of X-ray luminosities of dwarf stars published by Hünsch, Schmitt, & Voges (Reference Hünsch, Schmitt and Voges1998; HSV98) from ROSAT data provides a well-suited data base with which to test this expectation.
The present study complements and provides contrast with SR10 in several ways.
-
(i) It compares FUV brightnesses of late-type dwarfs measured by GALEX with a coronal activity indicator rather than a chromospheric indicator. Comparisons are made between the FUV brightness excess and both absolute (L x) and normalized (L x/L bol) soft X-ray luminosities.
-
(ii) The utility of the chromospheric Ca
${\rm \scriptstyle II}$
H and K emission lines used by SR10 is largely restricted to dwarfs later than F2–F5, i.e., (B − V) > 0.35–0.45 or (b − y) > 0.22–0.28 (Wilson Reference Wilson1968; Linsky et al. Reference Linsky, McClintock, Robertson and Worden1979; Dravins Reference Dravins1981), and the hottest dwarfs in the SR10 sample have B − V ~ 0.42. By contrast the HSV98 ROSAT sample of dwarfs extends to A stars, and is more weighted to F dwarfs than the SR10 study. -
(iii) SR10 used FUV magnitudes from the GALEX GR3/4 data release. In this paper data are taken from the more extensive and refined GR6/7 release.
-
(iv) The coronal soft X-ray dataset used here is from a more homogeneous source (the ROSAT satellite) than the multiple literature sources of log R′HK compiled by SR10.
2 DATA COMPILATION
The starting point for this work was the sample of main sequence stars for which Hünsch et al. (Reference Hünsch, Schmitt and Voges1998; HSV98) derived soft X-ray luminosities L x in erg s−1 from measurements made by the ROSAT satellite. For consistency with their study we have adopted the same Johnson V and B − V photometry and Hipparcos (Perryman et al. Reference Perryman1997) parallax-based distances used by HSV98, together with bolometric corrections from Flower (Reference Flower1996), to calculate X-ray luminosities L x/L bol normalised to the stellar bolometric luminosity. Stars for which (B − V) ⩾ 0.30 from HSV98 were searched for in the GALEX General Data Release version 6/7, and values of the FUV magnitude m FUV were compiled. Information on binarity for stars in the resulting GALEX-HSV98 overlap sample was taken from the paper of HSV98 itself, wherein stars are designated as single, visual binaries, or spectroscopic binaries, together with comparable information gleaned from the SIMBAD Astronomical Database (Wenger et al. Reference Wenger2000), which also identifies certain types of variables such as W UMa and BY Dra stars. Several components of binary stars in HSV98 were removed from consideration because of ambiguity in the X-ray fluxes. In all, 309 stars constitute the GALEX-HSV98 overlap sample that is used below.
The GALEX Catalog Search toolFootnote 1 was used to search for FUV detections around each HSV98 star. The search radius was set to 0.2 arcmin, with SIMBAD used as the Resolver service to look up sky coordinates for each object name. Successful searches returned one or more lines of magnitude data per object name. In lines labelled ‘band 3’ both FUV and NUV magnitudes were returned, in other lines labelled ‘band 2’ only a FUV magnitude was given. Multiple band 3 listings were averaged, as were multiple band 2 listings, and recorded separately. Band 3 and band 2 m FUV values were then combined with equal weight. Based on 38 stars from HSV98 for which listings were returned in both bands by the Search tool, the mean value of the difference m FUV(band 3) − m FUV(band 2) is 0.04 mag with a standard deviation of 0.12 mag. On this basis a 1σ uncertainty in the FUV magnitudes for the GALEX-HSV98 sample is taken to be 0.12 mag. This can be compared with a photometric repeatability of 0.05 mag in m FUV quoted by Morrissey et al. (Reference Morrissey2007).
3 LATE-F, G AND EARLY-K DWARFS
A plot of (m FUV − B) versus (B − V) for the GALEX-HSV98 overlap sample is shown in Figure 1. It is morphologically similar to Figure 3 of Smith & Redenbaugh (Reference Smith and Redenbaugh2010), which is based on GR3/4 photometry for a different sample of dwarfs, and not as well populated by F stars with (B − V) < 0.4. Among dwarfs with 0.3 ⩽ (B − V) ⩽ 0.8 there is a clear trend in (m FUV − B) with B − V that is driven by a change in the photospheric FUV spectrum with effective temperature. Superimposed on this trend is a scatter in (m FUV − B) that exceeds the 3σ ~ 0.4 mag observational uncertainties, and as shown below is related to stellar activity. The symbols used in Figure 1 are encoded according to stellar binarity, as discussed in the caption. Stars are denoted as ‘suspected’ visual or spectroscopic binaries if they are listed as such a binary in one but not both of the sources HSV98 and SIMBAD.
Figure 1. The FUV-based colour (m FUV − B) versus (B − V) for dwarf stars in the GALEX (HSV98-ROSAT) overlap sample. The solid line corresponds to equations (1) and (2) and forms an upper envelope to the distribution of stars with respect to which an FUV-excess denoted Δ(m FUV − B) is measured. Symbols in the plot refer to different categories of stars: (filled circles) single stars; (filled hexagon) visual binaries; (open hexagon) suspected visual binaries; (filled triangle) spectroscopic binaries; (open triangle) suspected spectroscopic binaries; (four-sided star) RS CVn variables; (three-sided star) BY Dra variables. The dashed line shows a locus for purely photospheric emission as given by the models of Findeisen et al. (Reference Findeisen, Hillenbrand and Soderblom2011).
Most of the GALEX-HSV98 stars with (B − V) ⩽ 0.80 fall below a fiducial locus which is shown in Figure 1 as a solid line. The plotted fiducial, which was chosen by eye to serve as an upper envelope to the data points for (B − V) ⩽ 0.80, has been divided into two sections having the equations
$$\begin{equation}
(m_{\rm FUV} - B)_{\rm F} = 16.00(B-V) + 2.60
\end{equation}$$
for 0.30 ⩽ B − V ⩽ 0.50, and
$$\begin{equation}
(m_{\rm FUV} - B)_{\rm F} = 8.667(B-V) + 6.27
\end{equation}$$
for 0.50 ⩽ B − V ⩽ 0.80. The fiducial locus is likely to be set by dwarfs with the lowest levels of stellar activity at a given (B − V) colour. As emission from stellar activity increases at FUV wavelengths, the (m FUV − B) colour would become bluer for a fixed effective temperature. The scatter of stars below the fiducial in Figure 1 increases towards redder (B − V), indicative of an increase in contrast between the chromospheric/transition-region and photospheric contributions to the FUV flux.
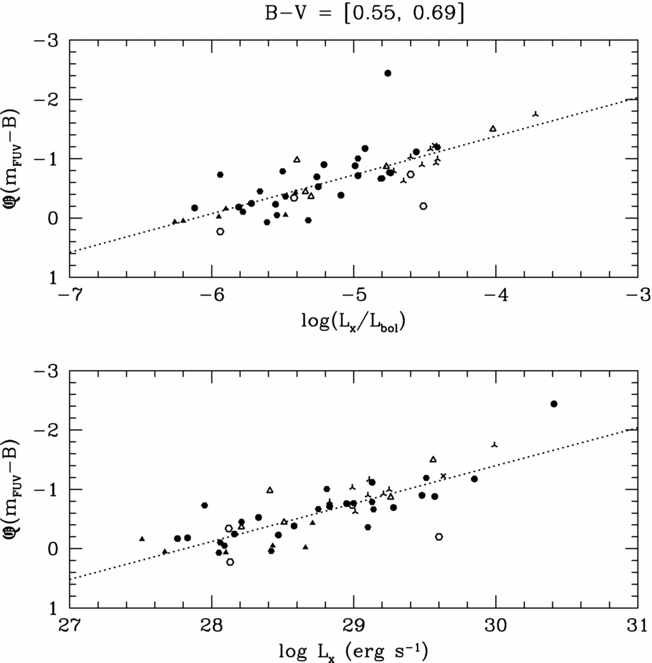
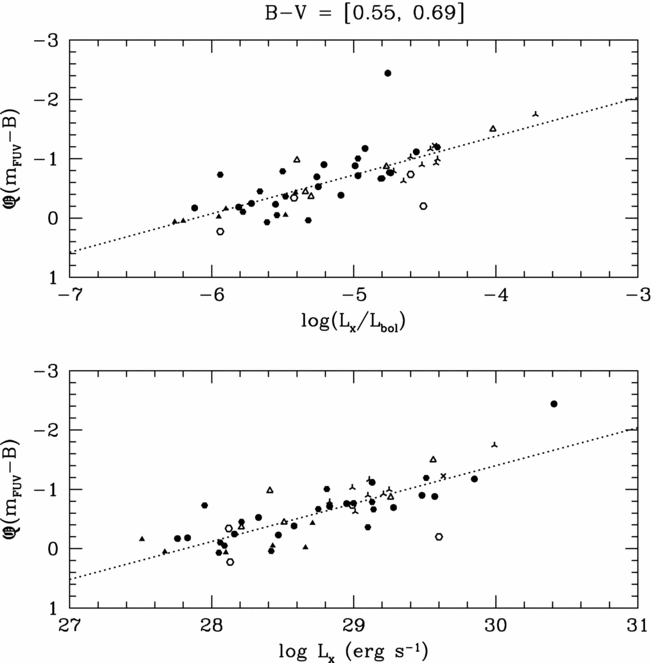
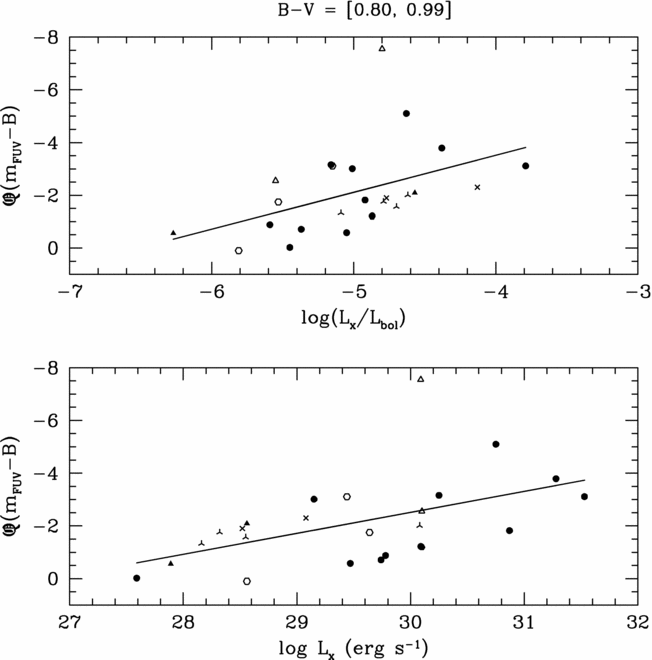
An FUV excess defined as Q(m FUV − B) = (m FUV − B)star − (m FUV − B)F measures the vertical displacement in Figure 1 of a star from the location of the fiducial upper envelope. A measurable enhancement in stellar activity at a given (B − V) would cause the Q(m FUV − B) excess to become more negative by virtue of an increasing flux in the FUV bandpass relative to the B band. Plots of Q(m FUV − B) versus both L x and log (L x/L bol) are shown in Figures 2–5 for dwarfs binned into various (B − V) colour intervals. Symbols again denote stellar binarity in the same manner as in Figure 1. Correlations are discernible for dwarfs redder than (B − V) ⩾ 0.50. The X-ray luminosities of most stars depicted in Figures 2–5 fall below the saturation regime of −3.3 ⩽ log (L x/L bol) ⩽ −3.0 found by Vilhu & Walter (Reference Vilhu and Walter1987) for coronal activity (see also, for example, Güdel Reference Güdel2004).
Figure 3. The photometric parameter Q(m FUV − B) versus both log (L x/L bol) (top) and log L x (bottom) for dwarfs in the colour range 0.50 ⩽ (B − V) ⩽ 0.54. The solid line is a least-squares fit to each dataset, the coefficients of which are given in Table 1. The dashed line is a corresponding fit shown in Figure 2 for dwarfs in the colour range 0.55 ⩽ (B − V) ⩽ 0.69. Symbols are the same as for Figure 1.
Figure 4. The photometric parameter Q(m FUV − B) versus log L x (bottom) and log (L x/L bol) (top) for dwarfs in the colour range 0.70 ⩽ (B − V) ⩽ 0.79. The solid line is a least-squares fit to each dataset, the coefficients of which are given in Table 1. The dashed line is a corresponding fit shown in Figure 2 for dwarfs in the colour range 0.55 ⩽ (B − V) ⩽ 0.69. Symbols are the same as for Figure 1.
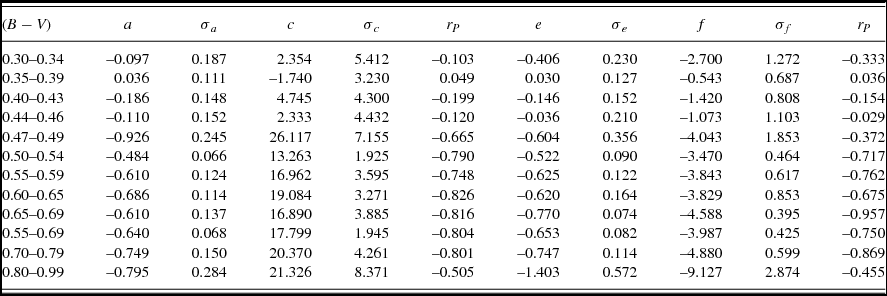
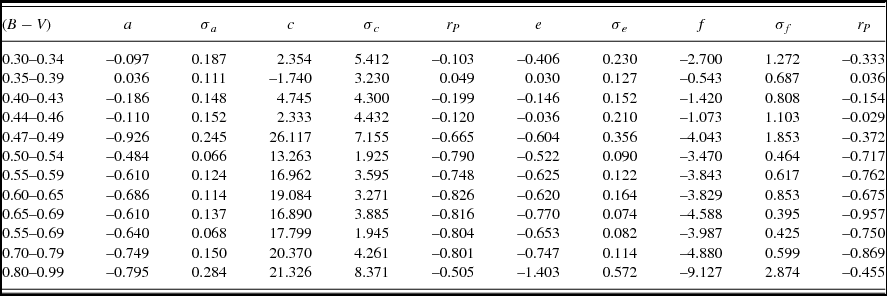
Statistical tests for correlations between FUV and soft X-ray emission among dwarfs in various ranges of (B − V) colour were made through use of the lsq and rxy macros within the Supermongo plotting package (Lupton & Monger Reference Lupton and Monger1997). The former macro has been used to make least-squares linear fits to the data of the form
$$\begin{equation}
Q(m_{\rm FUV}-B) = a \log L_{\rm x} + c
\end{equation}$$
and
$$\begin{equation}
Q(m_{\rm FUV}-B) = e \log (L_{\rm x}/L_{\rm bol}) + f.
\end{equation}$$
Table 1 gives values of the coefficients a, c, e and f in these fits for the different B − V colour ranges, together with the standard deviations, and value of the Pearson correlation coefficient r P (obtained from the rxy macro). After making initial fits, several stars with Q(m FUV − B) < −3.0 mag or >+1.0 mag were removed from consideration in obtaining the results of Table 1, since their data points fell well away from both the initial and final regression lines. Otherwise, all stars regardless of binarity were used in obtaining the fits summarised in Table 1 (which in Figures 3–5 are shown by solid lines). The Pearson coefficients for the dwarf groupings with (B − V) ⩾ 0.50 are strongly indicative of correlations between Q(m FUV − B) and both measures of soft X-ray luminosity. By comparison, the values of r P for all groups of stars with (B − V) < 0.47 give little to no evidence of correlations.
The fits for stars in the three (B − V) colour groups of 0.55–0.59, 0.60–0.65, and 0.65–0.69 mag are found to be very similar (Table 1). On this basis, in an attempt to obtain a fit appropriate for dwarfs of solar-like effective temperature that has reduced formal uncertainties, fits were also made to stars in the wider 0.55–0.69 mag colour range. The results are given in Table 1 and shown in Figure 2 as dashed lines. These lines are also shown for reference in Figures 3 and 4.
Stars within the (B − V) colour bins 0.50–0.54 (Figure 3) and 0.70–0.79 (Figure 4) exhibit correlations between Q(m FUV − B) and both measures of X-ray luminosity. For the redder dwarfs in Figure 4 there is an offset between the best fits and those for solar-like stars, although the slopes do not much differ. The redder sample of dwarfs in Figure 4 is of modest size, and the stars with highest X-ray luminosity in this group are binary systems, particularly W UMa and BY Dra variables.
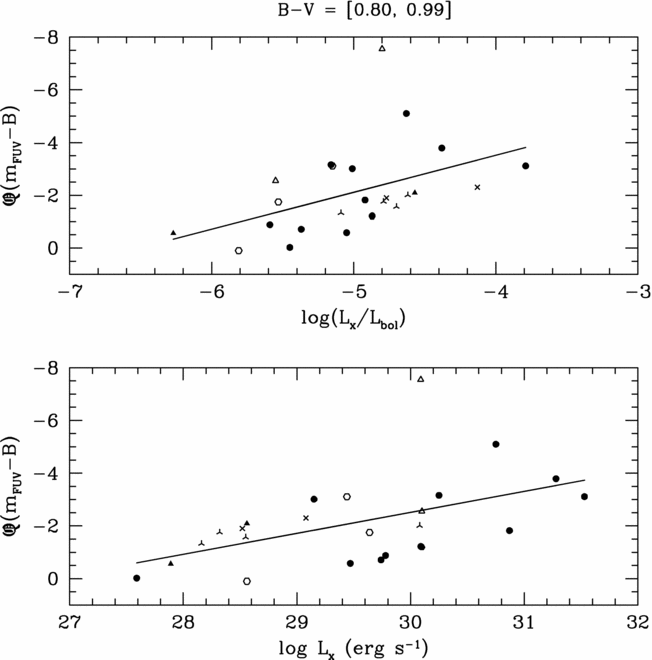
Among dwarfs redder than 0.80 mag in (B − V), there is no well-defined upper envelope to the data points in Figure 1. In particular, equation (2) would not appear to be relevant at such red colours. Consequently (m FUV − B)F = 13.20 was adopted for such stars, this being the value corresponding to equation (2) at B − V = 0.80 mag. The resulting values of Q(m FUV − B) for dwarfs with 0.80 ⩽ (B − V) ⩽ 0.99 are plotted versus soft X-ray luminosity in Figure 5. While there are trends, the Pearson correlation coefficient is less strong than for stars throughout the colour range 0.50 ⩽ (B − V) ⩽ 0.80. Separate fits were run for the more restricted colour groupings of 0.80–0.89 and 0.90–0.99, yielding Pearson correlation coefficients in the range −0.41 < r P < −0.61; however, the least-squares fits themselves were more uncertain than those listed in Table 1 for the larger sample within (B − V) = 0.80–0.99. Stars in the GALEX-HSV98 sample with (B − V) > 0.80 mag therefore show weaker correlations between FUV excess and soft X-ray luminosity than dwarfs of more solar-like temperatures.
Residuals were calculated about the least-squares fit equation (3) for dwarfs with 0.55 ⩽ (B − V) ⩽ 0.69, i.e., the data points in the bottom panel of Figure 2. These residuals are denoted as δ ac 5569 Q(m FUV − B). There are 14 non-binary stars in this subset, which have a mean value for δ ac 5569 Q(m FUV − B) of −0.035 (standard deviation 0.274 mag). There are 11 stars classified as spectroscopic or suspected spectroscopic binaries in Figure 2, for which the mean residual is 0.00 (standard deviation 0.33). In the case of the 17 visual binaries (including suspected VBs) the mean residual is 0.094 (standard deviation 0.361). These statistics provide little indication for offsets between the various classes of binarity in Figure 2.
The residual
$\delta ^{\text{ac}}_{5569}Q(m_{\rm FUV}-B)$
is plotted in Figure 6 versus absolute magnitude and soft X-ray hardness ratio HR (from HSV98). There is no correlation with HR, but there is a tendency for δac to be positive for all but one star brighter than M
V
= +3.0. There are 8 stars in Figure 6 with +1.5 < M
V
< +3.0, and they evince a mean δac-residual of 0.27 mag (standard deviation 0.16 mag). Thus dwarfs with solar-like effective temperature that are ⪆2 mag above the zero-age main sequence may be characterised by a slightly off-set relation between Q(m
FUV − B) and L
x. Consequently, if Q(m
FUV − B) were to be used to infer the soft X-ray luminosity of dwarfs with near-solar temperature, extra consideration would be needed for stars that are more than ~2 mag removed from the zero-age main sequence. An additional source of scatter in the correlations of Figures 2–5 may be intrinsic variability in the FUV and/or X-ray luminosities, the GALEX and ROSAT data not being obtained at the same time.
Figure 6. Residuals about equation (3) for dwarfs with 0.55 ⩽ (B − V) ⩽ 0.69 (see Figure 2), denoted as δ ac 5569 Q(m FUV − B), versus absolute magnitude and soft X-ray hardness ratio HR. Symbol key as for Figure 1, namely: (filled circles) single stars; (filled hexagon) visual binaries; (open hexagon) suspected visual binaries; (filled triangle) spectroscopic binaries; (open triangle) suspected spectroscopic binaries; (four-sided star) RS CVn variables; (three-sided star) BY Dra variables.
When considering stars throughout the colour range of (B − V) = 0.55–0.69, the Pearson coefficient depends little on whether Q(m FUV − B) is correlated against log L x or log (L x/L bol). In the literature, both measures of coronal activity have been employed, e.g., Pallavicini et al. (Reference Pallavicini, Golub, Rosner, Vaiana, Ayres and Linsky1981) and Piters et al. (Reference Piters, Schrijver, Schmitt, Rosso, Baliunas, van Paradijs and Zwaan1997) for log L x, and Ayres et al. (Reference Ayres, Marstad and Linsky1981) and Mamajek & Hillenbrand (Reference Mamajek and Hillenbrand2008) for log (L x/L bol). The Pearson correlation coefficients in Table 1 give no consistent picture as to which correlates more tightly with Q(m FUV − B).Footnote 2
4 EARLY-F DWARFS
4.1. Correcting for photospheric FUV emission
The Q-parameter introduced in Section 3 was defined in large part for convenience. A question arises as to the nature of stars that fall on, or close to, the fiducial sequence defined by equations (1) and (2). Is the FUV brightness of such stars entirely photospheric in origin, or is it due to a combination of emission from the photosphere, chromosphere, and transition region?
Absolute magnitudes in a variety of bandpasses, including the GALEX FUV, have been calculated for model photospheres by Findeisen et al. (Reference Findeisen, Hillenbrand and Soderblom2011) for a range of effective temperatures along the main sequence. A photosphere-only locus from their work is plotted in Figure 1 as a dashed line. In the (B − V) range of 0.3–0.4 mag, the model photosphere locus falls close to the fiducial line that we have adopted (equation 1), while the two lines start to diverge mildy in the range 0.4–0.5 mag. Among dwarfs with (B − V) > 0.5, the photosphere-only locus is significantly fainter in FUV magnitude than the fiducial given by equation (2). The comparison indicates that a stellar photosphere will make a significant contribution to flux in the GALEX FUV band for dwarfs of B − V colour bluer than 0.5 mag. A parameter such as Q(m FUV − B), which makes no allowance for a photospheric contribution to the FUV, would be expected to lose utility for tracing stellar activity among such hot dwarfs.
Many observations have shown that early-F dwarfs do have chromospheres, as seen, for example, via emission lines such as λ1335 C
${\rm \scriptstyle II}$
(Schrijver Reference Schrijver1993; Simon & Landsman Reference Simon and Landsman1991) and λ1549 C
${\rm \scriptstyle IV}$
(Wolff, Boesgaard, & Simon Reference Wolff, Boesgaard and Simon1986). Warner (Reference Warner1968) detected Ca
${\rm \scriptstyle II}$
K2 emission in the spectrum of γ Vir N (F1V), one component of a visual binary. Blanco et al. (Reference Blanco, Bruca, Catalano and Marilli1982) found chromospheric Mg
${\rm \scriptstyle II}$
h and k emission among main sequence stars as early as A7V. As such, FUV emission due to activity is to be expected among early-F dwarfs. In this section, we study the dwarfs with (B − V) < 0.50 in more detail by attempting to correct the observed FUV luminosity of such stars for a photospheric component.
Corrections were made for a photospheric component to the FUV brightness of the GALEX-HSV98 dwarfs across the B − V colour range from 0.30 to 0.50 mag. The approach below was followed. A flux F fuv incident at Earth in the FUV band corresponds to a GALEX AB magnitude of m FUV according to the following equationFootnote 3 :
$$\begin{equation*}
m_{\rm FUV} = 18.82 - 2.5 \log \frac{F_{\rm fuv}}{1.40 \times 10^{-15} {\rm (erg/s)} \phantom{i} {\rm cm}^{-2} {\rm \AA}^{-1}}.
\end{equation*}$$
Taking the GALEX FUV bandpass to have a wavelength range of 442 Å (Morrissey et al. Reference Morrissey2005, Reference Morrissey2007), the total FUV flux arriving at Earth can be calculated as
$$\begin{equation}
F_{\rm fuv} = 6.188 \times 10^{-13} \times 10^{0.4(18.82 - m_{\rm FUV})} {\rm (erg/s)}\phantom{i} {\rm cm}^{-2}.
\end{equation}$$
The distances in parsecs from HSV98 (d pc) were adopted to compute the observed soft X-ray luminosity of each star via
$$\begin{eqnarray}
\log L_{\rm fuv,obs} \phantom{i} {\rm (erg/s)} &=& 25.87 + 2 \log d_{\rm pc} \nonumber\\
&&+\, 0.4( 18.82 - m_{\rm FUV} ).
\end{eqnarray}$$
Photospheric FUV fluxes at the surfaces of the program stars were calculated by using a calibration with effective temperature T eff that is given in Shkolnik et al. (Reference Shkolnik and Barman2014):
$$\begin{equation}
f_{\rm fuv,phot} {\rm (erg/s)} \phantom{i} {\rm cm}^{-2} = 10^{[2.640(T_{\rm eff}/10^3) - 10.6934]}
\end{equation}$$
(see also Shkolnik & Barman Reference Shkolnik and Barman2014). This calibration is based on model stellar atmosphere calculations and for FGK stars is anchored by the models of Findeisen et al. (Reference Findeisen, Hillenbrand and Soderblom2011). Photospheric flux was converted to a net luminosity by multiplying by the stellar surface area A, which for current purposes was written in the form
$$\begin{equation}
A = 4 \pi R_{\odot }^2 (T_{\rm eff,\odot }/T_{\rm eff})^4 (L_{\rm bol}/L_{\rm bol,\odot }).
\end{equation}$$
Adopting L bol, ⊙ = 3.845 × 1033 erg s−1, T eff, ⊙ = 5 772 K, and R ⊙ = 6.957 × 1010 cm, the equation used to calculate a stellar photospheric FUV luminosity is
$$\begin{eqnarray}
\log L_{\rm fuv,phot} {\rm (erg/s)} &=& 4 \log (T_{\rm eff,\odot }/T_{\rm eff}) + \log (L_{\rm bol}) \nonumber\\
&& + 2.640(T_{\rm eff}/10^3) - 21.494.
\end{eqnarray}$$
In the case of the GALEX-HSV98 stars in the colour range 0.30 ⩽ (B − V) ⩽ 0.50, the observed total FUV luminosity was calculated from equation (6) and the photospheric FUV luminosity from equation (9). Effective temperatures were chosen according to the calibration versus B − V derived by Flower (Reference Flower1996). The excess FUV luminosity L fuv, exc = L fuv, obs − L fuv, phot is taken to be the result of emission from a chromosphere and transition region.
The ratio between the computed photospheric FUV luminosity and the observed FUV luminosity is shown in the bottom panel of Figure 7. The solid line is a least-squares fit having the equation log L fuv, phot/L fuv, obs = −5.31( ± 0.26)(B − V) + 1.69( ± 0.11). The predicted photospheric FUV luminosity becomes comparable to observed FUV luminosity for dwarfs of (B − V) < 0.34, corresponding to an effective temperature of 7 014 K according to Flower (Reference Flower1996). For dwarfs with a B − V colour redder than 0.5 mag, stellar activity comes to govern emission in the FUV band, enabling the utility of an index like Q(m FUV − B) for tracing stellar activity among cooler dwarfs.
Figure 7. Behaviour of various contributions to the FUV luminosity of F dwarfs. Symbols are the same as for Figure 1. Bottom panel: the ratio between predicted photospheric and observed (total) luminosity in the FUV band versus (B − V) colour. The solid line is a least-squares fit. Top panel: excess luminosity in the FUV band, log (L fuv, exc/L bol), due to stellar activity versus (B − V) colour.
The behaviour of the excess luminosity in the FUV band due to stellar activity is shown as a plot of log (L
fuv, exc/L
bol) versus (B − V) colour in the upper panel of Figure 7. Among dwarfs bluer than (B − V) = 0.40, i.e., hotter than 6 700 K, the FUV excess as a fraction of L
bol shows no systematic trend with (B − V), but for dwarfs cooler than this, there is evident in Figure 7 a systematic decline in log (L
fuv, exc/L
bol) with decreasing effective temperature. By comparison, data from Simon & Landsman (Reference Simon and Landsman1991) indicate that the normalised C
${\rm \scriptstyle II}$
flux scaled to the stellar bolometric flux for dwarf stars also shows little systematic variation across the colour range 0.25 < (B − V) < 0.50 (albeit with scatter), with a possible slight decline towards redder (B − V) colour.
In the limit where chromospheric emission in the FUV bandpass is a constant fraction of the stellar bolometric luminosity, the FUV chromospheric flux will increase towards hotter F dwarfs, but by a smaller factor than the increase in photospheric emission.Footnote 4 As such, among dwarfs of sufficiently early spectral type any Q(m FUV − B) versus L x relation could be masked by a combination of observational scatter in the FUV magnitude measurements and a reduced contrast between activity-produced emission and photospheric emission at FUV wavelengths.
4.2. Excess FUV emission versus soft X-ray emission
Correlations were sought between excess FUV luminosity due to stellar activity L fuv, exc and soft X-ray luminosity for dwarfs in five different (B − V) colour intervals within the range 0.30 ⩽ (B − V) ⩽ 0.50. Least-squares linear fits were made to the data as
$$\begin{equation}
\log L_{\rm fuv,exc} = b \log L_{\rm x} + d
\end{equation}$$
and
$$\begin{equation}
\log (L_{\rm fuv,exc}/L_{\rm bol}) = h \log (L_{\rm x}/L_{\rm bol}) + j.
\end{equation}$$
Values of the coefficients b, d, h and j together with the Pearson correlation coefficient r P are listed in Table 2. Plots of both log L fuv, exc versus log L x and log (L fuv, exc/L bol) versus log (L x/L bol) are shown in Figures 8–10 for stars in the (B − V) colour ranges of 0.40–0.43, 0.44–0.46 and 0.47–0.50 mag, respectively. Least-squares fits are shown as solid lines. For these three colour ranges a correlation between log L fuv, exc and log L x is indicated, but not so for the luminosities normalised to bolometric. The Pearson correlation coefficient for equation (10) tends to decrease as B − V becomes bluer (Table 2). There is muted evidence at best for any correlation having the form of equation (11).
Figure 8. FUV luminosity originating from stellar activity L fuv, exc versus soft X-ray luminosity for F dwarfs in the colour range 0.40 ⩽ (B − V) ⩽ 0.43. Top panel: both FUV and X-ray luminosities are normalised to the bolometric luminosity. Bottom panel: both luminosities are in units of erg s−1. Each solid line shows a least-squares fit to a dataset, the coefficients of which are given in Table 2. Symbols are the same as for Figure 1.
Figure 9. FUV luminosity originating from stellar activity L fuv, exc versus soft X-ray luminosity for F dwarfs with 0.44 ⩽ (B − V) ⩽ 0.46. Top panel: luminosities are normalised to L bol. Bottom panel: luminosities are in units of erg s−1. Each solid line shows a least-squares fit, the coefficients of which are given in Table 2. Symbols are the same as in Figure 1.
Figure 10. FUV luminosity originating from stellar activity L fuv, exc versus soft X-ray luminosity for F dwarfs with 0.47 ⩽ (B − V) ⩽ 0.50. Top panel: luminosities are normalised to L bol. Bottom panel: luminosities are in units of erg s−1. Each solid line shows a least-squares fit, the coefficients of which are given in Table 2. Symbols are the same as in Figure 1.
Table 2. Least squares fits and Pearson correlation coefficients for equations (10) log L fuv, exc = blog L x + d and (11) log (L fuv, exc/L bol) = hlog (L x/L bol) + j.
On the basis of the Pearson coefficients in Table 2, we conclude that the data reveal a correlation between L fuv, exc and L x for dwarfs in the B − V colour range 0.40–0.50 (corresponding to effective temperatures of 6 725–6 280 K). Among hotter dwarfs, the situation is more ambiguous. As shown in Figure 7, the photospheric FUV luminosity becomes comparable to the total FUV luminosity for dwarfs hotter than 6 700 K, so that for such stars a combination of observational errors in L fuv, obs and uncertainties in L fuv, phot may obscure any intrinsic correlations accompanying stellar activity.
4.3. Early-F dwarfs and evolved G stars
In Section 3 it was shown that among G stars the relation between Q(m FUV − B) and soft X-ray luminosity differs slightly between dwarfs with solar-like absolute magnitude and more evolved G stars that are located more than a magnitude above the main sequence. The stars that appear in Figure 6 at M V ~ 2.0–2.5 and (B − V) = 0.55–0.69 will be more massive than the Sun and evolving through a post-main-sequence phase. For example, a 1.5 M ⊙ star of solar metallicity will evolve through the B − V colour interval from 0.55 to 0.69 mag when the age exceeds ~2.7 Gyr, at which time it will range in absolute magnitude from ~2.3 to 2.7 mag, according to the evolutionary tracks of Lejeune & Schaerer (Reference Lejeune and Schaerer2001). Such a star will commence evolution on the main sequence at M V ~ 3.1 and (B − V) ~ 0.34.Footnote 5 Thus, the progenitors of the evolved G dwarfs in the HSV98 sample will be early-F dwarfs of a higher mass and effective temperature.
Wolff et al. (Reference Wolff, Boesgaard and Simon1986) proposed that stellar activity among early-F dwarfs with shallow convection zones is driven by a different mechanism from the solar-like dynamo which drives activity within late-F and G dwarfs. One option is that the chromospheres of early-F dwarfs are largely maintained by mechanical heating associated with the deposition of energy by acoustic waves, while any dynamo-related heating in such stars is small by comparison (Mullan & Cheng Reference Mullan and Cheng1994; Narain & Ulmschneider Reference Narain and Ulmschneider1996). Stars with M V ~ +2 in Figure 6 will therefore have evolved from early-F dwarfs which spent most of their main sequence phase having chromospheres and coronae of a different physical nature from those of the M V ~ +4-5 dwarfs in the same colour range (B − V = 0.55–0.69). The offset of the brighter stars from the solar-type stars in the Q(m FUV − B) versus L x relation in Figure 2 may, therefore, in part stem from a dissimilarity in the nature of stellar activity among the progenitors of the brighter stars.
5 DISCUSSION
In Section 3, it was shown that it is possible to formulate a fairly straightforward FUV-excess parameter such as Q(m FUV − B) that will correlate with the degree of stellar activity among late-F, G and early K dwarfs. For such stars, it is emission from the chromosphere and transition region that dominates over the photosphere in setting the FUV luminosity.
If we consider two main sequence stars of the same B − V colour and absolute magnitude M V , one on the fiducial locus and one offset from it, the Q(m FUV − B) residual can be written as
$$\begin{equation}
Q(m_{\rm FUV} - B) = -2.5 \log \frac{L_{\rm FUV,p} + L_{\rm FUV,a}}{L_{\rm FUV,p,f} + L_{\rm FUV,a,f}},
\end{equation}$$
where L FUV, p and L FUV, a correspond to the energy per second radiated by a star in the FUV band from the photosphere, and from the chromosphere plus transition region above the photosphere, respectively. The additional subscript f refers to a star on the fiducial locus in Figure 1. By virtue of having identical B − V and M V , the two stars will have the same photospheric FUV luminosity, but can differ in the amount of activity-induced FUV energy loss. In the limit where both L FUV, a ≫ L FUV, p and L FUV, a, f ≫ L FUV, p, f, and if the active region FUV luminosity is related to the soft X-ray luminosity as L FUV, a∝L α x, then
$$\begin{equation}
\alpha \log L_{\rm x} - \alpha \log L_{\rm x,f} = -0.4 Q(m_{\rm FUV} - B),
\end{equation}$$
where L x, f is the X-ray luminosity of the fiducial star. In this case a correlation would be expected between log L x and the FUV excess parameter Q(m FUV − B). This is the situation that was found in Section 3 to pertain to dwarfs in the colour range 0.5 < (B − V) < 1.0, and is consistent with the fact that the fiducial adopted for these stars is well removed from the locus for photospheric emission in Figure 1.
As shown in Section 4, the photospheric and stellar-activity contributions to the FUV luminosity become more comparable among early-F dwarfs than with G and K dwarfs. Additionally, the works of Wolff et al. (Reference Wolff, Boesgaard and Simon1986), Wolff & Heasley (Reference Wolff and Heasley1987) and Walter & Schrijver (Reference Walter, Schrijver, Linsky and Stencel1987) have revealed evidence of a difference in the nature of stellar chromospheres among dwarfs hotter than T
eff = 6 600 K compared to cooler dwarfs. Wolff et al. (Reference Wolff, Boesgaard and Simon1986) found that the onset of stellar activity occurs among F0 dwarfs with B − V ~ 0.28 and T
eff = 7 300 K, i.e., close to the (B − V) lower limit of 0.3 mag that we have adopted for selecting stars from the HSV98 survey (see also Garcia-Lopez et al. Reference Garcia-Lopez, Rebolo, Beckman and McKeith1993; Walter, Matthews, & Linsky Reference Walter, Matthews and Linsky1995; Rachford Reference Rachford1997, Reference Rachford1998). Furthermore, based on a study of the C
${\rm \scriptstyle IV}$
λ1549 and He
${\rm \scriptstyle I}$
λ5876 lines as tracers of stellar activity, Wolff et al. (Reference Wolff, Boesgaard and Simon1986) showed that the characteristics of activity among early-F dwarfs differ from those of late-F dwarfs (see also Simon & Landsman Reference Simon and Landsman1991; Garcia-Lopez et al. Reference Garcia-Lopez, Rebolo, Beckman and McKeith1993; Simon Reference Simon, Lopez, Rebolo and Osorio2001). Among dwarfs hotter than 6 600 K, they found no correlation between the level of stellar activity and stellar rotation, as parameterised by the Rossby number (the ratio between the rotation period of a star and the convective turnover time), whereas cooler F and G dwarfs are characterised by a correlation (see, for example, Noyes et al. Reference Noyes, Hartmann, Baliunas, Duncan and Vaughan1984). Stellar activity as traced by soft X-ray emission evinces an onset of a rotation–activity relation at (B − V) ~ 0.46 (Walter Reference Walter1983; Panzera et al. Reference Panzera, Tagliaferri, Pasinetti and Antonello1999).
Thus, the range in B − V over which a rotation–activity relation has been identified among dwarf stars overlaps that for which a straight-forward parameter such as Q(m FUV − B), which does not take into account subtraction of photospheric flux, can provide a convenient metric of stellar activity (Section 3). For those dwarf stars for which stellar activity and rotation can provide feasible techniques for age-dating purposes (e.g., Simon, Herbig, & Boesgaard Reference Simon, Herbig and Boesgaard1985; Soderblom, Duncan, & Johnson Reference Soderblom, Duncan and Johnson1991; Pace & Pasquini Reference Pace and Pasquini2004; Lachaume et al. Reference Lachaume, Dominik, Lanz and Habing1999; Barnes Reference Barnes2007; Mamajek & Hillenbrand Reference Mamajek and Hillenbrand2008; Epstein & Pinsonneault Reference Epstein and Pinsonneault2014), it may be possible to calibrate parameters such as Q(m FUV − B) in a way that they can be used as a stellar age indicator. Findeisen et al. (Reference Findeisen, Hillenbrand and Soderblom2011) and Shkolnik & Barman (Reference Shkolnik and Barman2014), for example, have previously investigated the change in activity-induced FUV emission with the age of FGK dwarfs and M dwarfs, respectively.
ACKNOWLEDGEMENTS
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. The author gratefully acknowledges the support of award AST-1517791 from the National Science Foundation of the United States. We thank Dr. Jeffrey Linsky for a very helpful referee’s report.
