1 INTRODUCTION
Over the past decade, a new generation of low wide-field radio-frequency (⩽ ~1 GHz) radio telescopes (e.g. LOFAR, van Haarlem et al. Reference van Haarlem2013; MWA, Tingay et al. Reference Tingay2013; PAPER, Parsons et al. Reference Parsons2010) has emerged that require fundamentally different calibration and imaging techniques to traditional radio astronomy. Gone are the days of a simple calibration pointing at a single point source (see Smirnov & Tasse Reference Smirnov and Tasse2015); with fields of 10 s of degrees there are no isolated point sources, and instruments can become confusion limited in 10 s of seconds (Bowman et al. Reference Bowman2013). Indeed, new algorithms to include wide-field effects have been developed (e.g. Rau et al. Reference Rau, Bhatnagar, Voronkov and Cornwell2009) and calibration techniques utilising multiple calibrators from across the sky have been employed (Kazemi et al. Reference Kazemi, Yatawatta and Zaroubi2013).
Creating an all-sky and reliable catalogue with which to calibrate low radio-frequency astronomical data is then a necessary task. The ideal calibration catalogue would span multiple frequencies, providing a reliable spectral shape for each source. It would also be free from any ionospheric positional offsets; it could then be used to correct for ionospheric refraction in future observations (e.g. Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008). To improve our understanding of the radio sky, efforts are currently under way to create ever deeper surveys below 250 MHz in both the northern (MSSS, Heald et al. Reference Heald2015; TGSS ADR1Footnote 1 , Intema et al. Reference Intema, Jagannathan, Mooley and Frail2016, in press) and southern (GLEAM, Wayth et al. Reference Wayth2015) hemispheres.
Each surveying instrument is limited in the frequencies it can access however, so to gain more frequency coverage, multiple catalogues must be combined. There are many examples of cross-matching techniques for radio wavelength data in the literature (e.g. Kimball & Ivezić Reference Kimball and Ivezić2008; Naylor et al. Reference Naylor, Broos and Feigelson2013; Fan et al.Reference Fan, Budavári, Norris and Hopkins2015). Each method seeks to overcome the difficulty in matching sources found from surveys observed with varying instruments and frequencies. Not only does each telescope have its own resolution and sensitivity, but the morphology of each source may change with frequency. Furthermore, each catalogue employs its own source finding algorithm, which inherently has its own strengths and weaknesses. Sophisticated cross-matches are also prevalent in the optical literature (e.g. Haakonsen & Rutledge Reference Haakonsen and Rutledge2009; Pineau et al. Reference Pineau, Motch, Carrera, Della Ceca, Derrière, Michel, Schwope and Watson2011; Bilicki et al. Reference Bilicki2016), which use their own probabilistic positional matching. These cross-matches often focus on finding one single true cross-match between two particular catalogues however, and as such are often necessarily bespoke as to fold in known catalogue selection effects and to achieve the desired science. There are also generic cross-matching tools [such as provided by SExtractor (Bertin & Arnouts Reference Bertin and Arnouts1996)], but of course these are designed to work with optical magnitudes, and so take work to feed radio wavelength catalogues into.
There is a further need for highly accurate radio sky models, for the current generation of low radio-frequency arrays attempting to measure the 21-cm Hydrogen emission line during the Epoch of Reionisation (EoR) (e.g. MWA, LOFAR, PAPER). For these experiments, local galactic and extra-galactic radio sources act as foreground objects, masking the desired signal, and must be removed with exquisite precision (see Furlanetto et al. Reference Furlanetto, Oh and Briggs2006; Morales & Wyithe Reference Morales and Wyithe2010; Pritchard & Loeb Reference Pritchard and Loeb2012, for reviews). As ionospheric offsets are expected to scale with ~ λ2 (e.g. Intema et al. Reference Intema, van der Tol, Cotton, Cohen, van Bemmel and Röttgering2009), and resolution scales with 1/λ, higher frequency observations should have higher positional accuracies. If high frequency instruments can be used to gain precise positional information, allowing accurate removal of these foregrounds, this has a direct bearing on the design and implementation of new instruments for studying the EoR, such as the upcoming SKA_LOW telescope (Dewdney et al. Reference Dewdney, Turner, Millenaar, Mccool, Lazio and Cornwell2013). Using the red-shifted 21-cm line over a range of frequencies allows a probe of spatial scales parallel to the line of sight, as well as over cosmic evolution. It is essential then to also accurately capture the spectral behaviour of foreground sources, as an incorrect subtraction in the frequency domain can affect any derived EoR signal.
The Positional Update and Matching Algorithm (PUMA) was created to meet the needs outlined above. With this software, an approach is developed that utilises both source position and spectral information as matching criterion. Positions can be matched through probabilistic cross-identification, as described in Budavári & Szalay (Reference Budavári and Szalay2008). The desirable quality of the approach outlined in Budavári & Szalay (Reference Budavári and Szalay2008) is that it can easily be scaled to any number of catalogues. Spectral information can be used as a second identification criteria, assuming a spectral model. By focussing purely on low radio frequencies, emission through synchrotron processes can be assumed, allowing the use of a simple power-law model. PUMA has also been created to be as generic as possible, to facilitate an all-sky cross-match that can then have further constraints applied to for any particular science goal.
The rest of the paper is organised as follows. In Section 2, we outline the theory of Bayesian probabilistic cross-identification. In Section 3, we detail the functionality of PUMA, and in Section 4 we use PUMA to create a cross-matched catalogue using real data. Using the outcomes of this cross-match, we create mock catalogues to test the accuracy of PUMA in Section 5. In Section 6, we introduce the 2D Power Spectrum (PS) and test the effects of inaccurate catalogue positions in foreground subtraction when measuring the EoR signal. We discuss our results in Section 7.
2 BAYESIAN POSITIONAL CROSS-MATCHING
In a Bayesian analysis, an hypothesis H can be related to its complementary hypothesis K through the Bayes factor
where D is some measurement set (MS). For this application, D is a set of source positions from multiple catalogues, H is the situation where each catalogue is reporting the same astrophysical source, and K is where they are not. The larger the value of B(H, K|D) then, the stronger the support for the hypothesis H, which in this case indicates a good cross-match. When matching n catalogues, it can be shown (see Budavári & Szalay Reference Budavári and Szalay2008, for further details) that the Bayes factor is given by
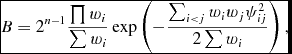 $$\begin{equation}
B = 2^{n-1} \frac{\prod w_i}{\sum w_i} \exp \left( -\frac{\sum _{i<j} w_iw_j\psi ^2_{ij}}{2\sum w_i} \right) ,
\end{equation}$$
$$\begin{equation}
B = 2^{n-1} \frac{\prod w_i}{\sum w_i} \exp \left( -\frac{\sum _{i<j} w_iw_j\psi ^2_{ij}}{2\sum w_i} \right) ,
\end{equation}$$
where ψ2 ij is the angular separation between sources in the ith and jth catalogues, and wi is the weighting for the ith catalogue. This is given by w = 1/σ2, where σ2 is the astrometric precision. This is calculated as
where σRA, σDec are the errors on right ascension and declination, respectively. These errors are usually quoted directly in each source catalogue. The Bayes factor can be related to the posterior probability through
For multiple catalogues, the prior may be calculated through
where the scaled full sky number of sources in each catalogue ν is given by ν i = 4πNi /Ω i , with Ni the number of sources in the sky area Ω i . ν⋆ is the scaled full sky number of sources in the final matched catalogue, with Ωoverlap the region of sky where all matched catalogues overlap. This calculation simply accounts for the source density of each catalogue and how much of the sky all catalogues cover as a way of estimating the prior. The true P(H) depends also on the selection effects of each catalogue; for example, if one catalogue is more sensitive to diffuse emission, the final catalogue may be biased towards brighter flux densities as it is able to detect more emission. There is no simple way for the user to enter these subtle selection effects however, and in the low radio-frequency regime, each catalogue should see similar astrophysical skies, hence this simple prior is retained. Future releases could potentially include a way to incorporate custom selection effects.
3 PUMA
PUMA is an openly available codeFootnote 2 which is free to use. The flow of the matching algorithm is shown in Figure 1. The following sections expand upon the methodology of each step.

Figure 1. The steps and outcomes of the matching process are shown. Yellow boxes represent steps with no criteria applied, cyan represent criteria being applied, and all other colours represent final points. Each cyan box refers to a specific Algorithm, as detailed in Algorithms 1–5. The section labels on the right refer to Sections 3.1–3.3, which detail each step. Each section is performed by a separate script.
As explained in Section 2, P(H|D) gives the posterior probability of a single match, based purely on the positions, positional errors, and source densities of each respective catalogue. However, this does not take in to account the resolution of the differing instruments and surveys used to create each catalogue. It may be the case that a catalogue with lower resolution is indeed describing the same astrophysical source, but averaging over many components, thus measuring a combined flux density and position. Comparing these two catalogues may then yield a very low probability that they are exactly the same source. To account for this, PUMA uses both positional and spectral data to evaluate matches, and allows multiple sources from the same catalogue to be considered in a single cross-match. In this way, any number of catalogues can be matched, but at the cost of using a designated catalogue as a base to cross-match to. In the following section, the following terminology is used:
-
source – a single entry in a catalogue
-
base catalogue – the catalogue upon which all positional cross-matching is performed
-
cross-match combination – defined as a cross-match of sources including only one source from each catalogue
-
repeated catalogue – if more than one source from a single catalogue is matched to a base source, that catalogue is termed a repeated catalogue
The following steps broadly describe the operations carried out by PUMA; they are elaborated upon in Sections 3.1–3.3, respectively:
-
1. Positionally cross-match all catalogues individually to a base catalogue to some user defined cut-off separation. Retain all cross-matches for each base source.
-
2. For each base source, use the cross-matched tables to create every possible cross-match combination including the base source. Calculate P(H|D) for each cross-match combination.
-
3. Apply positional and spectral criteria to each base source and set of matched combinations to identify the best cross-match combination.
Each of these steps is carried out by the scripts cross_match.py, calculate_bayes.py, and create_table.py, respectively. This allows the user greater flexibility in modifying parameters at any stage.
3.1. Initial positional match
The script cross_match.py supports the standard FITS and VOTable formats. Each input catalogue is cross-matched with a designated base catalogue. The final matched catalogue will have a similar source density to the base catalogue, so the user should select the base catalogue that suits their needs. cross_match.py performs two functions. First, relevant information from each catalogue is formatted in a standard way. The user must specify the column names and units of the catalogue, which are then converted and saved in to a ‘simple’ fits table. The required information taken from each catalogue is Source Name; RA J2000 (deg); Error on RA (deg); δ J2000 (deg); Error on δ (deg); Flux density (Jy); Error on Flux density (Jy). Optionally, the user can supply Major Axis (deg); Minor Axis (deg); Position Angle (deg); Flags; Field IDs. The two latter columns are included for the information of the user, but are currently unused by PUMA. These standard tables are then used to perform a positional cross-match within a given cut-off distance using the STILTSFootnote 3 package (Taylor Reference Taylor, Gabriel, Arviset, Ponz and Solano2006). STILTS is the command line version of the cross-matcher used in TOPCAT. cross_match.py uses the information given by the user to create a matched catalogue, where every possible match of the specified catalogue to a source in the base catalogue is saved. Each catalogue is matched to the base catalogue individually, so any number of combinations of catalogues can be used by calculate_bayes.py (see Section 3.2). calculate_bayes.py needs two further things; the source density of each catalogue, and the sky coverage of each catalogue, in order to calculate P(H) [Equation (5)]. cross_match.py internally calculates the sky coverage of each catalogue, fully taking into account the continuous nature of RA co-ordinates. To calculate the source density, the user specifies an area on the sky, bound by lines of RA and Dec for each catalogue. cross_match.py then simply counts the number of sources within this lune. These data are stored in the meta-data of both the individual ‘simple’ tables and the final matched table in a standard way, allowing calculate_bayes.py to automatically read the data. The sky lune to measure the source density within is left to the user’s discretion; an example is shown in Figure 2.

Figure 2. All sources in the VLSSr (Lane et al. Reference Lane, Cotton, van Velzen, Clarke, Kassim, Helmboldt, Lazio and Cohen2014) catalogue are plotted. To calculate the source density of the catalogue, cross_match.py takes given RA and Dec bounds, and counts the number of sources within that area. In this example, the limits are represented by the cyan lines. It is left to the user to pick an area that will give a representative source density of the entire catalogue. For example, if too small an area, or a particularly under-dense area such as that at RA, δ = − 4h, 40°, is selected, an unrepresentative source density will be calculated.
3.2. Bayesian match calculation
The theory outlined in Section 2 is implemented in calculate_bayes.py. This script uses any number of the matched tables created by cross_match.py, combines them, and then calculates a posterior probability for every possible cross-match combination involving each base source.
To calculate the posterior probability [Equation (4)] for each combination, B [Equation (2)] and P(H) [Equation (5)] must be calculated. For the weights in B, the quoted positional errors from each catalogue are used as shown in Equation (3). The rest of the calculation of B is straight forward. To calculate P(H), the number of sources scaled to a full sky coverage for each catalogue ν i , as well as that of the final matched catalogue ν⋆, must be known. These values have already been calculated by cross_match.py, and are read in automatically. Once a combination of potential matches has been formed, calculate_bayes.py identifies the present catalogues, uses the sky coverages measured by cross_match.py to calculate Ωoverlap (which may differ depending on which catalogues are involved in the match), and uses the applicable ν i to calculate P(H). ν⋆ is assumed to be the source density of the base catalogue.
3.3. Matching criteria
The information generated by calculate_bayes.py is used by make_table.py to create a final matched catalogue, by applying the steps shown in the lower section of Figure 1.
The first criteria applied determines which cross-match combinations are deemed as positionally possible. When running make_table.py, the user supplies two variables that dictate what PUMA defines as a possible cross-match combination: P u and θr. P u is a positional probability threshold; if P(H|D) > P u, the cross-match combination is deemed possible regardless of the separation between the individual matched sources. θr is the resolution of the base catalogue (which is usually set to the FWHM of the instrument response of the catalogue). As noted earlier, catalogues with higher resolution may resolve multiple components within the FWHM of a lower resolution catalogue. This may yield low posterior probabilities even though these matches are true; the original assumption in the bayesian treatment is that each catalogue has one true match, and as such doesn’t take into account blending of sources at lower resolutions. PUMA therefore considers any cross-match combination where all sources lie within the resolution of the base catalogue plus error to be possible. Explicitly, any source lying within an error ellipse defined as
where ΔθRA, ΔθDec are the angular offsets of the source from the base source in Right Ascension and Declination, respectively, is considered possible, regardless of the positional probability derived by the bayesian treatment. These positional criteria are initially applied by calculate_bayes.py (Section 3.2). Any matched source from a non-repeated catalogue will be present in all cross-match combinations; as such, these sources are subjected to the above test during the initial calculation of P(H|Di ) for all cross-match combinations associated with a single base source. If all P(H|Di ) < 0.5, matched sources from a non-repeated catalogue are tested using Equation (6). If they fail, the matched sources are discarded, and P(H|Di ) is recalculated.
make_table.py then uses Algorithm 1 to apply these positional tests to matched sources from repeated catalogues, to discard any unlikely cross-match combinations. (All algorithms used in make_table.py can be found in Appendix A).
The successful candidate cross-match combinations are then passed through the following criterion. PUMA splits the matching in to three main regimes; these are explained in more detail in Sections 3.3.1–3.3.3:
-
1. isolated: These are matches where only one cross-match combination is present. These either occur naturally, or when all other cross-match combinations fail the positional matching criteria. PUMA will accept an isolated match if P(H|D) is above some probability threshold, or if the spectral data of the matched sources fit a power law spectral model. If neither of these criteria are met, the match is flagged as rejected.
-
2. dominant: If there are multiple sources from a repeated catalogue that are deemed as possible, each cross-match combination is tested for dominance. This is defined as when the residuals of a fit to a power law spectral model of one combination of sources are at least three times smaller than all other combinations, and the probability of that one combination is larger than all other combinations.
-
3. multiple: If no dominant source is found, the multiple sources from a repeated catalogue are combined in to a single source. These new combined flux densities are then fit with a power law. If the fit is good, the match is accepted with the new combined flux density and positions, generated by combining the sources in the same catalogue. If the combined source fails the spectral test, it is flagged for visual inspection.
3.3.1. Isolated matches
If a base source is labelled as isolated by Algorithm 1, it is passed to Algorithm 2. If P(H|D) ⩾ P
u, the cross-match combination is accepted without further investigation. If P(H|D) < P
u, all sources in the cross-match combination are tested using Equation (6). If all sources pass, the spectral information is interrogated. The flux densities
![]() ${\bm f}$
at frequencies
${\bm f}$
at frequencies
![]() ${\bm \nu }$
are tested by fitting a linear model
${\bm \nu }$
are tested by fitting a linear model
using weighted least squares. This is done using the python package statsmodels Footnote 4 . The residuals of these fits are then investigated to ascertain the deviation of the data from a linear fit. The goal of this spectral fit is to identify large deviations from linearity in log space; it is designed to allow for some curvature of the data. Over small enough frequency ranges, most spectra are expected to follow the linear model in Equation (7), but varying degrees of curvature may be inherent (see Torniainen Reference Torniainen2008, and references therein). Given that there are a limited number of low radio-frequency catalogues to match, the number of data points are often low. This rules out easily using models that account for curvature, as the number of parameters to fit quickly outnumbers the number of data points. As such, the spectral test detailed here has been designed to be simple and robust, and tunable by the user to meet any desired criteria as much as possible.
To test the ‘goodness’ of the fit, the reduced chi-squared value χ2 red is typically inspected, e.g. Hogg et al. (Reference Hogg, Bovy and Lang2010). This value sums the residuals of the fit in units of the variance of the data, and scales for the complexity of the fitted model as
where n is the number of matched catalogues, σ i is quoted error on flux density, Fi is the modelled fit of ln (fi ), and K = (n − p), with p being the number of parameters set (p = 2 for a linear fit). As a general rule, a result of χ2 red < =2 is considered a good fit, as the model lies within twice the observed variance of the data. However, as explored in Andrae et al. (Reference Andrae, Schulze-Hartung and Melchior2010), χ2 red comes with its own uncertainty which grows as the number of data points reduces. Further to this, χ2 red is reliant on the errors on each observations being drawn from a Gaussian distribution. Given that each data set contains data points subject to differing error analyses, the extent to which this is true is difficult to ascertain. Practically, it has been found that χ2 red works well at classifying the fit at low flux densities, where the quoted errors are comparable to the magnitude of the residuals. Conversely, a data set that displays a similar curvature in log space at a much higher flux density yields a far larger χ2 red value, as the errors are small compared to the residuals of the linear fit. Using χ2 red with some cut-off threshold then tends to reject the brightest sources, which are the best sources to calibrate on (e.g. Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008). To include the brightest sources, a second residual metric, ε, is defined as
This residual is designed to test the deviation of a fit from the data in units of the observed valueFootnote 5 . By scaling ε by the number of data points, ε describes the total deviation of the data points from a linear fit as a fraction of the magnitude of the data points. This metric performs well at high flux densities, where the residuals of the fit are small compared to the magnitude of the flux density, but poorly at low flux densities where the residuals are comparable to or larger than the flux densities. χ2 red and ε are then complimentary metrics.
Both are used with cut-off thresholds ε u , χ2 red, u in all spectral tests to accept a cross-match combination. These thresholds can be adjusted by the user to suit their needs. For an isolated match that has P(H|D) < P u but satisfies Equation (6), if either ε2 ⩽ ε2 u or χ2 red ⩽ χred, u 2, the cross-match combination is accepted. Otherwise, the information is stored and labelled as a reject.
3.3.2. Dominant matches
If multiple cross-match combinations are deemed possible by Algorithm 1, they are subjected to a ‘dominance’ test by Algorithm 3. Some sources from a repeated catalogue may be confusing sources that are not associated with the base catalogue source, even though they lie within the resolution of the base source. To test if one single cross-match combination is the correct match, the spectrum of each cross-match combination is fit using the model described by Equation (7). If the residuals of the fit to one combination is three times less than all other fits, it is flagged as possibly dominant. Another criterion is demanded, being P(H|Di ) ⩾ P u and P(H|D i ≠ j < P l), where Di is the positional data of the possibly dominant cross-match combination, and D i ≠ j the data of all other combinations. P l is again a threshold set by the user. These criteria guarantee that the chosen combination has a best fitting spectrum, as well as the most likely positional information. If a cross-match combination passes this test it is accepted and labelled as dominant.
3.3.3. Multiple matches
A group of cross-match combinations that have no clear dominant combination are passed on to Algorithm 4 for a ‘combination’ test. It is possible that sources from a repeated catalogue describe components that are unresolved by the base catalogue. Algorithm 4 tests this by combining the flux density of the sources from the repeated catalogues. It then tests the new spectral data by calculating both ε and χ2 red of the new data. If the new combination has residuals under the residual thresholds, the new cross-match combination is accepted and labelled as a multiple matchFootnote 6 . For each repeated catalogue, a new combined position is found through a weighting scheme described by
where n is the number of repeated catalogue sources, and f the flux density of each source. These weights are applied to create the new RA position and error as
this is similarly applied for δ. If the combining test fails, the group source information is labelled as an eyeball.
Splitting test – combining sources as described above confines the output catalogue to the resolution of the base catalogue. make_table.py also comes with an option to ‘split’ the combined sources, which is handled by Algorithm 5. If the sources from each repeated catalogue are separated by a distance greater than some user specified cut-off, d split, PUMA will attempt to split the combined source in to components. If there is more than one catalogue with repeated sources, PUMA currently requires that each repeated catalogue have the same number of sources matched, simplifying the matching of these repeated sources. The repeated sources from each repeated catalogue are matched by distance, to create new cross-match combination components. The flux density from each catalogue that had only one source matched is then split in to components to match these new cross-match combination components, based on the following weighting scheme. For each catalogue m of n repeated sources, weights are created and averaged as
where w j, i is the wi [Equation (10)] weight in the jth catalogue. The flux density of each single catalogue match source is then split as
where f s is the flux density of the source, and wk is a vector of length n of weights w k. Applying the weights in this manner uses all the information from the repeated catalogues to create an accurate spectral energy distribution (SED) for each component.
Once an SED has been created for each component, they are spectrally tested as in Algorithm 3. If all components pass the spectral test, the sources are accepted. Each component is given a name based on the position of the original base source, with a letter appended to distinguish between components. If one or more components fail the spectral test, the source is flagged to investigate by eye.
3.4. Final matched table
Once make_table.py has applied the algorithms described in Section 3.3, a list of accepted sources is left. These are output to a either a FITS or VOTable, the contents of which are described in Table 1. Two positions are reported; that of the original base source, and an ‘updated’ position. The user supplies a ranking of all matched catalogues. The position of the highest ranked source in a cross-match combination is then reported as this updated position. This ranking can be set to the needs of the user, but the highest rank would usually be given to the catalogue with the highest angular resolution and least affected by ionospheric effects. If this highest ranked matched source was created by combining sources as described in Section 3.3.3, the flux density weighted centroid given by Equation (11) is reported.
Table 1. Details of the content of the final matched catalogue output by make_table.py

As described in Equation (7), a model of
![]() $ \ln ({\bm f}) = \alpha \ln ({\bm \nu }) + \beta$
is fit to each combination. When this fit is performed, the frequencies are entered in MHz and the flux densities in Jy. When performing the linear fit, the package statsmodels also outputs the standard error of the fitted parameters σ2
β, σ2
α. The spectral index and error, α and σα are both reported in the final matched catalogue. If desired by the user, the fit is used to extrapolate a flux density and error at the frequency of the base catalogue through the equations:
$ \ln ({\bm f}) = \alpha \ln ({\bm \nu }) + \beta$
is fit to each combination. When this fit is performed, the frequencies are entered in MHz and the flux densities in Jy. When performing the linear fit, the package statsmodels also outputs the standard error of the fitted parameters σ2
β, σ2
α. The spectral index and error, α and σα are both reported in the final matched catalogue. If desired by the user, the fit is used to extrapolate a flux density and error at the frequency of the base catalogue through the equations:
where again the frequency is in MHz.
The final table only includes sources that were accepted. For all base sources classified as reject or eyeball, all possible cross-match combinations are printed out to a text file, which can be used for further investigation. If selected, PUMA will print out a summary of the matching statistics to a text file. The PUMA package also comes with a plotting script, plot_outcomes.py, which has multiple search criteria in built (for examples, see Figures 4–8). For detailed information on the running of, the outputs, and plotting capabilities of PUMA, refer to the online documentation.
4 CREATING A COMBINED CATALOGUE
During the first incarnation of PUMA, the MWA had been collecting EoR data for months already. The software being used by the Australian MWA EoR pipeline, the Real Time System (the RTS; Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008, in preparation), requires an input source catalogue to generate a sky model for visibility calibration and source subtraction. Previously, the Molonglo Reference Catalogue (the MRC, Large et al. Reference Large, Mills, Little, Crawford and Sutton1981) was used. Being a shallow and directed survey, the MRC is only complete to ~ 1 Jy beam−1, and reports a single frequency of 408 MHz. The MWA observes between 80 and 300 MHz, so an assumed spectral index of − 0.7 was used to extrapolate the sources to the desired frequencies.
The MWA Commissioning Survey (MWACS, Hurley-Walker et al. Reference Hurley-Walker2014) was undertaken to provide a better model of the sky at these frequencies, during the commissioning phase of the MWA, when the instrument had less elements and thus less sensitivity and poorer resolution. Given that accurate positions were unobtainable with shorter baselines and a new array to calibrate, MWACS was limited in its accuracy, and therefore a prime candidate for testing PUMA.
To best calibrate and remove sources from a target field, a source catalogue must cover the entire field. The first science field targeted for EoR by the MWA was labelled EoR0, centred at 0 h , − 27°. Due to the large primary beam of the MWA tile response (e.g. Tingay et al. Reference Tingay2013), good knowledge of the sky is needed to at least 2 h distance from field centre (see Figure 3). Further, due to the grating side lobes of the primary beam, power from sources as far as the horizon can enter the visibilities, necessitating a catalogue that covers the entire sky. MWACS unfortunately only extends up to a declination of ~ −15° . To get the best combination between depth and coverage at the correct frequencies, it was decided to use MWACS as the base catalogue, and fill any missing sky coverage with MRC as a base.

Figure 3. The overall sky coverage of each catalogue is shown in (a). Apart from MRC, all catalogues only partially cover the MWACS field, which is emphasised by the zoom in on the EoR0 field shown in (b). A contour plot shows the MWA primary beam at 180 MHz, with EoR0 at zenith. The first four grating side lobes are clearly visible outside the dashed circle which represents 2 h from field centre.
The following catalogues were used to cross-match: The 74 MHz Very Large Array Low Frequency Sky Survey redux (VLSSr, Lane et al. Reference Lane, Cotton, Helmboldt and Kassim2012); the 843 MHz Sydney University Molonglo Sky Survey (SUMSS, Mauch et al. Reference Mauch, Murphy, Buttery, Curran, Hunstead, Piestrzynski, Robertson and Sadler2003); and the 1.4 GHz NRAO VLA Sky Survey (NVSS, Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998). These surveys were selected due to their frequencies and sky coverage (see Figure 3 and Table 2).
Table 2. General characteristics of the base and cross-matching catalogues. The quoted beam widths for MWACS and MRC and indicative only, as they vary across the sky and with frequency.

4.1. Running PUMA
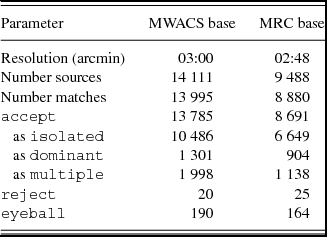
PUMA was run first using MWACS as a base and matching to all other catalogues, then again using any MRC sources lying outside of the MWACS field as a base. In both cases, the following parameters were used: P u = 0.95; P l = 0.8; χ2 red, u = 10; εu = 0.1. These settings were decided upon after investigating matching outcomes; the chosen spectral fitting cut-offs allow for some inherent curvature of the SED, whilst still failing for large deviations from linearity. For an exploration of the effect of these parameters on the PUMA classifications, see Appendix B. As the splitting test outlined in Section 3.3.3 only covers the most simple cases of repeated catalogue matches, this option was not invoked during this analysis. The order of catalogue position preferred was set as NVSS; SUMSS; MWACS/MRC. VLSSr was not selected as a correcting catalogue as it suffered from ionospheric effects and has already been positionally fit using NVSS (see Cohen et al. Reference Cohen, Lane, Cotton, Kassim, Lazio, Perley, Condon and Erickson2007; Lane et al. Reference Lane, Cotton, van Velzen, Clarke, Kassim, Helmboldt, Lazio and Cohen2014, for details). The matching statistics from both runs are shown in Table 3, showing that overall 98.6% of sources were accepted by PUMA and automatically matched. Table 2 also shows that some MWACS or MRC sources found no match at all with other catalogues. After investigation, the vast majority of these sources were found to lie near the galactic plane in the southern hemisphere. SUMSS does not cover the sky over |b| < 10°; as only SUMSS and MRC extend below δ = −40°, this accounts for the missing matches. Given the galactic plane lies more than 4 h away at the declinations applicable to the EoR0 field, these sources were ignored.
Table 3. The settings used and matching statistics obtained when running PUMA on real data. The number of sources shows the number of base catalogue sources for each case, and the number of matches the instances where a match to at least one catalogue was found.
4.2. PUMA outcomes
Of the 22 476 automatically accepted matches, 76% were classified as isolated, 10% as dominant, and 14% as multiple. Figures 4–8 show example PUMA outcomes for each classification. In each Figure, the two left-hand plots show the positional and spectral information fed into PUMA. If a catalogue included Gaussian fit parameters for sources, these are plotted for instruction only; they were not used by PUMA during the cross-matching process. The plots on the right-hand side then show each cross-match combination of the matched sources, with the pertinent matching probability and spectral fit residuals.

Figure 4. An example of an accepted isolated match. As there is only one possible combination of sources, and that combination has P 1 > P u, the cross-match combination is accepted without investigating the SED.

Figure 5. An example of an accepted dominant match. There are two NVSS sources well within the resolution of the base MWACS source. Given the positional error on the MWACS source, both cross-match combinations yield high positional probabilities. The SEDs of both cross-match combinations are investigated, and it is found that P 1 > P u, P 2 < P l as well as cross-match combination 1 having far lower residuals to a power law than cross-match combination 2. This results in match 1 being selected as the correct match.

Figure 6. An example of an accepted multiple match. In this example, both cross-match combinations 2 and 12 yield P > P u and so there is no dominant match. Instead, all flux densities are combined, and the new SED tested with a power law fit. As the fit is deemed to be good, the source is accepted, and the weighted NVSS position (orange star) is used as the corrected position.

Figure 7. An example of an reject position match. Both SUMSS source lie outside of the resolution of the MWACS catalogue plus the positional error of the MWACS source. As P 1, 2 < P u, all cross-match combinations are deemed improbable and are rejected. Further investigation of cross-matches such as these are best diagnosed in conjunction with postage stamp images such as shown in Figure 11.

Figure 8. An example of an eyeball multiple match. Many cross-match combinations lie outside of the resolution plus error of the base MWACS source, with no dominant combination. A sum of the flux densities of the matched sources that passed the positional criteria yields a poor fit to a power law, and so the MWACS source is not accepted and labelled to eyeball. Again, further investigation of cross-matches such as these are best diagnosed in conjunction with postage stamp images such as shown in Figure 11.
4.2.1. SI distribution
To check for any systematic biases in the differing matching classifications, the SI distributions of each classification were compared in Figure 9a. The isolated and multiple classifications report near identical distributions, with the dominant resulting in a similar distribution centred at a slightly steeper SI. There are multiple factors that could account for this offset, two contributory factors of which are: the dominance test could consistently choose dominant sources when it should be combining flux densities, thus under-estimating flux densities at high frequencies; the weighted least squares fit is strongly biased to higher flux densities due to the smaller associated errors, and so small changes in flux density at those frequencies greatly affect the fit. To do any accurate modelling of spectra (e.g. Callingham et al. Reference Callingham2015), it is essential to remove confusing sources. This possible steepening is further investigated in Section 5.2.

Figure 9. (a) kernel density estimate of the SI distribution of each PUMA classification. The median and absolute median deviation of each distribution is quoted in the legend. (b) A histogram of the offsets of MWACS sources to either NVSS or SUMSS found by PUMA, including all match types except from eyeball and reject. We find similar positional offset behaviour from NVSS and SUMSS as is described in Hurley-Walker et al. (Reference Hurley-Walker2014).
4.2.2. Positional offsets
The positional offsets found when considering only cross-matches with MWACS as a base that were accepted by PUMA are shown in Figure 9b. The positional offsets for all isolated sources surrounding the EoR0 field are shown in Figure 10. PUMA classifications are most useful in this instance for quickly flagging out confused cross-matches; the isolated matches can then be used to investigate inherent catalogue properties.

Figure 10. The positional offset found to either NVSS or SUMSS from either MWACS or MRC is shown. The edge of the MWACS field is clearly seen at δ = −15°. The positional agreement with MRC is excellent, most likely due to MRC only containing bright sources. As explained in Hurley-Walker et al. (Reference Hurley-Walker2014), the positional offsets to MWACS vary with RA. The MWACS survey was taken over two declination strips, the effect of which appears to be visible in the plot, with the decrease in offset density at around δ = −37°. There are hints of an overall north-east offset in the upper declination strip; this is further investigated in Carroll et al. (Reference Carroll2016). Coherent patches of positional offsets are consistent with a phase gradient introduced by ionospheric effects. As these would vary over a night, the offsets seen here could well be ionospheric.
4.3. eyeball and reject sources
399 sources were not automatically catalogued by PUMA. As this matching process was run with the EoR0 field in mind, it was decided to include sources within 2 h of the EoR0 field centre, leaving 74 sources to investigate. For each flagged source, postage stamp images of available relevant catalogues were obtained and plotted. These were used in conjunction with catalogue information to make an informed decision on a cross-match. An example of this process is shown in Figure 11. The MWA data simulated in Section 6 was taken when the MWA had greater resolution (~ 2.3 arcmin) than when MWACS was created. For this reason, any MWACS source that was matched to multiple components that were separated by an angular distance that would be resolved at 2.3 arcmin were split into multiple catalogue entries in a bid to reduce residuals after source subtraction when using real data.

Figure 11. An example of the matching process for extended sources is shown. The two upper left panels show all information given to PUMA. The bottom three panels show postage stamp images of the three matched catalogues, with the reported catalogues over-plotted, along with the MWACS source. In this case, the source reported in the VLSSr catalogue does not realistically match the VLSSr image. This artificially creates a curved SED, which causes PUMA to label this match an eyeball. Given the doubt cast on the VLSSr source, it is ignored in the cross-match, and the SUMSS and NVSS sources that seem positionally reasonable are combined and matched. This gives a realistic positional match as well as spectra.
5 TESTING PUMA
To test the fidelity of PUMA, it is necessary to know the true sky. The known positional and SI distributions can then be used to compare to the positional corrections and SI distribution derived by PUMA. In this section, a point source sky model is created using the NVSS catalogue. It is used to create simulated sky images as seen by the five telescopes for the catalogues matched in Section 4. Source-finding is then applied to these images to create five mock catalogues on which to test PUMA. The two criteria used to test PUMA is the recovery of accurate positions and SI.
5.1. Mock catalogues
5.1.1. NVSS sky model
NVSS catalogued positions and flux densities were selected from a fiducial lune of sky, bounded by 0.0° ⩽ RA ⩽ 30.0° and − 40.0° ⩽ δ ⩽ −30.0°. This patch of sky was chosen as it lies in the overlap region between SUMSS and NVSS, and to generate enough sources to have statistical significance when testing PUMA. To get a realistic SI for each point source, a simple positional cross-match was performed to SUMSS, with a cut-off of half the beam width of the NVSS survey (22.5 arcsec). Any NVSS source without a match was assigned a random SI, drawn from a gaussian distribution with μ = −0.8, σ = 0.2, to reflect the SI distributions seen in Figure 9a.
5.1.2. Simulated sky images
The selected NVSS sources were used to populate a point source sky array model at the frequencies of the five catalogues listed in Table 2, extrapolating the flux densities using the assigned SI. The astropy.convolution Footnote 7 python library was then used to convolve the sky array with a Gaussian kernel, set to have a full width half maximum value equal to the beam width listed in Table 2. In doing so, the restoring phase of a CLEAN (Högbom Reference Högbom1974) image process is mimickedFootnote 8 ; this process is typically applied to interferometric radio data to remove the instrument response from the image, with the restored image then used for source finding. Gaussian noise was added to the image based on reported image rms from the literature of each catalogue (see Table 2), to make the source finding as realistic as possible. Figure 12 shows a comparison the simulated NVSS to sky to the real data, as well as the simulated MWACS image.

Figure 12. A comparison of a real NVSS postage stamp image (upper panel) and a simulated NVSS postage stamp (central panel), created as described in Section 5.1.2. The same area of sky is also shown as simulated to mimic an MWACS postage stamp (lower panel).
5.1.3. Source finding and SI derivation
Source finding was performed using the PyBDSM packageFootnote 9 , which is designed to perform source finding on radio interferometric images, and is capable of fitting Gaussians, Shapelets, and Wavelets to an image. In this analysis, only Gaussians were fit to the mock catalogues. To derive the SI of sources found for the mock MWACS catalogue, five extra sky images were made at 74, 180, 408, 843, and 1 400 MHz, without any noise. The Gaussian fit parameters found by PyBDSM for the mock MWACS catalogue were then used to measure the flux density for each source in the noiseless images, by summing the pixels that were bound by the Gaussian fit. These measured noiseless flux densities were then fit using least squares to calculate an expected SI. To ensure that flux densities used to estimate the SI and those used to test PUMA in Section 5.2 are consistent, the method of generating a noiseless image and directly summing to measure a flux density was applied to all the mock catalogues; all positional information and errors derived by PyBDSM were retained.
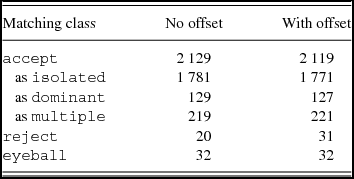
5.2. PUMA comparison
PUMA was run using the mock MWACS catalogue as a base in the same way as described in Section 4.1. The matching outcomes are summarised in Table 4. The source positions and SI found in Section 5.1.3 for the mock MWACS sources were taken to be the ‘true’ source characteristics on which to compare the outputs of PUMA to. To test the robustness of the positional offset recovery, PUMA was run a second time, after random positional offsets were added to the mock MWACS catalogue. The derived positional offsets from the PyBDSM positions and calculated SI are shown for each PUMA classification in Figure 13. For comparison, the derived SI from running a simple nearest-neighbour cross-match within 90 arcsec, approximating the FMHW of the mock MWACS beam, is shown. This highlights the power of combining high resolution catalogue data; PUMA reliably retrieves the correct SI for mulitple matches, whereas a simple nearest-neighbour match consistently retrieves a steeper SI. Figure 13 shows that PUMA behaves the same in the presence of unaccounted positional errors, on top of those quoted by PyBDSM, given the same positional and SI distributions retrieved in both runs. The positional offsets found for isolated sources are small, and are smaller than the PYBDSM errors. Given this, in conjunction with the coherent ionospheric offsets found in the MWACS catalogue, as well as the coherent offsets found by PUMA in Carroll et al. (Reference Carroll2016), it is clear that for isolated sources, the positional corrections are indeed improving the positional accuracy of the source, whilst reliably reported the correct SI.

Figure 13. The positional corrections (left column) and SI distributions (right column) derived by PUMA when matching mock catalogues, split in to isolated, dominant, and multiple (top, middle, and bottom rows, respectively). For every distribution, the median and median absolute deviation is quoted in the legend. In the left-hand column, the PUMA positional corrections found when using the PyBDSM mock MWACS positions (no offset) and with positional offsets added (with offset) are shown. The added positional offsets (injected offsets), as well as the PyBDSM reported errors are also plotted. In the right-hand column, the PUMA SI distributions are again shown for both the PyBDSM MWACS and the perturbed positions, compared to expected SI distribution as derived in Section 5.1.3, by finding the flux density from noiseless mock MWACS images. An SI distribution is also shown by performing a nearest neighbour match to the PyBDSM MWACS positions to within 90 arcsec. The PUMA classifications were taken from the match with the original PyBDSM MWACS positions; only matches which were accepted by both PUMA runs (offset and no offset) are plotted for a direct comparison.
Table 4. The matching classifications found by PUMA when matching the mock catalogues (No offset), along with the case where positional errors were introduced into the mock MWACS catalogue (With offset).
If dominant cases are purely discriminating chance alignments of physically unrelated sources, we might expect the positional offsets derived for isolated and dominant to be the same. The distributions are indeed similar, however the dominant distribution shows a median offset of around double that of the isolated cases. This is likely due to the confusing source(s) contributing some flux density to the lower resolution catalogue sources; this blending skews the positional of the base catalogue source. The dominant distribution is closer to the isolated distribution than the multiple distribution however, which lends confidence that the dominant class should be kept separate to the multiple. As seen in Figure 9a, a slight steepening of the SI distribution is shown for dominant matches. This is also likely due to some blending of sources, which would manifest as an over-estimation of the lower resolution (usually lower frequency) flux density, naturally causing a steepening in the SI. However, as the dominant component should be driving the spectral behaviour of the source at the base catalogue frequencies, this reported SI should realistically describe the behaviour of the source as seen by the base catalogue.
Figure 13 shows that the positional offsets found for multiple matches are comparatively large. As defined in Section 3.3.3, the positional offsets here are derived from the flux density weighted centre of the combined higher resolution catalogue sources: These offsets can then be dominated by the differences in morphology at differing frequencies. As such these positional corrections may not actually be improvements at the frequency of the base catalogue. The method clearly works when estimating the SI however, so it remains up to the user as to which position is appropriate for their desired science case.
6 SIMULATIONS OF FOREGROUND REMOVAL TOWARDS AN EOR DETECTION
The red-shifted 21-cm Hydrogen emission line (HI line) is a tracer of neutral hydrogen (HI) and as such can be used to measure the effect of ionising radiation on HI during the EoR, and can be used to constrain the timing of the epoch as well as the nature of the first ionising sources. As stated in Section 1, extra-galactic radio sources emit at the same frequencies and must either be removed or avoided to make a detection. The MWA EoR pipelines have opted for direct foreground removal in the case of point sources (Jacobs et al. Reference Jacobs2016). In this section, we create simulations to investigate how subtracting point sources with inaccurate astrometric information will effect a measurement of the EoR signal.
Current generation low-frequency radio arrays are not sensitive enough to directly image the HI line from the EoR. Instead there is a focus on making a statistical measurement through a PS analysis of the emission of large sky areas. The final measurement will be a 3D spherically averagedFootnote 10 to 1D PS, but the 2D PS serves as a useful instrument and data diagnostic tool. The 2D PS plots variations in measured power across the frequency response of the instrument against its angular response across the sky, and as such different instrumental effects as well as astrophysical signals should inhabit different parts of the 2D PS (e.g. Morales et al. Reference Morales, Hazelton, Sullivan and Beardsley2012). Of particular interest in the literature is the ‘wedge’ (see Datta et al. Reference Datta, Bowman and Carilli2010; Parsons et al. Reference Parsons, Pober, McQuinn, Jacobs and Aguirre2012; Vedantham et al. Reference Vedantham, Udaya Shankar and Subrahmanyan2012; Hazelton et al. Reference Hazelton, Morales and Sullivan2013), a region in which the emission of point sources is expected to be confined [although some power from point sources should exist outside of this wedge, i.e. Thyagarajan et al. (Reference Thyagarajan2013)]. The area most devoid of foreground contamination is known as the ‘window’, and is targeted for an EoR detection.
A PS estimation of the EoR requires removal or avoidance of bright foregrounds including point sources at the same frequencies as the red-shifted 21-cm line. If implemented with sufficient accuracy, direct point source removal promises to open up the largest measurement space in the 2D PS (Pober et al. Reference Pober2014). Trott et al. have studied the effect of point source removal in the presence of inaccuracies in the data set itself (Trott et al. Reference Trott, Wayth and Tingay2012). Given the need for accuracy outlined here, this analysis investigates the effect of positional inaccuracies in the calibration and source removal catalogues on the 2D PS. The focus here is to probe where power is removed from the 2D PS, and how that could affect any possible EoR detection. The drawbacks to testing on real data are numerous; however, a real instrument can introduce random and systematic errors; the ionosphere is a constantly changing source of error; the true sky brightness distribution is actually unknown, and consists of point like and diffuse emission with varying spectral behaviours. The latter is the biggest obstacle for this experiment, so simulated visibilities were created using OSKARFootnote 11 (Mort et al. Reference Mort, Dulwich, Salvini, Adami and Jones2010). In this manner, the input data could be completely understood and so the effects of positional inaccuracies be isolated.
To achieve this, two source catalogues were created from the PUMA outputs; one using the original MWACS positionFootnote 12 , and a second with the updated PUMA position. We refer to these as the MWACS source list and the PUMA source list, respectively. Both source lists were given exactly the same spectral information. The Australian MWA EoR pipeline was used: all calibration and source subtraction was run using the RTS (Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008), and all 2D PS were made using the Cosmological HI Power Spectrum Estimator (CHIPS, Trott et al. Reference Trott2016). The RTS utilises clustered source calibration (Kazemi et al. Reference Kazemi, Yatawatta and Zaroubi2013), and can either peel (individually calibrate and subtract a source) or subtract as many sources as required.
In Section 6.1, we outline the MWA observations that were the basis of our simulations; simulating real observations allowed comparison with data as shown in Figure 14. In Section 6.2, we detail the OSKAR simulations used to generate MWA-like data. In Section 6.3, we present the results of our analysis and the effects of positionally inaccurate source subtraction on the 2D PS.

Figure 14. Four ‘dirty’ (with the synthesised interferometric beam still convolved with the sky brightness) naturally weighted images are shown for an integration of 64 s of data across the entire 30 MHz bandwidth. The left-hand column shows OSKAR simulations, with the right hand showing MWA data. The top row shows calibrated data, and the bottom data with the same 1 000 sources from the PUMA sky model created in Section 4 subtracted. (a) and (b) reveal the excellent agreement of the synthesised beam created by OSKAR and the real MWA. (c) and (d) reveal the biggest difference in the sky, that being the diffuse emission clearly visible in (d); diffuse emission is mostly due to synchrotron emission from cosmic rays interacting local with galactic field lines (Ginzburg & Syrovatsk Reference Ginzburg and Syrovatsk1969).
6.1. The MWA
The MWA telescope consists of 128 elements, each of which is made of 16 cross-dipole antennas in a 4 × 4 grid. The dipoles in each of these ‘tiles’ are electronically beam-formed, forming a quantised set of primary beam pointings. The signal path of the MWA extracts 30.72 MHz of bandwidth, which it splits into 768 fine channels of 40 kHz in a Polyphase Filterbank (PFB). These data are combined and averaged to 0.5 s in the correlator (see Ord et al. Reference Ord2015, for further details).
The MWA is located on the Murchison Radio Observatory site, which is extremely radio-quiet (Offringa et al. Reference Offringa2015; Allison et al. Reference Allison2015); even so some radio interference remains so all data was flagged using COTTER (see Offringa et al. Reference Offringa2015). Due to the bandpass imparted by the PFB, 5 out of every 32 fine channels are also flagged.
A fiducial night of data was selected to test the reduction pipelines employed by the MWA EoR analysis team (see Jacobs et al. Reference Jacobs2016, for details). A subset of 1 h of these observations were selected for testing here, chosen for balance between integration time and processing costs. The EoR0 field stays within one pointing of the MWA for approximately half an hour, giving two pointings (and therefore two beam patterns) in the dataset. The zenith pointing (e.g. Figure 3b) and one pointing 6.8° off zenith were chosen, as the MWA beam is best understood at zenith (Neben et al. Reference Neben2015).
6.2. OSKAR simulations
OSKAR was primarily created to simulate data from SKA-like interferometric arrays. Accurately simulating visibilities is a computationally expensive endeavour, due to multiple Fourier Transforms and gridding steps. OSKAR deals with this by assigning each point source in the sky model to a thread on a GPU, greatly speeding up the process. Importantly, OSKAR takes into account wide-field effects (caused by the curvature of the sky), which are necessary given the > 30° field of view of the MWA.
OSKAR is capable of beam-forming groups of receiver elements, such as those in an MWA tile. To be explicit, for these simulations, OSKAR was given the 4 × 4 grid pattern of an MWA tile, and told there was a cross-dipole antenna at each point. OSKAR then uses an analytic model for each cross-dipole and combines the response of all 16 antennas with appropriate delays to mimic the MWA primary beam. This is slightly different from the model use by the RTS (Sutinjo et al. Reference Sutinjo, Padhi, Wayth, Hall, Tingay, O’Sullivan and Lenc2014), which includes mutual coupling between the dipoles.
OSKAR simulations were set up to exactly mimic the MWA observations detailed in 6.1; the one difference being the correlator was set to sample at 2 s rather than the half second in the MWA data, which reduced the computational load by 4. The PUMA source list was used as an input sky model. When supplying the RTS with a calibration or peeling source list, the RTS reads in given flux densities at specified frequencies, and then extrapolates a sky model to the frequency of the data by fitting a power law spectral model between the two closest given frequencies. To ensure perfect source subtraction when using the PUMA source list positions, the sky model input to OSKAR was extrapolated in the same way to all frequencies.
A number of steps were necessary to run RTS on OSKAR simulations. OSKAR outputs either a native binary format file or a CASA MSFootnote 13 . The RTS is capable of reading either native MWA outputs or UVFITS Footnote 14 files. Routines already exist in casapy to transform a MS into a UVFITS file. Due to differing coordinate definitions and a frequency related issue however these UVFITS files still need editing (achieved here using python), leaving the final pipeline as:
One final complication is that the MWA correlator is slightly unusual in the fact that is does not fringe track—this being the procedure of adding phase delays within the signal path to ensure the data is fully coherent in the pointing direction (see Ch.2, Taylor et al. Reference Taylor, Carilli, Perley, Taylor, Carilli and Perley1999, for the theory of phase tracking). The correlator in OSKAR is hard-coded to phase track, and so these phase rotations must be undone in the final python script. Furthermore, each simulated MWA tile is beam-formed in the direction of the phase centre, which is specified in RA, δ. As the real MWA beam only points to a specific HA, δ during an observation, a new RA, δ must be entered for each time step. This combined with the frequency editing means OSKAR has to be run separately for every fine channel and time step. Given an input catalogue of 22 618 sources, it takes ~ 6 h using 24 NVIDIA Tesla C2090s GPUsFootnote 15 to simulate a 2 min MWA observation. A comparison between real MWA data and an OSKAR simulation is shown in Figure 14.
6.3. Results
The left and central plots in Figure 15 show 2D PS obtained after processing the OSKAR simulations through the Australian MWA pipeline. Each plot shows the power as a function of k-modes derived from angular scales upon the sky (k ⊥) and those derived from the frequency response of the instrument (k ∥). The solid diagonal line is set to represent the expected location of foregrounds within the main lobe of the MWA primary beam, and the dashed diagonal line the contribution of foreground sources at the horizon limit.

Figure 15. Two 2D power spectra are shown (left and centre), both created using the XX polarisation and the entire simulated hour of data. Each plot shows amplitude as a function of k-modes perpendicular to the line of sight (derived from angular scales on the sky, k ⊥) horizontally, and k-modes parallel to the line of sight (derived from frequency response, k ∥) vertically. The plot on the left shows the power before source subtraction, and the centre after 1 000 sources have been subtracted. The plot on the right shows the difference plot of the 2D power spectra, with the 1 000 source spectra subtracted from the spectra without source subtraction. Blue in this case shows more power being present before source subtraction. The absolute scale shown here is not the most instructive part of these plots as an interferometer naturally measures variations about a mean; the relative power as a function of k-space however informs us where foreground power is being removed from.
Given that the visibilities only contain point sources the calibration solutions were excellent when calibrating both with the PUMA and MWACS source lists. The PS in Figure 15 display the characteristic wedge shaped power from point sources, apparent in the saturated bottom right corner of each plot. The horizontal bands of power in the EoR window are due to the spectral behaviour of the flagged fine channels (see Section 6.1) convolving with the power from the wedge. When searching for calibration or data analysis effects in the 2D PS, it is often instructive to create difference plots, that being one 2D PS subtracted from another (e.g. Beardsley et al. Reference Beardsley2016, in press). An example difference plot is shown on the right in Figure 15.
After processing through CHIPS with various subsets of the simulated data to demonstrate the effect of subtracting sources with positional inaccuracies, we discovered a competing differencing effect inherent to the data: Each pointing observed a fundamentally different sky. For this reason, we split our results into zenith and off-zenith pointings. We include a comparison of zenith and off-zenith simulated data in this section for completeness.
The effect of subtracting sources with positional inaccuracies is shown in Figure 16. This shows the difference between subtracting sources from the PUMA and MWACS source list. The PS are compared pointing by pointing to negate the pointing effect described above. The behaviours observed at low k ⊥, k ∥ are inconsistent, which is likely due to the poor sampling that exists here; this part of the PS corresponds to large angular and spectral scales, which are limited due to the field of view and bandpass. For the rest of the PS, it is seen consistently over each pointing and polarisation that subtraction with exact source positions not only overall removes more power from the wedge, but also from the window as well. As stated, the absolute value of the power in the 2D PS shown here are not instructive, but the relative differences in power seen in the window are within ~ 1–2 orders of magnitudes of that seen in Figure 15 Footnote 16 . Given that the EoR signal is thought to be ~ 3 orders of magnitude dimmer than these foregrounds, this highlights the need for the best possible foreground models to reduce the leakage of point sources from the wedge into the window (i.e. Offringa et al. Reference Offringa2016).

Figure 16. Four difference PS are shown to contrast data processed with the PUMA source list to the MWACS source list: (a) Zenith pointing, PUMA source list—MWACS source list, XX polarisation; (b) Zenith pointing, PUMA source list—MWACS source list, YY polarisation; (c) Off-zenith pointing, PUMA source list—MWACS source list, XX polarisation; (d) Off-zenith pointing, PUMA source list—MWACS source list, YY polarisation. In each case, blue represents more power for data with exact positional source subtraction opposed to offset positional subtraction, and red less power.
The differences in the sky seen by differing pointings is shown in Figure 17. These plots demonstrate that the sky is fundamentally sampled differently through the zenith and off-zenith pointings, due to a combination of the beam pattern differing between pointings, creating grating side lobes which contribute power at different amplitudes from different parts of the sky, along with a sky that is changing with time. This is perhaps most apparent in Figures 17c and d, shown by the diagonal blue stripe bound by the solid and dashed lines. Power in this area of the PS comes from sources close to the horizon (see Pober et al. Reference Pober2016, and references therein); the differences caused here by the changed horizon between pointings become apparent after subtracting the 1 000 brightest sources.

Figure 17. Four difference PS for data processed using the PUMA source list only, each representing half an hour of data: (a) No peeling, zenith—off-zenith, XX polarisation; (b) No peeling, zenith—off-zenith, YY polarisation; (c) 1 000 sources peeled, zenith—off-zenith, XX polarisation; (d) 1 000 sources peeled, zenith—off-zenith, YY polarisation. In each case, blue represents more power in a zenith pointing, and red less power. The top row shows there is overall more power seen for the zenith pointing before source subtraction, and the bottom rows show there is overall less power after subtracting the 1 000 brightest sources. Again, the absolute value of the power is less important than the distribution of power throughout k-space.
7 DISCUSSION
We have developed software that is capable of automatically cross-matching ~ 99% of the MWACS catalogue to other radio-wavelength catalogues of differing resolutions, necessitating the need to deal with confused matching. Using simplistic simulations, we tested the matching results of PUMA and found it able to reliably recover a known SI distribution, and to be robust to typical ionospheric positional offsets prevalent in low radio-frequency observations. This high fidelity of matching is important for the current generation of low radio-frequency surveys (such as GLEAM and MSSS), which will produce catalogues on orders of ~ 105 sources, and more so for future SKA-type surveys which may produce ~ 106. With this in mind, the software has been designed to be tunable to the needs of the desired application, with several manually adjustable parameters. Even so, these algorithms will need to be further developed to save manually inspecting over 104 sourcesFootnote 17 (although these numbers of sources are routinely inspected spread over a large team for a wide-field optical survey).
After applying PUMA, the impact of gaining more precise positional information from higher frequency radio catalogues was investigated through OSKAR simulations. This was achieved by studying the effects of removing sources from interferometric visibilities and investigating the resulting 2D PS. It was found that when subtracting sources with exactly correct positions, more power was not only subtracted from the wedge but also from the window, the measurement space in which an EoR detection could potentially be made. This adds weight to the growing argument in the literature to the most accurate possible sky models.
Whilst this paper concentrates on the benefits of this methodology for creating foreground models for EoR science, it of course has wider applications, particularly for population studies of radio galaxies, and for verification of sources during catalogue creation. It also has implications for baseline configurations for future EoR arrays: If the true positions of sources can be established from higher frequency information, longer baselines may not be necessary, reducing cost and allowing for more short baselines, increasing the sensitivity of the array to the spatial scales at which the EoR signal can be measured.
ACKNOWLEDGEMENTS
J. L. B. L. wishes to thank the anonymous referee for inspiring Section 5, and providing many other valuable suggestions that greatly improved the paper. J. L. B. L. wishes to acknowledge the support of the MIR and MIFR scholarships afforded by the University of Melbourne. This work was supported by resources awarded under Astronomy Australia Ltds merit allocation scheme on the gSTAR national facility at Swinburne University of Technology. gSTAR is funded by Swinburne and the Australian Governments Education Investment Fund. This work was also supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia. The simulations in this work make use of the Murchison Radio-astronomy Observatory, operated by CSIRO. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the operation of the MWA is provided by the Australian Government Department of Industry and Science and Department of Education (National Collaborative Research Infrastructure Strategy: NCRIS), under a contract to Curtin University administered by Astronomy Australia Limited. We acknowledge the iVEC Petabyte Data Store and the Initiative in Innovative Computing and the CUDA Center for Excellence sponsored by NVIDIA at Harvard University. This research was conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020.
A ALGORITHMS
Algorithm 1: Positional selection criteria for all cross-match combinations associated with a base source. Any catalogue with more than one match source is labelled as ‘repeated’. The algorithm accepts a combination if it is either likely, or if the repeated source is within the resolution of the base catalogue. The retained combinations are then investigated through Algorithm 3 and 4. P u can be modified by the user. At all stages, statistics of the matching process are gathered to propagate through to the final matched catalogue.

Algorithm 2: Positional selection criteria for a single source cross-match. If there is only one combination possible, and it has a positional probability over a given threshold, it is accepted without scrutinising the spectral data. This avoids assuming any spectral model. If the match is below P u, all matched sources are checked to be within the resolution of the base catalogue. As there was only one possible match, a high positional probability was expected, so a spectral test is applied. If the residuals ε, χ2 red of a fit to a power law (as detailed in Section 3.3.1) are below a certain threshold χ2 red, u, the source is accepted. At all stages, statistics of the matching process are gathered to propagate through to the final matched catalogue.

B PARAMETER SPACE
As described in Section 3, there are five parameters that the user declares when running PUMA: the resolution, θr; an upper and lower positional probability, P u, P l; two residual fitting metrics, χ2 red, u, εu. In practise, θr is set by the FWHM of the instrument response of the survey, leaving four parameters to be selected by the user. In Figures B1–B3, a range of parameters are run using the mock catalogues created in Section 5. The numbers of each PUMA classification, as well as the median SI value, are then plotted as 2D histograms. For each histogram, the mean is taken over the range of parameters not being plotted. The results of Figures B1–B3 show that all classifications are robust to the choice of both P u and P l with the exception of when P u = 1 or P l = 1., which causes a sharp increase in the number of sources rejected. As intended, as both χ2 red, u and εu increase, the number of accepted sources increases. The choice of these parameters then comes down to the science case of the user, and how important a fit to a power-law model is. The median of the SI distribution is shown to be extremely robust to the choice of parameters.
Algorithm 3: A test for spectral dominance. If one combination has residuals that are at least three times smaller than all other combinations, and is positionally likely whilst all other combinations are unlikely, accept the source. Positional and spectral dominance are required at the same time, to rule out chance alignment of sources with particular flux densities. Otherwise, the combinations are passed on to Algorithm 4. At all stages, statistics of the matching process are gathered to propagate through to the final matched catalogue.

Algorithm 4: A test for source combining. If no one combination passes Algorithm 3, try combing the flux densities from the sources from the same catalogue. If the combined flux densities pass a spectral test, create a new position for the combined source, weighting the RA and Dec of each source by its flux density. If splitting is implemented, pass to Algorithm 5. Otherwise accept the combined source. If the combination of flux densities does not pass, send the combinations to be investigated by eye. At all stages, statistics of the matching process are gathered to propagate through to the final matched catalogue.

Algorithm 5: A test for source splitting. If a source can be combined, but the components to be combined are separated by a distance larger than the user specified d split, the combination is tested for splitting. If more than one catalogue has repeated sources, the Algorithm requires they have the same amount of sources. Each set of repeated sources are then matched by distance to create components. An SED is constructed for each component, and fit to the linear model. If all components pass the spectral test, the cross-match combination is split up in to multiple cross-matched sources.


Figure B1. An exploration of the effects of parameter space for isolated and dominant classifications. The bottom right panel of (a) shows that χ2 red and ε have no effect on the number of dominant sources; this is because dominance is established using a ratio of residuals, rather than a cut-off. (a) isolated cases. (b) dominant cases.

Figure B2. An exploration of the effects of parameter space for multiple and eyeball classifications. (a) multiple cases. (b) eyeball cases.

Figure B3. An exploration of the effects of parameter space for the reject classification and the median of the SI distribution. (a) reject cases. (b) The median SI.

































