Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T07:58:02.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Photospheric Flux Changes and the MHD Approximation

Published online by Cambridge University Press:  25 April 2016

P. R. Wilson
P. R. Wilson*
Affiliation:
Department of Applied Mathematics, University of Sydney
Get access Rights & Permissions [Opens in a new window]

Extract

The rate of change of magnetic flux Ф contained within a closed curve C moving with the plasma velocity u, is given by

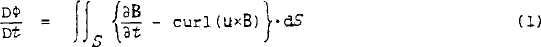
where B is the magnetic induction and S is a surface bounded by the curve C. Using the hydromagnetic equation,

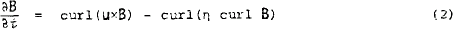
where η is the magnetic diffusivity, this becomes

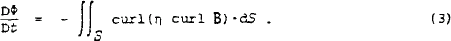
In many astrophysical contexts η is small and thus approximately

Since this implies that the flux within any moving closed curve does not change, the field is said to be ‘frozen into’ the plasma and moving with it.

Type
Contributions
Information
Publications of the Astronomical Society of Australia , Volume 5 , Issue 4 , 1984 , pp. 500 - 502
Copyright
Copyright © Astronomical Society of Australia 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braginskii, S. I., in ‘Reviews of Plasma Physics’, ed. Leontovish, M. A. (Consultants Bureau, New York), 1, p. 205 (1965).Google Scholar
Bumba, V., Bull. Astron. Inst. Czech., 32, 129 (1981).Google Scholar
Cowling, T. G., ‘Magneto-hydrodynamics’, (Interscience, New York), 2nd Edition, (1980).Google Scholar
Harvey, J. W., private communication (1984).Google Scholar
Jones, H., private communication (1984).Google Scholar
Pert, G. J., J. Plasma Phys., 18, 227 (1977).Google Scholar
Simon, G. W., and Wilson, P. R., (in preparation) (1984).Google Scholar
Topka, K., and Tarbell, E., private communication (1983).Google Scholar
Wallenhorst, S. G., and Howard, R., in ‘The Physics of Sunspots’, eds. Cram, L. E. and Thomas, J. H. (Sacramento Peak Observatory, New Mexico), p. 55 (1981).Google Scholar
Wilson, P. R., and Simon, G. W., Astrophys. J., 273, 805 (1983).Google Scholar