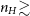1. Introduction
Magnesium is abundant in the solar atmosphere, and its neutral and singly ionized states give rise to numerous spectral lines with significant diagnostic potential in the photosphere, chromosphere, and the transition region. NASA’s Interface Region Imaging Spectrograph (IRIS) spacecraft provided an important opportunity to observe intensity spectra of several lines, including the Mg II lines. Various works have presented forward modelling of the intensity of Mg II lines (e.g. Leenaarts et al. Reference Leenaarts, Pereira, Carlsson, Uitenbroek and De Pontieu2013).
Polarisation spectra of Mg II h-k lines have been observed through the Ultra-Violet Spectro-Polarimeter on board the Solar Maximum Mission (Calvert et al. Reference Calvert, Griner and Montenegro1979, Bohlin et al. Reference Bohlin, Frost, Burr, Guha and Withbroe1980, Woodgate et al. Reference Woodgate, Tandberg-Hanssen and Bruner1980). These measurements have been analysed by Henze & Stenflo (Reference Henze and Stenflo1987). Furthermore, several theoretical studies have improved our comprehension of the physical processes that cause the polarisation of the Mg II h-k lines, highlighting their magnetic sensitivity (e.g. Auer et al. 1980, Henze & Stenflo Reference Henze and Stenflo1987, Belluzzi & Trujillo Bueno Reference Belluzzi and Trujillo Bueno2012; Alsina Ballester et al. Reference Alsina Ballester, Belluzzi and Trujillo Bueno2016; del Pino Alemán et al. Reference del Pino Alemán, Casini and Manso Sainz2016, Reference del Pino Alemán, Trujillo Bueno, Casini and Manso Sainz2020). In addition, UV spectropolarimeter called Chromospheric LAyer SpectroPolarimeter (CLASP2) was launched on 2019 to observe polarized light emitted by Mg II ions around the wavelength of 280 nm for investigating the magnetic properties of the transition region and the upper chromosphere.
Our aim is to contribute to the efforts concentrated on observing and interpreting Mg II lines by elucidating the possible collisional depolarising role during their formation. In fact, collisions with hydrogen might be important for modelling chromospheric Mg II lines and their depolarising effect has not been elucidated in details previously.
We model the Mg II by a multi-level and then by a more realistic multi-term atomic model (see Landi Degl’Innocenti & Landolfi Reference Landi Degl’Innocenti2004). We provide all needed collisional rates due to the Mg II+H collisions. We include these rates in the statistical equilibrium equations (SEE) for multi-level and multi-term atomic models, which are then solved to determine how collisions impact the polarisation of the Mg II lines.
2. Collisional effects in multi-level case
2.1 SEE collisional contribution
We adopt the LS coupling scheme, where the level is usually denoted by
![]() $nl \, ^{2S+1}L_J$
, where n is the principal quantum number, l is the orbital angular momentum quantum number, S is the total spin, L is the total orbital angular momentum, and J is the total angular momentum defined as
$nl \, ^{2S+1}L_J$
, where n is the principal quantum number, l is the orbital angular momentum quantum number, S is the total spin, L is the total orbital angular momentum, and J is the total angular momentum defined as
![]() $J = L + S$
(e.g. Martin & Wiese Reference Martin and Wiese2002). For simplicity, we will also use the notations
$J = L + S$
(e.g. Martin & Wiese Reference Martin and Wiese2002). For simplicity, we will also use the notations
![]() $nl \, ^{2S+1}L_J = nl \, LS\,J = \alpha J$
, where
$nl \, ^{2S+1}L_J = nl \, LS\,J = \alpha J$
, where
![]() $\alpha$
represents the set of quantum numbers
$\alpha$
represents the set of quantum numbers
![]() $(n \, l \, L S)$
. In the context of the polarisation studies, the representation of Mg II states using the atomic density matrix formalism based on irreducible tensorial operators is demonstrated to be the most appropriate (e.g. Sahal-Bréchot Reference Sahal-Bréchot1977; Landi Degl’Innocenti & Landolfi Reference Landi Degl’Innocenti2004). In this basis, the contribution of depolarising isotropic collisions to the SEE is given by (e.g. Sahal-Bréchot et al. Reference Sahal-Bréchot, Derouich, Bommier and Barklem2007):
$(n \, l \, L S)$
. In the context of the polarisation studies, the representation of Mg II states using the atomic density matrix formalism based on irreducible tensorial operators is demonstrated to be the most appropriate (e.g. Sahal-Bréchot Reference Sahal-Bréchot1977; Landi Degl’Innocenti & Landolfi Reference Landi Degl’Innocenti2004). In this basis, the contribution of depolarising isotropic collisions to the SEE is given by (e.g. Sahal-Bréchot et al. Reference Sahal-Bréchot, Derouich, Bommier and Barklem2007):
 \begin{align} \left( \frac{d \; \rho_q^{k} (\alpha \; J)}{dt} \right)_\textrm{coll}= & \ - D^k(\alpha \; J, T) \; \rho_q^{k} (\alpha \; J) \nonumber \\&- \rho_q^{k} (\alpha \; J) \sum_{J^{\prime} \ne J} \sqrt{\frac{2J^{\prime}+1}{2J+1}} D^0 (\alpha \; J \to \alpha \; J^{\prime}, T) \nonumber \\&+ \sum_{J^{\prime} \ne J}D^k(\alpha \; J^{\prime} \to \alpha \; J, T) \; \rho_q^{k} (\alpha \; J^{\prime}) \,, \end{align}
\begin{align} \left( \frac{d \; \rho_q^{k} (\alpha \; J)}{dt} \right)_\textrm{coll}= & \ - D^k(\alpha \; J, T) \; \rho_q^{k} (\alpha \; J) \nonumber \\&- \rho_q^{k} (\alpha \; J) \sum_{J^{\prime} \ne J} \sqrt{\frac{2J^{\prime}+1}{2J+1}} D^0 (\alpha \; J \to \alpha \; J^{\prime}, T) \nonumber \\&+ \sum_{J^{\prime} \ne J}D^k(\alpha \; J^{\prime} \to \alpha \; J, T) \; \rho_q^{k} (\alpha \; J^{\prime}) \,, \end{align}
where k,
![]() $0 \le k \le k_\textrm{max}$
, is the tensorial order with
$0 \le k \le k_\textrm{max}$
, is the tensorial order with
![]() $k_\textrm{max}\!=\! 2J$
for
$k_\textrm{max}\!=\! 2J$
for
![]() $J\!=\!J^{\prime}$
and
$J\!=\!J^{\prime}$
and
![]() $k_\textrm{max}\!=\! min \{2J,2J^{\prime}\}$
for
$k_\textrm{max}\!=\! min \{2J,2J^{\prime}\}$
for
![]() $J \!\ne\! J^{\prime}$
.
$J \!\ne\! J^{\prime}$
.
![]() $D^k(\alpha \; J, T)$
and
$D^k(\alpha \; J, T)$
and
![]() $D^k(\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
are the depolarisation and the polarisation transfer rates, respectively. Note that
$D^k(\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
are the depolarisation and the polarisation transfer rates, respectively. Note that
![]() $D^0 (\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
is the population transfer rate between the levels
$D^0 (\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
is the population transfer rate between the levels
![]() $(\alpha \; J)$
and
$(\alpha \; J)$
and
![]() $(\alpha \;J^{\prime})$
. These rates should be calculated independently to enter the SEE. To model the Mg II ions, we consider a comprehensive atomic model containing large number of lines ranging from the ultraviolet to the infrared as shown in Figure 1 (see also Fig. 1 of Leenaarts et al. Reference Leenaarts, Pereira, Carlsson, Uitenbroek and De Pontieu2013).
$(\alpha \;J^{\prime})$
. These rates should be calculated independently to enter the SEE. To model the Mg II ions, we consider a comprehensive atomic model containing large number of lines ranging from the ultraviolet to the infrared as shown in Figure 1 (see also Fig. 1 of Leenaarts et al. Reference Leenaarts, Pereira, Carlsson, Uitenbroek and De Pontieu2013).

Figure 1. Energy diagram of the atomic model of Mg II adopted for this work. Note that
![]() $p-d$
transitions taken into account are represented in blue,
$p-d$
transitions taken into account are represented in blue,
![]() $s-p$
transitions are represented in grey, and
$s-p$
transitions are represented in grey, and
![]() $f-d$
transitions are represented in brown colour.
$f-d$
transitions are represented in brown colour.
2.2 Collisional rates for P-, D-, and F-states
The atomic model adopted in this paper contains s-, p-, d-, and f-states (see Figure 1). Note that s-states of the present model are not linearly polarisable and, therefore, are not affected by collisions with hydrogen atoms. The rates
![]() $D^k(\alpha \; J, T)$
and
$D^k(\alpha \; J, T)$
and
![]() $D^k(\alpha \; J^{\prime} \!\to\! \alpha \; J, T)$
for the levels of the
$D^k(\alpha \; J^{\prime} \!\to\! \alpha \; J, T)$
for the levels of the
![]() $3p \; ^2P$
term have been previously calculated using the hybrid method developed by Derouich (Reference Derouich2020). In order to obtain the rates associated to the other terms of Figure 1:
$3p \; ^2P$
term have been previously calculated using the hybrid method developed by Derouich (Reference Derouich2020). In order to obtain the rates associated to the other terms of Figure 1:
![]() $4 p \; ^2P$
,
$4 p \; ^2P$
,
![]() $3 d \; ^2D$
,
$3 d \; ^2D$
,
![]() $4 d \; ^2D$
, and
$4 d \; ^2D$
, and
![]() $4 f \; ^2F$
, one can either employ a direct calculation by running the numerical code of collisions for each level as explained in the formalism presented by Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004) or use the genetic programming (GP) functions presented in Derouich (Reference Derouich2017) for p-states, Derouich et al. (Reference Derouich, Basurah and Badruddin2017) for d-states and Derouich (Reference Derouich2018) for f-states.
$4 f \; ^2F$
, one can either employ a direct calculation by running the numerical code of collisions for each level as explained in the formalism presented by Derouich et al. (Reference Derouich, Sahal-Bréchot and Barklem2004) or use the genetic programming (GP) functions presented in Derouich (Reference Derouich2017) for p-states, Derouich et al. (Reference Derouich, Basurah and Badruddin2017) for d-states and Derouich (Reference Derouich2018) for f-states.
Whether running the numerical code of collisions or using the GP functions, it is necessary to determine the Unsöld energy
![]() $E_P$
for each ionic state. This energy must then be used as input for either the numerical code or the GP functions. In addition to
$E_P$
for each ionic state. This energy must then be used as input for either the numerical code or the GP functions. In addition to
![]() $E_P$
, the effective quantum number
$E_P$
, the effective quantum number
![]() $n^*$
is also needed as input parameter. If the energy of the state
$n^*$
is also needed as input parameter. If the energy of the state
![]() $|{a}\rangle $
of the valence electron is
$|{a}\rangle $
of the valence electron is
![]() $E_{a}$
and the ionisation energy of the ion is
$E_{a}$
and the ionisation energy of the ion is
![]() $E_\infty$
, the effective quantum number
$E_\infty$
, the effective quantum number
![]() $n^*$
is given by (see, e.g., Derouich Reference Derouich2004):
$n^*$
is given by (see, e.g., Derouich Reference Derouich2004):
where the energies are in atomic units. Values of
![]() $n^*$
are provided in Table 1 for all the cases where
$n^*$
are provided in Table 1 for all the cases where
![]() $n^*$
is required to determine the collisional rates. Appropriate value of
$n^*$
is required to determine the collisional rates. Appropriate value of
![]() $E_p$
can then be calculated from the Unsöld formula (see, e.g., Barklem & O’Mara Reference Barklem and O’Mara1998):
$E_p$
can then be calculated from the Unsöld formula (see, e.g., Barklem & O’Mara Reference Barklem and O’Mara1998):
Table 1. Mg II atomic and collisional parameters for the multi-level case

Note that the collisional rates as they are presented in this section depend on the precision of the calculation of
![]() $E_p$
, which is related to the precision of
$E_p$
, which is related to the precision of
![]() $C_6$
obtained from the Kurucz methodology and
$C_6$
obtained from the Kurucz methodology and
![]() $ \lt \! r^2 \! \gt $
resulting from the hydrogenic approximation. To examine the dependence of the depolarisation rates.
$ \lt \! r^2 \! \gt $
resulting from the hydrogenic approximation. To examine the dependence of the depolarisation rates.
in atomic units, where
![]() $C_6$
is the van der Waals coefficient (see Table 1), and
$C_6$
is the van der Waals coefficient (see Table 1), and
![]() $ \lt \! r^2 \! \gt $
is the average of the squared distance between the electron of valence and the nucleus of the perturbed ion (see Table 1). By adopting the hydrogenic approximation, one has for singly ionized atoms (see, e.g., Barklem Reference Barklem1998):
$ \lt \! r^2 \! \gt $
is the average of the squared distance between the electron of valence and the nucleus of the perturbed ion (see Table 1). By adopting the hydrogenic approximation, one has for singly ionized atoms (see, e.g., Barklem Reference Barklem1998):
The van der Waals coefficients are available on Kurucz’s website (Kurucz Reference Kurucz2013; kurucz.harvard.edu), namely the file “gammasum1201z.gam” which contains comprehensive information on the Mg II lines and relevant atomic parameters. For the 3 d
![]() $^2D$
state,
$^2D$
state,
Note that the definition of
![]() $C_6$
included in Equation 3 giving
$C_6$
included in Equation 3 giving
![]() $E_p$
differs by a factor of h (h is the Planck constant) from
$E_p$
differs by a factor of h (h is the Planck constant) from
![]() $C^{\textrm{Kurucz}}_6$
, in addition to the difference in units since
$C^{\textrm{Kurucz}}_6$
, in addition to the difference in units since
![]() $C_6$
of Equation 3 is in a.u. while
$C_6$
of Equation 3 is in a.u. while
![]() $C^{\textrm{Kurucz}}_6$
is in
$C^{\textrm{Kurucz}}_6$
is in
![]() $\text{cm}^6 \; \text{s}^{-1}$
. In fact,
$\text{cm}^6 \; \text{s}^{-1}$
. In fact,
implying that:
Similar calculation allows us to obtain all
![]() $E_p$
values needed for the computation of depolarisation and polarisation and population transfer rates (see Table 1).
$E_p$
values needed for the computation of depolarisation and polarisation and population transfer rates (see Table 1).
Our depolarisation and polarisation transfer rates are written in the form
![]() $D^k=a^k \times 10^{-9} \; n_H \left(\! \frac{T}{5000} \!\right)^{\lambda^k}$
. Note that
$D^k=a^k \times 10^{-9} \; n_H \left(\! \frac{T}{5000} \!\right)^{\lambda^k}$
. Note that
![]() $a^k \times 10^{-9}=D^k/n_H$
at
$a^k \times 10^{-9}=D^k/n_H$
at
![]() $T=5000$
K and
$T=5000$
K and
![]() $\lambda^k$
is the so-called velocity exponent (e.g. Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004). Values of
$\lambda^k$
is the so-called velocity exponent (e.g. Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004). Values of
![]() $a^k$
and
$a^k$
and
![]() $\lambda^k$
with even k-order, which are relevant for linear polarisation treatment within the multi-level model, are provided in Table 2 (see Appendix 1). In particular, we provide only
$\lambda^k$
with even k-order, which are relevant for linear polarisation treatment within the multi-level model, are provided in Table 2 (see Appendix 1). In particular, we provide only
![]() $D^k(\alpha \;J \!\to\! \alpha \;J^{\prime})$
since
$D^k(\alpha \;J \!\to\! \alpha \;J^{\prime})$
since
![]() $D^k(\alpha \;J^{\prime} \!\to\! \alpha \;J)$
are calculated by applying the detailed balance relation:
$D^k(\alpha \;J^{\prime} \!\to\! \alpha \;J)$
are calculated by applying the detailed balance relation:
with
![]() $k_B$
is the Boltzmann constant and
$k_B$
is the Boltzmann constant and
![]() $E_{J}$
is the energy of the J-level.
$E_{J}$
is the energy of the J-level.
![]() $D^{2}(3d \; ^2D_{\frac{3}{2}})$
and
$D^{2}(3d \; ^2D_{\frac{3}{2}})$
and
![]() $D^{2}(3d \; ^2D_{\frac{5}{2}}) $
and transfer rates
$D^{2}(3d \; ^2D_{\frac{5}{2}}) $
and transfer rates
![]() $D^{2}(3d \; ^2D_{\frac{3}{2}} \!\to\! 3d \; ^2D_{\frac{5}{2}})$
and
$D^{2}(3d \; ^2D_{\frac{3}{2}} \!\to\! 3d \; ^2D_{\frac{5}{2}})$
and
![]() $D^{0}(3d \; ^2D_{\frac{3}{2}} \!\to\! 3d \; ^2D_{\frac{5}{2}}) $
to
$D^{0}(3d \; ^2D_{\frac{3}{2}} \!\to\! 3d \; ^2D_{\frac{5}{2}}) $
to
![]() $E_p$
, we study the sensitivity of the
$E_p$
, we study the sensitivity of the
![]() $a^k$
coefficients to the
$a^k$
coefficients to the
![]() $E_p$
variation. As it can be seen in Figure 2, the
$E_p$
variation. As it can be seen in Figure 2, the
![]() $a^k$
are sufficiently stable with respect to sensible variation of
$a^k$
are sufficiently stable with respect to sensible variation of
![]() $E_p$
. The range of the calculation presented in Figure 2 is chosen to contain possible values of
$E_p$
. The range of the calculation presented in Figure 2 is chosen to contain possible values of
![]() $E_p$
, based on different models, such as the one adopted by O’Mara & Barklem (Reference Barklem1998) for the
$E_p$
, based on different models, such as the one adopted by O’Mara & Barklem (Reference Barklem1998) for the
![]() $3d \; ^2D$
state of the Ca II, where
$3d \; ^2D$
state of the Ca II, where
![]() $E_p$
was found to be between -0.918 and -1.236 a.u.
$E_p$
was found to be between -0.918 and -1.236 a.u.

Figure 2. Variation of the collisional rates with
![]() $E_p$
.
$E_p$
.
2.3 Resolution of the SEE in the multi-level case
We consider a slab of Mg II ions positioned at the solar atmosphere, and we assume a zero-magnetic field case. To generate a polarized light, the slab of Mg II ions is assumed to be illuminated from below by anisotropic solar radiation. The components of the incoming radiation field are typically represented by
![]() $J_{q}^{k} $
, where k is the tensorial order and q signifies the coherences in the tensorial basis (
$J_{q}^{k} $
, where k is the tensorial order and q signifies the coherences in the tensorial basis (
![]() $-k \le q \le k$
). The atmospheric light is considered to be uniform and exhibits cylindrical symmetry about the local solar vertical at the scattering center (the Mg II ion) which implies that, for a given frequency
$-k \le q \le k$
). The atmospheric light is considered to be uniform and exhibits cylindrical symmetry about the local solar vertical at the scattering center (the Mg II ion) which implies that, for a given frequency
![]() $\nu$
, only
$\nu$
, only
![]() $J^0_0(\nu)$
and
$J^0_0(\nu)$
and
![]() $J^2_0(\nu)$
are non-zero. The components
$J^2_0(\nu)$
are non-zero. The components
![]() $J^0_0(\nu)$
and
$J^0_0(\nu)$
and
![]() $J^2_0(\nu)$
are given by the number of photons per mode
$J^2_0(\nu)$
are given by the number of photons per mode
![]() $\bar{n}(\nu) = J^0_0 \; (c^2/2hJ^0_0(\nu)^3)$
and the value of the anisotropy factor
$\bar{n}(\nu) = J^0_0 \; (c^2/2hJ^0_0(\nu)^3)$
and the value of the anisotropy factor
![]() $w(\nu) = \sqrt{2} \; (J^2_0/J^0_0)$
(see e.g. Derouich et al. Reference Derouich, Trujillo Bueno and Manso Sainz2007). Calculations of the non-zero components of the incident radiation field,
$w(\nu) = \sqrt{2} \; (J^2_0/J^0_0)$
(see e.g. Derouich et al. Reference Derouich, Trujillo Bueno and Manso Sainz2007). Calculations of the non-zero components of the incident radiation field,
![]() $J^0_0(\nu)$
and
$J^0_0(\nu)$
and
![]() $J^2_0(\nu)$
, for each line are based on Cox (Reference Cox2000) (see also Allen & Cox Reference Allen and Cox1999, Thuillier et al. Reference Thuillier, Floyd and Woods2004).
$J^2_0(\nu)$
, for each line are based on Cox (Reference Cox2000) (see also Allen & Cox Reference Allen and Cox1999, Thuillier et al. Reference Thuillier, Floyd and Woods2004).
The anisotropic incident radiation field induces population imbalances and coherences between the Zeeman sublevels of a given
![]() $(\alpha J)$
-level of the Mg II ions. These population imbalances and coherences are referred to as atomic polarisation. Under these conditions, owing to the cylindrical symmetry of the problem, only linear polarisation is produced by scattering, and only the density matrix elements with
$(\alpha J)$
-level of the Mg II ions. These population imbalances and coherences are referred to as atomic polarisation. Under these conditions, owing to the cylindrical symmetry of the problem, only linear polarisation is produced by scattering, and only the density matrix elements with
![]() $q=0$
and k even are non-zero. The statistical equilibrium equations (SEE) include 26 unknowns, corresponding to the density matrix elements
$q=0$
and k even are non-zero. The statistical equilibrium equations (SEE) include 26 unknowns, corresponding to the density matrix elements
![]() $ \rho_0^{k}$
.
$ \rho_0^{k}$
.
The Einstein coefficients required for the radiative rates entering the SEE are extracted from NIST database. In addition to the expressions of the radiative rates, which are taken from Landi Degl’Innocenti & Landolfi (Reference Landi Degl’Innocenti2004), the numerical code incorporates the collisional rates, given in Table 2, as input to compute the values of the atomic density matrix elements. These values are affected by the gain terms called collisional polarisation transfer rates and denoted by
![]() $D^k(\alpha \; J^{\prime} \!\to\! \alpha \; J)$
, and by the loss (collisional relaxation) terms
$D^k(\alpha \; J^{\prime} \!\to\! \alpha \; J)$
, and by the loss (collisional relaxation) terms
![]() $D^k(\alpha \; J)+\sqrt{\frac{2J^{\prime}+1}{2J+1}} D^0 (\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
(see Equation (1)).
$D^k(\alpha \; J)+\sqrt{\frac{2J^{\prime}+1}{2J+1}} D^0 (\alpha \; J \!\to\! \alpha \; J^{\prime}, T)$
(see Equation (1)).
Our focus is on the effects of elastic collisions with neutral hydrogen to complement existing studies that omit these collisions. While a more comprehensive analysis of Mg II line polarisation would include processes such as collisions with electrons and polarized radiative transfer in a magnetized atmosphere; these are beyond the scope of this paper.
Given that collisional rates are proportional to the hydrogen density
![]() $n_H$
(according to the impact approximation), analyzing how polarisation depends on collisional rates is equivalent to examining its dependence on
$n_H$
(according to the impact approximation), analyzing how polarisation depends on collisional rates is equivalent to examining its dependence on
![]() $n_H$
. In theory, even if the core of a line is formed at higher chromospheric layers, its wings can be formed in deeper layers of the chromosphere. Given that the density of hydrogen atoms
$n_H$
. In theory, even if the core of a line is formed at higher chromospheric layers, its wings can be formed in deeper layers of the chromosphere. Given that the density of hydrogen atoms
![]() $n_H$
is larger in deep chromospheric layers and that the considered lines cover spectral window from the ultraviolet to the infrared, one should perform a scan over large range of
$n_H$
is larger in deep chromospheric layers and that the considered lines cover spectral window from the ultraviolet to the infrared, one should perform a scan over large range of
![]() $n_H$
values. We solve the SEE to calculate the non-zero
$n_H$
values. We solve the SEE to calculate the non-zero
![]() $ \rho_0^{k}$
elements by adopting the multi-level atomic model presented in the Figure 1 for a wide range of hydrogen density values
$ \rho_0^{k}$
elements by adopting the multi-level atomic model presented in the Figure 1 for a wide range of hydrogen density values
![]() $n_H$
going from
$n_H$
going from
![]() $10^{12}$
cm
$10^{12}$
cm
![]() $^{-3}$
to
$^{-3}$
to
![]() $10^{19}$
cm
$10^{19}$
cm
![]() $^{-3}$
while adopting a solar temperature
$^{-3}$
while adopting a solar temperature
![]() $T=$
5000 K. We point out the range of
$T=$
5000 K. We point out the range of
![]() $n_H$
where the effect of collisions is important.
$n_H$
where the effect of collisions is important.
In Figure 3, we shows the ratio
![]() $\frac{\rho_0^{k=2}(n_H)}{\rho_0^{k=2}(n_H=0)}$
giving the variation of the alignment as a function of
$\frac{\rho_0^{k=2}(n_H)}{\rho_0^{k=2}(n_H=0)}$
giving the variation of the alignment as a function of
![]() $n_H$
. It can be seen that collisions start influencing the alignment of the
$n_H$
. It can be seen that collisions start influencing the alignment of the
![]() $4p \; ^2P_{3/2}$
level for
$4p \; ^2P_{3/2}$
level for
![]() $n_H$
$n_H$
![]() $\sim$
$\sim$
![]() $10^{14}$
cm
$10^{14}$
cm
![]() $^{-3}$
. Consequently, the 6 lines directly connected to this level (see Figure 1) should be affected by collisions for
$^{-3}$
. Consequently, the 6 lines directly connected to this level (see Figure 1) should be affected by collisions for
![]() $n_H$
$n_H$
![]() $\gtrsim$
$\gtrsim$
![]() $10^{14}$
cm
$10^{14}$
cm
![]() $^{-3}$
. Lines with upper and/or lower levels different from the 4p
$^{-3}$
. Lines with upper and/or lower levels different from the 4p
![]() $^2P_{3/2}$
could be also indirectly slightly affected for
$^2P_{3/2}$
could be also indirectly slightly affected for
![]() $n_H$
$n_H$
![]() $\gtrsim$
$\gtrsim$
![]() $10^{14}$
cm
$10^{14}$
cm
![]() $^{-3}$
due to the coupling between the different levels through the SEE. All the levels other than
$^{-3}$
due to the coupling between the different levels through the SEE. All the levels other than
![]() $4p \; ^2P_{3/2}$
start to be depolarized for
$4p \; ^2P_{3/2}$
start to be depolarized for
![]() $n_H$
$n_H$
![]() $\gtrsim$
$\gtrsim$
![]() $10^{15}$
cm
$10^{15}$
cm
![]() $^{-3}$
.
$^{-3}$
.

Figure 3. Variation of the ratio
![]() $\frac{\rho_0^{2}(n_H)}{\rho_0^{2}(n_H=0)} $
as a function of
$\frac{\rho_0^{2}(n_H)}{\rho_0^{2}(n_H=0)} $
as a function of
![]() $n_H$
for the Mg II levels within the framework of the multi-level model.
$n_H$
for the Mg II levels within the framework of the multi-level model.
3. Multi-term case
In this section, we will allow for coherences between different
![]() $(\alpha J)$
and
$(\alpha J)$
and
![]() $(\alpha J^{\prime})$
-levels grouped within the same term
$(\alpha J^{\prime})$
-levels grouped within the same term
![]() $n\, l \, ^{2S+1}L$
. The density matrix elements associated to these coherences are denoted by
$n\, l \, ^{2S+1}L$
. The density matrix elements associated to these coherences are denoted by
![]() $\rho_q^{k} (\alpha \; JJ^{\prime})$
. This is the so-called mutli-term case (see Section 7.5 of Landi Degl’Innocenti & Landolfi Reference Landi Degl’Innocenti2004). Indeed, a more realistic diagnostic of the polarisation of the lines of Mg II should be performed in the framework of the multi-term atomic model due to the tiny energy separation between the levels of the d- terms and similarly between those of the f-terms. We consider the atomic model of Mg II shown in Figure 1, with eight terms: 3 s
$\rho_q^{k} (\alpha \; JJ^{\prime})$
. This is the so-called mutli-term case (see Section 7.5 of Landi Degl’Innocenti & Landolfi Reference Landi Degl’Innocenti2004). Indeed, a more realistic diagnostic of the polarisation of the lines of Mg II should be performed in the framework of the multi-term atomic model due to the tiny energy separation between the levels of the d- terms and similarly between those of the f-terms. We consider the atomic model of Mg II shown in Figure 1, with eight terms: 3 s
![]() $^2S$
, 3 p
$^2S$
, 3 p
![]() $^2P$
, 4 s
$^2P$
, 4 s
![]() $^2S$
, 3 d
$^2S$
, 3 d
![]() $^2D$
, 4 p
$^2D$
, 4 p
![]() $^2P$
, 5 s
$^2P$
, 5 s
![]() $^2S$
, 3 d
$^2S$
, 3 d
![]() $^2D$
and 4 f
$^2D$
and 4 f
![]() $^2F$
; we take into account coherences between different J-levels within these terms. In fact, In the spherical statistical tensors representation, the contribution of the isotropic collisions to the SEE in the multi-term case is:
$^2F$
; we take into account coherences between different J-levels within these terms. In fact, In the spherical statistical tensors representation, the contribution of the isotropic collisions to the SEE in the multi-term case is:
 \begin{align} \left(\! \frac{d \; \rho_q^{k} (\alpha \; JJ^{\prime})}{dt} \!\right)_\textrm{coll} = & \; - \left[\! \sum_{(J^{\prime\prime}J^{\prime\prime\prime})\ne (JJ^{\prime})} \!\! \sqrt{ \frac{J^{\prime\prime}+J^{\prime\prime\prime}+1} {J+J^{\prime}+1}} \; D^0(\alpha \; JJ^{\prime} \!\to\! \alpha \; J^{\prime\prime}J^{\prime\prime\prime}) \right.\nonumber \\&+ \left. D^k(\alpha \; JJ^{\prime}) \right] \times \rho_q^{k} (\alpha \; JJ^{\prime}) \\&+\! \sum_{(J^{\prime\prime}J^{\prime\prime\prime})\ne (JJ^{\prime})} \!\!\!\! D^k(\alpha \; J^{\prime\prime}J^{\prime\prime\prime} \!\to\! \alpha \; JJ^{\prime}) \times \rho_q^{k} (\alpha \; J^{\prime\prime}J^{\prime\prime\prime}) \nonumber\end{align}
\begin{align} \left(\! \frac{d \; \rho_q^{k} (\alpha \; JJ^{\prime})}{dt} \!\right)_\textrm{coll} = & \; - \left[\! \sum_{(J^{\prime\prime}J^{\prime\prime\prime})\ne (JJ^{\prime})} \!\! \sqrt{ \frac{J^{\prime\prime}+J^{\prime\prime\prime}+1} {J+J^{\prime}+1}} \; D^0(\alpha \; JJ^{\prime} \!\to\! \alpha \; J^{\prime\prime}J^{\prime\prime\prime}) \right.\nonumber \\&+ \left. D^k(\alpha \; JJ^{\prime}) \right] \times \rho_q^{k} (\alpha \; JJ^{\prime}) \\&+\! \sum_{(J^{\prime\prime}J^{\prime\prime\prime})\ne (JJ^{\prime})} \!\!\!\! D^k(\alpha \; J^{\prime\prime}J^{\prime\prime\prime} \!\to\! \alpha \; JJ^{\prime}) \times \rho_q^{k} (\alpha \; J^{\prime\prime}J^{\prime\prime\prime}) \nonumber\end{align}
Note that J,
![]() $J^{\prime}$
,
$J^{\prime}$
,
![]() $J^{\prime\prime}$
, and
$J^{\prime\prime}$
, and
![]() $J^{\prime\prime\prime}$
represent possible values of the total angular momentum within the same term
$J^{\prime\prime\prime}$
represent possible values of the total angular momentum within the same term
![]() $n\, l \, ^{2S+1}L$
.
$n\, l \, ^{2S+1}L$
.
The radiative contributions are taken from multi-term atomic model as described by Landi Degl’Innocenti & Landolfi (Reference Landi Degl’Innocenti2004). In order to calculate
![]() $\rho_q^{k} (\alpha \, JJ^{\prime})$
, we need the depolarisation rates
$\rho_q^{k} (\alpha \, JJ^{\prime})$
, we need the depolarisation rates
![]() $D^k(\alpha \,JJ^{\prime})$
and the polarisation/population transfer rates
$D^k(\alpha \,JJ^{\prime})$
and the polarisation/population transfer rates
![]() $D^k(\alpha \,JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})$
with
$D^k(\alpha \,JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})$
with
![]() $(JJ^{\prime}) \ne (J^{\prime\prime}J^{\prime\prime\prime})$
due to collisions of H atoms in their ground state
$(JJ^{\prime}) \ne (J^{\prime\prime}J^{\prime\prime\prime})$
due to collisions of H atoms in their ground state
![]() $^2S_{1/2}$
with Mg II presented by the eight-term atomic model adopted in this work. Direct calculation of the
$^2S_{1/2}$
with Mg II presented by the eight-term atomic model adopted in this work. Direct calculation of the
![]() $D^k(\alpha \, JJ^{\prime})$
and
$D^k(\alpha \, JJ^{\prime})$
and
![]() $D^k(\alpha \, JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})$
rates is a complicated task since one should take into account the coherences between J-levels when calculating the interaction potential and solving the Schrödinger equation. At the best of our knowledge, this direct calculation have not been performed neither theoretically nor experimentally. To address this problem, one can adopt an indirect and more practical method, based on the frozen spin S approximation. Using this approach, one can show that:
$D^k(\alpha \, JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})$
rates is a complicated task since one should take into account the coherences between J-levels when calculating the interaction potential and solving the Schrödinger equation. At the best of our knowledge, this direct calculation have not been performed neither theoretically nor experimentally. To address this problem, one can adopt an indirect and more practical method, based on the frozen spin S approximation. Using this approach, one can show that:
 \begin{align}D^{k} (\alpha \, JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})=& \sqrt{(2J + 1) (2J^{\prime} + 1) (2J^{\prime\prime} + 1) (2J^{\prime\prime\prime} + 1)} \nonumber \\& \times\sum_{k_L} (2k_L + 1) \, D^{k_L} (n \, l \, L) \\& \times\sum_{k_S}(2k_S + 1) \left \{\!\!\begin{array} {c@{\quad}c@{\quad}c} L & S & J \\ L & S & J^{\prime} \\ k_L & k_S & k\end{array}\!\!\right\}\!\!\left \{\!\!\begin{array} {c@{\quad}c@{\quad}c} L & S & J^{\prime\prime} \\ L & S & J^{\prime\prime\prime} \\ k_L & k_S & k\end{array}\!\!\right\} \nonumber\end{align}
\begin{align}D^{k} (\alpha \, JJ^{\prime} \!\to\! \alpha \, J^{\prime\prime}J^{\prime\prime\prime})=& \sqrt{(2J + 1) (2J^{\prime} + 1) (2J^{\prime\prime} + 1) (2J^{\prime\prime\prime} + 1)} \nonumber \\& \times\sum_{k_L} (2k_L + 1) \, D^{k_L} (n \, l \, L) \\& \times\sum_{k_S}(2k_S + 1) \left \{\!\!\begin{array} {c@{\quad}c@{\quad}c} L & S & J \\ L & S & J^{\prime} \\ k_L & k_S & k\end{array}\!\!\right\}\!\!\left \{\!\!\begin{array} {c@{\quad}c@{\quad}c} L & S & J^{\prime\prime} \\ L & S & J^{\prime\prime\prime} \\ k_L & k_S & k\end{array}\!\!\right\} \nonumber\end{align}
Equation (10) is obtained through a methodology which is formally similar to that firstly proposed by Nienhuis (Reference Nienhuis1976) and Omont (Reference Omont1977) (see also Derouich & Barklem 2007 and Sahal-Bréchot et al. Reference Sahal-Bréchot, Derouich, Bommier and Barklem2007). We note that diagonal rates
![]() $J=J^{\prime}$
and
$J=J^{\prime}$
and
![]() $J^{\prime\prime}=J^{\prime\prime\prime}$
are similar to the transfer rates used for the case of multi-level atomic models. However, calculation of the off-diagonal rates (i.e.
$J^{\prime\prime}=J^{\prime\prime\prime}$
are similar to the transfer rates used for the case of multi-level atomic models. However, calculation of the off-diagonal rates (i.e.
![]() $J \ne J^{\prime}$
and/or
$J \ne J^{\prime}$
and/or
![]() $J^{\prime\prime} \ne J^{\prime\prime\prime}$
) requires the evaluation of the tensorial rates
$J^{\prime\prime} \ne J^{\prime\prime\prime}$
) requires the evaluation of the tensorial rates
![]() $D^{k_L} (n\, l \,L)$
(see Equation (10)). Since the Mg II is a simple ion modelled as a single valence electron outside a spherical ionic core, one has
$D^{k_L} (n\, l \,L)$
(see Equation (10)). Since the Mg II is a simple ion modelled as a single valence electron outside a spherical ionic core, one has
![]() $D^{k_L} (n\, l \,L)=D^{k_l} (n\, l)$
where
$D^{k_L} (n\, l \,L)=D^{k_l} (n\, l)$
where
![]() $L=l$
is the angular momentum of the optical electron (see Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2005 and Sahal-Bréchot et al. Reference Sahal-Bréchot, Derouich, Bommier and Barklem2007).
$L=l$
is the angular momentum of the optical electron (see Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2005 and Sahal-Bréchot et al. Reference Sahal-Bréchot, Derouich, Bommier and Barklem2007).
The main step to obtain
![]() $D^{k_l} (n\, l)$
, needed in Equation (10), is the calculation of the scattering matrix. We ran our numerical code to solve the coupled differential equations and obtain the scattering matrix elements in the basis
$D^{k_l} (n\, l)$
, needed in Equation (10), is the calculation of the scattering matrix. We ran our numerical code to solve the coupled differential equations and obtain the scattering matrix elements in the basis
![]() $|{l m_{l}}\rangle$
for a given velocity and impact parameter b (where
$|{l m_{l}}\rangle$
for a given velocity and impact parameter b (where
![]() $ m_{l}$
is the projection of l along the quantization axis; see Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003a,b; Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004). We then obtained the
$ m_{l}$
is the projection of l along the quantization axis; see Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003a,b; Derouich et al. Reference Derouich, Sahal-Bréchot and Barklem2004). We then obtained the
![]() $D^{k_l} (n\, l)$
rates through an integration over the impact parameter b and the Maxwell distribution of velocities (see Equations 7, 9, 12, and 20 of Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003a).
$D^{k_l} (n\, l)$
rates through an integration over the impact parameter b and the Maxwell distribution of velocities (see Equations 7, 9, 12, and 20 of Derouich et al. Reference Derouich, Sahal-Bréchot, Barklem and O’Mara2003a).
All the non-zero depolarization and polarization transfer rates are written in the form
and are tabulated in the Tables 3, 4, 5, and 6. Note that, in particular,
![]() $ D^{k} (\alpha \, JJ \!\to\! \alpha \, J^{\prime}J^{\prime})= D^{k} (\alpha \, J \!\to\! \alpha \, J^{\prime})$
are related to
$ D^{k} (\alpha \, JJ \!\to\! \alpha \, J^{\prime}J^{\prime})= D^{k} (\alpha \, J \!\to\! \alpha \, J^{\prime})$
are related to
![]() $ D^{k} (\alpha \, J^{\prime}J^{\prime} \!\to\! \alpha \, JJ) $
through the usual detailed balance relation (see Equation (8)). We compute all the non-zero density matrix elements with even k-order which are 44 in the case of our multi-term atomic model of Figure 1. The results obtained for some diagonal elements
$ D^{k} (\alpha \, J^{\prime}J^{\prime} \!\to\! \alpha \, JJ) $
through the usual detailed balance relation (see Equation (8)). We compute all the non-zero density matrix elements with even k-order which are 44 in the case of our multi-term atomic model of Figure 1. The results obtained for some diagonal elements
![]() $\rho_q^{k=2} (\alpha JJ)$
are presented in Figure 4. By comparing with Figure 3, one can see that effects of collisions in the multi-level and multi-term cases have the same behaviours. However, for some cases presented in the Figure 5, the effect of collisions in the multi-term case is quantitatively different from that in the multi-level case. In particular, the levels 4 p
$\rho_q^{k=2} (\alpha JJ)$
are presented in Figure 4. By comparing with Figure 3, one can see that effects of collisions in the multi-level and multi-term cases have the same behaviours. However, for some cases presented in the Figure 5, the effect of collisions in the multi-term case is quantitatively different from that in the multi-level case. In particular, the levels 4 p
![]() $^2P_{3/2}$
, 3 d
$^2P_{3/2}$
, 3 d
![]() $^2D_{3/2}$
, and 4 d
$^2D_{3/2}$
, and 4 d
![]() $^2D_{3/2}$
are more sensitive to collisions in the multi-term case compared to the case of multi-level model. On the other hand, the levels 3d
$^2D_{3/2}$
are more sensitive to collisions in the multi-term case compared to the case of multi-level model. On the other hand, the levels 3d
![]() $^2D_{5/2}$
and 4d
$^2D_{5/2}$
and 4d
![]() $^2D_{5/2}$
are less sensitive to collisions in the multi-term case.
$^2D_{5/2}$
are less sensitive to collisions in the multi-term case.

Figure 4. Same as Figure 3 but for the multi-term model.

Figure 5. Comparison of the ratio
![]() $\frac{\rho_0^{2}(n_H)}{\rho_0^{2}(n_H=0)}$
as a function of
$\frac{\rho_0^{2}(n_H)}{\rho_0^{2}(n_H=0)}$
as a function of
![]() $n_H$
for the multi-term and multi-level cases. The dashed line represents the multi-term case, while the solid line represents the multi-level case.
$n_H$
for the multi-term and multi-level cases. The dashed line represents the multi-term case, while the solid line represents the multi-level case.
As shown above there are some differences in the sensitivity of Mg II levels to collisions with hydrogen atoms between the multi-term and multi-level cases; nevertheless, these differences are practically rather small, specially for sufficiently low
![]() $n_H$
. For the case of the well-known chromospheric Mg II UV h-k lines which are directly connected to the terms 3 s
$n_H$
. For the case of the well-known chromospheric Mg II UV h-k lines which are directly connected to the terms 3 s
![]() $^2S$
and 3 p
$^2S$
and 3 p
![]() $^2P$
, we find that collisions are not important and can be safely neglected in future studies. In fact, the term 3 s
$^2P$
, we find that collisions are not important and can be safely neglected in future studies. In fact, the term 3 s
![]() $^2S$
is not sensitive to collisions with hydrogen atoms because of its total angular momentum being
$^2S$
is not sensitive to collisions with hydrogen atoms because of its total angular momentum being
![]() $1/2$
, meaning the depolarising rates
$1/2$
, meaning the depolarising rates
![]() $D^{k=2}$
are zero by definition. Additionally, for the s-term there is no collisional transfer within the term since it only has one fine structure level. Moreover, the 3 p
$D^{k=2}$
are zero by definition. Additionally, for the s-term there is no collisional transfer within the term since it only has one fine structure level. Moreover, the 3 p
![]() $^2P$
, as it is shown in Figures 3 and 4, it starts to be sensitive to collisions only for
$^2P$
, as it is shown in Figures 3 and 4, it starts to be sensitive to collisions only for
![]() $n_H \!\gtrsim\! 10^{16}$
cm
$n_H \!\gtrsim\! 10^{16}$
cm
![]() $^{-3}$
, which is higher than the typical densities encountered in the chromosphere.
$^{-3}$
, which is higher than the typical densities encountered in the chromosphere.
4. Conclusion
The role of the collisional processes for the Mg II lines is usually disregarded when solving the master equation for the atomic density matrix. We find that the polarization of Mg II h and k lines are not affected by collisions with neutral hydrogen. Nevertheless, we find that collisions with hydrogen atoms are important for other Mg II lines, specially those directly connected to the level 4 p
![]() $^2P_{3/2}$
. Our result could help eliminate potential sources of error or uncertainty and provide clarity on the true significance of collisions for future studies. We provide all the collisional rates for the multi-level (13 levels) and multi-term (8 terms) models of Mg II in Appendix 1 of this paper.
$^2P_{3/2}$
. Our result could help eliminate potential sources of error or uncertainty and provide clarity on the true significance of collisions for future studies. We provide all the collisional rates for the multi-level (13 levels) and multi-term (8 terms) models of Mg II in Appendix 1 of this paper.
Acknowledgements
This research work was funded by Institutional Fund Projects under grant no. (IFPIP:995-130-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia
Data availability statement
Not applicable.
Appendix 1. Collisional data
Table 2. Mg II collisional rates for the multi-level case.

Table 3. P-states: Mg II collisional rates for the multi-term case.

Table 4. 3d
![]() $^2D$
term: Mg II collisional rates for the multi-term case.
$^2D$
term: Mg II collisional rates for the multi-term case.

Table 5. 4d
![]() $^2D$
term: Mg II collisional rates for the multi-term case.
$^2D$
term: Mg II collisional rates for the multi-term case.

Table 6. 4f
![]() $^2F$
term: Mg II collisional rates for the multi-term case.
$^2F$
term: Mg II collisional rates for the multi-term case.