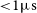1. Introduction
Millisecond pulsars (MSPs) are the sub-population of pulsars that are characterised by short spin periods (
$P<50\,\mathrm{ms}$
) and low magnetic field strengths (
$B_\textrm{surf} <10^{10}\,\mathrm{G}$
).Footnote a The first binary pulsar, PSR B1913
$+$
16 (
$\mathrm{J}1915+1606$
; Hulse & Taylor Reference Hulse and Taylor1975), possessed an unusually low spin period (
$P=59\,\mathrm{ms}$
) and magnetic field strength (
$B_\textrm{surf} = 2 \times 10^{10}\,\mathrm{G}$
) compared to the bulk of the population known at the time, which, apart from the young Crab and Vela pulsars, consisted mainly of solitary pulsars with spin periods of typically 0.1–2 s and magnetic fields of order
$10^{12}\,\mathrm{G}$
. Prior to the discovery of PSR B1913+16, Bisnovatyi-Kogan & Komberg (Reference Bisnovatyi-Kogan and Komberg1974) had predicted that mass accretion onto neutron stars (NSs) may decrease their magnetic fields, and PSR B1913+16 appeared to agree with their prediction as at least one of the NSs in this system must have accreted matter during a previous stage of mass transfer. When the first MSP, PSR B1937+21 (J1939+2134), was discovered with
$P=1.56\,\mathrm{ms}$
and
$B_\textrm{surf}=4\times10^{8}\,\mathrm{G}$
(Backer et al. Reference Backer, Kulkarni, Heiles, Davis and Goss1982), it was soon proposed that a (now missing) companion had been responsible for its spin-up and the low field made spin-up to its millisecond period possible (Alpar et al. Reference Alpar, Cheng, Ruderman and Shaham1982; Radhakrishnan & Srinivasan Reference Radhakrishnan and Srinivasan1982). As more recycled pulsars were discovered, a self-consistent model began to emerge (e.g., Bailes Reference Bailes1989) in which most pulsars lost their binary companions in the initial explosion due to impulsive kicks and mass loss at the time of the first explosion, but those that remained bound had a chance for a second life upon accreting material from their evolved companions that not only reduced their magnetic field strengths but made it possible for them to be spun-up to millisecond periods. NSs with lower-mass companions accrete material for longer than those with high-mass companions because their evolutionary timescales are longer, and they are able to be spun up to very short periods (
$P\sim1.5\,\mathrm{ms}$
) with an associated reduction of their magnetic fields to
${\sim} 10^8\,\mathrm{G}$
. MSPs with heavier white dwarf companions tend to spin more slowly (
$P\sim 10$
–16 ms) with some notable exceptions, such as PSR
$\mathrm{J}1614-2230$
(Crawford et al. Reference Crawford, Roberts, Hessels, Ransom, Livingstone, Tam and Kaspi2006; Demorest et al. Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010), and those with NS companions slower still (
$P\sim 16$
–60 ms). For an early paper describing these models, see Bhattacharya & van den Heuvel (Reference Bhattacharya and van den Heuvel1991), and, for a more recent discussion of their binary properties, Tauris et al. (Reference Tauris2017). Support for these models (see, e.g., Phinney Reference Phinney1992) comes in part from the large fraction of MSPs observed to have binary companions compared to the fraction of ‘normal’ pulsars in binaries (
${\sim} 74\%$
of MSPs are in binaries but only
${\sim}2 \%$
of longer-period pulsars are in binaries; from the Australia Telescope National Facility (ATNF) Pulsar Catalogue, v.1.64, Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005).
Studies of the properties of MSPs and the Galactic MSP population overall have often been limited or biased by small sample sizes (e.g., Johnston & Bailes Reference Johnston and Bailes1991) or by instrumentation that prohibits studies of the polarisation or novel features of the pulse profile, which are probably determined by the pulsar’s magnetosphere and spin period. See, for example, Kramer et al. (Reference Kramer, Xilouris, Lorimer, Doroshenko, Jessner, Wielebinski, Wolszczan and Camilo1998), Xilouris et al. (Reference Xilouris, Kramer, Jessner, von Hoensbroech, Lorimer, Wielebinski, Wolszczan and Camilo1998), and Kramer et al. (Reference Kramer, Lange, Lorimer, Backer, Xilouris, Jessner and Wielebinski1999) for a comprehensive study of 27 MSPs, or the review by Kramer & Xilouris (Reference Kramer, Xilouris, Kramer, Wex and Wielebinski2000), and references therein. The majority of MSPs have been discovered by quasi-uniform surveys by large-aperture telescopes such as the Parkes 64-m radio telescope (also known as Murriyang; e.g., Manchester et al. Reference Manchester2001; Keith et al. Reference Keith2010), the Arecibo 305-m dish (e.g., Cordes et al. Reference Cordes2006), and the Green Bank 100-m Telescope (GBT; e.g., Boyles et al. Reference Boyles2013; Stovall et al. Reference Stovall2014). More recently, other instruments like the Low-Frequency Array (LOFAR) and Giant Metrewave Radio Telescope (GMRT) have discovered pulsars in a combination of quasi-uniform surveys and targeted observations of gamma-ray point sources with pulsar characteristics (see, e.g., Ray et al. Reference Ray2012; Bhattacharyya et al. Reference Bhattacharyya2016; Sanidas et al. Reference Sanidas2019). In many cases, the only published pulse profiles are those formed using survey data and thus limited in resolution due to survey data rates as well as the use of incoherent dispersion correction. It is not uncommon for pulsars with large dispersion measures (DMs) to have narrow features smeared beyond recognition using the discovery hardware which cannot a priori know the DM of the pulsars.
There is also some inconsistency in reported MSP flux densities in the ATNF Pulsar Catalogue and the literature. This is for a variety of reasons that include uncertainties in the pulsar position within the primary beam during initial timing, pulsar scintillation that makes pulsars more likely to have been brighter in their discovery observations, and design limitations that make absolute flux calibration a secondary consideration in the construction of some pulsar survey hardware. For example, the flux density of PSR J1843
$-$
1113 was first determined by Hobbs et al. (Reference Hobbs2004) to be
$S_{1400} = 0.1\,\mathrm{mJy}$
, but was revised to 0.3 mJy by Levin et al. (Reference Levin2013), and then to 0.6 mJy by Desvignes et al. (Reference Desvignes2016).
Analyses of MSP polarisation profiles and their evolution with radio frequency, which could potentially lead to a more consistent theory of the pulsar emission mechanism, have only been performed on samples of a few to
${\sim} 20$
MSPs (e.g., Rankin et al. Reference Rankin2017, and references therein), and the field could significantly benefit from a large comprehensive analysis derived from high signal-to-noise ratio (S/N) observations. Additional areas of pulsar astronomy that would benefit from such a dataset include probing the Galactic magnetic field with rotation measure (RM) measurements (e.g., Han et al. Reference Han, Manchester, van Straten and Demorest2018; Sobey et al. Reference Sobey2019), improving Galactic electron density models with new independent distance measurements (see, e.g., Matthews et al. Reference Matthews2016; Yao, Manchester, & Wang Reference Yao, Manchester and Wang2017), and constraining models of the NS equation of state through MSP mass measurements (Özel & Freire Reference Özel and Freire2016).
Estimates of the total MSP (Levin et al. Reference Levin2013) and binary NS-NS populations (e.g., Burgay et al. Reference Burgay2003) rely upon our understanding of the luminosity function, which in turn depends upon measured MSP distances, flux densities and their pulse shapes. Hence an authoritative survey of MSPs with the same flux density scale, coherent dedispersion to ascertain the true pulse shape, and ultimately pulsar parallaxes from timing is very valuable when we want to estimate their underlying populations and ascertain potential yields for future pulsar surveys and timing programmes such as those planned for the Square Kilometre Array (SKA; e.g., Levin et al. Reference Levin2018).
The new precursor to the SKA in South Africa, MeerKAT (Meer Karoo Array Telescope), presents an opportunity to revisit the fluxes, spectral indices, pulse shapes, polarimetry, and timing potential of the MSPs visible to it. The MeerTime project (Bailes et al. Reference Bailes2020) is a MeerKAT Large Survey Project and has four major themes. These include the Thousand Pulsar Array (Johnston et al. Reference Johnston2020), the Relativistic Binary programme (Kramer et al. Reference Kramer2021), the Globular Cluster pulsar timing programme (Ridolfi et al. Reference Ridolfi2021), and the MeerTime Pulsar Timing Array (MPTA), which studies MSPs with the primary aim of detecting gravitational waves (GWs). Parthasarathy et al. (2021) analysed the pulse-to-pulse variability (‘jitter’) of 29 of these MSPs, placing limits on their timing precision. In this work, we present a census of 189 MSPs visible to MeerKAT at
${\sim} 1400\,\mathrm{MHz}$
frequencies, providing high-time-resolution, polarisation- and flux-calibrated profiles, measured DMs, polarisation fractions, RMs, sub-banded flux densities, and spectral indices, as well as timing potential for the MPTA. The first results of the MPTA will be presented by Miles et al. (in preparation), including a full release of timing residuals and refined ephemerides, and closely followed by an analysis of red noise and GW search (Middleton et al., in preparation).
The 64 13.5-m offset Gregorian MeerKAT dishes have a high aperture efficiency and low system temperature that achieves a system equivalent flux density of just
$\approx 7.0\,\mathrm{Jy}$
at
${\sim} 1400\,\mathrm{MHz}$
frequencies with the full array (Jonas & MeerKAT Team 2016). With an antenna gain roughly 4 times that of Parkes, a lower system temperature (
${\sim} 18\,\mathrm{K}$
), and a larger bandwidth (856 MHz of the MeerKAT L-band receiver compared with the 340 MHz of the Parkes multibeam receiver that was used for much of the last decade for the Parkes Pulsar Timing Array (PPTA; Manchester et al. Reference Manchester2013)), MeerKAT has become the best telescope in the southern hemisphere for a large-scale MSP observing programme and population study (Bailes et al. Reference Bailes2020). Compared to, for example, the Five-hundred-metre Aperture Synthesis Telescope (FAST), which can observe down to
$\mathrm{Dec} >-15\,\mathrm{degrees}$
, MeerKAT has a lower sensitivity but greater sky coverage (
$\mathrm{Dec} <+40\,\mathrm{degrees}$
, which includes the MSP-rich Galactic centre) and significantly higher slew rates (60 and
$120\,\mathrm{deg\,min}^{-1}$
in elevation and azimuth respectively). The 500-m diameter FAST has much superior gain but can only observe about one source every ten minutes due to reconfiguration overheads. The ability to quickly move between sources with minimal overhead is one of the advantages of large-N (number), small-D (diameter) arrays like MeerKAT.
The timing precision and stability of MSPs can additionally be leveraged to search for low-frequency GWs through observations of arrays of MSPs like a galactic-scale interferometer, termed Pulsar Timing Arrays (PTAs; Hellings & Downs Reference Hellings and Downs1983). The current global effort, the International Pulsar Timing Array (IPTA), places stringent constraints on the amplitude of a GW background but no detection has been made (Perera et al. Reference Perera2019), although there are tantalising indications of similar spectral slopes in the red noise of the timing residuals of many of the MSPs with no spatial correlations indicative of a GW background (e.g., Arzoumanian et al. Reference Arzoumanian2020; Chen et al. Reference Chen2021; Goncharov et al. Reference Goncharov2021). While the sensitivity of current PTAs to a GW signal scales favourably with time, it can be greatly accelerated by adding more pulsars to the array and increasing the cadence (Siemens et al. Reference Siemens, Ellis, Jenet and Romano2013). As Parkes is the largest telescope in the southern hemisphere currently contributing to PTA efforts, MeerTime can contribute significantly to the IPTA by (i) observing the current IPTA pulsars with higher precision, (ii) observing additional pulsars not currently included in the IPTA due to low precision, and (iii) helping offset the recent loss of the Arecibo 305-m telescope.
Throughout this paper, we define MSPs as having rotational periods
${<} 50\,\mathrm{ms}$
and period derivatives
${<}2\times10^{-17}\,\mathrm{s\,s}^{-1}$
. In Section 2, we discuss the sources included in this census and the observational parameters. We further discuss the polarisation properties in Section 3, the flux density measurements in Section 4, and the preliminary timing results in Section 5. We conclude with some predictions for the SKA in Section 6. Information on accessing FITS-format files of integrated pulse profiles as well as the full table of results is provided at the end of this manuscript.
Table 1. The 189 pulsars included in the MeerTime census with basic parameters, measured RMs with 1-
$\sigma$
uncertainties, percentages of linear polarisation (
$L/I$
), circular polarisation (
$V/I$
) and absolute circular polarisation (
$|V|/I$
), median uncertainties on the Times of Arrival (ToAs) normalised to 256 s (see Section 5 for details), flux densities at 1 400 MHz, spectral indices from the power law model fit, and references (initial publication). The number of observations included in the analysis for each pulsar is given in the second column. Values less than 1-
$\sigma$
for constrained-positive parameters are given as 2-
$\sigma$
upper limits. The pulsars included in the regular observing programme (88 out of the 89) are indicated with asterisks. RMs measured from summed observations (not the mean of RMs from multiple observations) are indicated with a dagger (
$\dagger$
).
2. Methods
All observations included in this paper were performed with the MeerKAT L-band receiver (856–1 712 MHz) with the Pulsar Timing User Supplied Equipement (PTUSE) back-end that uses coherent dedispersion. A full description of the observing system can be found in Bailes et al. (Reference Bailes2020). Typical observations used 54–61 dishes resulting in a system equivalent flux density of 6.3–7.2 Jy near 1 400 MHz. The system temperature varies as a function of frequency and is slightly worse near the band edges but difficult to measure in the areas of the band permanently affected by radio frequency interference (RFI) (Bailes et al. Reference Bailes2020; Geyer et al. Reference Geyer2021). While the MeerKAT Ultra-High Frequency (UHF) receiver at 544–1 088 MHz is now fully commissioned for pulsar timing, time constraints did not allow for a full MSP census with the UHF receiver. Using the results of this L-band census, a smaller census of low-DM, steep-spectrum sources with the UHF receiver may be feasible, and such sources may be observed with the UHF receiver for the MPTA. The same applies for high-DM, flat-spectrum sources with the MeerKAT S-band receiver in future.
As the original network interface card for the first PTUSE machine was unable to ingest the full bandwidth in ‘1 K mode’ (using 1 024 channels across the 856-MHz band), observations between mid-2019 April and 2020 February were restricted to 928 frequency channels (dropping 48 channels from the top and bottom of the band where the roll-off adversely affects sensitivity in any case), reducing the recorded bandwidth to 775.75 MHz. In order to maintain consistency throughout our analyses, we therefore chose to reduce the observations with 856 MHz of recorded bandwidth down to the same 775.75 MHz. The loss in sensitivity is nearly negligible because of the sharp roll-off at the edges of the receiver band; comparisons of S/N measurements of a sample of 20 pulsars (250 observations) show a median sensitivity loss of only 2.2% (mean of 4.5%).Footnote b Almost all of our pulsars have negative spectral indices (typically between
$-1$
and
$-3$
), which makes the loss of the lower part of the band worse than the top of it. Broader bands also make determination of DMs more accurate, which in turn aids in precision timing. Since late 2020 February, all of our observations have used the entire 856 MHz of bandwidth.
Our source list was derived from the ATNF pulsar catalogue (using v.1.63; Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005), limited to radio-loud MSPS not associated with globular clusters (GCs) and visible to MeerKAT (
$\mathrm{Dec} \leq +30\,\mathrm{degrees}$
to avoid severe time restrictions). We further restricted the list to exclude sources with positional uncertainties greater than 2 arcsec (near the resolution of the tied array beam) or without complete timing solutions (ephemerides) available to us, and we removed 12 Northern sources (
$\mathrm{Dec} >0\,\mathrm{degrees}$
) with known low flux densities (
$S_{1400}<0.1\,\mathrm{mJy}$
), under the assumption that these could be observed with greater efficiency by Northern telescopes and were unlikely to efficiently contribute to the timing array.Footnote c Finally, some sources were removed from our list (after one or more initial observations) due to insufficient precision in ephemeris parameters (leading to significant ‘smearing’ in individual 8-s sub-integrations) or due to low S/N in 1 024-s observations.Footnote d In total, 33 sources were excluded from our original list. To this list, we added 4 unpublished sources (or sources with currently unpublished timing solutions) matching the same sample limits; these MSPs were discovered in the Einstein@Home reprocessing of the Parkes Multibeam Pulsar Survey (Knispel et al. Reference Knispel2013) and the Green Bank North Celestial Cap survey (Stovall et al. Reference Stovall2014). We list our sources with basic parameters, including number of observations, and references in Table 1, where the DMs indicated are fitted from the brightest epoch per source.Footnote e We also plot the sources in a P-
$\dot P$
diagram in Figure 1, where P is the rotation period of the pulsar and the dot denotes its time derivative. We note that, although initial ephemerides from published sources, the ATNF pulsar catalogue, or private communication were used as a starting point, we regularly refined ephemerides to ensure high-quality observations. These updated ephemerides will be presented in future work (Miles et al., in preparation).
Figure 1. A P-
$\dot P$
diagram showing the known MSPs (purple dots) and those included in the MeerTime MSP census project (blue dots). Binary MSPs are outlined with a circle. The data are from the ATNF pulsar catalogue v1.64 (Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005).
Science observations for MeerTime commenced on 2019 February 12, and observations for this census were of a high priority, beginning with the lowest-declination sources that are inaccessible from telescopes in the Northern hemisphere. The main motivation for the census was to quickly establish which pulsars should be included in the PTA programme. For each source, we planned a minimum of 6 observations in order to avoid random scintillation extrema biasing our results when deriving their timing potential and flux densities; due to delays and data quality issues, 4 sources have only 5 observations, and 1 was observed only 4 times. Sources that were found to have good timing precision (
${<}1\,\unicode{x03BC}\mathrm{s}$
uncertainty in
${<}2000\,\mathrm{s}$
)Footnote f were added to a list to be observed with a
${\sim} 2\,\mathrm{week}$
cadence for the MPTA, with source observing times set to achieve sub-
$\unicode{x03BC}\mathrm{s}$
timing precision on average (with a minimum observing time of 256 s to ensure a large fraction of telescope time is spent on-source). This list is updated regularly, to add new pulsars found to have high timing precision and to remove those found not to contribute significantly to the PTA. There are currently 89 that are in the MPTA, and these, excluding one which was included in this analysis due to issues with the ephemeris, are denoted by an asterisk in Table 1 below. In total, we analysed 3 966 observationsFootnote g of 189 MeerTime MSPs from 2019 February to 2021 February. This number includes observations performed for the MeerTime Relativistic Binaries sub-project (Kramer et al. Reference Kramer2021), with which there is considerable overlap of sources; data are shared between MeerTime sub-projects to maximise the science output of the entire Large Survey Project.
The processing of all observations for this project used psrchive (Hotan, van Straten, & Manchester Reference Hotan, van Straten and Manchester2004; van Straten, Demorest, & Oslowski Reference van Straten, Demorest and Oslowski2012), in a pipeline developed by Parthasarathy et al. (2021) which includes RFI excision with a modified version of the CoastGuard software (Lazarus et al. Reference Lazarus, Karuppusamy, Graikou, Caballero, Champion, Lee, Verbiest and Kramer2020) that is optimised for the RFI present at MeerKAT (see, e.g., Bailes et al. Reference Bailes2020). Observations taken prior to mid-April 2020 were polarisation-calibrated with the psrchive tool pac using post-facto derived calibration solutions provided by the South African Radio Astronomy Observatory (SARAO), whereas later observations are polarisation-calibrated at the telescope prior to the data being received by the PTUSE computers (see Serylak et al. Reference Serylak2021, for a full description of both calibration methods). All polarisation values and derivatives follow standard pulsar conventionsFootnote h as described in van Straten et al. (Reference van Straten, Manchester, Johnston and Reynolds2010).
3. Polarisation
For each pulsar, we produce a high S/N profile by summing the brightest individual observationsFootnote i partially averaged in frequency to 232 channels (
$\approx$
3.34 MHz channel widths), and full time integration after summing. We show the polarisation profiles in Figures A.1–A.21, integrated to the centre frequency (after correcting for Faraday rotation as described below). All calculations of linear polarisation, L, have been de-biased with a procedure modified from Everett & Weisberg (Reference Everett and Weisberg2001), where, for every bin i across the profile,
\begin{equation} L_{\textrm{true},i} = \begin{cases} \sqrt{L_{\textrm{meas},i}^2 - \sigma_I^2} & \quad \textrm{if}\ |L_{\textrm{meas},i}| \geq |\sigma_{I}| \\[5pt] -\sqrt{|L_{\textrm{meas},i}^2 - \sigma_I^2|} & \quad \textrm{otherwise}, \end{cases}\end{equation}
where
$L_\textrm{meas}$
is the measured linear polarisation (
$L^2 = Q^2 + U^2$
) and
$\sigma_I$
is the root-mean-square of the total intensity profile in the off-pulse region.Footnote j We determine the uncertainties on the polarisation position angle (PA,
$\psi$
) following Everett & Weisberg (Reference Everett and Weisberg2001): for each bin i across the profile, if
$P_0=L_{\textrm{true},i}/\sigma_{I} > 10$
, the uncertainty is
$\sigma_{\psi,i} = \sigma_I/2L_i$
; otherwise, we determine the uncertainty numerically from the probability distribution (Naghizadeh-Khouei & Clarke Reference Naghizadeh-Khouei and Clarke1993)
\begin{equation} G(\psi, P_0) = \frac{1}{\sqrt{\pi}}\left(\frac{1}{\sqrt{\pi}}+\eta \,e^{\eta^2}[1+\textrm{erf}(\eta)]\right)\,e^{-P_0^2/2},\end{equation}
where
$\eta=\frac{P_0}{\sqrt{2}}\cos2(\psi-\psi_\textrm{true})$
and
${\rm erf(\eta)}$
is the Gaussian error function. The uncertainty,
$\sigma_\psi$
, can therefore be determined by setting
$\psi_\textrm{true}=0$
and adjusting the bounds of integration of the probability distribution to satisfy
\begin{equation} \int_{-1\sigma_\psi}^{1\sigma_\psi} G(\psi,P_0)\,d\psi=68.26\%.\end{equation}
When analysing our pulse profiles with psrchive, it is necessary to consider the noise baseline in each polarisation channel, especially with complicated profiles with emission across the entire phase range. Accurate calibration will set the noise values appropriately, but, when calculating
$S/N$
or polarisation fractions, psrchive will ‘subtract the baseline’ by default. For all but one pulsar in our sample, we use the ‘minimum’ baseline estimator,Footnote k which finds a continuous region with the minimum mean by smoothing the profile with a boxcar with custom widths varying from 1% to 90% (where the region width was determined manually for each pulsar). One pulsar for which the ‘minimum’ baseline estimator was not optimal is PSR
$\mathrm{J}1421-4409$
(Spiewak et al. Reference Spiewak2020), which instead used the ‘normal’ estimator.Footnote l Note that this pulsar still shows apparent over-polarisation at pulse phases
${\sim}$
0.6–1.0 (shown in the central panels of Figure A.7), as there is significant emission in both Q and U throughout that range. This pulsar may be similar to PSR J0218+4232 with underlying unpulsed emission (Navarro et al. Reference Navarro, de Bruyn, Frail, Kulkarni and Lyne1995), which would contradict the general assumption that all polarisation channels are consistent with noise over some phase range (the off-pulse baseline). Further study of this pulsar with MeerKAT could reveal the nature of this emission.
We measure significant fractional linear polarisation (
$L/I$
; from fully time- and frequency-integrated profiles centred at 1 284 MHz, as shown in Figures A.1–A.21) for 180 pulsars in our sample (
${>}$
1-
$\sigma$
significance), and significant absolute fractional circular polarisation (
$|V|/I$
) for 119. Our full results are listed in Table 1.
We calculate the RM for each pulsar from the individual observations (fully integrated in time, with 29 frequency channels across the 775.75 MHz band) or, for faint pulsars, from the summed observations (also fully time-integrated, with 29 frequency channels) and list all in Table 1. We use rmfit to determine RMs using a brute force linear polarisation maximisation which is then refined using an iterative fit to the measured PA as a function of frequency. After calculating RM from the individual observations, we then correct for the contributions of the ionosphere using the ionFR software (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013) with IGSG maps.Footnote m For each pulsar with
${\geq} 10$
corrected RMs, we remove outliers using a basic drop-out algorithm comparing the standard deviation and median-absolute-deviation from the median. Outliers are removed manually for pulsars with fewer observations. We then report the mean of the corrected RM values with the standard deviation as the 1-
$\sigma$
uncertainty. For faint pulsars, because we measure the RM from a summed profile, we report the RMs and uncertainties as given by rmfit after correcting by the mean of the ionospheric contributions per pulsar (the uncertainties on the ionospheric corrections are summed in quadrature with the uncertainties given by rmfit). No RMs are given for pulsars with linear polarisation fractions less than
$\approx0.05$
(
${\sim}$
1.5-
$\sigma$
).
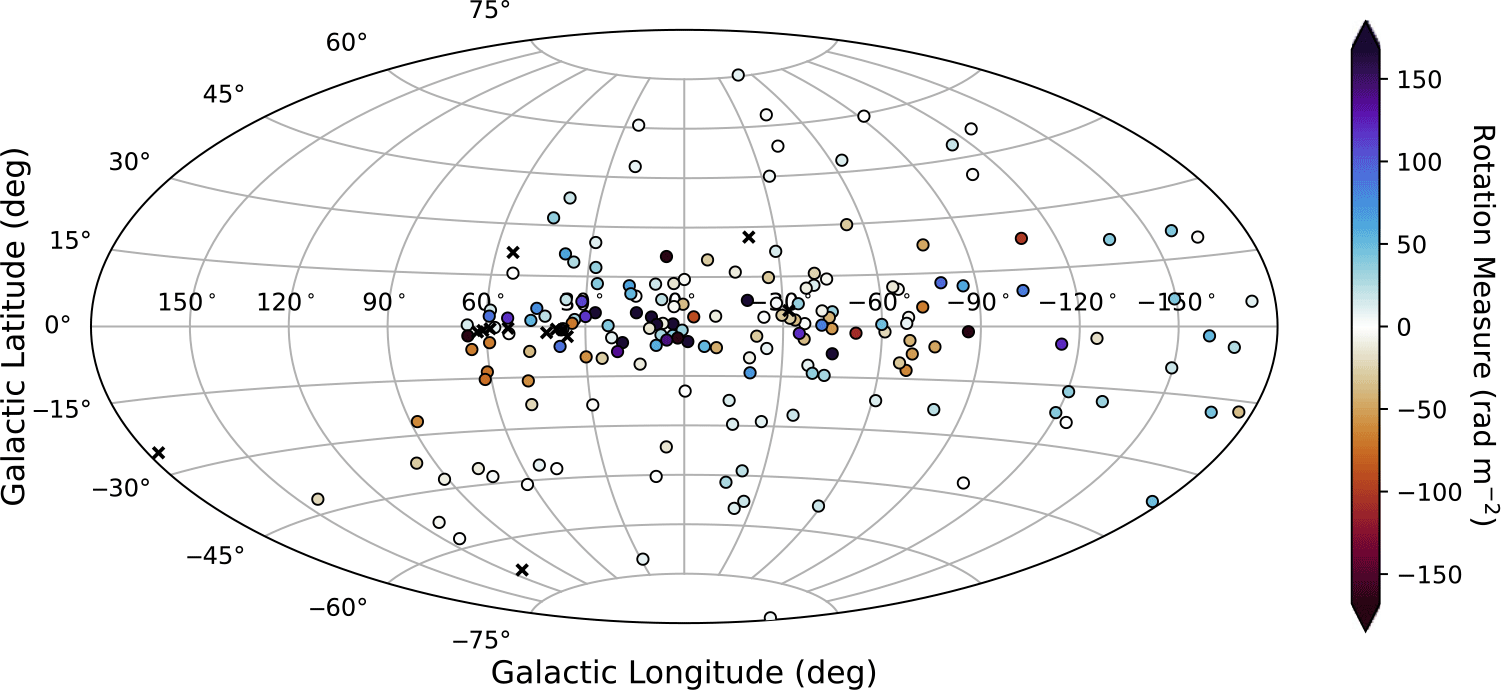
Figure 2. The positions of the MSPs in this sample on an Aitoff projection, with coloured circles indicating sources with measured RMs (including those formally consistent with zero) and black ‘x’ markers indicating sources without measured RMs, as described in the text.
In total, we measure 171 non-zero RMs (at the 1-
$\sigma$
level; 163 with 3-
$\sigma$
measurements), increasing the number of MSPs with known RMs by 88. To verify the reliability of our measurements, we compare the RMs in the ATNF pulsar catalogue (v1.64) for the 83 MSPs with previously published values and calculate the significance of the difference of the values:
$d = \left(\textrm{RM}_\textrm{psrcat} - \textrm{RM}_\textrm{census}\right)/\sqrt{\sigma_\textrm{psrcat}^2 + \sigma_\textrm{census}^2}$
. Nearly 50% of the pulsars have RMs that are 1-
$\sigma$
consistent with the previously published values, and 85% of the pairs are consistent to 2.6-
$\sigma$
. Given that pulsar RMs are known to vary with time due to inaccurate models of the ionospheric Faraday rotation (e.g., Yan et al. Reference Yan2011), that not all values reported in the ATNF pulsar catalogue are corrected for the ionosphere, and that measurements at different frequencies can result in statistically inconsistent RMs (see, e.g., the position angle fits in Dai et al. Reference Dai2015), differences between our RMs and published values at this level are not unexpected. However, two pulsars have significantly different values in our census and the literature: PSR
$\mathrm{J}1502-6752$
has a published value of
$-225(2)\,\mathrm{rad\,m}^{-2}$
from Keith et al. (Reference Keith2012), while our measurement is
$232.8(2)\,\mathrm{rad\,m}^{-2}$
; and PSR J0154+1833 has a published value of
$21.6(1)\,\mathrm{rad\,m}^{-2}$
(Martinez et al. Reference Martinez2019), while our measurement is
$-21.9(6)\,\mathrm{rad\,m}^{-2}$
. Given the consistency of our other RM measurements, we are inclined to believe the Keith et al. (Reference Keith2012) and Martinez et al. (Reference Martinez2019) values suffer from a sign convention error.
We show in Figure 2 the positions of the MSPs in our sample, coloured by their measured RM (black marks indicate the positions of pulsars without measured RMs). Overall, the RMs for our sample do not indicate strong (average) magnetic fields along the lines of sight, with 90% of values in the range
$-2.8$
–
$2.3\,\unicode{x03BC}\mathrm{G}$
(full range
$-6.7$
–
$5.0\,\unicode{x03BC}\mathrm{G}$
).
4. Flux densities and spectral indices
Ideally, pulsar flux densities are obtained using an injected and pulsed broadband calibration signal that can be measured against a source of known flux density to derive a flux scale. While attempting to derive a polarisation calibration solution using the MeerKAT L-Band receiver pulsed cal, we found that the degree of polarisation of the cal often exceeds 105%. This is probably due to the strength of the cal being comparable to the system equivalent flux density and driving the system into a non-linear regime. This made this conventional method unsuitable for absolute flux calibration.
An alternative calibration method involves using the radiometer equation and assuming that the rms of the pulsar baseline region is well-defined by the system equivalent flux density plus the galactic sky temperature divided by the antenna gain. In the presence of unrecognised sources of noise due to RFI, this method can underestimate radio fluxes and must be approached with caution. Nevertheless, as shown in Bailes et al. (Reference Bailes2020), there are many parts of the MeerKAT L-band (856–1 712 MHz) that are almost always devoid of interference, and we found that many of our high DM (
$\mathrm{DM}\,\gtrsim100\,\mathrm{pc\,cm}^{-3}$
) sources gave very reliable S/N and hence flux values from epoch to epoch across much of the band. To assess the reliability of this method, we computed the modulation indices of the derived flux densities for the five pulsars with the largest DMs in our sample and found them to be between 7–15%, which means that the reliability of the flux densities from epoch to epoch is probably no worse than this figure.
Absolute flux densities for each observation were thus calculated using the radiometer equation and assuming the Haslam et al. (Reference Haslam, Klein, Salter, Stoffel, Wilson, Cleary, Cooke and Thomasson1981) sky temperatures scale as the observing frequency to the power
$-2.55$
(Lawson et al. Reference Lawson, Mayer, Osborne and Parkinson1987). To determine mean pulsar flux densities the integrated flux above a baseline is often computed by firstly converting the counts to Jy in a calibration procedure. The mean pulsed flux is then just the integral of the flux above a defined baseline divided by the number of bins. Millisecond pulsars can have profiles that are very complex and this makes baseline estimation difficult if using a simple boxcar, especially if it extends into the wings of the pulse profile. For every MSP, the ideal boxcar width will differ, or even require multiple disjoint sections, so we used an interactive tool to define the baseline through visual inspection for each pulsar from high S/N observations to help determine the rms of the noise in the baseline. Software was written to cross-correlate the template with each profile, and the rms residual of the phase-aligned profiles in the baseline region was evaluated.
There are sections of the MeerKAT band that are rarely affected by RFI (see Bailes et al. Reference Bailes2020), and these were used to determine the flux density in those bands. We found that many of the high-DM MSPs that would be expected to have consistent epoch to epoch flux densities often exhibited dips in their mean spectra where RFI is regularly present in the fourth of the 8 sub-bands. As an example, for PSR
$\mathrm{J}1017-7156$
, the off-pulse rms was roughly 5–21% higher in this band with a mean 10% higher after our attempts at RFI removal with CoastGuard. Scaling the flux densities of all channels by the ratio of their off-pulse rms counts to that of the median off-pulse rms counts led to mean spectra largely free of this dip in channel 4 and was performed on all the data.
After integrating all of the observations for each pulsar, the vast majority of our pulsars were shown to have a smooth power law variation of mean flux density with frequency as is often seen in the population between 1–1.7 GHz, especially those at high dispersion (
${\gtrsim} 100\,\mathrm{pc\,cm}^{-3}$
) where strong scintillation events across
${\sim}$
100-MHz bands are not seen (Dai et al. Reference Dai2015; see also Figure 3, showing PSRs
$\mathrm{J}1017-7156$
,
$\mathrm{J}1600-3053$
, and
$\mathrm{J}2241-5236$
, with DMs of 94.2, 52.3, and
$11.4\,\mathrm{pc\,cm}^{-3}$
, respectively). To derive spectral indices and normalise our flux density measurements to a standard frequency (1 400 MHz), we fitted a power law model,
$S = S_{1400}\,(\nu/1400\,\textrm{MHz})^\alpha$
, to the mean flux density in each of 8 sub-bands across the 775.75 MHz band,Footnote n and our results are listed in Table 1. In Figure 3, we show an example of the flux density measurements and best-fitting models for 3 pulsars with varying DM values, selected for comparison with the study by Dai et al. (Reference Dai2015) on pulsars in the PPTA (Kerr et al. Reference Kerr2020).
Figure 3. Mean flux density measurements for 3 pulsars, PSRs
$\mathrm{J}1017-7156$
(blue squares;
$N_{\rm obs}=51$
),
$\mathrm{J}1600-3053$
(green stars;
$N_{\rm obs}=33$
), and
$\mathrm{J}2241-5236$
(pink circles;
$N_{\rm obs}=42$
), fit with power law models (blue dashed, green dotted, and pink dash-dotted lines, respectively) to determine
$S_{1400}$
and the spectral index,
$\alpha$
. The power law models for these pulsars are:
$S_{1017} = 1.09\,{\rm mJy} \times(\nu/1400\,{\rm MHz})^{-2.01}$
,
$S_{1\,600} = 2.22\,{\rm mJy} \times(\nu/1400\,{\rm MHz})^{-0.99}$
, and
$S_{2\,241} = 1.83\,{\rm mJy} \times(\nu/1400\,{\rm MHz})^{-3.20}$
. The error bars indicate the formal error on the means.
We refer the reader to Gitika et al. (in preparation) for a thorough analysis of the flux density measurements from these and more recent MeerTime MSP observations, and here we provide a simple comparison of our results with overlapping samples from Dai et al. (Reference Dai2015) and Alam et al. (Reference Alam2021a) to verify the accuracy of our method. Note that the Dai et al. (Reference Dai2015) spectral indices were derived from flux density measurements in 3 bands centred at 732, 1 369, and 3 100 MHz, and therefore they may be sensitive to, e.g., spectral turn-over, which is possibly seen in their analysis of PSR
$\mathrm{J}1600-3053$
. With this caveat, we find good agreement between our
$S_{1400}$
values and spectral indices and those of Dai et al. (Reference Dai2015), with PSR
$\mathrm{J}1744-1134$
showing the greatest disparities in both
$S_{1400}$
and spectral index (although the values are consistent at the 2-
$\sigma$
level and this pulsar has a very small DM which makes it prone to large flux density variations). The flux density of this pulsar in the 97-Mhz sub-band centred at 1 429 MHz varied from 0.14 to 14 mJy with a mean of 3.7 mJy and a standard deviation of 4.0 mJy. Thus its difference in mean flux density is not that worrying.
Recently, the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) collaboration presented a comprehensive study of flux densities for its sample with which we have significant overlap (Alam et al. Reference Alam2021a). Of the 15 non-PPTA pulsars for which we have common data, 12 had flux densities within
${\sim}$
30% of our values and those with the largest deviations (differing by roughly a factor of 2 from our values) have low DMs. Alam et al. (Reference Alam2021a) pointed out that the median flux they obtained for PSR J2317+1439 (
$0.45^{+0.35}_{-0.19}\,\mathrm{mJy}$
) differed from the catalogue flux density of 4(1) mJy significantly.Footnote o Our mean value 0.60(6) mJy (median of 0.37 mJy) is much closer to the Alam et al. (Reference Alam2021a) result, and we note that this pulsar scintillates strongly. The pulsar with the most observations (134 with reliable fluxes) was PSR
$\mathrm{J}1909-3744$
. Alam et al. (Reference Alam2021a) measured a median flux density at 1 400 MHz of 1.03 mJy, matching our median value precisely, which gives us great confidence in our relative flux density scales. This pulsar experiences extreme scintillation events, and our measured mean flux density was 1.80(9) mJy. Dai et al. (Reference Dai2015) recorded a mean flux density for PSR
$\mathrm{J}1909-3744$
of 2.5(2) mJy at 1 400 MHz. Note also that different observing strategies can lead to biases in observed flux density distributions. MeerKAT observations use a queue system with minimal intervention (and NANOGrav observations are run with minimal intervention), while observations for the PPTA are done manually, and observers are encouraged to switch sources when the source
$S/N$
is low and to repeat observations when the
$S/N$
is high. This leads to better uncertainties on the ToAs but biases the flux density distributions to higher values, which is consistent with our results.
Overall, we find a mean spectral index of
$-1.92(6)$
, with a standard deviation of 0.6, for our sample of 189 pulsars, and we show the full distribution of spectral indices in Figure 4. This mean is consistent at the 2-
$\sigma$
level with that found by Dai et al. (Reference Dai2015), who found a value of
$-1.81(1)$
, as well as previous results for MSP studies (Toscano et al. Reference Toscano, Bailes and Manchester1998; Kramer et al. Reference Kramer, Lange, Lorimer, Backer, Xilouris, Jessner and Wielebinski1999) and studies of normal pulsars (Jankowski et al. Reference Jankowski, van Straten, Keane, Bailes, Barr, Johnston and Kerr2018). The typical uncertainties on the spectral indices for pulsars with
${>} 10$
observations are
${\sim}0.1$
, with 95% of the uncertainties
${<} 0.4$
. These results could be improved in future using the MeerKAT UHF and S-band receivers to increase the frequency coverage.
Figure 4. Histogram of spectral indices. In green, we show the spectral indices for pulsars with
$\mathrm{DM} > 100\,\mathrm{pc\,cm}^{-3}$
(and therefore low scintillation) and those with
${>} 10$
observations to reduce the impact of scintillation on the measurements. We show the remaining spectral indices in our sample in the blue histogram.
5. Timing results
For all pulsars in this study, we list basic parameters in Table 1, and provide our measured median ToA uncertainties. The templates used for our standard timing procedure are produced from summed, temporally-integrated observations with 232 frequency channels across the 775.75-MHz band. From these high-S/N observations, we then derive pulse ‘portraits’ using the PulsePortraiture software (Pennucci Reference Pennucci2019) and produce noise-free templates with 8 sub-bands for timing.Footnote
p
We use the ‘Fourier Domain with Markov chain Monte Carlo’ (FDM) fitting algorithm from pat in psrchive to produce ToAs from archives partially-integrated to 256-s sub-integrations and 8 sub-bands across the 775.75-MHz band (
${\sim} 97$
-MHz sub-bands). We compute ‘typical’ ToA uncertainties per pulsar by first normalising the measured uncertainties to the nominal minimum observing time, 256 s, then calculating the error on the weighted mean ToA for each sub-integration as
\begin{equation} \frac{1}{\sigma_\textrm{sub}^2} = \sum_i \frac{1}{\sigma_{\textrm{sub,}i}^2} ,\end{equation}
where i represents the frequency channels, and finally returning the median of the resulting
$\sigma_\textrm{sub}$
values as the typical ToA uncertainty. We note that this method approximates the ToA uncertainty achievable by proper wideband timing using a 2-dimensional template (i.e., returning a single ToA per sub-integration). We summarise the resulting median ToA uncertainties in Figure 5, showing the cumulative histogram of the median uncertainties. Note that the median ToA uncertainties should not be confused with the ultimate fitted rms residuals, as they do not factor in pulse jitter nor the deleterious effects of red noise.
Figure 5. Cumulative histogram of median ToA uncertainties from 97-MHz, 256-s sub-integrations, scaled to the full 775.75 MHz, on a logarithmic scale. From these data, 77 pulsars have sub-microsecond (median) timing precision in less than 256 s.
5.1. Timing forecast
In assembling a large dataset of MSP data across a minimum timespan of six months, we are able to determine the timing potential for each source and inform future studies. The potential for MeerTime to contribute to global efforts to detect GWs with the IPTA can be estimated from these data. As mentioned in Section 2, we continue to regularly observe pulsars that have low ToA uncertainties,
$\sigma_\tau<1\,\unicode{x03BC}\mathrm{s}$
, calculated using frequency-scrunched templatesFootnote q and observations with integration times,
${256} < T_\textrm{obs}<2000\,\mathrm{s}$
.
To compare the sensitivity of PTA observations with MeerKAT to other current programmes, and its potential impact on global efforts, we consider the detection of a GW background (assuming a strain spectrum of
$h_c(f) = 1.9\times 10^{-15} (f/1\,{\rm yr})^{-2/3}$
; e.g., Siemens et al. Reference Siemens, Ellis, Jenet and Romano2013) through correlations between pulsars in the array (Hellings & Downs Reference Hellings and Downs1983). The background is chosen to be the amplitude of the apparent common red noise found in analysis of the NANOGrav 12.5-yr data release (Alam et al. Reference Alam2021b). We can approximate the sensitivity of a given PTA to both the autocorrelated signal (the ‘pulsar term’) and the cross-correlated signal (the ‘Earth term’), following Siemens et al. (Reference Siemens, Ellis, Jenet and Romano2013).Footnote r They construct matched detection statistics in the Fourier domain (see their Equation (17)) and calculate how the
$S/N$
of the detection statistic depends on the noise properties of the array.
The expected
$S/N$
in the autocorrelations is
\begin{align} \rho_{ACF}^2 = \sum_{p=1}^{N_p} \sum_{k=1}^{N_f} \frac{P_g^2(f_k)}{P_{p}^2(f_k)},\end{align}
where
$P_g(f_k)$
is the power spectral density of the GWB in frequency channel
$f_k$
, where
$k=1,N_f$
is a Fourier series starting
$1/T_{eff}$
at the reciprocal of the common effective observing
$T_{\rm eff}$
.
$P_{p}(f_k)=P_g(f_k) + P_{p,r}(f_k) + P_{p,w}$
is the total power (the sum of the GWB and the red noise (
$P_{p,r}$
) and the white noise (
$P_{w,r}$
) in the same channel for pulsar p.
The expected
$S/N$
in the cross-correlations is found as the
$S/N$
of a matched filter with the Hellings-Downs correlation function
\begin{align} \rho^2 = \sum_{i=1}^{N_p-1} \sum_{j=i+1}^{N_p} \chi^2_{ij} \sum_{k=1}^{N_f} \frac{P^2_g(f_k)}{P_{p_i}(f_k) P_{p_j}(f_k)},\end{align}
where
$\chi_{ij}$
are the angular correlation coefficients (Hellings & Downs Reference Hellings and Downs1983)
\begin{align}\chi_{ij} = \frac{3}{4} \left(1 - \cos(\theta_{ij})\right) \log \left(1 - \cos(\theta_{ij})\right) -\frac{1}{8} \left( 1 - \cos(\theta_{ij}) \right) + \frac{1}{2}\nonumber\\[5pt]\end{align}
We use the published source lists, median pulsar timing precisions, timespans, cadences, and observational parameters from the European Pulsar Timing Array (EPTA; Desvignes et al. Reference Desvignes2016), NANOGrav (Alam et al. Reference Alam2021b), and the PPTA (Kerr et al. Reference Kerr2020) to form a representative sample of the IPTA. For sources in multiple PTAs, the data set with the longest time span is used. We show how the S/N for this background increases with time in Figure 6.
Figure 6. Comparison of PTA sensitivity to the cross-correlated component of the GW background (solid lines) and the uncorrelated signal (dashed lines), using the current MeerTime timing programme with 89 pulsars (blue lines), the EPTA programme with 42 pulsars (orange lines), the NANOGrav programme with 47 sources (red lines), the PPTA with 26 (brown lines), or the IPTA as the union of the four (black lines).
For the NANOGrav sensitivity curves, we have assumed that the Arecibo timing programme ceased in 2020 August and that the pulsars are not observed elsewhere, which demonstrates the importance of Arecibo to international pulsar timing efforts. The modelling includes red noise in the sensitivity estimates, for pulsars where red noise has previously been detected (Arzoumanian et al. Reference Arzoumanian2020; Goncharov et al. Reference Goncharov2021). Undetected red noise is likely to be present in some of the pulsars timed by MeerKAT, which will affect our sensitivity estimates.
These calculations imply that the MPTA will be comparable in sensitivity to the PPTA by 2023, NANOGrav by 2024, and the EPTA by
$\approx 2025$
. In less than four years, the MPTA will be contributing to the IPTA effort. As the MeerKAT timing array programme has observed a large number of pulsars from its start, the sensitivity to the cross-correlated signal (dashed lines) is always comparable to the auto-correlated signal, similar to the EPTA with its 42 pulsars. In contrast, the PPTA project includes only 26 pulsars, and NANOGrav started out with a smaller number of pulsars before gradually increasing in size starting in 2009, and, in the most recent data release (12.5-yr), they listed 47 pulsars (Alam et al. Reference Alam2021b). The MPTA could be expanded in the future with timing of additional pulsars in other bands or timing of MSPs discovered by MeerKAT and other facilities. Future work by Middleton et al. (in preparation) will examine the sensitivity of the MPTA and potential improvements.
6. Summary
In this work, we demonstrated the outstanding potential of MeerKAT for precision pulsar timing of MSPs with this initial census, analysing polarisation properties, flux densities and spectral indices, and timing precision. We presented a dataset of nearly 4 000 observations of 189 pulsars, spanning 24 months, including polarisation-calibrated profiles and high-precision ToAs. Our timing simulations offer simple predictions of future results, and we predict that the MPTA will be a major contributor to global PTA efforts within the next 5 yr. More work is forthcoming, including the first MPTA data release with full timing and noise analyses (Miles et al., in preparation), an analysis of flux density measurements for MeerTime MSPs (Gitika et al., in preparation), and a study of the sensitivity of the MPTA and potential for improvements (Middleton et al., in preparation).
Acknowledgements
The authors thank the expert reviewers for providing thorough and thoughtful comments on this manuscript. The authors additionally thank R. Eatough, D. Lorimer, and J. Swiggum for providing phase-connected pulsar ephemerides for unpublished pulsars. The MeerKAT telescope is operated by SARAO, which is a facility of the National Research Foundation, an agency of the Department of Science and Innovation. PTUSE was developed with support from the Australian SKA Office and Swinburne University of Technology, with financial contributions from the MeerTime collaboration members. This research was funded partially by the Australian Government through the Australian Research Council (ARC), grants CE170100004 (OzGrav) and FL150100148. RMS acknowledges support through ARC Future Fellowship FT190100155. This work used the OzSTAR national facility at Swinburne University of Technology. OzSTAR is funded by Swinburne University of Technology and the National Collaborative Research Infrastructure Strategy (NCRIS). This research made use of astropy, a community-developed core Python package for Astronomy (Price-Whelan et al. Reference Price-Whelan2018), the matplotlib package (v1.5.1; Hunter Reference Hunter2007), and psrqpy, a Python package for searching the ATNF Pulsar Catalogue (Pitkin Reference Pitkin2018).
Data Availability
We have made available all 189 polarisation profiles, as shown in Figures A.1–A.21, in PSRFITS format with full phase resolution (1 024 bins), 4 polarisation channels, and 8 frequency channels across the 775.75-MHz band, as well as the table containing the analysis results. The table, in csv format with 189 rows, contains mean flux densities (and standard deviations) in 8 frequency bands per pulsar, spectral indices and fit
$S_{1400}$
values with uncertainties, median timing uncertainties as described in Section 5, polarisation fractions and rotation measures, dispersion measures and reference epochs, and basic pulsar properties (rotation properties and positions) for easy reference. The dataset will be made available prior to publication of this manuscript, under the DOI 10.5281/zenodo.5347875.
A. Polarisation Profiles
Figure A.1. Polarisation profiles for MSPs from the MeerTime Census project, fully integrated from the 775.75-MHz band centred at 1 284 MHz, with polarisation position angles in the upper panels (not corrected to infinite frequency). The black solid line indicates the total intensity, the red dashed line shows the linearly polarised emission, and the blue dotted line shows the circularly polarised emission. All profiles show the phase range (
$-$
0.05, 1.05), and P.A.s are plotted over the range (
$-$
135, 135) degrees. The period and DM of each source is listed in the upper left corner, in units of ms and
$\mathrm{pc\,cm}^{-3}$
, respectively. In the upper right corner, we indicate the number of phase bins used (256 for
$P<15\,\mathrm{ms}$
and low
$S/N$
) and the normalisation factor (peak flux density at 1 284 MHz in mJy).
Figure A.2. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.3. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.4. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.5. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.6. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.7. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.8. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.9. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.10. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.11. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.12. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.13. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.14. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.15. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.16. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.17. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.18. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.19. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.20. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Figure A.21. Polarisation profiles for MSPs from the MeerTime Census project, as Figure A.1.
Open access
