1. Introduction
Astrophysical sources of microwave radiation with extremely high spectral brightness/temperature (compact structures in certain star-formation regions, compact structures in spreading cold stellar mantles, structures in the atmospheres of Mars and Venus radiating at vibration transitions of CO2 molecules, etc.) are interpreted as astrophysical masers. The attribution of these astrophysical sources as masers is mainly based on their high brightness. However, despite certain successes, the maser model of these sources has unresolved difficulties. In particular, pumping mechanisms that ensure that the lasing threshold is exceeded are still being discussed; there is no good explanation for the periodicity of radiation, which ranges from minutes to tens of years. The most difficult thing to explain is that the correlation between brightness and linewidth is observed quite rarely. This correlation is an important characteristic of all lasers, but mostly not observed (Desmurs et al. Reference Desmurs, Baudry, Wilson, Cohen and Tofani1998; Lekht 1999; Etoka et al. Reference Etoka, Blaszkiewicz, Szymczak and Le Squeren2001; Fish, Brisken, & Sjouwerman. Reference Fish, Brisken and Sjouwerman2006; Moscadelli et al. Reference Moscadelli, Menten, Walmsley and Raid2003). In addition, the huge number of maser sources in space is amazing, while obtaining it in the laboratory requires significant efforts.
In addition to maser sources, there is a number of other astrophysical sources of intense radiation. These are, for example, synchrotron radiation, radiation of quasars, radiation as a result of Compton back-scattering, etc.; their temperatures can be very high. And a question appears: is the mechanism of the stimulated emission of radiation unique for providing the extremely high brightness of radiation? In particular, radiation in the radiofrequency range resulting from luminescence can cause a high, up to 1011–1012 K, radiation temperature of objects traditionally considered as astrophysical masers (Shepelev Reference Shepelev2007).
By itself, the high temperature/brightness of the radiation does not make it possible to establish whether the radiation is thermal or maser; this can be established on the basis of measuring the statistical properties of high-order correlation functions. Quite a number of works are devoted to the problem of research and analysis of high-order correlation functions for radiation from astrophysical objects (see, for example, Foellmi Reference Foellmi2009; Hirata & McQuin Reference Hirata and McQuinn2014). When measuring the statistical characteristics of astrophysical masers, it was found (Evans et al. Reference Evans, Hills, Rydbeck and Kollberg1972) that the statistics is close to that of the Gaussian radiation. However, for sufficiently powerful astrophysical masers, the statistics may differ significantly from the Gaussian one (Dinh-V-Trung 2009). If the saturation level is high, this difference can be described in terms of the changes in the relationships for the radiation phases (Gray & Bewley Reference Gray and Bewley2003).
The methods developed in quantum optics, which are also applicable in the classical case, make it possible to determine the maser or thermal nature of the radiation of astrophysical masers by the value of two parameters: the average intensity and the dispersion of the average intensity. It should be noted that thermal radiation means the radiation from any source with the same statistical characteristics as equilibrium radiation. This interpretation expands the concept of thermal radiation and is applicable in this work.
2. Correlation functions of thermal and maser radiation
The intensity (power density) of the radiation of a stationary process is defined as a first-order correlation function for an electric field taken at a fixed point:
Averaging is carried out over a time
![]() $\tau $
that is much higher than the inverse radiation frequency
$\tau $
that is much higher than the inverse radiation frequency
![]() $ {\nu ^{ - 1}} $
. If, in this case,
$ {\nu ^{ - 1}} $
. If, in this case,
![]() $\tau$
is much less than the reciprocal of the emission bandwidth
$\tau$
is much less than the reciprocal of the emission bandwidth
![]() $\Delta {\nu ^{ - 1}}$
, the intensity fluctuations are recorded accurately. Thus, the condition for
$\Delta {\nu ^{ - 1}}$
, the intensity fluctuations are recorded accurately. Thus, the condition for
![]() $\tau $
must be satisfied
$\tau $
must be satisfied
The spatial coherence function at points 1 and 2 is
Here,
![]() ${E^{\left( + \right)}}$
is an analytical signal (Gabor Reference Gabor1946; Klauder & Sudarshan Reference Klauder and Sudarshan1968),
${E^{\left( + \right)}}$
is an analytical signal (Gabor Reference Gabor1946; Klauder & Sudarshan Reference Klauder and Sudarshan1968),
![]() ${E^{\left( - \right)}} = {E^{\left( + \right)}}^*$
. The mean square of the intensity
${E^{\left( - \right)}} = {E^{\left( + \right)}}^*$
. The mean square of the intensity
![]() $\left\langle {I_{11}^2} \right\rangle $
and its variance
$\left\langle {I_{11}^2} \right\rangle $
and its variance
![]() $\left\langle {\Delta I_{11}^2} \right\rangle $
are determined in a standard way:
$\left\langle {\Delta I_{11}^2} \right\rangle $
are determined in a standard way:
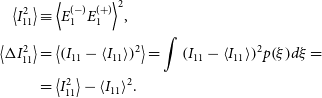 \begin{align}
\left\langle {I_{11}^2} \right\rangle & \equiv {\left\langle {E_1^{( - )}E_1^{( + )}} \right\rangle ^2},\nonumber\\
\left\langle {\Delta I_{11}^2} \right\rangle & = \left\langle {{{\left( {{I_{11}} - \left\langle {{I_{11}}} \right\rangle } \right)}^2}} \right\rangle = \int {{{\left( {{I_{11}} - \left\langle {{I_{11}}} \right\rangle } \right)}^2}} p\!\left( \xi \right)\!d\xi =\\
& = \left\langle {I_{11}^2} \right\rangle - {\left\langle {{I_{11}}} \right\rangle ^2}.\nonumber \end{align}
\begin{align}
\left\langle {I_{11}^2} \right\rangle & \equiv {\left\langle {E_1^{( - )}E_1^{( + )}} \right\rangle ^2},\nonumber\\
\left\langle {\Delta I_{11}^2} \right\rangle & = \left\langle {{{\left( {{I_{11}} - \left\langle {{I_{11}}} \right\rangle } \right)}^2}} \right\rangle = \int {{{\left( {{I_{11}} - \left\langle {{I_{11}}} \right\rangle } \right)}^2}} p\!\left( \xi \right)\!d\xi =\\
& = \left\langle {I_{11}^2} \right\rangle - {\left\langle {{I_{11}}} \right\rangle ^2}.\nonumber \end{align}
Here,
![]() $p\!\left(\xi \right)$
is the distribution function,
$p\!\left(\xi \right)$
is the distribution function,
![]() $\int\!{p\!\left( \xi \right)\!d\xi = } 1$
. The value
$\int\!{p\!\left( \xi \right)\!d\xi = } 1$
. The value
(
![]() ${x_i} = \left\{ {{{\textbf{r}}_i},{t_i}} \right\}$
is the set of space-time variables) is the intensity correlation function, and
${x_i} = \left\{ {{{\textbf{r}}_i},{t_i}} \right\}$
is the set of space-time variables) is the intensity correlation function, and
is the normalised second-order coherence function.
The value of
![]() $g_{12}^{(2)}$
depends on
$g_{12}^{(2)}$
depends on
![]() ${x_1}$
and
${x_1}$
and
![]() ${x_2}$
. Spatial region in the far field, in which the condition
${x_2}$
. Spatial region in the far field, in which the condition
is satisfied, is the volume of coherence (Mandel & Wolf Reference Mandel and Wolf1995). Here,
is the spatial coherence radius,
![]() $\lambda $
is a central radiation wavelength,
$\lambda $
is a central radiation wavelength,
![]() $\Delta \theta $
is an angle at which the source is observed;
$\Delta \theta $
is an angle at which the source is observed;
is a longitudinal coherence length,
![]() $\Delta \lambda $
is a half-width of the emission line. The coherence time
$\Delta \lambda $
is a half-width of the emission line. The coherence time
![]() ${t_{coh}}$
is inversely proportional to the frequency half-width of the line:
${t_{coh}}$
is inversely proportional to the frequency half-width of the line:
Radiation within the coherence volume can be considered as a single-mode one (Klyshko Reference Klyshko2011; Scully & Zubairy Reference Scully and Zubairy1997).
If the condition
is met, then the ratio
is true with high precision. A value of the degenerate normalised second-order autocorrelation function
![]() $g_{11}^{(2)}$
(named as ‘the bunching parameter’ in quantum optics) is determined according to Equations (4) and (5).
$g_{11}^{(2)}$
(named as ‘the bunching parameter’ in quantum optics) is determined according to Equations (4) and (5).
Statistical parameters of radiation depend on both classical and quantum fluctuations, which has been shown first by Albert Einstein (Einstein Reference Einstein1909). The quantum fluctuations are rather small and may not be taken into account in comparison with classical fluctuations in the case when the degeneracy factor
![]() $\left\langle N \right\rangle $
(the ratio between the radiation energy in the coherence volume and the photon energy) significantly exceeds unity (Klyshko Reference Klyshko2011; Scully & Zubairy Reference Scully and Zubairy1997). The degeneracy factor is equal to
$\left\langle N \right\rangle $
(the ratio between the radiation energy in the coherence volume and the photon energy) significantly exceeds unity (Klyshko Reference Klyshko2011; Scully & Zubairy Reference Scully and Zubairy1997). The degeneracy factor is equal to
Consequently, in the Rayleigh-Jeans limit, the quantum intensity fluctuations are insignificant in comparison with the classical ones.
In the Rayleigh-Jeans limit, in the volume of coherence, that is for one mode, the intensity distribution functions have the forms (Klyshko Reference Klyshko2011)
for the thermal radiation, and
for the maser emission. Thus, in accordance to Equation (3), the intensity dispersion for thermal radiation is calculated as
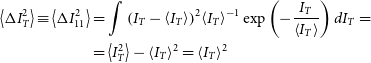 \begin{align}
\left\langle {\Delta I_T^2} \right\rangle \equiv \left\langle {\Delta I_{11}^2} \right\rangle & = {\int {\left( {{I_T} - \left\langle {{I_T}} \right\rangle } \right)} ^2}{\left\langle {{I_T}} \right\rangle ^{ - 1}}\exp \left( { - \frac{{{I_T}}}{{\left\langle {{I_T}} \right\rangle }}} \right)d{I_T} = \nonumber\\
& = \left\langle {I_T^2} \right\rangle - {\left\langle {{I_T}} \right\rangle ^2} = {\left\langle {{I_T}} \right\rangle ^2}\end{align}
\begin{align}
\left\langle {\Delta I_T^2} \right\rangle \equiv \left\langle {\Delta I_{11}^2} \right\rangle & = {\int {\left( {{I_T} - \left\langle {{I_T}} \right\rangle } \right)} ^2}{\left\langle {{I_T}} \right\rangle ^{ - 1}}\exp \left( { - \frac{{{I_T}}}{{\left\langle {{I_T}} \right\rangle }}} \right)d{I_T} = \nonumber\\
& = \left\langle {I_T^2} \right\rangle - {\left\langle {{I_T}} \right\rangle ^2} = {\left\langle {{I_T}} \right\rangle ^2}\end{align}
and, for the maser emission, as
Here, intensities of thermal and maser radiation, determined according to general Equation (1), are denoted as
![]() ${I_T}$
and
${I_T}$
and
![]() ${I_M}$
, respectively.
${I_M}$
, respectively.
3. Measuring the correlation function for maser sources. discussion
In contrast to the classical Hanbury Brown-Twiss experiment, in which the spatial correlation of intensity was measured in the optical range, for narrow-band radio sources it is possible to directly measure the degenerate normalised second-order autocorrelation function, that is, the bunching parameter
![]() $g_{11}^{(2)}$
can be determined by taking measurements at one point during some time. In the optical range, this would require a detector with a time resolution much less than one picosecond.
$g_{11}^{(2)}$
can be determined by taking measurements at one point during some time. In the optical range, this would require a detector with a time resolution much less than one picosecond.
Values of
![]() $g_{11}^{(2)}$
follow from Equations (5), (15), and (16), are
$g_{11}^{(2)}$
follow from Equations (5), (15), and (16), are
for the thermal radiation, and
for the maser radiation. When the conditions necessary for Equations (1) and (1a) are satisfied, the radiation power recorded by the radio telescope is proportional to the radiation intensity. So, the intensity
![]() $I$
in all equations below can be replaced by the recorded power of the radio source
$I$
in all equations below can be replaced by the recorded power of the radio source
![]() $P$
. Therefore, the bunching parameter is determined by the mean square of the power
$P$
. Therefore, the bunching parameter is determined by the mean square of the power
![]() $\left\langle {{P^2}} \right\rangle $
and the variance of the squared power
$\left\langle {{P^2}} \right\rangle $
and the variance of the squared power
![]() $\left\langle {\Delta {P^2}} \right\rangle $
$\left\langle {\Delta {P^2}} \right\rangle $
Determination of this parameter provides an opportunity to clarify the nature of radiation from the objects that are considered as astrophysical masers. The resulting value
![]() $g_{11}^{(2)} \lt 2$
will indicate the non-thermal (maser) nature of the source.
$g_{11}^{(2)} \lt 2$
will indicate the non-thermal (maser) nature of the source.
To assess the possibility of determining
![]() $g_{11}^{(2)}$
, let us consider the order of the quantities included in formulas (6)–(10) for masers on molecules
$g_{11}^{(2)}$
, let us consider the order of the quantities included in formulas (6)–(10) for masers on molecules
![]() $OH$
(
$OH$
(
![]() $\lambda = 18$
cm) and
$\lambda = 18$
cm) and
![]() ${H_2}O$
(
${H_2}O$
(
![]() $\lambda = 1.35$
cm). Assuming for estimates of
$\lambda = 1.35$
cm). Assuming for estimates of
![]() $\Delta \theta = 2 \cdot {10^{ - 2}}$
s,
$\Delta \theta = 2 \cdot {10^{ - 2}}$
s,
![]() $\Delta \nu \approx $
0.7 km s–1
$\Delta \nu \approx $
0.7 km s–1
![]() $ \approx 4$
KHz for
$ \approx 4$
KHz for
![]() $OH$
-masers (Patoka et al. Reference Patoka2021; Clegg & Cordes Reference Clegg and Cordes1991), we obtain the following values:
$OH$
-masers (Patoka et al. Reference Patoka2021; Clegg & Cordes Reference Clegg and Cordes1991), we obtain the following values:
the coherence time is
![]() ${t_{coh}} \approx $
250 µs,
${t_{coh}} \approx $
250 µs,
the longitudinal coherence length is
![]() $c{t_{coh}} \approx $
75 km,
$c{t_{coh}} \approx $
75 km,
the spatial coherence radius is
![]() ${\rho _{coh}} \approx 1.8 \cdot {10^3}$
km for
${\rho _{coh}} \approx 1.8 \cdot {10^3}$
km for
![]() $OH$
maser,
$OH$
maser,
![]() ${\rho _{coh}} \approx 135$
km for
${\rho _{coh}} \approx 135$
km for
![]() ${H_2}O$
maser.
${H_2}O$
maser.
The values of the longitudinal coherence length and the spatial coherence radius are many times larger than the size of the radio telescope antenna, and Equation (10) is satisfied. The situation concerning the temporal resolution is more complicated. According to Equation (1a), see also Equation (20), the hardware should provide significantly better temporal resolution than the reverse bandwidth or, equivalently, the coherence time. For a maser, the temporal resolution should be 10 µs or less. Such temporal resolution is not required for routine observations of masers. Recently, however, equipment used to study pulsars and fast radio bursts has appeared, which has the required resolution (Bij Reference Bij2021; Nimmo Reference Nimmo2021). Apparently, the use of such or similar equipment makes it possible to experimentally measure the bunching parameter of masers.
The determination procedure consists from the long-time measurement of the radiation power of the source with a time resolution
![]() $\tau \lt\lt {t_{coh}} = {\left( {\Delta \nu } \right)^{ - 1}}$
, and the determination of the value of
$\tau \lt\lt {t_{coh}} = {\left( {\Delta \nu } \right)^{ - 1}}$
, and the determination of the value of
![]() $g_{11}^{(2)}$
by further statistical processing of the received data. According to Equations (17)–(19), the processing includes determination of the mean square of the radiation power and the square of the mean radiation power, or, equivalently, the determination of the square of the mean radiation power and the dispersion of the square of the power. To ensure the averaging, the value of the limiting temporal resolution should be at least two orders of magnitude greater than the value of the reciprocal radiation frequency. In other words, the bandwidth should be much less than the radiation frequency,
$g_{11}^{(2)}$
by further statistical processing of the received data. According to Equations (17)–(19), the processing includes determination of the mean square of the radiation power and the square of the mean radiation power, or, equivalently, the determination of the square of the mean radiation power and the dispersion of the square of the power. To ensure the averaging, the value of the limiting temporal resolution should be at least two orders of magnitude greater than the value of the reciprocal radiation frequency. In other words, the bandwidth should be much less than the radiation frequency,
![]() $B \lt\lt \nu $
. Thus, the condition for the bandwidth takes the form
$B \lt\lt \nu $
. Thus, the condition for the bandwidth takes the form
This relation coincides with Equation (1a).
Uncertainty
![]() $\delta g$
of the value
$\delta g$
of the value
![]() $g_{11}^{(2)}$
, which is crucial for determining the nature of the radiation, depends on the errors of the measured values
$g_{11}^{(2)}$
, which is crucial for determining the nature of the radiation, depends on the errors of the measured values
![]() ${\left\langle {{P^2}} \right\rangle _m}$
and
${\left\langle {{P^2}} \right\rangle _m}$
and
![]() $\left\langle P \right\rangle _m^2$
, which differ from the true values
$\left\langle P \right\rangle _m^2$
, which differ from the true values
![]() $\left\langle {{P^2}} \right\rangle $
and
$\left\langle {{P^2}} \right\rangle $
and
![]() ${\left\langle P \right\rangle ^2}$
. In a continuous measurement process, their accuracy is determined by the product
${\left\langle P \right\rangle ^2}$
. In a continuous measurement process, their accuracy is determined by the product
![]() $BT$
of the duration of measurements
$BT$
of the duration of measurements
![]() $T$
and the bandwidth
$T$
and the bandwidth
![]() $B$
. If measurements are made discretely, then their number
$B$
. If measurements are made discretely, then their number
![]() $N$
provides the same accuracy as the value of
$N$
provides the same accuracy as the value of
![]() $BT$
for continuous measurements, provided (Bendat & Piersol Reference Bendat and Piersol2010)
$BT$
for continuous measurements, provided (Bendat & Piersol Reference Bendat and Piersol2010)
Based on Equation (19), uncertainty
![]() $\delta g$
of the bunching parameter
$\delta g$
of the bunching parameter
![]() $g_{11}^{(2)}$
is calculated as (Bendat & Piersol Reference Bendat and Piersol2010)
$g_{11}^{(2)}$
is calculated as (Bendat & Piersol Reference Bendat and Piersol2010)
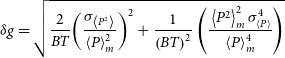 \begin{align}\delta g = \sqrt {\frac{2}{{BT}}{{\left( {\frac{{{\sigma _{\left\langle {{P^2}} \right\rangle }}}}{{\left\langle P \right\rangle _m^2}}} \right)}^2} + \frac{1}{{{{\left( {BT} \right)}^2}}}\left( {\frac{{\;\left\langle {{P^2}} \right\rangle _m^2\sigma _{\left\langle P \right\rangle }^4}}{{\left\langle P \right\rangle _m^4}}} \right)} \end{align}
\begin{align}\delta g = \sqrt {\frac{2}{{BT}}{{\left( {\frac{{{\sigma _{\left\langle {{P^2}} \right\rangle }}}}{{\left\langle P \right\rangle _m^2}}} \right)}^2} + \frac{1}{{{{\left( {BT} \right)}^2}}}\left( {\frac{{\;\left\langle {{P^2}} \right\rangle _m^2\sigma _{\left\langle P \right\rangle }^4}}{{\left\langle P \right\rangle _m^4}}} \right)} \end{align}
Here,
![]() ${\sigma _{\left\langle {{P^2}} \right\rangle }}$
and
${\sigma _{\left\langle {{P^2}} \right\rangle }}$
and
![]() ${\sigma _{\left\langle P \right\rangle }}$
are the variances of the measured values
${\sigma _{\left\langle P \right\rangle }}$
are the variances of the measured values
![]() ${\left\langle {{P^2}} \right\rangle _m}$
and
${\left\langle {{P^2}} \right\rangle _m}$
and
![]() $\left\langle P \right\rangle _m^2$
(not to be confused with the variance determined by relation (3)). Obviously, the factors in parentheses in relation (22) are of order of 1. In addition, for large values of the product
$\left\langle P \right\rangle _m^2$
(not to be confused with the variance determined by relation (3)). Obviously, the factors in parentheses in relation (22) are of order of 1. In addition, for large values of the product
![]() $BT$
, the second term is negligible compared to the first one. Thus, with a bandwidth
$BT$
, the second term is negligible compared to the first one. Thus, with a bandwidth
![]() $B$
= 10 MHz, the duration
$B$
= 10 MHz, the duration
![]() $T$
of the measurement process more than a few seconds provides a fairly good accuracy in determining the value of
$T$
of the measurement process more than a few seconds provides a fairly good accuracy in determining the value of
![]() $g_{11}^{(2)}$
.
$g_{11}^{(2)}$
.
Hardware noise also affects the accuracy of the determination. The accuracy of determining of
![]() $g_{11}^{(2)}$
can be improved in the case of registering not only the total power
$g_{11}^{(2)}$
can be improved in the case of registering not only the total power
![]() ${P_0}$
, which is the sum of the useful signal
${P_0}$
, which is the sum of the useful signal
![]() $P$
and noise
$P$
and noise
![]() ${P_1}$
, but also the noise separately. If
${P_1}$
, but also the noise separately. If
![]() $P$
and
$P$
and
![]() ${P_1}$
are statistically independent, the mean value of the total power is the sum of the mean values of the mean value of the signal power and the mean value of the noise power
${P_1}$
are statistically independent, the mean value of the total power is the sum of the mean values of the mean value of the signal power and the mean value of the noise power
and the total variance is the sum of variances
From this it follows that
![]() $g_{11}^{(2)}$
can be presented as
$g_{11}^{(2)}$
can be presented as
Assuming that the values of
![]() $\left\langle {P_1^2} \right\rangle - {\left\langle {{P_1}} \right\rangle ^2}$
and
$\left\langle {P_1^2} \right\rangle - {\left\langle {{P_1}} \right\rangle ^2}$
and
![]() $\left\langle {{P_1}} \right\rangle $
are known with enough accuracy for a radio telescope, the uncertainty
$\left\langle {{P_1}} \right\rangle $
are known with enough accuracy for a radio telescope, the uncertainty
![]() $\delta g$
of the bunching parameter
$\delta g$
of the bunching parameter
![]() $g_{11}^{(2)}$
in this case is equal to (Bendat & Piersol Reference Bendat and Piersol2010)
$g_{11}^{(2)}$
in this case is equal to (Bendat & Piersol Reference Bendat and Piersol2010)
 \begin{align}\delta g & = \frac{1}{{{{\left( {\left\langle {{P_0}} \right\rangle - \left\langle {{P_1}} \right\rangle } \right)}^2}}}\nonumber\\[5pt]
& \quad \times \sqrt {\frac{{2{{\left( {{\sigma _{\left\langle {P_0^2} \right\rangle }}} \right)}^2}}}{{BT}} + \frac{{\sigma _{\left\langle {{P_0}} \right\rangle }^4{{\left( {\left\langle {{P_0}} \right\rangle \left\langle {{P_1}} \right\rangle - {{\left\langle {{P_0}} \right\rangle }^2} + \left\langle {P_1^2} \right\rangle - {{\left\langle {{P_1}} \right\rangle }^2}} \right)}^2}}}{{{{\left( {BT} \right)}^2}{{\left( {\left\langle {{P_0}} \right\rangle - \left\langle {{P_1}} \right\rangle } \right)}^2}{{\left\langle {{P_0}} \right\rangle }^2}}}} \end{align}
\begin{align}\delta g & = \frac{1}{{{{\left( {\left\langle {{P_0}} \right\rangle - \left\langle {{P_1}} \right\rangle } \right)}^2}}}\nonumber\\[5pt]
& \quad \times \sqrt {\frac{{2{{\left( {{\sigma _{\left\langle {P_0^2} \right\rangle }}} \right)}^2}}}{{BT}} + \frac{{\sigma _{\left\langle {{P_0}} \right\rangle }^4{{\left( {\left\langle {{P_0}} \right\rangle \left\langle {{P_1}} \right\rangle - {{\left\langle {{P_0}} \right\rangle }^2} + \left\langle {P_1^2} \right\rangle - {{\left\langle {{P_1}} \right\rangle }^2}} \right)}^2}}}{{{{\left( {BT} \right)}^2}{{\left( {\left\langle {{P_0}} \right\rangle - \left\langle {{P_1}} \right\rangle } \right)}^2}{{\left\langle {{P_0}} \right\rangle }^2}}}} \end{align}
and can also be quite small for a large value of the product
![]() $BT$
.
$BT$
.
Acknowledgments
The author is grateful to G. Kh. Kitaeva and A. N. Milovidov for the help in preparing this work, and S. V. Kalenckii for providing the useful information.
Data availability
The data that support the findings of this study are available within this paper and from the author upon reasonable request.



