Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-18T05:26:35.036Z Has data issue: false hasContentIssue false
  • English
  • Français

The Influence of the Rayleigh and Prandtl Numbers on Convective Heat Transport in Stars

Published online by Cambridge University Press:  25 April 2016

J. O. Murphy
J. O. Murphy*
Affiliation:
Department of Mathematics, Monash University
Get access Rights & Permissions [Opens in a new window]

Extract

The two important parameters which essentially determine the nature of the convective regime, and consequently the total heat transported by convective processes, across an unstable layer in a star are the Rayleigh and Prandtl numbers defined by (Chandrasekhar 1961)

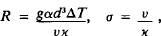
where ν is the coefficient of kinematic viscosity, x is the coefficient of thermal diffusivity and α, g, d, ΔT are respectively the coefficient of thermal expansion, acceleration due to gravity, depth of the fluid layer and temperature difference across the layer. In addition, the horizontal scale of the convection cell is determined by the horizontal wave number a and for convection to be established R must be greater than the critical value at marginal stability, Rc, which is a function of a, given by

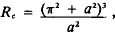
when the free boundary conditions apply.

Type
Contributions
Information
Publications of the Astronomical Society of Australia , Volume 4 , Issue 1 , 1980 , pp. 39 - 41
Copyright
Copyright © Astronomical Society of Australia 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Böhm, K. H., I.A.U. Col. No. 53 (In Press) (1979).Google Scholar
Böhm, K. H., Carson, J. R., Fontaine, G., and Van Horn, H. M., Astrophys. J. 217, 521 (1977).Google Scholar
Böhm, K. H., and Cassinelli, J., Astron. Astrophys., 12, 21 (1971).Google Scholar
Chandrasekhar, S., Hydromagnetic and Hydrodynamic Stability, Clarendon Press: Oxford (1961).Google Scholar
Gough, D. O., Speigel, E. A., and Toomre, J., J. Fluid Mech., 68, 719 (1975).Google Scholar
Roberts, P. H., In Non-equilibrium Thermodynamics, Variational Techniques and Stability (Eds. Donnelly, R. J., Herman, R., and Prigogine, I.). Chicago Univ. Press, 125 (1966).Google Scholar
Speigel, E. A., Convection in Stars — Part I, Annu. Rev. Astr. Astrophys., 9, 323 (1971).Google Scholar
Van der Borght, R., Pubis., Astr. Soc., Japan, 23, 539 (1971).Google Scholar