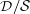1. Introduction
With the advent of new facilities, radio surveys are becoming larger and deeper, providing fields rich in sources, in the tens of millions (Norris Reference Norris2017), and delivering data at increasing rates, in the hundreds of gigabytes per second (Whiting & Humphreys Reference Whiting and Humphreys2012). The Evolutionary Map of the Universe (EMU, Norris et al. Reference Norris2011, Reference Norris2021) is expected to detect up to 40 million sources, expanding our knowledge in areas such as galaxy evolution and star formation. This outstrips surveys like the Karl G. Jansky Very Large Array (JVLA, or VLA) Sky Survey (VLASS, Lacy et al. Reference Lacy2020; Gordon et al. Reference Gordon2021) and the Rapid Australian Square Kilometre Array (SKA) Pathfinder (ASKAP) Continuum Survey (RACS, McConnell et al. Reference McConnell2020; Hale et al. Reference Hale2021) by a factor of up to 30. Furthermore, the Variable and Slow Transients (VAST, Banyer et al., Reference Banyer, Murphy, VAST, Ballester, Egret and Lorente2012; Murphy et al., Reference Murphy2013, Reference Murphy2021) survey, operating at a cadence of 5s, surpasses VLASS transient studies by several orders of magnitude, opening up areas of variable and transient research: e.g., flare stars, intermittent pulsars, X-ray binaries, magnetars, extreme scattering events, interstellar scintillation, radio supernovae, and orphan afterglows of gamma-ray bursts (Murphy et al., Reference Murphy2013, Reference Murphy2021). This places complex requirements on source finder (SF) software in order to reliably handle compact,Footnote a extended, complex, and faint or diffuse sources, along with demands for high data throughput for radio transients (e.g., Hancock et al., Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012; Hopkins et al., Reference Hopkins2015; Riggi et al., Reference Riggi2016; Hale et al., Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019; Boyce, Reference Boyce2020; Bonaldi et al., Reference Bonaldi2021). No current SF fits all of these requirements.
Hydra is an attempt to get the best of all worlds: it is an extensible multi-SF comparison and cataloguing tool, which allows users to choose the appropriate SF for a given survey, or take advantage of its collectively rich statistics by combining results. The Hydra software suiteFootnote b currently includes Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012; Hancock, Cathryn, & Hurley-Walker Reference Hancock, Cathryn and Hurley-Walker2018), Caesar (Compact And Extend Source Automated Recognition, Riggi et al. Reference Riggi2016, Reference Riggi2019), ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), PyBDSF (Python Blob Detector and Source Finder, Mohan & Rafferty Reference Mohan and Rafferty2015), and Selavy (Whiting & Humphreys Reference Whiting and Humphreys2012).
This paper is part one of a two part series, (referred to hereafter as Papers I and II). Here we provide a brief overview of SFs, relevant to our implementation of Hydra. This is then followed by a description of the Hydra software suite. The software produces new metrics for handling real source components (or sources, herein), such as, completeness (
![]() $\mathcal{C}$
) and reliability (
$\mathcal{C}$
) and reliability (
![]() $\mathcal{R}$
), based on sources detected in a shallow (
$\mathcal{R}$
), based on sources detected in a shallow (
![]() $\mathcal{S}$
) image (e.g., a real image with artificial noise added) wherein real (sometimes referred to as ‘deep’ or
$\mathcal{S}$
) image (e.g., a real image with artificial noise added) wherein real (sometimes referred to as ‘deep’ or
![]() $\mathcal{D}$
) image detections are considered as true sources. We use simulated data, where the true sources are known, to validate these metrics. In Paper II we use the simulated images along with real data to evaluate the performance of the six different SFs included with Hydra. A preliminary discussion on SF performance is presented in this paper.
$\mathcal{D}$
) image detections are considered as true sources. We use simulated data, where the true sources are known, to validate these metrics. In Paper II we use the simulated images along with real data to evaluate the performance of the six different SFs included with Hydra. A preliminary discussion on SF performance is presented in this paper.
2. Source finders
The growing sizes and data rates of modern radio surveys have increased the need for automated source finding tools with fast processing speeds, and high completeness and reliability. One impetus for this came through the ASKAP EMU source finding data challenge (Hopkins et al. Reference Hopkins2015), which explored a community-submitted set of eleven SFs: Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012), Astronomical Point source EXtractor (APEX, Makovoz & Marleau Reference Makovoz and Marleau2005), blobcat (Hales et al. Reference Hales, Murphy, Curran, Middelberg, Gaensler and Norris2012), Curvature Threshold Extractor (CuTEx, Molinari et al. Reference Molinari, Schisano, Faustini, Pestalozzi, di Giorgio and Liu2011), Duchamp (Whiting Reference Whiting2012), IFCA (International Federation of Automation Control) Biparametric Adaptive Filter (BAF, López-Caniego & Vielva Reference López-Caniego and Vielva2012)/Matched Filter (MF, López-Caniego et al. Reference López-Caniego, Herranz, González-Nuevo, Sanz, Barreiro, Vielva, Argüeso and Toffolatti2006), PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), Python Source Extractor (PySE, Spreeuw Reference Spreeuw2010; Swinbank et al. Reference Swinbank2015), Search and Destroy (SAD, Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998, with an honourable mention of its variant HAPPY, White et al. Reference White, Becker, Helfand and Gregg1997), Selavy (with Duchamp at its core, Whiting & Humphreys Reference Whiting and Humphreys2012), Source Extractor (SExtractor, Bertin & Arnouts Reference Bertin and Arnouts1996), and SOURCE_FIND (Arcminute Microkelvin Imager (AMI) pipeline, AMI Consortium: Franzen et al. 2011). More recent SFs include Caesar (Riggi et al. Reference Riggi2016, Reference Riggi2019) and ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019; Boyce Reference Boyce2020). APEX, CuTEx, ProFound, and SExtractor have their origins in optical astronomy. Our focus will be on 2D SFs, such as those above, although there are also 3D packages like SoFiA (Source Finding Application, Serra et al. Reference Serra2015; Koribalski et al. Reference Koribalski2020; Westmeier et al. Reference Westmeier2021) optimised for detecting line emission in data cubes, which can also function as 2D SFs.
By and large there is no ‘one SF fits all’ solution. Each is typically optimised for specific tasks (Hopkins et al. Reference Hopkins2015; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019; Bonaldi et al. Reference Bonaldi2021). In the broadest sense, there are SFs designed to handle sources that are compact, or extended and diffuse, see Table 1. They also have their specialisations: for example, blobcat for linear polarisation data (Hales et al. Reference Hales, Murphy, Curran, Middelberg, Gaensler and Norris2012), Duchamp for HI observations (Whiting Reference Whiting2012), CuTEx for images with intense background fluctuations (Molinari et al. Reference Molinari, Schisano, Faustini, Pestalozzi, di Giorgio and Liu2011), and PySE for transients (Fender et al. Reference Fender2007; van Haarlem et al. Reference van Haarlem2013). There are also ‘Next Generation’ (NxGen) SFs (see Table 1), which utilise multiple processors for handling high data throughput (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012; Riggi et al. Reference Riggi2016; Whiting & Humphreys Reference Whiting and Humphreys2012). Qualitatively different types of source finding and characterisation tools are being developed that use machine learning approaches (e.g., Bonaldi et al. Reference Bonaldi2021; Lao et al. Reference Lao, An, Wang, Xu, Guo, Lv, Wu and Zhang2021; D. Magro et al., in preparation), as well as citizen science approaches to classifying radio sources (e.g., Banfield et al. Reference Banfield2015; Alger et al. Reference Alger2018), although it is beyond the scope of Hydra to attempt to incorporate all such efforts.
Table 1. SF general design characteristics (re., Hopkins et al. Reference Hopkins2015; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019; Bonaldi et al. Reference Bonaldi2021). NxGen indicates multiprocessing capabilities.

![]() $^{\rm a}$
Optical SF.
$^{\rm a}$
Optical SF.
In general, SFs typically analyse an image in 3 stages: (1) background and noise estimation, (2) island detection, and (3) component modelling.
For the background estimation most SFs used in radio astronomy such as Aegean, PyBDSF, and Selavy, tend to use a sliding box method, where background noise estimates are calculated at a specific location using neighbouring pixels within a given box size, and estimated again for adjacent locations based on the sliding-step size. It is important that the box size be set so as not to be too small around bright sources, which would overestimate the background noise, or too large, so as to wash out any varying background structure that is important for reliable detection of faint sources (e.g., Huynh et al Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012). This is discussed further below in Section 3.1.3.
Background noise estimation can be performed through various metrics such as the inter-quartile range (IQR) used by Aegean (with median background and IQR noise spread, Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012), mean background (
![]() $\mu$
) and RMS noise (
$\mu$
) and RMS noise (
![]() $\sigma$
) used by PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), or median background and Mean Absolute Deviation From the Median (MAD, or MADFM herein: e.g., Riggi et al. Reference Riggi2016; Hopkins et al. Reference Hopkins2015) noise used by Selavy (which also has a
$\sigma$
) used by PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), or median background and Mean Absolute Deviation From the Median (MAD, or MADFM herein: e.g., Riggi et al. Reference Riggi2016; Hopkins et al. Reference Hopkins2015) noise used by Selavy (which also has a
![]() $\mu$
/
$\mu$
/
![]() $\sigma$
option, Whiting & Humphreys Reference Whiting and Humphreys2012). SExtractor, on the other hand, uses
$\sigma$
option, Whiting & Humphreys Reference Whiting and Humphreys2012). SExtractor, on the other hand, uses
![]() $\kappa.\sigma$
-clipping and mode estimation (see Section 3.1.1; Da Costa Reference Da Costa and Howell1992; Bertin & Arnouts Reference Bertin and Arnouts1996; Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012; Akhlaghi & Ichikawa Reference Akhlaghi and Ichikawa2015; Riggi et al. Reference Riggi2016) over the entire image; while PySE performs
$\kappa.\sigma$
-clipping and mode estimation (see Section 3.1.1; Da Costa Reference Da Costa and Howell1992; Bertin & Arnouts Reference Bertin and Arnouts1996; Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012; Akhlaghi & Ichikawa Reference Akhlaghi and Ichikawa2015; Riggi et al. Reference Riggi2016) over the entire image; while PySE performs
![]() $\sigma$
-clipping locally (see Hopkins et al. Reference Hopkins2015). ProFound, an optical SF shown to be useful for radio images (Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), also uses a
$\sigma$
-clipping locally (see Hopkins et al. Reference Hopkins2015). ProFound, an optical SF shown to be useful for radio images (Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), also uses a
![]() $\sigma$
-clipping schema (via. the MakeSkyGrid routine, Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018) Caesar provides several options:
$\sigma$
-clipping schema (via. the MakeSkyGrid routine, Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018) Caesar provides several options:
![]() $\mu/\sigma$
, median/MADFM, biweight and
$\mu/\sigma$
, median/MADFM, biweight and
![]() $\sigma$
-clipped estimators (Riggi et al. Reference Riggi2016). The final stage typically involves bicubic interpolation to obtain the background noise estimates as a function of pixel location. It is important that these estimates are optimal as they have a significant effect on SF performance (Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012).
$\sigma$
-clipped estimators (Riggi et al. Reference Riggi2016). The final stage typically involves bicubic interpolation to obtain the background noise estimates as a function of pixel location. It is important that these estimates are optimal as they have a significant effect on SF performance (Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012).
There are various methods for island detection within an image. Perhaps the simplest is thresholding, in which the pixel with the highest flux is chosen along with neighbouring pixels down to some threshold above the background noise, defining an island. Variants of this method are used by Duchamp (Whiting & Humphreys Reference Whiting and Humphreys2012), ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018), Selavy (Whiting Reference Whiting2012), and SExtractor (Bertin & Arnouts Reference Bertin and Arnouts1996). Once the initial set of islands are chosen, they are sometimes then grown down to a lower threshold according to certain rules. For instance, ProFound uses a Kron/Petrosian-like dilation kernel, that is, it uses an island-shaped aperture (Kron Reference Kron1980; Petrosian Reference Petrosian1976) to grow the islands according to a surface brightness profile, in an iterative process, until the desired profile or lower threshold limit is reached (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018). It then separates out the islands into segments, through a watershed deblending technique.Footnote c Another method is flood-fill, wherein islands are seeded above some threshold and then grown down to a lower threshold, according to a set of rules. Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012), blobcat (Hales et al. Reference Hales, Murphy, Curran, Middelberg, Gaensler and Norris2012), Caesar (Riggi et al. Reference Riggi2016), PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), and PySE (Swinbank et al. Reference Swinbank2015) use variations on this theme.
The component extraction phase is perhaps the most varied in terms of modelling. The simplest is the top down raster-scan within an island to find flux peaks given some step size, or tolerance level. This method is utilised by Duchamp (Whiting & Humphreys Reference Whiting and Humphreys2012), and, in turn, is also employed by Selavy. These peaks are then fitted by elliptical Gaussians producing a component catalogue. The choice of elliptical Gaussians is motivated by the fact that point sources, or sources that are only very slightly extended, are well-modelled in this way as it corresponds to the shape of the telescope’s synthesised beam. More complex source structures, on the other hand, tend to be poorly fit by this choice, leading to variations in fitting approach. Some SFs, for example, use multiple Gaussians to fit to an island, using various criteria. PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015) and PySE (Spreeuw Reference Spreeuw2010; Swinbank et al. Reference Swinbank2015) fall into this category.
There are also a class of SFs that use curvature maps to determine radio source components. Aegean searches for local maxima within an island which in turn are fitted by Gaussians, constrained by negative curvature valleys (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012). Caesar is rather unique in that it first searches for peaks and then uses watershed deblending to create sub-islands, for seeding and constraining Gaussian fits, respectively (Riggi et al. Reference Riggi2016). Extended sources are then extracted from the resulting residual image, using wavelet transform, saliency, hierarchical-clustering, or active-contour filtering. Consequently, Caesar is capable of extracting extended sources with complex structure.
The aforementioned SF algorithms are just the tip of the iceberg of possibilities (c.f., Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012; Hopkins et al. Reference Hopkins2015; Wu et al. Reference Wu2018; Lukic, de Gasperin, & Brüggen Reference Lukic, de Gasperin and Brüggen2019; Sadr et al. Reference Sadr, Vos, Bassett, Hosenie, Oozeer and Lochner2019; Bonaldi et al. Reference Bonaldi2021; D. Magro et al., in preparation). In our initial implementation of Hydra we have chosen to explore a representative set of commonly used SFs: Aegean, Caesar, ProFound, PyBDSF, and Selavy
3. Hydra
Hydra is a software tool capable of running multiple SFs. It is extensible, in that other SFs can be added in a containerised fashion by following a set of straightforward template-like rules. It provides diagnostic information such as
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{R}$
. Statistical analysis can be based on injected (
$\mathcal{R}$
. Statistical analysis can be based on injected (
![]() $\mathcal{J}$
) source catalogues from simulated images or on real
$\mathcal{J}$
) source catalogues from simulated images or on real
![]() $\mathcal{D}$
-images used as ground truths for detections in their
$\mathcal{D}$
-images used as ground truths for detections in their
![]() $\mathcal{S}$
counterparts. Hydra is innovative in that it minimises the False Detection Rate (FDR, Whiting Reference Whiting2012) of the SFs by adjusting their detection threshold and island growth (and optionally RMS box) parameters. This is an essential step in automation, especially when dealing with large surveys such as EMU (Norris Reference Norris2017; Norris et al. Reference Norris2021).
$\mathcal{S}$
counterparts. Hydra is innovative in that it minimises the False Detection Rate (FDR, Whiting Reference Whiting2012) of the SFs by adjusting their detection threshold and island growth (and optionally RMS box) parameters. This is an essential step in automation, especially when dealing with large surveys such as EMU (Norris Reference Norris2017; Norris et al. Reference Norris2021).
3.1. The hydra software suite
Upon Heracles shield wrought Homados (Tumult), the din of battle noise, and riding alongside Cerberus, the unruly master of mayhem. Only the wrath of Cerberus’s father Typhon, a controlling force, can temper their chaos. And hitherto, Typhon’s son Hydra, was tasked with bringing the chaos to bear fruit, while his mother Echidna, a hidden force, plucked the fruit from the vines to make wine. (Inspired from Reference Powell Powell, 2017 , and Reference Buxton Buxton, 2016 .)
Fig. 1 shows an overview of the Hydra software suite, which consists of the following software components: Homados, Cerberus, Typhon, and Hydra. Homados is used for providing image statistics such as
![]() $\mu/\sigma$
, and image manipulation such as inversion and adding noise. Cerberus is an extensible multi-SF software suite. It currently includes Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012, Reference Hancock, Cathryn and Hurley-Walker2018), Caesar (Riggi et al. Reference Riggi2016, Reference Riggi2019), ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), and Selavy (Whiting & Humphreys Reference Whiting and Humphreys2012). Typhon is a tool for optimising the SF parameters and then producing output catalogues. It uses Homados and Cerberus to do this task. Hydra is the main tool which uses Typhon to produce data products, including catalogues, residual images, and region files.Footnote d Echidna is a planned catalogue stacking and integration tool, to be added to Hydra.
$\mu/\sigma$
, and image manipulation such as inversion and adding noise. Cerberus is an extensible multi-SF software suite. It currently includes Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012, Reference Hancock, Cathryn and Hurley-Walker2018), Caesar (Riggi et al. Reference Riggi2016, Reference Riggi2019), ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), and Selavy (Whiting & Humphreys Reference Whiting and Humphreys2012). Typhon is a tool for optimising the SF parameters and then producing output catalogues. It uses Homados and Cerberus to do this task. Hydra is the main tool which uses Typhon to produce data products, including catalogues, residual images, and region files.Footnote d Echidna is a planned catalogue stacking and integration tool, to be added to Hydra.

Figure 1. High level schematic representation of the Hydra software suite workflow. Homados provides
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-image channels for simulated/real images (‘dancing ghosts’ example image, see Norris et al. Reference Norris2021). Each channel is run separately through the Typhon optimiser, which uses the SF interface provided by Cerberus. Hydra coordinates all of these activities, building catalogues and compiling statistics at the end of the process.
$\mathcal{S}$
-image channels for simulated/real images (‘dancing ghosts’ example image, see Norris et al. Reference Norris2021). Each channel is run separately through the Typhon optimiser, which uses the SF interface provided by Cerberus. Hydra coordinates all of these activities, building catalogues and compiling statistics at the end of the process.
3.1.1. Homados
The main purpose of Homados is to add noise to images. We shall often refer to the original image, as the
![]() $\mathcal{D}$
-image, and the noise-added image, as the
$\mathcal{D}$
-image, and the noise-added image, as the
![]() $\mathcal{S}$
-image. These ‘deep-shallow’ (
$\mathcal{S}$
-image. These ‘deep-shallow’ (
![]() $\mathcal{DS}$
) image pairs can be used to create statistics such as
$\mathcal{DS}$
) image pairs can be used to create statistics such as
![]() $\mathcal{DS}$
-completeness (
$\mathcal{DS}$
-completeness (
![]() $\mathcal{C_{DS}}$
) and
$\mathcal{C_{DS}}$
) and
![]() $\mathcal{DS}$
-reliability (
$\mathcal{DS}$
-reliability (
![]() $\mathcal{R_{DS}}$
), based on the assumption that the sources detected in the
$\mathcal{R_{DS}}$
), based on the assumption that the sources detected in the
![]() $\mathcal{D}$
-image are real. These statistics are used for real images, where the source inputs are unknown.
$\mathcal{D}$
-image are real. These statistics are used for real images, where the source inputs are unknown.
An
![]() $\mathcal{S}$
-image is created by adding to the
$\mathcal{S}$
-image is created by adding to the
![]() $\mathcal{D}$
-image a Gaussian noise map that has been convolved with the corresponding synthesised beam (i.e., BMIN, BMAJ, and BPA). The noise map is created with mean noise,
$\mathcal{D}$
-image a Gaussian noise map that has been convolved with the corresponding synthesised beam (i.e., BMIN, BMAJ, and BPA). The noise map is created with mean noise,
![]() $\mu_{image}$
, and RMS noise,
$\mu_{image}$
, and RMS noise,
![]() $n\sigma_{image}$
(
$n\sigma_{image}$
(
![]() $\equiv\sigma_{noise\;\;map}$
), where n is the desired noise level (i.e., factor), and
$\equiv\sigma_{noise\;\;map}$
), where n is the desired noise level (i.e., factor), and
![]() $\mu_{image}$
and
$\mu_{image}$
and
![]() $\sigma_{image}$
are obtained from the
$\sigma_{image}$
are obtained from the
![]() $\mathcal{D}$
-image using
$\mathcal{D}$
-image using
![]() $\sigma$
-clipping (Akhlaghi & Ichikawa Reference Akhlaghi and Ichikawa2015). This is then convolved with the synthesised beam, from which its RMS noise,
$\sigma$
-clipping (Akhlaghi & Ichikawa Reference Akhlaghi and Ichikawa2015). This is then convolved with the synthesised beam, from which its RMS noise,
![]() $\sigma_{convolved}$
, is computed. For convergence, this process is repeated using the convolved image as input, but with n replaced by
$\sigma_{convolved}$
, is computed. For convergence, this process is repeated using the convolved image as input, but with n replaced by
![]() $\sigma_{noise\;\;map}\,n/\sigma_{convolved}$
. The final convolved image is then added to the
$\sigma_{noise\;\;map}\,n/\sigma_{convolved}$
. The final convolved image is then added to the
![]() $\mathcal{D}$
-image, obtaining the
$\mathcal{D}$
-image, obtaining the
![]() $\mathcal{S}$
-image.
$\mathcal{S}$
-image.
Fig. 2 shows an example of an
![]() $\mathcal{S}$
-image generated by Homados from an Australia Telescope Large Area Survey (ATLAS) Chandra Deep Field South (CDFS) Data Release 1 (DR1) tile (Norris et al. Reference Norris2006). The noise level was scaled by a factor of
$\mathcal{S}$
-image generated by Homados from an Australia Telescope Large Area Survey (ATLAS) Chandra Deep Field South (CDFS) Data Release 1 (DR1) tile (Norris et al. Reference Norris2006). The noise level was scaled by a factor of
![]() $n=5$
. This factor is assumed for the
$n=5$
. This factor is assumed for the
![]() $\mathcal{S}$
-image generation in the rest of this paper.
$\mathcal{S}$
-image generation in the rest of this paper.

Figure 2. Homados
![]() $\mathcal{S}$
-image generation example, using an image cutout sample from an ATLAS CDFS DR1
$\mathcal{S}$
-image generation example, using an image cutout sample from an ATLAS CDFS DR1
![]() $2.2^{\circ}\times2.7^{\circ}$
tile (Norris et al. Reference Norris2006). The figures show
$2.2^{\circ}\times2.7^{\circ}$
tile (Norris et al. Reference Norris2006). The figures show
![]() $\mathcal{D}$
(left) and
$\mathcal{D}$
(left) and
![]() $\mathcal{S}$
(right) images, zoomed in. The noise level scale factor, n, was set to 5 to generate the shallow image.
$\mathcal{S}$
(right) images, zoomed in. The noise level scale factor, n, was set to 5 to generate the shallow image.
In addition, Homados uses
![]() $\sigma$
-clipping to compute image statistics, such as, m (median),
$\sigma$
-clipping to compute image statistics, such as, m (median),
![]() $\mu$
(mean),
$\mu$
(mean),
![]() $\sigma$
(RMS),
$\sigma$
(RMS),
![]() $I_{\min}$
(minimum pixel value), and
$I_{\min}$
(minimum pixel value), and
![]() $I_{\max}$
(maximum pixel value). It also does image inversion for FDR calculations.
$I_{\max}$
(maximum pixel value). It also does image inversion for FDR calculations.
3.1.2. Cerberus
Cerberus is an extensible interface for running SF modules within the Hydra software suite. It currently supports Aegean, Caesar, ProFound, PyBDSF, and Selavy, as indicated by its command-line interface.Footnote e
Table 2. Cerberus RMS and Island parameter definitions in units of
![]() $\sigma$
with respect to the background, with soft constraint
$\sigma$
with respect to the background, with soft constraint
![]() $\sigma_{Island}<\sigma_{RMS}$
.
$\sigma_{Island}<\sigma_{RMS}$
.

![]() $^{\rm a}$
https://github.com/PaulHancock/Aegean/wiki/Simple-usage.
$^{\rm a}$
https://github.com/PaulHancock/Aegean/wiki/Simple-usage.
![]() $^{\rm b}$
https://caesar-doc.readthedocs.io/en/latest/usage/app_options.html#input-options.
$^{\rm b}$
https://caesar-doc.readthedocs.io/en/latest/usage/app_options.html#input-options.
![]() $^{\rm c}$
https://cran.r-project.org/web/packages/ProFound/ProFound.pdf.
$^{\rm c}$
https://cran.r-project.org/web/packages/ProFound/ProFound.pdf.
![]() $^{\rm d}$
https://pybdsf.readthedocs.io/en/latest/process_image.html.
$^{\rm d}$
https://pybdsf.readthedocs.io/en/latest/process_image.html.
![]() $^{\rm e}$
https://www.atnf.csiro.au/computing/software/askapsoft/sdp/docs/current/analysis/selavy.html.
$^{\rm e}$
https://www.atnf.csiro.au/computing/software/askapsoft/sdp/docs/current/analysis/selavy.html.


New modules are added through code generation, using Jinja template-codeFootnote f in conjunction with DockerFootnote g and YAMLFootnote h configuration files. The workflow is as follows:
• Create a containerised SF wrapper:
– Create a SF wrapper script
– Create a Docker build file wrapper
– Update the master docker-compose build file
– Build the container image
• Update the cerberus.py script:
– Create a YAML metadata file
– Update the master YAML metadata file
– Run the Jinja script generator tool
• Test the Hydra software suite
• Update the GitFootnote i repository

Figure 3. Cerberus code generation workflow.
Fig. 3 summarises this high-level workflow: containers for each SF are shown under Container Images and the Docker and YAML configuration files are shown under Configuration Management. The developer must follow a fixed set of rules when adding a new SF, in order for the Jinja template-driven script generator to update Cerberus. (For the purpose of reproducibility, Appendix A provides architectural design notes, using Aegean as an example.) All of this is transparent to the user, who has access to a simple interface, so one does not have to be an expert at using SFs in order to use Hydra.
Hydra’s modular design requires that the user has access to the key elements of a SF’s interface; in particular, access to its ‘RMS-like’ and ‘Island-like’ parameters. In the case of Aegean, for example, this would be seedclip and floodclip (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012), respectively. It is important to note that the parameters are not necessarily equivalent between SFs;Footnote j regardless, they do affect thresholding and island formation. Consequently, they have the strongest influence on FDR calculations. Table 2 summarises the parameters for the currently supported SFs. These parameters are used by Typhon to baseline the SFs, by minimising their FDRs.
Hydra also requires that SF modules provide optional RMS box and step size parameters, even if they are dummies. Some SF software manuals recommend these parameters be externally optimised, under certain conditions. PyBDSF is an example of such a case.Footnote k Regardless, this is also a good way of baselining (i.e., calibrating, Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012; Riggi et al. Reference Riggi2016) SFs for comparison purposes.
3.1.3. Typhon
Typhon is a tool for optimising the SFs to a standard baseline that can be used for comparison purposes. We have adopted the Percent Real Detections (PRD) metric, as used by Hale et al. (Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019) in a comparative study of Aegean, ProFound, and PyBDSF: that is,
where
![]() $N_{image}$
is the number of detections in the original image, and
$N_{image}$
is the number of detections in the original image, and
![]() $N_{inv.\;image}$
is the number of detections in the inverted image.Footnote l Basically, if one assumes the image noise is predominately Gaussian, then the peaks detected in the inverted image should statistically match the noise-peaks detected in the non-inverted image. Thus the FDR can be reduced by optimising the PRD. This approach is not suitable for non-Gaussian (or non-symmetric) noise properties, such as the Ricean noise distribution in polarisation images.
$N_{inv.\;image}$
is the number of detections in the inverted image.Footnote l Basically, if one assumes the image noise is predominately Gaussian, then the peaks detected in the inverted image should statistically match the noise-peaks detected in the non-inverted image. Thus the FDR can be reduced by optimising the PRD. This approach is not suitable for non-Gaussian (or non-symmetric) noise properties, such as the Ricean noise distribution in polarisation images.

Figure 4. Example Typhon PRD of a
![]() $2^\circ\times2^\circ$
simulated
$2^\circ\times2^\circ$
simulated
![]() $\mathcal{D}$
-image (left) and its corresponding
$\mathcal{D}$
-image (left) and its corresponding
![]() $\mathcal{S}$
-image (right). The variation in the PRD with the RMS parameters (in
$\mathcal{S}$
-image (right). The variation in the PRD with the RMS parameters (in
![]() $\sigma$
units) is represented along the horizontal axis, and the variation in the PRD with the island parameters is represented by the error bars. The data points represent average values: that is, Aegean and ProFound indicate the true shape of the curves, due their insensitivity to their island parameters. The SF parameters are listed in Table 2. The dotted horizontal lines indicate the 90% PRD levels.
$\sigma$
units) is represented along the horizontal axis, and the variation in the PRD with the island parameters is represented by the error bars. The data points represent average values: that is, Aegean and ProFound indicate the true shape of the curves, due their insensitivity to their island parameters. The SF parameters are listed in Table 2. The dotted horizontal lines indicate the 90% PRD levels.
Typhon uses the RMS and island parameters to optimise the PRD for each SF. Fig. 4 shows Typhon generated PRD curves for a
![]() $2^\circ\times2^\circ$
simulated
$2^\circ\times2^\circ$
simulated
![]() $\mathcal{D}$
-image along with its corresponding
$\mathcal{D}$
-image along with its corresponding
![]() $\mathcal{S}$
-image. Typhon identifies the optimal parameters to be those that correspond to the 90% PRD threshold. This threshold is motivated by the desire to use the knee of the PRD curve, whose position appears to be scale-invariant above a certain image size. Although the shape of the curve is not always guaranteed to be smooth, this crude method appears to be quite effective at framing the region of interest around the desired 90% PRD. The 90% to 98% PRD range has been investigated and the former threshold seems to provide reasonable results. Hale et al. (Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019) use a 98% PRD to baseline their SFs, beyond which the detection rate degrades. At that cut-off, however, we tend to find a non-scale-invariant increase in the RMS threshold with image size.
$\mathcal{S}$
-image. Typhon identifies the optimal parameters to be those that correspond to the 90% PRD threshold. This threshold is motivated by the desire to use the knee of the PRD curve, whose position appears to be scale-invariant above a certain image size. Although the shape of the curve is not always guaranteed to be smooth, this crude method appears to be quite effective at framing the region of interest around the desired 90% PRD. The 90% to 98% PRD range has been investigated and the former threshold seems to provide reasonable results. Hale et al. (Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019) use a 98% PRD to baseline their SFs, beyond which the detection rate degrades. At that cut-off, however, we tend to find a non-scale-invariant increase in the RMS threshold with image size.
Typhon uses the image statistics output from Homados to determine the RMS parameter range over which to optimise the PRD:
where
with
![]() $\mu$
,
$\mu$
,
![]() $\sigma$
, and
$\sigma$
, and
![]() $I_{\max}$
determined through
$I_{\max}$
determined through
![]() $\sigma$
-clipping (re. Section 3.1.1). The
$\sigma$
-clipping (re. Section 3.1.1). The
![]() $1.5\sigma$
lower limit is where the FDR starts to degrade. In general, Typhon samples the PRD from high values to low values in the RMS parameter, while varying the island parameter at each step, until the 90% threshold is reached.
$1.5\sigma$
lower limit is where the FDR starts to degrade. In general, Typhon samples the PRD from high values to low values in the RMS parameter, while varying the island parameter at each step, until the 90% threshold is reached.

Figure 5. Clustering Algorithm Infographic: The left panel shows the results of 3 hypothetical SFs (red, green, and gold). The middle panel shows the results after clustering, resulting in two clumps, assigned clump_id 1 (upper panel) and clump_id 2 (lower panel). A clump is defined through the spatial overlap between SF detections (i.e., components), in the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-images together. The components are numbered independently and can be associated with the clump they end up in. For instance, components 1, 2, and 3 are linked together in the
$\mathcal{S}$
-images together. The components are numbered independently and can be associated with the clump they end up in. For instance, components 1, 2, and 3 are linked together in the
![]() $\mathcal{D}$
-image, and, in addition, 1 overlaps with 6, and 3 overlaps with 8, 9, and 10 in the
$\mathcal{D}$
-image, and, in addition, 1 overlaps with 6, and 3 overlaps with 8, 9, and 10 in the
![]() $\mathcal{S}$
-image. Together this set of components populate clump_id 1. Similarly, clump_id 2 is composed of components 4, 5, and 7. Clumps are centred in the Hydra Viewer (Fig. 7), with unassociated components greyed out. The right panel shows the results after the clumps are decomposed into closest (i.e., overlapping centre-to-centre) matches between SFs, in the
$\mathcal{S}$
-image. Together this set of components populate clump_id 1. Similarly, clump_id 2 is composed of components 4, 5, and 7. Clumps are centred in the Hydra Viewer (Fig. 7), with unassociated components greyed out. The right panel shows the results after the clumps are decomposed into closest (i.e., overlapping centre-to-centre) matches between SFs, in the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-images, such that there is only one SF with a match in the
$\mathcal{S}$
-images, such that there is only one SF with a match in the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-images. These matched sets are assigned match_ids, with boxes enclosing the extremities of the components. The Hydra Viewer displays these numbers at the centre of the boxes (which are coloured differently here, for emphasis). So clump_id 1 contains match_id 1 = {1, 2, 6} and match_id 2 = {3, 8, 9, 10}, while clump_id 2 contains match_id 3 = {4, 5, 7}.
$\mathcal{S}$
-images. These matched sets are assigned match_ids, with boxes enclosing the extremities of the components. The Hydra Viewer displays these numbers at the centre of the boxes (which are coloured differently here, for emphasis). So clump_id 1 contains match_id 1 = {1, 2, 6} and match_id 2 = {3, 8, 9, 10}, while clump_id 2 contains match_id 3 = {4, 5, 7}.
The island parameters are SF-specific, and are typically defined over a finite range. Table 3 shows the parameter ranges used by Hydra, which are stored in its Configuration Management (Fig. 3). Typhon uses this information along with the constraint
![]() $\sigma_{island}<\sigma_{RMS}$
(otherwise,
$\sigma_{island}<\sigma_{RMS}$
(otherwise,
![]() $\sigma_{island}=0.999\,\sigma_{RMS}$
), as it searches the parameter space.
$\sigma_{island}=0.999\,\sigma_{RMS}$
), as it searches the parameter space.
Table 3. Configured island parameters.

Typhon will also perform an initial RMS box optimisation before optimising the PRD, if it is configured to do so. This is of particular importance for extended objects or around bright sources (Mohan & Rafferty Reference Mohan and Rafferty2015), especially for Gaussian-based extraction SFs such as Aegean, PyBDSF, and Selavy. Typhon uses Aegean’s background/noise image generation tool, bane (Hancock et al. Reference Hancock, Cathryn and Hurley-Walker2018), to search the RMS box size (box_size) and step size (step_size) parameter space,
 \begin{equation} \left.\begin{array}{c} \mbox{$\displaystyle3\le\frac{\mbox{box_size}}{[4(\texttt{BMAJ}+\texttt{BMIN})/2]}\le6$}\\[10pt] \mbox{$\displaystyle\frac{1}{4}\le\frac{\mbox{step_size}}{\mbox{box_size}}\le\frac{1}{2}$}\\ \end{array}\right\}\,,\end{equation}
\begin{equation} \left.\begin{array}{c} \mbox{$\displaystyle3\le\frac{\mbox{box_size}}{[4(\texttt{BMAJ}+\texttt{BMIN})/2]}\le6$}\\[10pt] \mbox{$\displaystyle\frac{1}{4}\le\frac{\mbox{step_size}}{\mbox{box_size}}\le\frac{1}{2}$}\\ \end{array}\right\}\,,\end{equation}
for the lowest background level,
![]() $\mu$
(c.f., Riggi et al. Reference Riggi2016). The
$\mu$
(c.f., Riggi et al. Reference Riggi2016). The
![]() $4(\texttt{BMAJ}+\texttt{BMIN})/2$
factor represents the bane default box size, where we assume a square box, for simplicity. The limits 3 and 6 are consistent with the rule of thumb that the box size should be 10–20 times larger than the beam size (Riggi et al. Reference Riggi2016). The
$4(\texttt{BMAJ}+\texttt{BMIN})/2$
factor represents the bane default box size, where we assume a square box, for simplicity. The limits 3 and 6 are consistent with the rule of thumb that the box size should be 10–20 times larger than the beam size (Riggi et al. Reference Riggi2016). The
![]() $1/4$
and
$1/4$
and
![]() $1/2$
bounds are used for providing a smoothly sliding box (Mohan & Rafferty Reference Mohan and Rafferty2015).
$1/2$
bounds are used for providing a smoothly sliding box (Mohan & Rafferty Reference Mohan and Rafferty2015).
The Typhon optimisation algorithm can be summarised as follows.
• If the RMS box
 $\mu$
-optimisation is desired:
$\mu$
-optimisation is desired:
– Minimise
 $\mu$
over a
$\mu$
over a
 $6\times3$
box_size by step_size search grid, constrained by Equation (3)
$6\times3$
box_size by step_size search grid, constrained by Equation (3)
• Select a centralised
 $n\times n$
image sample-cutout:
$n\times n$
image sample-cutout:
– Use an
 $n^2$
-area rectangle, if non-square image
$n^2$
-area rectangle, if non-square image– Use the full area, if image is too small
• Determine the RMS parameter bounds (Equation (2))
• For each SF:
– If applicable, set the RMS box parameters to the optimised values
– Extract the island parameter bounds from Configuration Management (re. Table 3)
– Optimise the PRD of the sample-cutout:
* Iterate the RMS parameter backwards from RMS
 $_{\max}$
$_{\max}$
* At each RMS step, iterate the island parameter, such that,
 $\sigma_{island}<\sigma_{RMS}$
, otherwise set
$\sigma_{island}<\sigma_{RMS}$
, otherwise set
 $\sigma_{island}=0.999\,\sigma_{RMS}$
$\sigma_{island}=0.999\,\sigma_{RMS}$
* For each RMS-island parameter pair compute the PRD
* Terminate iterations just before the PRD passes below 90%
-
If the PRD is always below 90% choose the highest value.
• Run the SFs on the full image using their optimised parameters
• Archive the results in a tarball
For our initial studies, we have chosen to set
![]() $n=2.5^\circ$
to provide a sufficiently large region of sky to ensure the finder parameters are not biased by small-scale structure in a given image. Also Aegean, PyBDSF, and Selavy are configured to use the RMS box optimisation inputs from bane, with Selavy only accepting the RMS box size. Appendix B provides details of the SFs and their settings used herein.
$n=2.5^\circ$
to provide a sufficiently large region of sky to ensure the finder parameters are not biased by small-scale structure in a given image. Also Aegean, PyBDSF, and Selavy are configured to use the RMS box optimisation inputs from bane, with Selavy only accepting the RMS box size. Appendix B provides details of the SFs and their settings used herein.
For the purposes of placing the SFs on equal footing, we have chosen to restrict Aegean, Caesar and Selavy to single threaded mode, so as to keep the background/noise statistics consistent, at the cost of computational speed. In addition, we keep all of the internal parameters of all of the SFs fixed, instead of tweaking them by hand for each use case. Every effort has been made to keep each SF module as generic as possible.
3.1.4. Hydra
Hydra is the main tool that glues everything together, by running Typhon for
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
images, and producing data products such as diagnostics plots and catalogues. One of main underlying features of Hydra is that it uses a clustering algorithm (Boyce Reference Boyce2018) to relate information between SF components in both
$\mathcal{S}$
images, and producing data products such as diagnostics plots and catalogues. One of main underlying features of Hydra is that it uses a clustering algorithm (Boyce Reference Boyce2018) to relate information between SF components in both
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
images. In addition, Hydra will also accept simulated catalogue input, under a source-finder pseudonym.
$\mathcal{S}$
images. In addition, Hydra will also accept simulated catalogue input, under a source-finder pseudonym.
Fig. 5 shows an example of how the clustering algorithm works. All components between all
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
SF detections (i.e., catalogue rows) are spatially grouped together, with their overlaps forming clumps with unique clump_ids. The clumps are also decomposed into the closest
$\mathcal{S}$
SF detections (i.e., catalogue rows) are spatially grouped together, with their overlaps forming clumps with unique clump_ids. The clumps are also decomposed into the closest
![]() $\mathcal{DS}$
matches, and assigned unique match_ids. The matches are further broken down by SF into subclumps (not shown), and assigned unique subclump_ids. All of this information is compiled into a cluster catalogue (or table), containing the following key reference elements (columns): cluster catalogue ID, clump ID, match ID, subclump ID, SF
$\mathcal{DS}$
matches, and assigned unique match_ids. The matches are further broken down by SF into subclumps (not shown), and assigned unique subclump_ids. All of this information is compiled into a cluster catalogue (or table), containing the following key reference elements (columns): cluster catalogue ID, clump ID, match ID, subclump ID, SF
![]() $\mathcal{D/S}$
catalogue cross-reference ID, and image depth (
$\mathcal{D/S}$
catalogue cross-reference ID, and image depth (
![]() $=\mathcal{D},\,\mathcal{S}$
). In addition, the catalogue contains common SF output parameters, such as RA, Dec, flux density, etc. There is also a clump catalogue, consisting of rows by unique clump_id, of cluster centroid positions, cutout sizes, total number of components, number of components per SF, SFs with the best residual statistics, etc.
$=\mathcal{D},\,\mathcal{S}$
). In addition, the catalogue contains common SF output parameters, such as RA, Dec, flux density, etc. There is also a clump catalogue, consisting of rows by unique clump_id, of cluster centroid positions, cutout sizes, total number of components, number of components per SF, SFs with the best residual statistics, etc.

Figure 6. Derivation of the distance metric used for clustering. Here we assume that the space is locally flat, so that
![]() $\Delta(C_i,C_j)\approx(\delta^2_{\texttt{RA}_{ij}}+\delta^2_{\texttt{Dec}_{ij}})^{1/2}$
, where
$\Delta(C_i,C_j)\approx(\delta^2_{\texttt{RA}_{ij}}+\delta^2_{\texttt{Dec}_{ij}})^{1/2}$
, where
![]() $\delta_{\texttt{RA}_{ij}}=(\texttt{RA}_j-\texttt{RA}_i)\cos(\texttt{Dec}_i)$
and
$\delta_{\texttt{RA}_{ij}}=(\texttt{RA}_j-\texttt{RA}_i)\cos(\texttt{Dec}_i)$
and
![]() $\delta_{\texttt{Dec}_{ij}}=\texttt{Dec}_j-\texttt{Dec}_i$
. The distances from the centres of components
$\delta_{\texttt{Dec}_{ij}}=\texttt{Dec}_j-\texttt{Dec}_i$
. The distances from the centres of components
![]() $C_i$
and
$C_i$
and
![]() $C_j$
to their edges, along a ray between them, is given by
$C_j$
to their edges, along a ray between them, is given by
![]() $r_i$
and
$r_i$
and
![]() $r_j$
, respectively: that is,
$r_j$
, respectively: that is,
![]() $r_\mu$
, is a standard geometrical expression in terms of angle
$r_\mu$
, is a standard geometrical expression in terms of angle
![]() $\beta_\mu=\pi/2-(\theta_\mu-\eta)$
with respect to the ray and the semi-major axis
$\beta_\mu=\pi/2-(\theta_\mu-\eta)$
with respect to the ray and the semi-major axis
![]() $a_\mu$
, where
$a_\mu$
, where
![]() $\theta_\mu$
is the position angle,
$\theta_\mu$
is the position angle,
![]() $\eta=-\tan^{-1}(\delta_{\texttt{Dec}_{ij}}/\delta_{\texttt{RA}_{ij}})$
, and
$\eta=-\tan^{-1}(\delta_{\texttt{Dec}_{ij}}/\delta_{\texttt{RA}_{ij}})$
, and
![]() $\mu=i,\,j$
. The grey area outside the ellipses is the skirt, whose extent is determined by f.
$\mu=i,\,j$
. The grey area outside the ellipses is the skirt, whose extent is determined by f.

Figure 7. Hydra Viewer Infographic: The cutout viewing section of Hydra’s local web-viewer interface. At the top is the navigation bar, which allows the user to navigate by clump ID, go to a specific clump, turn on/off cutout annotations, or examine S/N bins of diagnostic plots such as
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{R}$
, by using the Mode button. The main panel contains
$\mathcal{R}$
, by using the Mode button. The main panel contains
![]() $\mathcal{D}$
(top) and
$\mathcal{D}$
(top) and
![]() $\mathcal{S}$
(bottom) square image cutouts (first column) and SF residual image cutouts (remaining columns), centred about a given clump’s centroid. Here the annotation is turned on, with the neighbouring clumps greyed out. The table at the bottom (not to scale) is the cluster table rows for the clump, with the following columns: cluster catalogue ID, SF catalogue cross-reference ID, clump ID, subclump ID, match ID, SF or
$\mathcal{S}$
(bottom) square image cutouts (first column) and SF residual image cutouts (remaining columns), centred about a given clump’s centroid. Here the annotation is turned on, with the neighbouring clumps greyed out. The table at the bottom (not to scale) is the cluster table rows for the clump, with the following columns: cluster catalogue ID, SF catalogue cross-reference ID, clump ID, subclump ID, match ID, SF or
![]() $\mathcal{J}$
catalogue name, image depth, RA (
$\mathcal{J}$
catalogue name, image depth, RA (
![]() $^\circ$
), Dec (
$^\circ$
), Dec (
![]() $^\circ$
), semi-major axis (
$^\circ$
), semi-major axis (
![]() $^{\prime\prime}$
), semi-minor axis (
$^{\prime\prime}$
), semi-minor axis (
![]() $^{\prime\prime}$
), position angle (
$^{\prime\prime}$
), position angle (
![]() $^\circ$
), total flux density (mJy), bane RMS noise (mJy), S/N (total flux over bane RMS noise), peak flux (mJy beam
$^\circ$
), total flux density (mJy), bane RMS noise (mJy), S/N (total flux over bane RMS noise), peak flux (mJy beam
![]() $^{-1}$
), normalised-residual RMS (mJy (arcmin
$^{-1}$
), normalised-residual RMS (mJy (arcmin
![]() $^2$
beam)
$^2$
beam)
![]() $^{-1}$
), normalised-residual MADFM (mJy (arcmin
$^{-1}$
), normalised-residual MADFM (mJy (arcmin
![]() $^2$
beam)
$^2$
beam)
![]() $^{-1}$
), and normalised-residual
$^{-1}$
), and normalised-residual
![]() $\Sigma I^2$
((mJy (arcmin
$\Sigma I^2$
((mJy (arcmin
![]() $^2$
beam))
$^2$
beam))
![]() $^{-2}$
). The normalised-residual statistics are normalised by the cutout area (arcmin
$^{-2}$
). The normalised-residual statistics are normalised by the cutout area (arcmin
![]() $^2$
). This statistical information is also shown below each cutout, along with the number of components (N), and cutout size (Size, in arcmin). This figure is to illustrate the layout of the Hydra viewer, not the details. It shows screen shots from the Hydra Viewer pasted together, hence the fonts appear small. The data at the bottom is raw output from the cluster table, which is not rounded in this version of the software.
$^2$
). This statistical information is also shown below each cutout, along with the number of components (N), and cutout size (Size, in arcmin). This figure is to illustrate the layout of the Hydra viewer, not the details. It shows screen shots from the Hydra Viewer pasted together, hence the fonts appear small. The data at the bottom is raw output from the cluster table, which is not rounded in this version of the software.
Fig. 6 shows the derivation of the distance metric used in the clustering algorithm. The algorithm uses the following distance metric constraint to determine the overlap between two elliptical components,
![]() $C_i$
and
$C_i$
and
![]() $C_j$
, with centre-to-edge distances,
$C_j$
, with centre-to-edge distances,
![]() $r_i$
and
$r_i$
and
![]() $r_j$
, along an adjoining ray.
$r_j$
, along an adjoining ray.
where
is the distance metric, and
 \begin{equation*} r_\mu=\frac{a_\mu b_\mu}{\sqrt{a_\mu^2\cos^2(\theta_\mu-\eta)+b_\mu^2\sin^2(\theta_\mu-\eta)}}\,,\nonumber\end{equation*}
\begin{equation*} r_\mu=\frac{a_\mu b_\mu}{\sqrt{a_\mu^2\cos^2(\theta_\mu-\eta)+b_\mu^2\sin^2(\theta_\mu-\eta)}}\,,\nonumber\end{equation*}
are the centre-to-edge distances, for
![]() $\mu=i,j$
, with
$\mu=i,j$
, with
![]() $a_\mu$
is the semi-major axis,
$a_\mu$
is the semi-major axis,
![]() $b_\mu$
is the semi-minor axis, and
$b_\mu$
is the semi-minor axis, and
![]() $\theta_\mu$
is the position angle (defined in the same manner as the beam PA, Greisen Reference Greisen2017). So components satisfying this constraint are clumped together.
$\theta_\mu$
is the position angle (defined in the same manner as the beam PA, Greisen Reference Greisen2017). So components satisfying this constraint are clumped together.
Hydra also provides a web-viewer (known as the Hydra Viewer) for exploring image and residual image cutouts by clump_id, along with corresponding cluster table information. Fig. 7 provides a detailed description of the Hydra Viewer’s cutout interface. As indicated in the figure, the viewer has radio component annotations that can be toggled on/off. Fig. 8 provides a more detailed example. Table 4 describes the annotation colours, which are stored as metadata in Hydra’s Configuration Management (Fig. 3).
The following is a list of the data products produced by Hydra:
• Typhon Metrics
–
 $\mathcal{D/S}$
Diagnostic Plots of
$\mathcal{D/S}$
Diagnostic Plots of
* PRD
* PRD CPU Times
* Residual RMS
* Residual MADFM
* Residual
 $\Sigma I^2$
$\Sigma I^2$
– Table of
 $\mathcal{D}$
and
$\mathcal{D}$
and
 $\mathcal{S}$
optimised RMS and island parameters
$\mathcal{S}$
optimised RMS and island parameters
•
 $\mathcal{D/S}$
Catalogues
$\mathcal{D/S}$
Catalogues
– SF Catalogues
– Cluster Catalogue
– Clump Catalogue
• Optional Simulated Input Catalogue
•
 $\mathcal{D/S}$
Cutouts
$\mathcal{D/S}$
Cutouts
– Un/annotated Images
– Un/annotated Residual Images
•
 $\mathcal{D/S}$
Diagnostic Plots
$\mathcal{D/S}$
Diagnostic Plots
– Clump Size Distributions
– Detections vs S/N
–
 $\mathcal{C}$
vs S/N
$\mathcal{C}$
vs S/N–
 $\mathcal{R}$
vs S/N
$\mathcal{R}$
vs S/N– Flux-Ratios:
 $S_{out}/S_{in}$
vs S/N
$S_{out}/S_{in}$
vs S/N– False-Positives vs S/N
• Hydra Viewer: Local Web-browser Tool
All of this information is stored in a tarball. The Hydra Viewer allows the user to view all of these data products. The cutout viewer portion is linked only to the cluster catalogue. It is accessible through an index.html file in the main tar directory.
4. Completeness and reliability metrics
Completeness and reliability metrics can be generated through various combinations of deep, shallow, and injected sources. Fig. 9 shows a Venn diagram of the overlapping possibilities. In addition, we need to be careful in our definitions of these metrics.
Here we use a clustering approach to spatially match our detections (Equation (4)). An alternative method is to use a cutoff distance in a catalogue cross-match (e.g., Huynh et al. Reference Huynh, Hopkins, Norris, Hancock, Murphy, Jurek and Whitting2012; Hopkins et al. Reference Hopkins2015; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019).Footnote m Depending on the cutoff distance adopted, ‘locally,’ this approach may lead to associations between adjacent clumps that may not actually be related. The clustering approach aims to mitigate against this effect.
Table 4. SF annotation colours.


Figure 8. An example of a
![]() $\mathcal{D}$
-image cutout, with annotations turned on, consisting of 4 Aegean, 2 ProFound, 2 PyBDSF, and 2 Selavy overlapping
$\mathcal{D}$
-image cutout, with annotations turned on, consisting of 4 Aegean, 2 ProFound, 2 PyBDSF, and 2 Selavy overlapping
![]() $\mathcal{D}$
-image catalogue components. The label at the top indicates it corresponds to clump_id 243, and the numbers at the centres of the cyan boxes are the match_ids (369 through 372).
$\mathcal{D}$
-image catalogue components. The label at the top indicates it corresponds to clump_id 243, and the numbers at the centres of the cyan boxes are the match_ids (369 through 372).
Completeness (
![]() $\mathcal{C}$
) is the fraction of real detections to real sources, and reliability (
$\mathcal{C}$
) is the fraction of real detections to real sources, and reliability (
![]() $\mathcal{R}$
) is the fraction of real detections to detected sources (Fig. 9). Here we define these metrics in terms of ‘real’ injected (simulated) sources (
$\mathcal{R}$
) is the fraction of real detections to detected sources (Fig. 9). Here we define these metrics in terms of ‘real’ injected (simulated) sources (
![]() $\mathcal{J}$
) vs deep (
$\mathcal{J}$
) vs deep (
![]() $\mathcal{D}$
) and shallow (
$\mathcal{D}$
) and shallow (
![]() $\mathcal{S}$
) detections and, ‘assumed-real’ deep detections vs shallow detections. In the case where the sources are known (i.e., injected), we take the fraction of real–deep (
$\mathcal{S}$
) detections and, ‘assumed-real’ deep detections vs shallow detections. In the case where the sources are known (i.e., injected), we take the fraction of real–deep (
![]() $\mathcal{D}\cap\mathcal{J}$
) or real–shallow (
$\mathcal{D}\cap\mathcal{J}$
) or real–shallow (
![]() $\mathcal{S}\cap\mathcal{J}$
) detections to the injected sources for our completeness,
$\mathcal{S}\cap\mathcal{J}$
) detections to the injected sources for our completeness,
or
respectively.Footnote n Similarly, the fraction of real–deep or real–shallow detections to the corresponding deep or shallow detections give the reliability
or
respectively. In the case where no true underlying sources are known we use the deep detections as a proxy, and take the fraction of real–shallow detections to deep detections for our completeness,
and the fraction of real–shallow to shallow detections for our reliability,

Figure 9. Venn diagram of completeness and reliability, for sets of deep (
![]() $\mathcal{D}$
), shallow (
$\mathcal{D}$
), shallow (
![]() $\mathcal{S}$
), and injected (
$\mathcal{S}$
), and injected (
![]() $\mathcal{J}$
) sources.
$\mathcal{J}$
) sources.
We can take this one step further by asking the question, ‘Given our knowledge of injected sources, how good are our measures of deep–shallow completeness (
![]() $\mathcal{C_{\mathcal{DS}}}$
) and reliability (
$\mathcal{C_{\mathcal{DS}}}$
) and reliability (
![]() $\mathcal{R_{\mathcal{DS}}}$
)?’ From this, we define the fraction of real–deep–shallow detections,
$\mathcal{R_{\mathcal{DS}}}$
)?’ From this, we define the fraction of real–deep–shallow detections,
![]() $(\mathcal{D}\cap\mathcal{J})\cap(\mathcal{S}\cap\mathcal{J})$
, to real–deep detections,
$(\mathcal{D}\cap\mathcal{J})\cap(\mathcal{S}\cap\mathcal{J})$
, to real–deep detections,
![]() $\mathcal{D}\cap\mathcal{J}$
, as our goodness of completeness,
$\mathcal{D}\cap\mathcal{J}$
, as our goodness of completeness,
and the fraction of real–deep–shallow detections to real-shallow detections,
![]() $\mathcal{S}\cap\mathcal{J}$
, as our goodness of reliability,
$\mathcal{S}\cap\mathcal{J}$
, as our goodness of reliability,
Table 5 summarises all of our completeness and reliability metrics (Equations (5) through (12)).Footnote o
Table 5. Completeness/reliability metrics (see Fig. 9) in terms of deep (
![]() $\mathcal{D}$
), shallow (
$\mathcal{D}$
), shallow (
![]() $\mathcal{S}$
), and injected (
$\mathcal{S}$
), and injected (
![]() $\mathcal{J}$
) sources.
$\mathcal{J}$
) sources.

Fig. 10 shows examples of deep–shallow source component overlaps,
![]() $\mathcal{S}\cap\mathcal{D}$
, to illustrate the calculation of
$\mathcal{S}\cap\mathcal{D}$
, to illustrate the calculation of
![]() $\mathcal{C_{\mathcal{DS}}}$
and
$\mathcal{C_{\mathcal{DS}}}$
and
![]() $\mathcal{R_{\mathcal{DS}}}$
. Matches are done pair-wise, within clumps, between the closest centres of overlapping deep–shallow components. This method is more precise than a typical fixed separation nearest neighbour approach (Hopkins et al. Reference Hopkins2015; Riggi et al. Reference Riggi2019), as it ensures source components always overlap. The
$\mathcal{R_{\mathcal{DS}}}$
. Matches are done pair-wise, within clumps, between the closest centres of overlapping deep–shallow components. This method is more precise than a typical fixed separation nearest neighbour approach (Hopkins et al. Reference Hopkins2015; Riggi et al. Reference Riggi2019), as it ensures source components always overlap. The
![]() $|\mathcal{S}\cap\mathcal{D}|:|\mathcal{D}|$
and
$|\mathcal{S}\cap\mathcal{D}|:|\mathcal{D}|$
and
![]() $|\mathcal{S}\cap\mathcal{D}|:|\mathcal{S}|$
ratios are then binned with respect to the
$|\mathcal{S}\cap\mathcal{D}|:|\mathcal{S}|$
ratios are then binned with respect to the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
flux densities (or S/N), respectively, producing
$\mathcal{S}$
flux densities (or S/N), respectively, producing
![]() $\mathcal{C_{\mathcal{DS}}}$
vs
$\mathcal{C_{\mathcal{DS}}}$
vs
![]() $\mathcal{D}$
completeness and
$\mathcal{D}$
completeness and
![]() $\mathcal{R_{\mathcal{DS}}}$
vs
$\mathcal{R_{\mathcal{DS}}}$
vs
![]() $\mathcal{S}$
reliability histograms.
$\mathcal{S}$
reliability histograms.

Figure 10. Examples of deep (blue) and shallow (amber) source component overlaps,
![]() $\mathcal{C_{\mathcal{DS}}}=(\mathcal{S}\cap\mathcal{D})/\mathcal{D}$
and
$\mathcal{C_{\mathcal{DS}}}=(\mathcal{S}\cap\mathcal{D})/\mathcal{D}$
and
![]() $\mathcal{R_{\mathcal{DS}}}=(\mathcal{S}\cap\mathcal{D})/\mathcal{S}$
. Real-shallow detections are indicated by overlapping pair-wise deep-shallow detections (
$\mathcal{R_{\mathcal{DS}}}=(\mathcal{S}\cap\mathcal{D})/\mathcal{S}$
. Real-shallow detections are indicated by overlapping pair-wise deep-shallow detections (
![]() $\mathcal{S}\cap\mathcal{D}$
), whose centres are closest. The dash-lines indicate clumps of component extent overlays.
$\mathcal{S}\cap\mathcal{D}$
), whose centres are closest. The dash-lines indicate clumps of component extent overlays.
5. Validation
In this section we use
![]() $2^\circ\times2^\circ$
simulated-compact (CMP) and simulated-extended (EXT) image data to characterise the performance of Hydra, and validate some new metrics. In particular, the simulated data are used to explore and develop metrics that can be used for real images where the ground truth is unknown. A preliminary discussion on SF performance is also presented. Paper II is focused on cross-SF comparison, using our simulated data along with some real data.
$2^\circ\times2^\circ$
simulated-compact (CMP) and simulated-extended (EXT) image data to characterise the performance of Hydra, and validate some new metrics. In particular, the simulated data are used to explore and develop metrics that can be used for real images where the ground truth is unknown. A preliminary discussion on SF performance is also presented. Paper II is focused on cross-SF comparison, using our simulated data along with some real data.
5.1. Image data
5.1.1. Simulated compact sources, CMP
The simulated image, shown in Fig. 11, is produced in two steps; generation of a noise image, followed by the addition of artificial sources. We use miriad (Sault, Teuben, & Wright Reference Sault, Teuben, Wright, Shaw, Payne and Hayes1995) to generate the artificial noise image, using the following steps. The imgen task was used to produce a 1800
![]() $\times$
1800 pixel image, with 4” pixels, (i.e., a
$\times$
1800 pixel image, with 4” pixels, (i.e., a
![]() $2^{\circ} \times 2^{\circ}$
field) populated by random Gaussian noise of RMS
$2^{\circ} \times 2^{\circ}$
field) populated by random Gaussian noise of RMS
![]() $20\,\unicode{x03BC}$
Jy beam
$20\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
. This image was convolved using convol to mimic a 15” FWHM beam, which has the effect of increasing the noise level by a factor of 2.8, so the resulting image is then scaled using maths to divide by this factor, restoring the original noise level of
$^{-1}$
. This image was convolved using convol to mimic a 15” FWHM beam, which has the effect of increasing the noise level by a factor of 2.8, so the resulting image is then scaled using maths to divide by this factor, restoring the original noise level of
![]() $20\,\unicode{x03BC}$
Jy beam
$20\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
.
$^{-1}$
.

Figure 11. Simulated map with point-like (compact) sources. The coordinates are arbitrarily set, and the FWHM is set to 15”.
To generate the properties of the artificial sources, we use the 6th order polynomial fit to the 1.4 GHz source counts from Hopkins et al. (Reference Hopkins, Afonso, Chan, Cram, Georgakakis and Mobasher2003), which is consistent with more recent source count determinations for the flux density range considered here (e.g., Gürkan et al. Reference Gürkan2022, and references therein). A sequence of 34 exponentially spaced bins in flux density was defined, ranging from
![]() $50\,\unicode{x03BC}$
Jy to
$50\,\unicode{x03BC}$
Jy to
![]() $1\,$
Jy, and within each bin the number of sources was calculated from the source count model. The flux density for each artificial source was assigned randomly between the extrema of the bin in which it lies. Source positions were also assigned randomly, with no attempt to mimic the clustering properties of real sources. For the
$1\,$
Jy, and within each bin the number of sources was calculated from the source count model. The flux density for each artificial source was assigned randomly between the extrema of the bin in which it lies. Source positions were also assigned randomly, with no attempt to mimic the clustering properties of real sources. For the
![]() $2^{\circ} \times 2^{\circ}$
field with a flux density limit of
$2^{\circ} \times 2^{\circ}$
field with a flux density limit of
![]() $50\,\unicode{x03BC}$
Jy, we end up with a list of 9075 artificial sources.
$50\,\unicode{x03BC}$
Jy, we end up with a list of 9075 artificial sources.
These sources were added to the noise image using the Python module Astropy (Astropy Collaboration et al. Reference Astropy Collaboration2013, Reference Astropy Collaboration2018) by constructing 2D Gaussian models with the FWHM of the restoring beam (15”) and scaling the amplitude to represent the randomly assigned peak flux density of the source. Given the sources modelled here are assumed to be point-like (compact), the peak flux density for a source has the same amplitude as the integrated flux density. Using this Gaussian model for each source, we generated an image array for each source to be added into the simulated image. We used Astropy again to convert the RA/Dec location of the source to pixel locations and each source was added to the simulated image at the desired location.
5.1.2. Simulated extended sources, EXT
Following a similar procedure as in Section 5.1.1, we generated a sky model of size 1800
![]() $\times$
1800 pixels (
$\times$
1800 pixels (
![]() $4^{\prime\prime}$
pixel size, 2
$4^{\prime\prime}$
pixel size, 2
![]() $^{\circ}\times$
2
$^{\circ}\times$
2
![]() $^{\circ}$
field of view) with both point-like and extended sources injected. The noise level is again set to 20
$^{\circ}$
field of view) with both point-like and extended sources injected. The noise level is again set to 20
![]() $\unicode{x03BC}$
Jy beam
$\unicode{x03BC}$
Jy beam
![]() $^{-1}$
. Extended sources are 2D elliptical Gaussians with randomised position angle and axis ratio, with axis ratio varying between 0.4 to 1. A maximum major axis size was set at three times the synthesised beam size (
$^{-1}$
. Extended sources are 2D elliptical Gaussians with randomised position angle and axis ratio, with axis ratio varying between 0.4 to 1. A maximum major axis size was set at three times the synthesised beam size (
![]() $45^{\prime\prime}$
, with a
$45^{\prime\prime}$
, with a
![]() $15^{\prime\prime}$
FWHM beam, as in Section 5.1.1).
$15^{\prime\prime}$
FWHM beam, as in Section 5.1.1).
A total of 9974 artificial sources were injected, corresponding to a source density of 2500 deg
![]() $^{-2}$
, with 10% being extended sources. The peak flux densities S of both point-like and extended sources were set to follow an exponential distribution
$^{-2}$
, with 10% being extended sources. The peak flux densities S of both point-like and extended sources were set to follow an exponential distribution
![]() $10^{-\lambda S}$
with
$10^{-\lambda S}$
with
![]() $\lambda$
=1.6, consistent with that seen in early ASKAP observations of the Stellar Continuum Originating from Radio Physics In Our Galaxy (Scorpio, Umana et al. Reference Umana2015) field (Riggi et al. Reference Riggi2021). The minimum peak flux density for all sources was set at
$\lambda$
=1.6, consistent with that seen in early ASKAP observations of the Stellar Continuum Originating from Radio Physics In Our Galaxy (Scorpio, Umana et al. Reference Umana2015) field (Riggi et al. Reference Riggi2021). The minimum peak flux density for all sources was set at
![]() $50\,\unicode{x03BC}$
Jy and the maximum fixed at 1 Jy for compact sources and 1 mJy for extended sources. The final simulated image, shown in Fig. 12, was produced by convolving this input sky model using the CASAFootnote p imsmooth task and a target resolution of
$50\,\unicode{x03BC}$
Jy and the maximum fixed at 1 Jy for compact sources and 1 mJy for extended sources. The final simulated image, shown in Fig. 12, was produced by convolving this input sky model using the CASAFootnote p imsmooth task and a target resolution of
![]() $15^{\prime\prime}$
.
$15^{\prime\prime}$
.

Figure 12. Simulated image with both point-like (compact) and extended sources. The sky coordinates are arbitrarily chosen.
It is important to note here that, unlike the compact source simulation above where the faintest injected source lies at
![]() $\mbox{(S/N)}_{\min}\sim2.5$
, in the extended source simulated image 20.6% of the injected sources fall below
$\mbox{(S/N)}_{\min}\sim2.5$
, in the extended source simulated image 20.6% of the injected sources fall below
![]() $\mbox{S/N}=1$
. This is by design, to provide a more realistic image, and to test the impact on the SFs of having real sources lying below the noise level (re. M. M. Boyce et al., in preparation).
$\mbox{S/N}=1$
. This is by design, to provide a more realistic image, and to test the impact on the SFs of having real sources lying below the noise level (re. M. M. Boyce et al., in preparation).
Table 6. Hydra
![]() $\mu$
-optimised box_size and step_size inputs for Aegean, PyBDSF, and Selavy,
$\mu$
-optimised box_size and step_size inputs for Aegean, PyBDSF, and Selavy,
![]() $^{\rm a}$
using CMP and EXT
$^{\rm a}$
using CMP and EXT
![]() $\mathcal{D/S}$
-image data.
$\mathcal{D/S}$
-image data.

![]() $\!\!^{\rm a}$
Selavy only accepts box_size.
$\!\!^{\rm a}$
Selavy only accepts box_size.
5.2. Typhon statistics
5.2.1. Optimisation run results
Hydra uses Typhon to set the RMS box and island parameters for each SF (Aegean, Caesar, ProFound, PyBDSF, and Selavy) to ensure a 90% PRD cutoff. The RMS box parameters, obtained from Typhon’s
![]() $\mu$
-optimisation routine, were used by Aegean, PyBDSF, and Selavy. An
$\mu$
-optimisation routine, were used by Aegean, PyBDSF, and Selavy. An
![]() $\mathcal{S}$
-image was generated by Homados, and RMS box and island parameters similarly estimated. Tables 6 and 7 summarise these results for our CMP and EXT images.
$\mathcal{S}$
-image was generated by Homados, and RMS box and island parameters similarly estimated. Tables 6 and 7 summarise these results for our CMP and EXT images.
For the CMP source
![]() $\mathcal{D}$
-image,
$\mathcal{D}$
-image,
![]() $\mu\sim22\,\unicode{x03BC}$
Jy beam
$\mu\sim22\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
(Table 6) which is consistent with the design RMS noise of
$^{-1}$
(Table 6) which is consistent with the design RMS noise of
![]() $20\,\unicode{x03BC}$
Jy beam
$20\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
(re. Section 5.1). For the EXT source
$^{-1}$
(re. Section 5.1). For the EXT source
![]() $\mathcal{D}$
-image,
$\mathcal{D}$
-image,
![]() $\mu\sim68\,\unicode{x03BC}$
Jy beam
$\mu\sim68\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
which is higher due to the inclusion of extended structures with a slightly higher source density, and the fact that the box size has doubled. This is consistent with an average source size increase from
$^{-1}$
which is higher due to the inclusion of extended structures with a slightly higher source density, and the fact that the box size has doubled. This is consistent with an average source size increase from
![]() $15^{\prime\prime}$
to
$15^{\prime\prime}$
to
![]() $30^{\prime\prime}$
. We also note that
$30^{\prime\prime}$
. We also note that
![]() $\mu_{\mathcal{S}}/\mu_{\mathcal{D}}\sim 5$
for all images, which is consistent with the factor of 5 noise increase for the
$\mu_{\mathcal{S}}/\mu_{\mathcal{D}}\sim 5$
for all images, which is consistent with the factor of 5 noise increase for the
![]() $\mathcal{S}$
-images (Section 3.1.1). So the RMS box statistics are consistent with what might be expected from the simulated images.
$\mathcal{S}$
-images (Section 3.1.1). So the RMS box statistics are consistent with what might be expected from the simulated images.
In Table 7 we notice, in the broadest sense, that the RMS and island parameters are similar for the
![]() $\mathcal{D/S}$
-images, row-wise. Fig. 13 shows stacked plots of
$\mathcal{D/S}$
-images, row-wise. Fig. 13 shows stacked plots of
![]() $\mathcal{D/S}$
source counts for the images. In the CMP and EXT
$\mathcal{D/S}$
source counts for the images. In the CMP and EXT
![]() $\mathcal{D}$
-images, there is some variability in the source counts, that is,
$\mathcal{D}$
-images, there is some variability in the source counts, that is,
![]() $N\sim4\,650\pm890$
, except for Selavy being consistently lower by
$N\sim4\,650\pm890$
, except for Selavy being consistently lower by
![]() $N\sim1\,770\pm950$
. In the
$N\sim1\,770\pm950$
. In the
![]() $\mathcal{S}$
-image case, the variability is fairly tight, with
$\mathcal{S}$
-image case, the variability is fairly tight, with
![]() $N_{\small {\rm CMP}}\sim661\pm54$
and
$N_{\small {\rm CMP}}\sim661\pm54$
and
![]() $N_{\small {\rm EXT}}\sim1\,258\pm70$
, except for Selavy which is consistently low with
$N_{\small {\rm EXT}}\sim1\,258\pm70$
, except for Selavy which is consistently low with
![]() $N_{\small {\rm CMP}}=427$
and
$N_{\small {\rm CMP}}=427$
and
![]() $N_{\small {\rm EXT}}=787$
.
$N_{\small {\rm EXT}}=787$
.
Table 7. Typhon run statistics for CMP and EXT images, with SF, image depth, SF RMS parameter (
![]() $n_{rms}$
[
$n_{rms}$
[
![]() $\sigma$
]), SF island parameter (
$\sigma$
]), SF island parameter (
![]() $n_{island}$
[
$n_{island}$
[
![]() $\sigma$
]), source counts (N), residual RMS (
$\sigma$
]), source counts (N), residual RMS (
![]() $\unicode{x03BC}$
Jy beam
$\unicode{x03BC}$
Jy beam
![]() $^{-1}$
), and residual MADFM (
$^{-1}$
), and residual MADFM (
![]() $\unicode{x03BC}$
Jy beam
$\unicode{x03BC}$
Jy beam
![]() $^{-1}$
) columns.
$^{-1}$
) columns.
![]() $^{\rm a}$
$^{\rm a}$

![]() $\!\!^{\rm a}$
The MADFM estimators are normalised by 0.6744888 (Whiting Reference Whiting2012).
$\!\!^{\rm a}$
The MADFM estimators are normalised by 0.6744888 (Whiting Reference Whiting2012).

Figure 13. SF CMP and EXT
![]() $\mathcal{D/S}$
-image detection stacked plots (re. the N columns of Table 7).
$\mathcal{D/S}$
-image detection stacked plots (re. the N columns of Table 7).
For the CMP
![]() $\mathcal{D}$
-image, the RMS and MADFM residual statistics are all
$\mathcal{D}$
-image, the RMS and MADFM residual statistics are all
![]() $\sim$
$\sim$
![]() $19\,\unicode{x03BC}$
Jy beam
$19\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
, with the exception of Selavy having a significantly higher RMS (
$^{-1}$
, with the exception of Selavy having a significantly higher RMS (
![]() $\sim$
$\sim$
![]() $45\,\unicode{x03BC}$
Jy beam
$45\,\unicode{x03BC}$
Jy beam
![]() $^{-1}$
), likely the primary cause for the reduction in numbers of detected sources it reports. For the EXT
$^{-1}$
), likely the primary cause for the reduction in numbers of detected sources it reports. For the EXT
![]() $\mathcal{D}$
-image, the RMS values increase in order from ProFound, Caesar, Aegean, PyBDSF, to Selavy, with the latter three being comparable to the former being at extreme end. This is also reflected in their MAFDMs, although here the values are somewhat comparable. For the
$\mathcal{D}$
-image, the RMS values increase in order from ProFound, Caesar, Aegean, PyBDSF, to Selavy, with the latter three being comparable to the former being at extreme end. This is also reflected in their MAFDMs, although here the values are somewhat comparable. For the
![]() $\mathcal{S}$
-image case, everything is similar within each image data set, except for Selavy having a higher RMS in the EXT image case. These observed discrepancies for Selavy are likely due to its use of robust statistics in the background estimation (Section B.5). In contrast, the MADFM is similar in both cases for all SFs.
$\mathcal{S}$
-image case, everything is similar within each image data set, except for Selavy having a higher RMS in the EXT image case. These observed discrepancies for Selavy are likely due to its use of robust statistics in the background estimation (Section B.5). In contrast, the MADFM is similar in both cases for all SFs.
Table 8 shows ratios of deep-to-injected (
![]() $\mathcal{D}\,:\,\mathcal{J}$
) and shallow-to-deep (
$\mathcal{D}\,:\,\mathcal{J}$
) and shallow-to-deep (
![]() $\mathcal{S}\,:\,\mathcal{D}$
) source counts: that is,
$\mathcal{S}\,:\,\mathcal{D}$
) source counts: that is,
![]() $\mathcal{D}\,:\,\mathcal{J}$
indicates the fraction of sources recovered in the simulated images, whereas
$\mathcal{D}\,:\,\mathcal{J}$
indicates the fraction of sources recovered in the simulated images, whereas
![]() $\mathcal{S}\,:\,\mathcal{D}$
indicates the recovery rate assuming the deep detections are ‘real’. Also included are
$\mathcal{S}\,:\,\mathcal{D}$
indicates the recovery rate assuming the deep detections are ‘real’. Also included are
![]() $\mathcal{S}\,:\,\mathcal{J}$
recovery rates, for comparison.Footnote q The
$\mathcal{S}\,:\,\mathcal{J}$
recovery rates, for comparison.Footnote q The
![]() $\mathcal{D}\,:\,\mathcal{J}$
recovery rates are not expected to reach 100%, as the simulations includes low S/N sources, and for EXT sources, some lying below S/N
$\mathcal{D}\,:\,\mathcal{J}$
recovery rates are not expected to reach 100%, as the simulations includes low S/N sources, and for EXT sources, some lying below S/N
![]() $=1$
. The
$=1$
. The
![]() $\mathcal{S}\,:\,\mathcal{D}$
recovery rate is lower for CMP sources than EXT, which both track consistently with
$\mathcal{S}\,:\,\mathcal{D}$
recovery rate is lower for CMP sources than EXT, which both track consistently with
![]() $\mathcal{D}\,:\,\mathcal{J}$
.Footnote r This may be due to some confusion in the EXT image (Fig. 12), given the
$\mathcal{D}\,:\,\mathcal{J}$
.Footnote r This may be due to some confusion in the EXT image (Fig. 12), given the
![]() $\mathcal{S}\,:\,\mathcal{J}$
recovery rates are similar.
$\mathcal{S}\,:\,\mathcal{J}$
recovery rates are similar.
Table 8. Ratios of deep-to-injected (
![]() $\mathcal{D}\,:\,\mathcal{J}$
) shallow-to-injected (
$\mathcal{D}\,:\,\mathcal{J}$
) shallow-to-injected (
![]() $\mathcal{S}\,:\,\mathcal{J}$
), and shallow-to-deep (
$\mathcal{S}\,:\,\mathcal{J}$
), and shallow-to-deep (
![]() $\mathcal{S}\,:\,\mathcal{D}$
) sources. The
$\mathcal{S}\,:\,\mathcal{D}$
) sources. The
![]() $\mathcal{D}/\mathcal{S}$
source counts (N) are provided in Table 7, and the injected source counts are 9075 and 9974 for CMP and EXT sources, respectively (re. Section 5.1).
$\mathcal{D}/\mathcal{S}$
source counts (N) are provided in Table 7, and the injected source counts are 9075 and 9974 for CMP and EXT sources, respectively (re. Section 5.1).

The consistency of the RMS box, MADFM,
![]() $\mathcal{D}\,:\,\mathcal{J}$
,
$\mathcal{D}\,:\,\mathcal{J}$
,
![]() $\mathcal{S}\,:\,\mathcal{J}$
, and
$\mathcal{S}\,:\,\mathcal{J}$
, and
![]() $\mathcal{S}\,:\,\mathcal{D}$
statistics provides a good indication that Hydra’s optimisation routines are performing robustly.
$\mathcal{S}\,:\,\mathcal{D}$
statistics provides a good indication that Hydra’s optimisation routines are performing robustly.
5.2.2. Source size distributions
Fig. 14 shows the major-axis distribution for our simulated image data. Both the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
source detections are combined, as the
$\mathcal{S}$
source detections are combined, as the
![]() $\mathcal{S}$
provides no contrasting information and its statistics are quite low (Fig. 13). Note that the size estimates for different SFs use different methods and are not necessarily directly comparable. Those SFs that fit Gaussians to source components report size as a FWHM, while others (such as ProFound) use different measures, such as a flux-weighted fit (see Appendix B for details).
$\mathcal{S}$
provides no contrasting information and its statistics are quite low (Fig. 13). Note that the size estimates for different SFs use different methods and are not necessarily directly comparable. Those SFs that fit Gaussians to source components report size as a FWHM, while others (such as ProFound) use different measures, such as a flux-weighted fit (see Appendix B for details).

Figure 14. Major-axis distributions for (a) CMP and (b) EXT sources (with
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
both included). The vertical dashed-line represents the beam size. The distributions of the injected sources are shown in grey. Recall that size estimates between SFs are not necessarily directly comparable as they are estimated using different methods.
$\mathcal{S}$
both included). The vertical dashed-line represents the beam size. The distributions of the injected sources are shown in grey. Recall that size estimates between SFs are not necessarily directly comparable as they are estimated using different methods.
For the CMP source case, ProFound and PyBDSF tend to overestimate the source sizes. This is likely due to deblending issues or the incorporation of noise spikes. As for EXT sources, PyBDSF tends to most accurately recover the extended source sizes, but, along with Caesar also has the most outliers. These could be attributed to size overestimates due to inclusion of noise spikes or adjacent sources in the fitted sizes. All other SFs tend to marginally underestimate the EXT source sizes. Components smaller than
![]() $15^{\prime\prime}$
are attributed primarily to noise spikes, but also occasionally to underestimating the source sizes.
$15^{\prime\prime}$
are attributed primarily to noise spikes, but also occasionally to underestimating the source sizes.
5.3. Completeness and reliability
In this section, we discuss deep (
![]() $\mathcal{D}$
) and shallow (
$\mathcal{D}$
) and shallow (
![]() $\mathcal{S}$
) completeness (
$\mathcal{S}$
) completeness (
![]() $\mathcal{C}$
) and reliability (
$\mathcal{C}$
) and reliability (
![]() $\mathcal{R}$
) (see Section 4). We then provide justification for using deep-shallow (
$\mathcal{R}$
) (see Section 4). We then provide justification for using deep-shallow (
![]() $\mathcal{DS}$
) completeness (
$\mathcal{DS}$
) completeness (
![]() $\mathcal{C_{DS}}$
) and reliability (
$\mathcal{C_{DS}}$
) and reliability (
![]() $\mathcal{R_{DS}}$
) metrics for real images, and qualifications on their use, through goodness of completeness (
$\mathcal{R_{DS}}$
) metrics for real images, and qualifications on their use, through goodness of completeness (
![]() $\mathcal{\tilde{C}_{DS}}$
) and goodness of reliability (
$\mathcal{\tilde{C}_{DS}}$
) and goodness of reliability (
![]() $\mathcal{\tilde{R}_{DS}}$
) results.
$\mathcal{\tilde{R}_{DS}}$
) results.
5.3.1. Simulated sources
Fig. 15 shows
![]() $\mathcal{C_{D}}$
vs S/N (top) and
$\mathcal{C_{D}}$
vs S/N (top) and
![]() $\mathcal{R_{D}}$
vs S/N (bottom) for CMP (left) and EXT (right)
$\mathcal{R_{D}}$
vs S/N (bottom) for CMP (left) and EXT (right)
![]() $\mathcal{D}$
-images, where the signal-to-noise (S/N) is the ratio of the
$\mathcal{D}$
-images, where the signal-to-noise (S/N) is the ratio of the
![]() $\mathcal{D}$
-signal to
$\mathcal{D}$
-signal to
![]() $\mathcal{D}$
-noise. Fig. 16 shows the corresponding results for
$\mathcal{D}$
-noise. Fig. 16 shows the corresponding results for
![]() $\mathcal{S}$
-images, where S/N is the ratio of the
$\mathcal{S}$
-images, where S/N is the ratio of the
![]() $\mathcal{S}$
-signal to
$\mathcal{S}$
-signal to
![]() $\mathcal{S}$
-noise.
$\mathcal{S}$
-noise.

Figure 15. Simulated
![]() $\mathcal{D}$
-image compact (left) and extended (right) source
$\mathcal{D}$
-image compact (left) and extended (right) source
![]() $\mathcal{C_{D}}$
(top) and
$\mathcal{C_{D}}$
(top) and
![]() $\mathcal{R_{D}}$
(bottom) vs S/N (
$\mathcal{R_{D}}$
(bottom) vs S/N (
![]() $\mathcal{D}$
-signal/Deep-noise) plots. The
$\mathcal{D}$
-signal/Deep-noise) plots. The
![]() $\mathcal{D}$
-noise is computed using bane.
$\mathcal{D}$
-noise is computed using bane.

Figure 16. Simulated
![]() $\mathcal{S}$
-image compact (left) and extended (right) source
$\mathcal{S}$
-image compact (left) and extended (right) source
![]() $\mathcal{C_{S}}$
(top) and
$\mathcal{C_{S}}$
(top) and
![]() $\mathcal{R_{S}}$
(bottom) vs S/N (
$\mathcal{R_{S}}$
(bottom) vs S/N (
![]() $\mathcal{D}$
-signal/
$\mathcal{D}$
-signal/
![]() $\mathcal{S}$
-noise) plots. The
$\mathcal{S}$
-noise) plots. The
![]() $\mathcal{S}$
-noise is computed using bane.
$\mathcal{S}$
-noise is computed using bane.
For CMP sources all SFs show a similar behaviour in general. The completeness metric starts to decline slowly from 100% at S/N
![]() $\lesssim 30$
, and drops rapidly toward zero below S/N
$\lesssim 30$
, and drops rapidly toward zero below S/N
![]() $\sim 5$
. False detections are typically limited to about 10% of the sample down to S/N
$\sim 5$
. False detections are typically limited to about 10% of the sample down to S/N
![]() $\sim 5$
, but can appear in some SFs as high as S/N
$\sim 5$
, but can appear in some SFs as high as S/N
![]() $\sim 30$
. In general terms, Aegean provides the highest level of completeness at any given S/N, with a well-behaved decline in reliability below S/N
$\sim 30$
. In general terms, Aegean provides the highest level of completeness at any given S/N, with a well-behaved decline in reliability below S/N
![]() $\sim 5-6$
. At the other end of the scale, Selavy has the lowest level of completeness at any S/N, but the best reliability (fewest false detections).
$\sim 5-6$
. At the other end of the scale, Selavy has the lowest level of completeness at any S/N, but the best reliability (fewest false detections).
All SFs seem to miss some bright sources, with Selavy standing out as the poorest in this regard. This is likely due in part to the handling of overlapping sources. Both PyBDSF and ProFound report the largest numbers of false sources (seen in
![]() $\mathcal{R_D}$
and
$\mathcal{R_D}$
and
![]() $\mathcal{R_S}$
) at high S/N. For PyBDSF this is a consequence of overestimating source sizes (Fig. 14), especially in the presence of closely neighbouring sources, or nearby noise spikes, by quite significant amounts in some cases (see Paper II). For ProFound this arises due to the blending of neighbouring sources (see Paper II).
$\mathcal{R_S}$
) at high S/N. For PyBDSF this is a consequence of overestimating source sizes (Fig. 14), especially in the presence of closely neighbouring sources, or nearby noise spikes, by quite significant amounts in some cases (see Paper II). For ProFound this arises due to the blending of neighbouring sources (see Paper II).
For EXT sources there is generally poorer performance overall compared to those for the CMP sources, most clearly seen in the
![]() $\mathcal{D}$
-image results (Fig. 15). There are also several artefacts appearing at unphysically low S/N (
$\mathcal{D}$
-image results (Fig. 15). There are also several artefacts appearing at unphysically low S/N (
![]() $\mbox{S/N}<1$
) arising from spurious faint detections. Even at reasonable S/N (
$\mbox{S/N}<1$
) arising from spurious faint detections. Even at reasonable S/N (
![]() $10<\mbox{S/N}<100$
) there is measurable incompleteness, and reliability that dips as low as 80% for some SFs. Here Aegean appears to perform the best, with Selavy showing much poorer performance.
$10<\mbox{S/N}<100$
) there is measurable incompleteness, and reliability that dips as low as 80% for some SFs. Here Aegean appears to perform the best, with Selavy showing much poorer performance.
5.3.2. Metrics for real sources
Fig. 17(a) and (b) show
![]() $\mathcal{C_{DS}}$
vs S/N and
$\mathcal{C_{DS}}$
vs S/N and
![]() $\mathcal{R_{DS}}$
vs S/N, respectively, for CMP sources. As we know what the true sources are, we can explore the validity of
$\mathcal{R_{DS}}$
vs S/N, respectively, for CMP sources. As we know what the true sources are, we can explore the validity of
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
by removing any false detections in the
$\mathcal{R_{DS}}$
by removing any false detections in the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-images, that is, we can compute
$\mathcal{S}$
-images, that is, we can compute
![]() $\mathcal{\tilde{C}_{DS}}$
(Equation (11)) and
$\mathcal{\tilde{C}_{DS}}$
(Equation (11)) and
![]() $\mathcal{\tilde{R}_{DS}}$
(Equation (12)). The results are shown in Fig. 17(c) and (d), respectively.
$\mathcal{\tilde{R}_{DS}}$
(Equation (12)). The results are shown in Fig. 17(c) and (d), respectively.

Figure 17.
![]() $\mathcal{C_{DS}}$
(a and g),
$\mathcal{C_{DS}}$
(a and g),
![]() $\mathcal{R_{DS}}$
(b and h),
$\mathcal{R_{DS}}$
(b and h),
![]() $\mathcal{\tilde{C}_{DS}}$
(c and i),
$\mathcal{\tilde{C}_{DS}}$
(c and i),
![]() $\mathcal{\tilde{R}_{DS}}$
(d and j),
$\mathcal{\tilde{R}_{DS}}$
(d and j),
![]() $\delta\mathcal{C_{DS}}$
(e and k), and
$\delta\mathcal{C_{DS}}$
(e and k), and
![]() $\delta\mathcal{R_{DS}}$
(f and l) vs S/N for CMP (top set) and simulated-extend (bottom set) sources. The S/N are expressed as
$\delta\mathcal{R_{DS}}$
(f and l) vs S/N for CMP (top set) and simulated-extend (bottom set) sources. The S/N are expressed as
![]() $\mathcal{D}$
-signal/
$\mathcal{D}$
-signal/
![]() $\mathcal{S}$
-noise and
$\mathcal{S}$
-noise and
![]() $\mathcal{S}$
-signal/
$\mathcal{S}$
-signal/
![]() $\mathcal{S}$
-noise for completeness and reliability, respectively, where the
$\mathcal{S}$
-noise for completeness and reliability, respectively, where the
![]() $\mathcal{S}$
-noise is computed using bane.
$\mathcal{S}$
-noise is computed using bane.
Comparing
![]() $\mathcal{\tilde{C}_{DS}}$
and
$\mathcal{\tilde{C}_{DS}}$
and
![]() $\mathcal{\tilde{R}_{DS}}$
with
$\mathcal{\tilde{R}_{DS}}$
with
![]() $\mathcal{C}_{\mathcal{DS}}$
and
$\mathcal{C}_{\mathcal{DS}}$
and
![]() $\mathcal{R}_{\mathcal{DS}}$
, respectively,
$\mathcal{R}_{\mathcal{DS}}$
, respectively,
![]() $\tilde{\mathcal{C}}_{\mathcal{DS}}$
is largely unchanged, while
$\tilde{\mathcal{C}}_{\mathcal{DS}}$
is largely unchanged, while
![]() $\tilde{\mathcal{R}}_{\mathcal{DS}}$
does not show the dip in
$\tilde{\mathcal{R}}_{\mathcal{DS}}$
does not show the dip in
![]() $\mathcal{R}_{\mathcal{DS}}$
around S/N
$\mathcal{R}_{\mathcal{DS}}$
around S/N
![]() $\sim$
10 seen for most SFs. It also excludes the decline seen by Aegean at low S/N. This suggests that the apparently poorer estimated reliability in
$\sim$
10 seen for most SFs. It also excludes the decline seen by Aegean at low S/N. This suggests that the apparently poorer estimated reliability in
![]() $\mathcal{R}_{\mathcal{DS}}$
arises from the existence of spurious sources detected in the
$\mathcal{R}_{\mathcal{DS}}$
arises from the existence of spurious sources detected in the
![]() $\mathcal{D}$
-image that are (not surprisingly) missed in the
$\mathcal{D}$
-image that are (not surprisingly) missed in the
![]() $\mathcal{S}$
-image.
$\mathcal{S}$
-image.
To quantify these results we define residuals between our unconstrained (
![]() $\mathcal{C}_{\mathcal{DS}}$
and
$\mathcal{C}_{\mathcal{DS}}$
and
![]() $\mathcal{R}_{\mathcal{DS}}$
) and constrained (
$\mathcal{R}_{\mathcal{DS}}$
) and constrained (
![]() $\mathcal{\tilde{C}_{DS}}$
and
$\mathcal{\tilde{C}_{DS}}$
and
![]() $\mathcal{\tilde{R}_{DS}}$
) metrics: that is, the residual completeness,
$\mathcal{\tilde{R}_{DS}}$
) metrics: that is, the residual completeness,
and residual reliability,
These quantities are shown in Fig. 17(e) and (f), respectively. In general, they are expected to be positive, as there should be an excess of false detections in
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
compared to
$\mathcal{R_{DS}}$
compared to
![]() $\mathcal{\tilde{C}_{DS}}$
and
$\mathcal{\tilde{C}_{DS}}$
and
![]() $\mathcal{\tilde{R}_{DS}}$
, by construction. Negative values may appear when real input sources are detected but poorly fit, leading to inconsistent flux densities between the
$\mathcal{\tilde{R}_{DS}}$
, by construction. Negative values may appear when real input sources are detected but poorly fit, leading to inconsistent flux densities between the
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{S}$
-images. The figure shows
$\mathcal{S}$
-images. The figure shows
![]() $\delta\mathcal{C_{DS}}$
predominantly highlighting a small number of spurious PyBDSF detections, and
$\delta\mathcal{C_{DS}}$
predominantly highlighting a small number of spurious PyBDSF detections, and
![]() $\delta\mathcal{R_{DS}}$
emphasising the distribution in S/N of the false detections.
$\delta\mathcal{R_{DS}}$
emphasising the distribution in S/N of the false detections.
Recognising these limitations, while also noting that for several SFs
![]() $\delta\mathcal{C_{DS}}$
and
$\delta\mathcal{C_{DS}}$
and
![]() $\delta\mathcal{R_{DS}}$
are small, the approach of estimating completeness and reliability for a given finder based on real images is not unreasonable. Clearly it is not as robust as doing so using known injected sources as a reference, but it may be a useful addition to analyses comparing finder performance on real data containing imaging artefacts and other hard to simulate systematics. Similar conclusions can be drawn for the EXT source case (Fig. 17(g) through (l)).
$\delta\mathcal{R_{DS}}$
are small, the approach of estimating completeness and reliability for a given finder based on real images is not unreasonable. Clearly it is not as robust as doing so using known injected sources as a reference, but it may be a useful addition to analyses comparing finder performance on real data containing imaging artefacts and other hard to simulate systematics. Similar conclusions can be drawn for the EXT source case (Fig. 17(g) through (l)).
Finally, we note that
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
in Fig. 17(a) and (b), respectively, for CMP sources fare much better than their EXT counterparts, (g) and (h), respectively. The metrics in the latter case perform even more poorly than their
$\mathcal{R_{DS}}$
in Fig. 17(a) and (b), respectively, for CMP sources fare much better than their EXT counterparts, (g) and (h), respectively. The metrics in the latter case perform even more poorly than their
![]() $\mathcal{C_{D}}$
,
$\mathcal{C_{D}}$
,
![]() $\mathcal{R_{D}}$
,
$\mathcal{R_{D}}$
,
![]() $\mathcal{C_{S}}$
, and
$\mathcal{C_{S}}$
, and
![]() $\mathcal{R_{S}}$
counterparts (Figs. 15 and 16). This could perhaps be due to confusion, given the source density (Fig. 12) and high MADFM statistics (Table 7).
$\mathcal{R_{S}}$
counterparts (Figs. 15 and 16). This could perhaps be due to confusion, given the source density (Fig. 12) and high MADFM statistics (Table 7).
5.4. Summary of validation tests
The Hydra software was tested using the Aegean, Caesar, ProFound, PyBDSF, and Selavy SFs, comparing them by first minimising the FDR based on a 90% PRD cutoff, through Typhon. This process was done for
![]() $2^\circ\times2^\circ$
CMP and EXT
$2^\circ\times2^\circ$
CMP and EXT
![]() $\mathcal{D/S}$
-images. The RMS box, MADFM, and source detection statistics were also shown to be consistent with the simulated data, thus validating Hydra’s performance. The source size distributions also provided an indication of its performance.
$\mathcal{D/S}$
-images. The RMS box, MADFM, and source detection statistics were also shown to be consistent with the simulated data, thus validating Hydra’s performance. The source size distributions also provided an indication of its performance.
The simulated data was used to develop
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
metrics for deep/shallow image pairs, treating
$\mathcal{R_{DS}}$
metrics for deep/shallow image pairs, treating
![]() $\mathcal{D}$
detections as true sources. This was done by examining these statistics with the erroneous detections filtered out, using knowledge of the underlying injected sources, leaving goodness of completeness,
$\mathcal{D}$
detections as true sources. This was done by examining these statistics with the erroneous detections filtered out, using knowledge of the underlying injected sources, leaving goodness of completeness,
![]() $\mathcal{\tilde{C}_{DS}}$
, and goodness of reliability,
$\mathcal{\tilde{C}_{DS}}$
, and goodness of reliability,
![]() $\mathcal{\tilde{R}_{DS}}$
, metrics. Contrasting
$\mathcal{\tilde{R}_{DS}}$
, metrics. Contrasting
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
with
$\mathcal{R_{DS}}$
with
![]() $\mathcal{C_D}$
(or
$\mathcal{C_D}$
(or
![]() $\mathcal{C_S}$
) and
$\mathcal{C_S}$
) and
![]() $\mathcal{R_D}$
(or
$\mathcal{R_D}$
(or
![]() $\mathcal{R_S}$
), respectively, a notable degradation in the former was observed for EXT images, most likely due to
$\mathcal{R_S}$
), respectively, a notable degradation in the former was observed for EXT images, most likely due to
![]() $\mathcal{DS}$
-confusion. That being said, in general, the form of
$\mathcal{DS}$
-confusion. That being said, in general, the form of
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
remains relatively unchanged, although the
$\mathcal{R_{DS}}$
remains relatively unchanged, although the
![]() $\mathcal{S}$
recovery rate,
$\mathcal{S}$
recovery rate,
![]() $\mathcal{S}\,:\,\mathcal{D}$
, is significantly reduced (Table 8). This suggests that these metrics are good for studying SF performance in real images, given the ability to quantify incompleteness (
$\mathcal{S}\,:\,\mathcal{D}$
, is significantly reduced (Table 8). This suggests that these metrics are good for studying SF performance in real images, given the ability to quantify incompleteness (
![]() $1-\mathcal{C}$
) and FDR (
$1-\mathcal{C}$
) and FDR (
![]() $1-\mathcal{R}$
).
$1-\mathcal{R}$
).
In passing, some observations of SF performance were also made, and are explored in more detail in Paper II. The source detection numbers were comparable between all SFs except for Selavy, which was consistently low (Table 8). Some variability in the residual RMS estimated for the
![]() $\mathcal{D}$
-mages was observed, with Selavy having unusually high values. For CMP sources the values were comparable except for Selavy, whereas for the EXT case there was significant variation except for Caesar and Profound. As for the
$\mathcal{D}$
-mages was observed, with Selavy having unusually high values. For CMP sources the values were comparable except for Selavy, whereas for the EXT case there was significant variation except for Caesar and Profound. As for the
![]() $\mathcal{S}$
-images the values were all consistent, except for Selavy being significantly high in the EXT source case. The MAFDM statistics were consistent in both cases for all SFs.
$\mathcal{S}$
-images the values were all consistent, except for Selavy being significantly high in the EXT source case. The MAFDM statistics were consistent in both cases for all SFs.
For CMP and EXT sources, Aegean had the best
![]() $\mathcal{C_D}$
(and
$\mathcal{C_D}$
(and
![]() $\mathcal{C_S}$
) statistics followed by PyBDSF, ProFound, Caesar, and Selavy. Selavy, followed to a lesser degree by Caesar, tends to miss bright sources, more so than the other SFs. For
$\mathcal{C_S}$
) statistics followed by PyBDSF, ProFound, Caesar, and Selavy. Selavy, followed to a lesser degree by Caesar, tends to miss bright sources, more so than the other SFs. For
![]() $\mathcal{R_D}$
(and
$\mathcal{R_D}$
(and
![]() $\mathcal{R_S}$
) they also reported the largest number of false sources at high S/N. The quality of the
$\mathcal{R_S}$
) they also reported the largest number of false sources at high S/N. The quality of the
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{R}$
statistics is poorer for EXT than CMP sources which is mainly attributed to confusion (see Fig. 12).
$\mathcal{R}$
statistics is poorer for EXT than CMP sources which is mainly attributed to confusion (see Fig. 12).
6. Conclusions
Radio astronomy has dramatically progressed in the lead-up to the SKA era (see, e.g., Fig. 1 of Norris et al. Reference Norris2021). The past decades have seen development of technologies and facilities that improve the survey speed, survey depth, and a rapid growth in results from SKA precursors. Ongoing and planned surveys such as VLASS (Lacy et al. Reference Lacy2020; Gordon et al. Reference Gordon2021) with 82% sky-coverage, and EMU (Norris et al. Reference Norris2011, Reference Norris2021) with 75% sky-coverage, expect to produce catalogues with source numbers into the millions and tens of millions.
Increasing survey sizes drive a need for SF software with highly robust and well-characterised completeness and reliability statistics. This need has driven source-finding challenges (e.g., Hopkins et al. Reference Hopkins2015; Bonaldi et al. Reference Bonaldi2021) for comparing the various tools and technologies. Some optical SFs have also been applied to radio images, such as SExtractor (Bertin & Arnouts Reference Bertin and Arnouts1996) and ProFound (Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019). Caesar was introduced for handling compact sources jointly with diffuse emission (Umana et al. Reference Umana2015), through the reprocessing of its residual image (Riggi et al. Reference Riggi2016). These are atural extensions of traditional thinking on radio source extraction. Qualitatively different approaches are also being developed, including the application of machine learning to this field (e.g., Bonaldi et al. Reference Bonaldi2021; D. Magro et al., in preparation). In the SKA era, it may be that source detection and cataloguing will need to be done on the fly due to the data volume (Bonaldi et al. Reference Bonaldi2021). A Hydra-like tool may have substantial value in that context, encapsulating the strengths of multiple SFs run in parallel.
The optimum comparison between SFs requires the expertise of the originators to fine tune their performance for a given set of reference images, as pursued in such data challenges. For this reason it is necessary to fairly compare large numbers of SFs on an even footing. Hydra was developed to encapsulate this expertise, in a modular fashion, using Docker containers. Hydra is extensible and the user does not have to be an expert at every SF to use it. Hydra focuses specifically on optimising the RMS threshold and island growth parameters, common to the traditional class of SFs, through the percentage real detections metric, PRD (Equation (1)). This two-parameter optimisation technique is adopted following Hale et al. (Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), who did the optimisation by hand, in a study comparing Aegean, ProFound, and PyBDSF. Hydra also includes an optional background-estimation optimisation step to identify the RMS box and step size parameters, through the mean noise metric,
![]() $\mu$
(Equation (3)). It is clearly possible to improve Hydra in order to handle more SF-specific parameters.
$\mu$
(Equation (3)). It is clearly possible to improve Hydra in order to handle more SF-specific parameters.
Hydra provides deep (
![]() $\mathcal{D}$
, i.e the input image) and shallow (
$\mathcal{D}$
, i.e the input image) and shallow (
![]() $\mathcal{S}$
, i.e., the D-image with
$\mathcal{S}$
, i.e., the D-image with
![]() $5\sigma$
noise added) catalogues for each SF, which are linked through a cluster table of overlapping components, or clumps (Fig. 5). The
$5\sigma$
noise added) catalogues for each SF, which are linked through a cluster table of overlapping components, or clumps (Fig. 5). The
![]() $\mathcal{S}$
-image creation and analysis is motivated by a desire to assess a given finder’s performance against itself, in the absence of simulated data, treating the
$\mathcal{S}$
-image creation and analysis is motivated by a desire to assess a given finder’s performance against itself, in the absence of simulated data, treating the
![]() $\mathcal{D}$
-image version of the SF’s catalogue as the ground truth. Each clump has an ID which can be used to locate the associated
$\mathcal{D}$
-image version of the SF’s catalogue as the ground truth. Each clump has an ID which can be used to locate the associated
![]() $\mathcal{D/S}$
-image and residual cutouts (with and without component annotations).
$\mathcal{D/S}$
-image and residual cutouts (with and without component annotations).
![]() $\mathcal{D/S}$
region files for the full images are also available. Hydra also merges catalogues of known sources (simulated in our case), providing corresponding metrics such as completeness (
$\mathcal{D/S}$
region files for the full images are also available. Hydra also merges catalogues of known sources (simulated in our case), providing corresponding metrics such as completeness (
![]() $\mathcal{C}$
) and reliability (
$\mathcal{C}$
) and reliability (
![]() $\mathcal{R}$
). Hydra also comes with an HTML viewer that allows the user to explore the various data products (Fig. 7).
$\mathcal{R}$
). Hydra also comes with an HTML viewer that allows the user to explore the various data products (Fig. 7).
This paper is part one of a two part series, in which we have introduced the Hydra software, and validated its optimisation algorithms, using simulated-compact (CMP) and simulated-extended (EXT) image data. In addition to the traditional
![]() $\mathcal{D}$
-image metrics, such as completeness (
$\mathcal{D}$
-image metrics, such as completeness (
![]() $\mathcal{C_D}$
) and reliability (
$\mathcal{C_D}$
) and reliability (
![]() $\mathcal{R_D}$
), Hydra introduces a whole new set of metrics, such as
$\mathcal{R_D}$
), Hydra introduces a whole new set of metrics, such as
![]() $\mathcal{S}$
-image completeness (
$\mathcal{S}$
-image completeness (
![]() $\mathcal{C_S}$
) and reliability (
$\mathcal{C_S}$
) and reliability (
![]() $\mathcal{R_S}$
), and
$\mathcal{R_S}$
), and
![]() $\mathcal{DS}$
-image completeness (
$\mathcal{DS}$
-image completeness (
![]() $\mathcal{C_{DS}}$
) and reliability (
$\mathcal{C_{DS}}$
) and reliability (
![]() $\mathcal{R_{DS}}$
), respectively. In this paper we also validated the
$\mathcal{R_{DS}}$
), respectively. In this paper we also validated the
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
metrics for use with real images, by using our simulated data where the true sources are known. It was found that
$\mathcal{R_{DS}}$
metrics for use with real images, by using our simulated data where the true sources are known. It was found that
![]() $\mathcal{C_{DS}}$
and
$\mathcal{C_{DS}}$
and
![]() $\mathcal{R_{DS}}$
are useful for characterising SF performance, provided one keeps in mind the
$\mathcal{R_{DS}}$
are useful for characterising SF performance, provided one keeps in mind the
![]() $\mathcal{D}$
detections are incomplete with a slight degradation in
$\mathcal{D}$
detections are incomplete with a slight degradation in
![]() $\mathcal{R_{DS}}$
for low S/N. In Paper II we evaluate the performance of the SFs using our simulated images along with real data.
$\mathcal{R_{DS}}$
for low S/N. In Paper II we evaluate the performance of the SFs using our simulated images along with real data.
Acknowledgements
M. M. Boyce, S. A. Baum, Y. A. Gordon, D. Leahy, C. O’Dea, and A. N. Vantyghem acknowledge partial support from the NSERC of Canada. S. Riggi acknowledges INAF for financial support through the PRIN TEC programme ‘CIRASA.’ Partial support for L. Rudnick came from U.S. National Science Foundation Grant AST17-14205 to the University of Minnesota. M. I. Ramsay acknowledges support from NSERC and the University of Manitoba Faculty of Science Undergraduate Research Award (USRA). C. L. Hale acknowledges support from the Leverhulme Trust through an Early Career Research Fellowship. Y. A. Gordon is supported by US National Science Foundation grant 2009441. H. Andernach benefited from grant CIIC 138/2020 of Universidad de Guanajuato, Mexico. D. Leahy acknowledges support from NSERC 10020476. M. J. Michaowski acknowledges the support of the National Science Centre, Poland through the SONATA BIS grant 2018/30/E/ST9/00208. S. Safi-Harb acknowledges support from NSERC through the Discovery Grants and the Canada Research Chairs programs, and from the Canadian Space Agency. M. Vaccari acknowledges financial support from the Inter-University Institute for Data Intensive Astronomy (IDIA), a partnership of the University of Cape Town, the University of Pretoria, the University of the Western Cape and the South African Radio Astronomy Observatory, and from the South African Department of Science and Innovation’s National Research Foundation under the ISARP RADIOSKY2020 Joint Research Scheme (DSI-NRF Grant Number 113121) and the CSUR HIPPO Project (DSI-NRF Grant Number 121291). E. L. Alexander gratefully acknowledges support from the UK Alan Turing Institute under grant reference EP/V030302/1 and from the UK Science & Technology Facilities Council (STFC) under grant reference ST/P000649/1. A. S. G. Robotham acknowledges support via the Australian Research Council Future Fellowship Scheme (FT200100375). H. Tang greatfully acknowledges the support from the Shuimu Tsinghua Scholar Program of Tsinghua University, the fellowship of China Postdoctoral Science Foundation 2022M721875, and long lasting support from JBCA machine learning group and Doa Tsinghua machine learning group.
Hydra is written primarily in Python, with some elements of Cython (Behnel et al. Reference Behnel, Bradshaw, Citro, Dalcin, Seljebotn and Smith2011) and R, along with their standard libraries. Hydra uses alphashape (Bellock, Godber, & Philip Reference Bellock, Godber and Philip2021), APLpy (Robitaille & Bressert Reference Robitaille and Bressert2012), Astropy (Astropy Collaboration et al. Reference Astropy Collaboration2013, Reference Astropy Collaboration2018), Matplotlib (Hunter Reference Hunter2007), NumPy (Harris et al. Reference Harris2020), and pandas (McKinney Reference McKinney, van der Walt and Millman2010; Pandas Development Team 2020) Python libraries commonly used in astronomy. Hydra utilises click, gzip, Jinja, tarfile, and YAML Python libraries as part its overall architectural infrastructure. Hydra encapsulates Aegean (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012, Reference Hancock, Cathryn and Hurley-Walker2018), Caesar (Riggi et al. Reference Riggi2016, Reference Riggi2019), ProFound (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018; Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019), PyBDSF (Mohan & Rafferty Reference Mohan and Rafferty2015), and Selavy (Whiting & Humphreys Reference Whiting and Humphreys2012) source finder software using Docker. The technical diagrams in this paper we created using macOS Preview and Microsoft PowerPoint. We acknowledge the authors of the aforementioned software applications, languages, and libraries.
M. M. Boyce would like to thank T. Galvin for discussions regarding clustering techniques (re. Section 3.1.4) and extending these concepts to potential computational geometry applications (re., Edelsbrunner Reference Edelsbrunner2013) in multiwavelength astronomy.
CIRADA is funded by a grant from the Canada Foundation for Innovation 2017 Innovation Fund (Project 35999) and by the Provinces of Ontario, British Columbia, Alberta, Manitoba and Quebec, in collaboration with the National Research Council of Canada, the US National Radio Astronomy Observatory and Australia’s Commonwealth Scientific and Industrial Research Organisation.
The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
ASKAP is part of the ATNF which is managed by the CSIRO. Operation of ASKAP is funded by the Australian Government with support from the National Collaborative Research Infrastructure Strategy. ASKAP uses the resources of the Pawsey Supercomputing Centre. Establishment of ASKAP, the Murchison Radio Astronomy Observatory and the Pawsey Supercomputing Centre are initiatives of the Australian Government, with support from the Government of Western Australia and the Science and Industry Endowment Fund. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site.
Data Availability
Hydra is available, along with the data products presented in this paper, by navigating through the CIRADA portal at https://cirada.ca.
Appendix A. Cerberus Code Template Notes
In this appendix we provide more architectural details regarding Cerberus template rules discussed in Section 3.1.2. The intent here is to provide enough detail to give an overall sense of Hydra’s extensible nature. Further details can be found in the Hydra user manual.
Fig. A.1. shows a more detailed view of the Cerberus code generation workflow (c.f., Fig. 3). The term ‘template’ refers to the overall directory hierarchy, configuration files, and naming conventions. At the lowest level, within the config directory, are subdirectories for each of the SFs, containing *.py and/or *.R script files, *.dcr Dockerfiles, and *.yml YAML files. The docker-compose.yml and config.yml files in the main config directory provide the glue for building containers and code generation, respectively.

Figure A.1. Detailed breakdown of the Cerberus code generation workflow given in Fig. 3. Fig. A.2 shows a detailed example of an Aegean container image build, utilising aegean.dcr, aegean.py, and docker-compose.yml. Fig. A.3 shows an example of updating cerberus.py to include Aegean, through code generation, utilising aegean.yml and config.yml. All of the information in Configuration Management is accessible to all of the tools within the Hydra software suite.

Figure A.2. Example of Aegean containerisation. The Dockerfile, aegean.dcr, has four main parts, (1) a base Ubuntu 20.04 operating system, (2) an AegeanTools toolbox build environment, (3) a home_dir, input_dir, processing_dir, and output_dir directory structure along with a local script, aegean.py, and (4) an ENTRYPOINT (EP) through which aegean.py can be externally accessed by cerberus.py. The docker-compose.yml configuration file contains an Aegean build block (aegean:), which has two main parts, (1) a part defining the image name (aegean) along with a pointer the Dockerfile (aegean/aegean.dcr), and (2) a part containing the directory file structure to be built along with a pointer to aegean.py. The container image is built, using this information, with the docker-compose command.
A.1. Containerisation
The general recipe for containerising SFs is as follows.
• Create a Docker build file containing the following:
– Base operating system environment
– SF environment with tools
– SF wrapper script with command-line arguments:
* Input image path
* Processing directory path
* Output directory path
* Image filename to process
* RMS-Parameter with default setting
* Island-Parameter with default setting
* RMS box parameters (optional)
* FITS catalogue file output flag (default, CSV)
* Residual image flag
* Dump flag
* Help flag
– Internal directory structure:
* Script home directoryFootnote s
-
 $\cdot\ $
Input subdirectory
$\cdot\ $
Input subdirectory -
 $\cdot\ $
Processing subdirectory
$\cdot\ $
Processing subdirectory -
 $\cdot\ $
Results subdirectory
$\cdot\ $
Results subdirectory
– A container ENTRYPOINT
• Update the docker-compose.yml configuration file with the container build instructions
• Build the container image
The input and output directories serve as external mount points, used by the cerberus.py wrapper script: that is, the input directory contains the input image, the processing directory contains the SF wrapper script scratch files, and the results directory contains output catalogues, region files, etc.Footnote t The container ENTRYPOINT allows cerberus.py external access to the internal script. Aegean is perhaps one of the simplest SFs to containerise, with details shown in Fig. A.2.
As can be seen, Aegean comes as part of an AegeanTools toolbox within an Ubuntu 20.04 operating system. The Dockerfile, container directory structure, and local aegean.py container wrapper script are defined in the docker-compose.yml configuration file. Everything related to Aegean containers, directories, scripts, etc., are all prefixed with aegean. Also, aegean.py can be accessed internally within the container, for example,

or externally outside of the container, that is,
the latter being used by cerberus.py (Section 3.1.2). After implementing the above template rules a new container image can be built using the docker-compose command within the config directory.
A.2. Code Generation
For code generation a metadata file needs to be created (e.g., aegean.yml), and then linked to the master configuration file, config.yml. This information is then used for code generation through the Jinja template engine. Fig. A.3 shows an example workflow for creating the Aegean module.

Figure A.3. Example of the addition of an Aegean module for cerberus.py through code generation. In short, the developer creates an aegean.yml metadata file and links it to the master configuration file, config.yml. Then by running the script_generator.py script, in the libs directory, the module is installed.
All scripts within the Hydra software suite have access to the Configuration Management system in order to perform operations in a generic fashion. For example, cerberus.py utilises the docker-compose configuration file for linking calls to the source-finder container images, typhon.py utilises the metadata files for parameters and constraints used for source-finder optimisation, hydra.py utilises the metadata files for catalogue processing, and so on.
B. Source Finder Implementation Notes
In this section we briefly overview the SFs currently supported by Hydra and their relevant settings.
It should be noted that Aegean, Caesar, and Selavy have various multiprocessor mode implementations wherein large images are split into manageable chunks and processed in parallel in order to reduce the overall processing time (see Hancock et al. Reference Hancock, Cathryn and Hurley-Walker2018; Riggi et al. Reference Riggi2019; Whiting & Humphreys Reference Whiting and Humphreys2012, respectively for details). For the current implementation of Hydra we have chosen to leave these modes disabled. These modes provide various methods for dealing with background noise computations and source detection, which become problematic near edges of sub-images, and consequently have tendencies to bias the statistics especially when comparing against non-multiprocessor SFs, such as ProFound and PyBDSF.
B.1. Aegean
The AegeanTools toolbox contains two main items of relevance to this discussion, a background and RMS noise computation script, bane, and a source finding script, Aegean (Hancock et al. Reference Hancock, Cathryn and Hurley-Walker2018). bane uses a sliding box-car method, with grid-based box and step size parameters, wherein RMS noise estimates are calculated using sigma-clipping. Aegean itself uses a faster, but less accurate, ‘zones’ algorithm. Aegean can also use the output from bane, which is the implementation adopted here.
The Aegean SF uses a flood-fill algorithm to identify islands above a detection threshold. It then implements a deblending process to determine the number of local maxima through the discrete 2D Laplacian (i.e., curvature) kernel
 \begin{equation} L^2_{xy}=\left[\begin{array}{c@{\quad}r@{\quad}c} 1 & 1 & 1 \\[3pt] 1 & -8 & 1 \\[3pt] 1 & 1 & 1 \end{array}\right]\,,\end{equation}
\begin{equation} L^2_{xy}=\left[\begin{array}{c@{\quad}r@{\quad}c} 1 & 1 & 1 \\[3pt] 1 & -8 & 1 \\[3pt] 1 & 1 & 1 \end{array}\right]\,,\end{equation}
to identify flux peaks for localised fitting of Gaussian components (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012). Its flood-fill algorithm utilises two parameters, a seed threshold parameter,
![]() $\sigma_s$
(i.e., seedclip), above which to seed an island, and a flood threshold parameter,
$\sigma_s$
(i.e., seedclip), above which to seed an island, and a flood threshold parameter,
![]() $\sigma_f$
(i.e., floodclip), above which to grow an island, such that,
$\sigma_f$
(i.e., floodclip), above which to grow an island, such that,
![]() $\sigma_s\ge\sigma_f$
(see Table 2). It then convolves the image with Equation (B1), producing a curvature map, from which it implements Gaussian fits to local depressions (i.e., negative curvature bowls, corresponding to local flux density maxima) within the islands.
$\sigma_s\ge\sigma_f$
(see Table 2). It then convolves the image with Equation (B1), producing a curvature map, from which it implements Gaussian fits to local depressions (i.e., negative curvature bowls, corresponding to local flux density maxima) within the islands.
The implementation of the Aegean (version 2.2.4) module for Cerberus provides the box-car and flood-fill parameters, as per module design requirements.
Here we use the source component catalogue: that is, source island information is not included in this version of Hydra.Footnote u Of particular interest are the integrated flux densities and fitted component sizes.
B.2. Caesar
Caesar does its source finding using a flood-fill method to obtain blobs (i.e., ‘islands’), from which child-blobs (or ‘nested blobs’) are (optionally) extracted using elliptical-Gaussian-based Laplacian (Equation (B1)) or
![]() $\chi^2$
filters (Riggi et al. Reference Riggi2016, Reference Riggi2019). Compact sources, that is, childless-blobs, are subtracted out to leave a residual map with extended sources that can be extracted either though a wavelet transform, saliency, hierarchical-clustering, or active-contour filter.
$\chi^2$
filters (Riggi et al. Reference Riggi2016, Reference Riggi2019). Compact sources, that is, childless-blobs, are subtracted out to leave a residual map with extended sources that can be extracted either though a wavelet transform, saliency, hierarchical-clustering, or active-contour filter.
The RMS and island parameters come in two sets, one for the parents, seedThr and mergeThr, respectively, and one for the children, nestedBlobPeakZThr and nestedBlobPeakZMergeThr, respectively. As we are optimising these parameters externally (through the PRD, Equation (1)), we set compactSourceSearchNIters = 1 to prevent decrements in seedThr by seedThrStep. In our implementation, we also search for child-blobs (i.e., searchNestedSources = true), with their RMS and island parameters set to the same values as their parents (Riggi et al. Reference Riggi2019). For child-blob filtering we use the Laplacian method (i.e., blobMaskMethod = 2, with fitSources = true), and for source extraction we use the saliency filter method (i.e., extendedSearchMethod = 2; for algorithms, see Riggi et al. Reference Riggi2016).
It should be noted here that searching for child-blobs is not necessary for an image consisting of only point sources; however, for consistency, we prefer to have the same settings for both point and extended sources, for the purposes of comparing performance against other SFs. The only potential impact of this approach is in extra processing time.
Caesar also does background and RMS noise optimisation through any of the following metrics,
![]() $\mu/\sigma$
, median/MADFM, biweight, and clipped median/
$\mu/\sigma$
, median/MADFM, biweight, and clipped median/
![]() $\sigma$
. Consequently it does not require pre-tuning like PyBSDF, for example. Here we have chosen the median/MADFM metric (i.e., bkgEstimator = 2, with useLocalBkg = true and useBeamInfoInBkg = true), as it is similar to the pre-optimisation scheme option used by Typhon.
$\sigma$
. Consequently it does not require pre-tuning like PyBSDF, for example. Here we have chosen the median/MADFM metric (i.e., bkgEstimator = 2, with useLocalBkg = true and useBeamInfoInBkg = true), as it is similar to the pre-optimisation scheme option used by Typhon.
Table B.1 summarises all of the internal settings of Cerberus’s Caesar module. Note that we have also set some of the residual image processing flags, so as to remove all source types (removedSourceType = -1) with the appropriate thresholding (i.e., residualZHighThr = seedThr and residualZThr = mergeThr).
Table B.1. Caesar (Version 1.1.5) module settings.

The output source components are obtained from the source component catalogue, that is, we do not include the source island catalogue in this version of Hydra. Of particular interest are the integrated flux densities and fitted component sizes.
B.3. ProFound
ProFound uses a watershed deblending process, wherein it systematically searches for the highest flux pixel and expands outwards and downwards in flux to some cutoff, creating a segment (i.e., ‘island’), before proceeding to the next highest flux pixel, and so on (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018). The end result is the formation of ‘flux-mountains’ (segments) with peaks and valleys (boundaries between segment groups). After the segments have been determined, it then dilates them until convergence is reached, as determined by a Kron/Petrosian-like dilation kernel (see Section 2), while assigning overlapping segment fluxes to the ones with the most flux (e.g., Fig. B.1). The segment formation threshold is determined by a skycut parameter, which corresponds to our RMS parameter, and the segment partitioning is determined by a tolerance parameter, which corresponds to our island parameter.

Figure B.1. Example of ProFound dilation process of a small
![]() $3^\prime\times3^\prime$
VLASS Epoch 1.1 Quick Look (QL) image cutout, centred at J222135+070712. The cutout was extracted from a QL image tile, available at NRAO (https://science.nrao.edu), and then processed using ProFound in R Studio.
$3^\prime\times3^\prime$
VLASS Epoch 1.1 Quick Look (QL) image cutout, centred at J222135+070712. The cutout was extracted from a QL image tile, available at NRAO (https://science.nrao.edu), and then processed using ProFound in R Studio.
ProFound was designed for optical images and so there are some nuances when it comes to applying it to radio image data (see Hale et al. Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019). Table B.2 summarises all of the settings internal to the ProFound module,Footnote v used herein. In addition, a considerable amount of wrapper code was required so as to extract the appropriate ‘radio catalogue like’ information from its internal hierarchical data structure. Of particular interest are the total flux density and component size, which are pixel sums and flux-weighted fits,Footnote w respectively, for a given segment (Robotham et al. Reference Robotham, Davies, Driver, Koushan, Taranu, Casura and Liske2018). Consequently these are not directly comparable to FWHM measurements from Gaussian fits in other SFs.
Table B.2 ProFound (version 1.13.1, with R version 4.0.3) module default settings, where box = c(100, 100). It should be noted that results can differ radically between versions of ProFound and R. Furthermore, the default settings mentioned in the documentation can differ considerably from what is actually in the source code. This table includes all settings that are deemed important for reproducing our results.

B.4. PyBDSF
PyBDSF identifies islands by collecting pixels greater than a given flux threshold, thresh_pix,Footnote x and then expands outwards from those pixels in octets above a given island-boundary threshold, thesh_isl. Our RMS and island parameters correspond to former and latter thresholds, respectively. After the islands have been determined, it performs multiple Gaussian fits to each island (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012).
We follow the same generic recipe as Hale et al. (Reference Hale, Robotham, Davies, Jarvis, Driver and Heywood2019) to accommodate extended sources, as outlined in Table B.3. The atrous_do parameter selects the à trous wavelet decomposition (Holschneider et al. Reference Holschneider, Kronland-Martinet, Morlet, Tchamitchian, Combes, Grossmann and Tchamitchian1989) module as one of several options for post-processing. These include shapelet decomposition, à trous wavelet decomposition, PSF variation, polarisation, and spectral index modules. Setting flag_maxsize_bm = 100 along with atrous_do = True allows for Gaussians greater than the beam size and of varying scales, respectively. Setting mean_map = “zero” sets the background mean to zero, enhancing the detection of extended emission.
Table B.3 PyBDSF (version 1.9.1) module settings.

The PyBDSF module also provides the rms_box tuple, so that the RMS box and step sizes can be optimised by Typhon.
The output source components are obtained from the source catalogue: that is, catalog_type = ’srl’ via the write_image(…) command. The catalogue does not include empty islands (i.e., incl_empty = False). Of particular interest are the total flux densities and component sizes, which are expressed as integrated Stokes I and FWHM’s, respectively.
B.5. Selavy
Selavy is a ‘single-pass’ raster-scan, or thresholding, type SF (see Lutz Reference Lutz1980), with Duchamp (Whiting Reference Whiting2012), a 3D SF, at its heart (Whiting & Humphreys Reference Whiting and Humphreys2012). Here we are interested in its 2D spatial search features (i.e., searchType = spatial). The algorithm works downwards by growing regions of detection through a threshold parameter (see Fig. 3 of Whiting & Humphreys Reference Whiting and Humphreys2012), snrCut, our RMS parameter, after which they can be further extended downwards and outwards through an optional growthCut parameter, our island parameter. Further post-processing options are available, such as producing components from multi-Gaussian fitting: that is, doFit = True, to turn the fitting option on, fitTypes = [full], to fit all degrees of freedom, and numGaussFromGuess = True, to provide an initial guess from the number of distinct peaks found within a given region during thresholding.Footnote y
Selavy also has various options for background estimates, such as typical
![]() $\mu$
/
$\mu$
/
![]() $\sigma$
or more robust median/MADFM based statistics (Whiting Reference Whiting2012). We use a variable sliding box method (VariableThreshold = True) with robust statistics (flagRobustStats = True) and Selavy.Variable Threshold.boxSize = (rms_box-1)/2, where rms_box is determined by Typhon.
$\sigma$
or more robust median/MADFM based statistics (Whiting Reference Whiting2012). We use a variable sliding box method (VariableThreshold = True) with robust statistics (flagRobustStats = True) and Selavy.Variable Threshold.boxSize = (rms_box-1)/2, where rms_box is determined by Typhon.
Table B.4 summarises all of the internal settings of Cerberus’s Selavy module.
The output source components are obtained from the source component catalogue: that is, we do not include the source island catalogue in this version of Hydra. Of particular interest are the integrated flux densities and fitted component sizes.
Table B.4. Selavy (version 1.1.0) module settings.