Published online by Cambridge University Press: 07 September 2023
The present work discusses the use of a weakly-supervised deep learning algorithm that reduces the cost of labelling pixel-level masks for complex radio galaxies with multiple components. The algorithm is trained on weak class-level labels of radio galaxies to get class activation maps (CAMs). The CAMs are further refined using an inter-pixel relations network (IRNet) to get instance segmentation masks over radio galaxies and the positions of their infrared hosts. We use data from the Australian Square Kilometre Array Pathfinder (ASKAP) telescope, specifically the Evolutionary Map of the Universe (EMU) Pilot Survey, which covered a sky area of 270 square degrees with an RMS sensitivity of 25–35 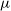 $\mu$Jy beam
$\mu$Jy beam $^{-1}$. We demonstrate that weakly-supervised deep learning algorithms can achieve high accuracy in predicting pixel-level information, including masks for the extended radio emission encapsulating all galaxy components and the positions of the infrared host galaxies. We evaluate the performance of our method using mean Average Precision (mAP) across multiple classes at a standard intersection over union (IoU) threshold of 0.5. We show that the model achieves a mAP
$^{-1}$. We demonstrate that weakly-supervised deep learning algorithms can achieve high accuracy in predicting pixel-level information, including masks for the extended radio emission encapsulating all galaxy components and the positions of the infrared host galaxies. We evaluate the performance of our method using mean Average Precision (mAP) across multiple classes at a standard intersection over union (IoU) threshold of 0.5. We show that the model achieves a mAP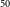 $_{50}$ of 67.5% and 76.8% for radio masks and infrared host positions, respectively. The network architecture can be found at the following link: https://github.com/Nikhel1/Gal-CAM
$_{50}$ of 67.5% and 76.8% for radio masks and infrared host positions, respectively. The network architecture can be found at the following link: https://github.com/Nikhel1/Gal-CAM
Permanent address: Depto. de Astronomía, DCNE, Universidad de Guanajuato, Guanajuato, CP, Mexico