2.2.1 M dwarfs

The M spectral classification has been recognised from the early days of astronomical spectroscopy. While most M dwarfs are stars, young objects of late M spectral types can be brown dwarfs (as shown in Figure 1). The modern classification scheme for M-dwarfs is based on that of Boeshaar (Reference Boeshaar1976) extended by Boeshaar & Tyson (Reference Boeshaar and Tyson1985) and Kirkpatrick, Henry & McCarthy (Reference Kirkpatrick, Henry and McCarthy1991) to spectral type M9.5. The Kirkpatrick et al. (Reference Kirkpatrick, Henry and McCarthy1991) spectral classification is based on the spectral region from 630–900 nm. The spectral standards chosen for late M types are listed in Table 1.

Table 1. Mean properties and spectral standards for late M to Y dwarfs

References. First reference is to adoption of the spectral standard, and the second reference is to the source of the mean absolute magitudes.

1. Kirkpatrick et al. (Reference Kirkpatrick, Henry and McCarthy1991), 2. Kirkpatrick et al. (Reference Kirkpatrick1999), 3. Kirkpatrick et al. (Reference Kirkpatrick2010) 4. Burgasser et al. (Reference Burgasser, Geballe, Leggett, Kirkpatrick and Golimowski2006a), 5. Cushing et al. (Reference Cushing2011), 6. Kirkpatrick et al. (Reference Kirkpatrick2012), 7. Dupuy & Liu (Reference Dupuy and Liu2012), 8. Dupuy & Kraus (Reference Dupuy and Kraus2013)

Notes.

Mean effective temperatures are from the data of Figure 6. Spectral standards are those adopted for optical classification up to spectral class L8, and for near-IR classification for L9 and later. Near-IR spectral standards for earlier types can be found in Kirkpatrick et al. (Reference Kirkpatrick2010). Spectral data is available for download for most of these objects (and other late-type dwarfs) at:

SpeX Prism Spectral Libraries (A. Burgasser)

— http://pono.ucsd.edu/~adam/browndwarfs/spexprism/

IRTF Spectral library (M.R. Cushing)

— http://irtfweb.ifa.hawaii.edu/~spex/IRTF_Spectral_Library/

L and T dwarf data archive (S.K. Leggett)

— http://staff.gemini.edu/~sleggett/LTdata.html

NIRSPEC Brown Dwarf Spectroscopic Survey (I.S. McLean)

— http://www.astro.ucla.edu/~mclean/BDSSarchive

Keck LRIS specra of late-M, L and T dwarfs (I.N. Reid)

— http://www.stsci.edu/~inr/ultracool.html

The M spectral class is characterised by the presence of bands of TiO and VO. TiO bands increase in strength up to spectral type M6, and VO becomes strong in the latest types.

In the near infrared (near-IR) M dwarfs show broad absorptions due to H₂O centred around 1.4 and 1.9 μm increasing in strength with later spectral types. Late M dwarfs also show Na I and K I absorptions in the 1.15–1.25 μm region. FeH absorption is present in the Wing-Ford band at 1 μm as well as the E-A band in the 1.6 μm region (Hargreaves et al. Reference Hargreaves, Hinkle, Bauschlicher, Wende, Seifahrt and Bernath2010). CO absorption is present at 2.3 μm.

2.2.2 L dwarfs

The L dwarf class is disinguished by the weakening and disappearance of the TiO and VO bands that are distinctive of M dwarfs. TiO has disappeared by L6 and VO by L4. A classification scheme for L dwarfs based on the optical spectral region (630–1000 nm) is described by Kirkpatrick et al. (Reference Kirkpatrick1999). It lists spectral standards for classes L0 to L8 (see Table 1) and classification is based on the weakening TiO and VO bands, changes in CrH and FeH bands (CrH is strongest at L5) and the alkali metals, with Cs I and Rb I lines increasing in strength to later types.

Spectral classification of L dwarfs in the near-IR is discussed by Reid et al. (Reference Reid, Burgasser, Cruz, Kirkpatrick and Gizis2001), Geballe et al. (Reference Geballe2002) and Nakajima, Tsuji, & Yanagisawa (Reference Nakajima, Tsuji and Yanagisawa2004). Kirkpatrick et al. (Reference Kirkpatrick2010) defined a set of spectral standards for the near-IR for spectral types M0 – L9. The near-IR region shows broad absorption bands of H₂O increasing in strength towards later spectral types.

While methane in the 1–2.5 μm region is not seen until spectral type T, the stronger methane ν₃ band in the 3.3 μm region is observable in late L dwarfs (Noll et al. Reference Noll, Geballe, Leggett and Marley2000; Schweitzer et al. Reference Schweitzer, Gizis, Hauschildt, Allard, Howard and Kirkpatrick2002; Stephens et al. Reference Stephens2009).

The physical basis for the M-L transition is thought to be the formation of condensates. At temperatures just below 2000 K the condensation of Ti bearing species such as CaTiO₃ (perskovite) and Ti₂O₃ removes TiO from the gas phase, and at slightly lower temperatures VO condenses as solid VO (Burrows & Sharp Reference Burrows and Sharp1999; Lodders Reference Lodders2002). Species such as enstatite (MgSiO₃), forsterite (Mg₂SiO₄), spinel (MgAl₂O₄) and solid iron also condense and these produce the dust clouds that are necessary to explain the spectra and colours of L dwarfs (Allard et al. Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001; Marley et al. Reference Marley, Seager, Saumon, Lodders, Ackerman, Freedman and Fan2002; Tsuji Reference Tsuji2002)

2.2.3 T dwarfs

The T dwarf class is characterised by the appearance of methane (CH₄) absorption features in the near-IR region (1–2.5 μm) . Methane first becomes apparent in early T dwarfs due to features at 1.67 and 2.2 μm which represent the Q-branches of the strongest methane bands 2ν₃ at 1.67 μm and ν₂ + ν₃ at 2.2 μm. This is accompanied by weakening of the CO absorption at 2.3 μm.

At later types broad methane absorptions develop due to the complex methane band systems, the octad (8 ground-state bands in the 2.1–2.4 μm region; Hilico et al. Reference Hilico, Robert, Loete, Tuomi, Pine and Brown2001) and the tetradecad (14 ground-state bands in the 1.6–2.0 μm region; Nikitin et al. Reference Nikitin, Boudon, Wenger, Albert, Brown, Baurecker and Quack2013a). These ground-state bands are associated with large numbers of hot bands. Methane absorption is also present at around 1.4 μm (the icosad – 20 ground-state bands) and 1.15 μm (the triacontad – 30 ground-state bands). Bailey, Ahlsved, & Meadows (Reference Bailey, Ahlsved and Meadows2011) provides a more detailed description of the methane spectrum.

In late T dwarfs the broad CH₄ and H₂O absorptions deepen and combine to leave a spectrum defined by approximately triangular peaks at 1.08 μm, 1.27 μm and 1.58 μ (the ‘windows’ between the deep absorptions), as well as a weaker peak at about 2.1 μm. T dwarf spectra are also shaped by the collision-induced absorption due to H₂ – H₂ pairs (Borysow Reference Borysow2002; Abel et al. Reference Abel, Frommhold, Li and Hunt2011) which depresses the 2 μm peak, and by the far wings of very strong Na I and K I lines in the optical (Burrows & Volobuyev Reference Burrows and Volobuyev2003; Allard et al. Reference Allard, Allard, Hauschildt, Kielkopf and Machin2003) which absorb at wavelengths up to ~ 1 μm.

Classification schemes for T dwarfs based on near-IR spectra, were developed by Burgasser et al. (Reference Burgasser2002) and Geballe et al. (Reference Geballe2002) and the two schemes were unified in Burgasser et al. (Reference Burgasser, Geballe, Leggett, Kirkpatrick and Golimowski2006a). That work gives a set of spectral standards for T0–T8 (see Table 1). The main features used for classification are the increasing depths of the H₂O and CH₄ bands towards later classes. A parallel optical classification scheme based on the 630–1010 nm region is described by Burgasser et al. (Reference Burgasser, Kirkpatrick, Liebert and Burrows2003) and is based on some of the same spectral standards used in the near-IR.

The transition from L to T is associated with the switch in chemical equlibirum between CO and CH₄ (Lodders Reference Lodders2002; Burrows & Sharp Reference Burrows and Sharp1999) that occurs at about 1400 K at 1 bar pressure, with CO being more stable above this temperature, and CH₄ being favoured at lower temperatures. However, the transition is also associated with a clearing of the dust clouds that are important in L dwarfs (Allard et al. Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001; Burgasser et al. Reference Burgasser2002).

2.2.4 Y dwarfs

The possible existence of objects even cooler than the T dwarfs was investigated in models by Burrows, Sudarsky, & Lunine (Reference Burrows, Sudarsky and Lunine2003). Among the features suggested as marking the transition to a new spectral class, were the appearance of NH₃ absorption, the condensation of H₂O clouds, and the development of redder near-IR colours reversing the trend in T dwarfs. A number of of very cool dwarfs were found in the CFBDS and UKIDSS surveys (Warren et al. Reference Warren2007; Delorme et al. Reference Delorme2008b; Burningham et al. Reference Burningham2008). Lucas et al. (Reference Lucas2010) reported the discovery of an even cooler object UGPS 0722 − 05 which they suggested should be classified as T10, and could in the future be regarded as the first example of a new spectral type.

In 2011, Cushing et al. (Reference Cushing2011) reported the ‘Discovery of Y-dwarfs’. Several objects identified using the WISE satellite were found to be of later spectral types than UGPS 0722 − 05. They reclassified UGPS 0722 − 05 as the T9 spectral standard, and classified six new objects as Y dwarfs with WISE 1738+27 as the Y0 standard. Kirkpatrick et al. (Reference Kirkpatrick2012) report several more Y dwarfs and added a spectral standard for the Y1 class (see Table 1). Other reported Y dwarfs are WISE J1639 − 68 (Tinney et al. Reference Tinney, Faherty, Kirkpatrick, Wright, Gelino, Cushing, Griffith and Salter2012) and the white dwarf companion WD 0806 − 661 B (Luhman, Burgasser, & Bochanski Reference Luhman, Burgasser and Bochanski2011; Luhman et al. Reference Luhman, Burgasser, Labbé, Saumon, Marley, Bochanski, Monson and Pearson2012). The high proper motion object WISE J085 510.83 − 071 442.5 (Luhman Reference Luhman2014) has absolute magnitude and colours suggesting it is the coolest known Y dwarf with an effective temperature of 225 – 260 K.

All Y dwarfs are very faint objects (J mag of 19 or fainter) and so the quality of available spectra are limited. They resemble the late T dwarfs, but the ‘window’ features (particularly that at 1.27 μm) become increasingly narrow with later spectral types. The NH₃ absorptions expected at ~ 1.53 and ~ 1.03 μm are not seen at the levels predicted by equilibrium chemistry (Leggett et al. Reference Leggett, Morley, Marley, Saumon, Fortney and Visscher2013).

3.3.1 Direct spectroscopy of resolved planets

A number of ‘planets’ have been discovered through direct imaging of young objects using ground-based adaptive optics or the Hubble Space Telescope. These include the companion of the brown dwarf 2MASSW J1207 334 − 393 254 (usually referred to as 2M 1207b — Chauvin et al. Reference Chauvin, Lagrange, Dumas, Zuckerman, Mouillet, Song, Beuzit and Lawrence2005), and the four planets of HR 8799 (Marois et al. Reference Marois, Macintosh, Barman, Zuckerman, Song, Patience, Lafreniere and Doyon2008, Reference Marois, Zuckerman, Konopacky, Macintosh and Barman2010).

The classification of some of these objects as planets is controversial. Although 2M 1207b was announced as the first directly imaged extrasolar planet by its discoverers, it can be argued that it is not a planet because it orbits a brown dwarf, not a star, or because it is unlikely that it formed through the normally understood planet formation process from a disk around its primary object (Soter Reference Soter2006). 2M 1207b is usually referred to as a ‘planetary mass object’ in recent literature.

The classification of such objects as planets also depends on the masses determined by application of evolutionary models, and this critically depends on the age. Marois et al. (Reference Marois, Zuckerman, Konopacky, Macintosh and Barman2010) use age ranges from 20 – 160 Myr for HR8799 to derive masses for the planets in the range 5 – 13 M _Jup placing them most likely below the deuterium burning limit. However, an age as high as ~ 1 Gyr is suggested by asteroseismology methods (Moya et al. Reference Moya, Amado, Barrado, Hernández, Aberasturi, Montesinos and Aceituno2010) which would make the objects brown dwarfs rather than planets. A number of recent studies based on dynamics (Moro-Martín, Rieke, & Su Reference Moro-Martín, Reike and Su2010; Sudol & Haghighipour Reference Sudol and Haghighipour2012) and a direct radius determination for HR 8799 (Baines et al. Reference Baines2012) favour a young age and planetary masses for the companions.

Near-IR spectra have been obtained for 2M 1207b (Mohanty et al. Reference Mohanty, Jayawardhana, Huélamo and Mamajek2007; Patience et al. Reference Patience, King, de Rosa and Marois2010), the HR 8799 planets (Bowler et al. Reference Bowler, Liu, Dupuy and Cushing2010; Barman et al. Reference Barman, Macintosh, Konopacky and Marois2011a; Oppenheimer et al. Reference Oppenheimer2013; Konopacky et al. Reference Konopacky, Barman, Macintosh and Marois2013) and β Pic b (Chilcote et al. Reference Chilcote2014). Spectra of 2M 1207b and HR 8799 b and c are shown in Figure 10. The spectra show the CO bandhead at 2.3 μm, and H₂O absorption at 1.4 and 1.9 μm (deepest in HR 8799b). CH₄ absorption is either absent or possibly weakly present in HR 8799b. The spectral features are similar to those of mid to late L dwarfs, which would imply objects of T_eff ~ 1400–1600 K.

Figure 10. Spectra of the direct imaged planets (or planetary mass objects) 2M 1207b (Patience et al. Reference Patience, King, de Rosa and Marois2010), HR 8799b (Barman et al. Reference Barman, Macintosh, Konopacky and Marois2011a) and HR 8799c (Konopacky et al. Reference Konopacky, Barman, Macintosh and Marois2013). The CO bandhead at 2.3 μm is apparent in all three objects as well as H₂O absorption at ~ 1.9 and ~ 1.4 μm.

However, photometry of 2M 1207b shows it to be very red in J − K and underluminous compared with L dwarfs (Figure 11). This led Mohanty et al. (Reference Mohanty, Jayawardhana, Huélamo and Mamajek2007) to suggest that grey extinction by an edge-on disk may be the cause of the underluminosity. Photometry of HR 8799b show that it is similarly underluminous. Barman et al. (Reference Barman, Macintosh, Konopacky and Marois2011b) have shown that it is possible to model the spectrum of 2M 1207b with a cool (T_eff ~ 1 000 K) model by including clouds and a departure from chemical equilibrium due to vertical mixing that inhibits the formation of methane. Similar models have been fitted to the spectra of HR 8799b (Barman et al. Reference Barman, Macintosh, Konopacky and Marois2011a) and c (Konopacky et al. Reference Konopacky, Barman, Macintosh and Marois2013).

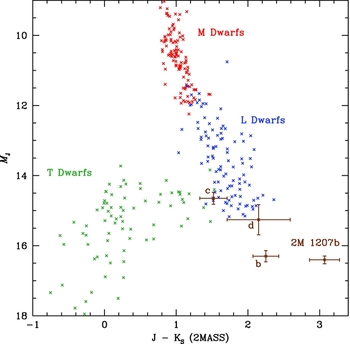
Figure 11. Colour magnitude diagram for 2M 1207b and the b, c and d planets of HR 8799 (photometry from Chauvin et al. Reference Chauvin, Lagrange, Dumas, Zuckerman, Mouillet, Song, Beuzit and Lawrence2005; Marois et al. Reference Marois, Macintosh, Barman, Zuckerman, Song, Patience, Lafreniere and Doyon2008; Mohanty et al. Reference Mohanty, Jayawardhana, Huélamo and Mamajek2007) compared with field M, L and T dwarfs (from the same data sources as Figure 5).

Spectroscopy of β Pic b in the H band (Chilcote et al. Reference Chilcote2014) taken with the Gemini Planet Imager shows spectral structure indicating H₂O absorption and atmospheric model fits give T_eff = 1 650 ± 50 K and log g = 4.0 ± 0.25.

A detection of methane (Janson et al. Reference Janson2013) has been reported in the planetary mass companion GJ 504b (Kuzuhara Reference Kuzuhara2013). This was achieved using Spectral Differential Imaging with the HiCAIO adaptive optics camera on the Subaru telescope. The companion was found to be much fainter in the CH₄ absorption band at ~ 1.7 μm than in other bands indicating a deep methane absorption comparable to that in late T dwarfs.

3.3.2 High resolution cross correlation techniques

Spectral features due to an unresolved extrasolar planet can be detected using high-resolution spectroscopy, and cross correlation techniques to pick out the faint signal due to the planet from the much brighter contribution of the host star. The technique was first used to attempt to detect the reflected light signal in high-resolution optical spectra of hot Jupiters. A possible detection of a planetary signal in τ Boo was reported (Collier Cameron et al. Reference Cameron, Horne, Penny and James1999) but was not confirmed (Charbonneau et al. Reference Charbonneau, Noyes, Korzennik, Nisenson, Jha, Vogt and Kilbrick1999; Leigh et al. Reference Leigh, Cameron, Horne, Penny and James2003a) and is inconsistent with the subsequent infrared detections by Brogi et al. (Reference Brogi, Snellen, de Kok, Albrecht, Birkby and de Mooij2012) and Rodler, Lopez-Morales, & Ribas (Reference Rodler, Lopez-Morales and Ribas2012). These studies set upper limits on the geometric albedo of τ Boo b of 0.3 at 480 nm (Charbonneau et al. Reference Charbonneau, Noyes, Korzennik, Nisenson, Jha, Vogt and Kilbrick1999) and 0.39 over 400–650 nm (Leigh et al. Reference Leigh, Cameron, Horne, Penny and James2003a). Other reflected light studies for a number of the brighter hot Jupiter systems (Collier Cameron et al. Reference Collier Cameron, Horne, Penny and Leigh2002; Leigh et al. Reference Leigh, Cameron, Udry, Donati, Horne, James and Penny2003b; Rodler, Kurster, & Henning Reference Rodler, Kurster and Henning2008, Reference Rodler, Kurster and Henning2010; Langford et al. Reference Langford, Wyithe, Turner, Jenkins, Narita, Liu, Suto and Toru2011) result in similar upper limits on geometric albedo.

Much more successful have been similar studies in the near-IR where it is possible to search for specific molecular absorption features either in the transmission spectrum during transit (Snellen et al. Reference Snellen, de Kok, de Mooij and Albrecht2010a) or in the thermal emission from the planet (which does not require a transiting planet). In these studies the telluric and stellar absorption features are removed as best as possible and the remaining signal is cross correlated with a template spectrum. The large radial velocity amplitude of the planet causes the absorption features to shift with orbital phase, so that a cross correlation peak can be searched for as a function of radial velocity amplitude (K _P ) and systemic velocity (V_sys ) as shown in Figure 12 (Brogi et al. Reference Brogi, Snellen, de Kok, Albrecht, Birkby and de Mooij2012).

Figure 12. Carbon monoxide cross correlation signal for τ Boo b (Brogi et al. Reference Brogi, Snellen, de Kok, Albrecht, Birkby and de Mooij2012) as a function of systemic velocity (V_sys ) and radial velocity amplitude of the planet (K_P ). A 6.2σ signal is seen at K_P = 110 ± 3.2 km s⁻¹ corresponding to an inclination i = 44.5° ± 1.5 and a planet mass M_P = 5.95 ± 0.28M_Jup — Reprinted by permission from Macmillan Publishers Ltd: Nature, 486, 502–504, © (2012).

The method determines K _P and thus provides a direct measurement of the planet’s mass and the orbital inclination, removing the sin i uncertainty for non-transiting planets. If the planet is transiting the results can be checked against those determined from transit analysis. The systemic velocity is also determined and should agree with that measured for the host star. Table 2 list the detections reported. For two objects (τ Boo b and HD 189733b) there are independent results from two studies that are in good agreement.

Table 2. High-Resolution Cross Correlation Detections

^a Transmission spectrum during transit. All others are dayside emission detections.

Most of the objects observed in this way are hot Jupiters, but essentially the same method has also been applied to the directly imaged exoplanet β Pic b (Snellen et al. Reference Snellen, Brandl, de Kok, Brogi, Birkby and Schwarz2014). In this case it was possible to detect rotational broadening of about 25 kms⁻¹ in the CO cross correlation signal indicating a rapid rotation for the planet.

All detections so far are either for carbon monoxide or water. In HD189733b (de Kok et al. Reference de Kok, Brogi, Snellen, Birkby, Albrecht and de Mooij2013) CO₂, CH₄ and H₂O were searched for in the 2 μm region but not detected. However, H₂O was detected in HD 189733b using longer wavelength (3.2 μm) observations (Birkby et al. Reference Birkby, de Kok, Brogi, de Mooij, Schwarz, Albrecht and Snellen2013). While CO is expected to be strong feature in these planets, part of the reason it is most easily detected may be that as a diatomic molecule it has a simpler spectrum and better quality line lists. Difficulty in detecting other species may, in part, be due to errors in the template spectra due to problems with the line lists, such as errors in line positions (see discussion in Barnes et al. Reference Barnes2010) and incompleteness. Methane line lists used for atmospheric modelling are known to be missing many hot bands that are needed at the high temperatures of these objects.

3.3.3 Secondary eclipse photometry and spectroscopy

The secondary eclipse (or occultationFootnote ² ) occurs when a planet passes behind the star. If the planet is sufficiently bright a measurable dip in the light curve is seen, and the fractional depth of the dip is a direct measurement of the flux from the planet as a fraction of that from the star. In most cases such measurements detect thermal emission from the dayside of the planet, and so contrasts are greatest at infrared wavelengths.

The first detection of a secondary eclipse was made at 24 μm for HD 209458b using the Spitzer Space Telescope (Deming et al. Reference Deming, Seager, Richardson and Harrington2005). Since then a substantial number of mostly hot Jupiter type systems have had their secondary eclipse depth measured in the Spitzer/IRAC bands (3.6 μm, 4.5 μm, 5.8 μm and 8.0 μm). There are also a number of measurements at shorter wavelengths from ground-based telescopes. The broad band eclipse depth results are summarised in Table 3. This lists secondary eclipse depths measured in the four Spitzer/IRAC bands and in the K _s band (2.15 μm). Where there are multiple measurements in a band the one with the smaller quoted error is listed, but references to all measurements are given. The ‘Other’ column lists other bands in which eclipse depths have been measured and the references to these are also given.

Table 3. Secondary eclipse depth broadband measurements (%)

^a Value from Croll et al. (Reference Croll, Lafreniere, Loic, Jayawardhana, Fortney and Murray2011) as corrected by Crossfield et al. (Reference Crossfield, Barman, Hansen, Ichi and Kodama2012b)

^b Values from Campo et al. (Reference Campo2011) as corrected by Crossfield et al. (Reference Crossfield, Barman, Hansen, Ichi and Kodama2012b)

References 1. Deming et al. (Reference Deming2011), 2. Gillon et al. (Reference Gillon2009), 3. Rogers et al. (Reference Rogers, Apai, López-Morales, Sing and Burrows2009), 4. Snellen et al. (Reference Snellen, de Mooij and Albrecht2009), 5. Deming et al. (Reference Deming2011), 6. Gillon et al. (Reference Gillon2010), 7. Snellen et al. (Reference Snellen, de Mooij and Burrows2010b), 8. Deming et al. (Reference Deming, Harrington, Laughlin, Seager, Navarro, Bowman and Horning2007), 9. Stevenson et al. (Reference Stevenson2012), 10. Charbonneau et al. (Reference Charbonneau, Knutson, Barman, Allen, Mayor, Megeath, Queloz and Udry2008), 11. Knutson et al. (Reference Knutson2012), 12. Deming et al. (Reference Deming, Harrington, Seager and Richardson2006), 13. Deming et al. (Reference Deming, Seager, Richardson and Harrington2005), 14. Knutson et al. (Reference Knutson, Charbonneau, Allen, Burrows and Megeath2008), 15. Crossfield et al. (Reference Crossfield, Knutson, Fortney, Showman, Cowan and Deming2012a), 16. Todorov et al. (Reference Todorov, Deming, Harrington, Stevenson, Bowman, Nymeyer, Fortney and Bakos2010), 17. de Mooij et al. (Reference de Mooij, de Kok, Nefs and Snellen2011), 18. Todorov et al. (Reference Todorov2013), 19. Todorov et al. (Reference Todorov2012), 20 Christiansen et al. (Reference Christiansen2010), 21. Désert et al. (Reference Désert2011a), 22. Fortney et al. (Reference Fortney2011), 23. Charbonneau et al. (Reference Charbonneau2005), 24. O’Donovan et al. (Reference O’Donovan, Charbonneau, Harrington, Madhusudhan, Seager, Deming and Knutson2010), 25. Croll et al. (Reference Croll, Jayawardhana, Fortney, Lafrenière and Loic2010a), 26. Fressin et al. (Reference Fressin, Knutson, Charbonneau, O’Donovan, Burrows, Deming, Mandushev and Spiegel2010), 27. de Mooij & Snellen (Reference de Mooij and Snellen2009), 28. Croll et al. (Reference Croll, Loic, Lafreniere, Jayawardhanan and Fortney2010b), 29. Knutson et al. (Reference Knutson, Charbonneau, Burrows, O’Donovan and Mandushev2009a), 30. Zhao et al. (Reference Zhao, Monnier, Swain, Barman and Hinkley2012a), 31. Beerer et al. (Reference Beerer2011), 32. Cáceres et al. (Reference Cáceres2011), 33. Baskin et al. (Reference Baskin2013), 34. Cubillas et al. (Reference Cubillas2013), 35. Campo et al. (Reference Campo2011), 36. Croll et al. (Reference Croll, Lafreniere, Loic, Jayawardhana, Fortney and Murray2011), 37. Crossfield et al. (Reference Crossfield, Barman, Hansen, Ichi and Kodama2012b), 38. Zhao et al. (Reference Zhao, Milburn, Barman, Hinkley, Swain, Wright and Monnier2012b), 39. Cowan et al. (Reference Cowan, Machalek, Croll, Shekhtman, Burrows, Deming, Greene and Hora2012b), 40. López-Morales et al. (Reference López-Morales, Coughlin, Sing, Burrows, Apai, Rogers, Spiegel and Adams2010), 41. Anderson et al. (Reference Anderson2011), 42. Nyemeyer et al. (Reference Nyemeyer2011), 43. Maxted et al. (Reference Maxted2013), 44. Anderson et al. (Reference Anderson2013), 45. Gibson et al. (Reference Gibson2010), 46. Lendl et al. (Reference Lendl, Gillon, Queloz, Alonso, Fumel, Jehin and Naef2013), 47. Burton et al. (Reference Burton, Watson, Littlefair, Dhillon, Gibson, Marsh and Pollacco2012), 48. Smith et al. (Reference Smith2012), 49. Mahtani et al. (Reference Mahtani2013), 50. Deming et al. (Reference Deming2012), 51. de Mooij et al. (Reference de Mooij, Brogi, de Kok, Snellen, Kenworthy and Karjaleinen2013), 52. Smith et al. (Reference Smith, Anderson, Skillen, Collier-Cameron and Smalley2011), 53. Blecic et al. (Reference Blecic2014), 54. Machalek et al. (Reference Machalek, McCullough, Burke, Valenti, Burrows and Hora2008), 55. Machalek et al. (Reference Machalek, McCullough, Burrows, Burke, Hora and Johns-Crull2009), 56. Machalek et al. (Reference Machalek, Greene, McCullough, Burrows, Burke, Hora, Johns-Krull and Deming2010), 57. Zhou et al. (Reference Zhou, Kedziora-Chuczer, Bayliss and Bailey2013), 58. Stevenson et al. (Reference Stevenson2010), 59. Agol et al. (Reference Agol, Cowan, Knutson, Deming, Steffen, Henry and Charbonneau2010), 60. O’Rourke et al. (Reference O’Rourke2014), 61. Blecic et al. (Reference Blecic2013), 62. Zellem et al. (Reference Zellem2014), 63. Chen et al. (Reference Chen, van Boekel, Madhusudhan, Wang, Nikolov, Seeman and Henning2014a), 64. Rostron et al. (Reference Rostron2014), 65. Chen et al. (Reference Chen, van Boekel, Wang, Nikolov, Seemann and Henning2014b), 66. Wang et al. (Reference Wang, van Boekel, Madhusudhan, Chen, Zhao and Henning2013), 67. Zhou et al. (Reference Zhou, Bayliss, Kedziora-Chudczer, Salter, Tinney and Bailey2014)

For a few of the brighter systems it is possible to go further and obtain spectra of the dayside emission using the secondary eclipse depth. Such results are listed in Table 4. Figure 13 shows the combined data from broad band and spectroscopic observations for some of the best studied cases.

Figure 13. Dayside emission from WASP-12b, WASP-19b, HD189733b and HD209458b based on data listed in Tables 3 and 4. Large symbols are broad band measurements and smaller symbols are spectroscopic observations.

Table 4. Dayside emission spectroscopy from secondary eclipses.

With secondary eclipse data of sufficient quality it is possible to map the brightness distribution across the disk of the planet (Williams et al. Reference Williams, Charbonneau, Cooper, Showman and Fortney2006). This has been attempted for HD 189733b by Majeau, Agol, & Cowan (Reference Majeau, Agol and Cowan2012) and de Wit et al. (Reference de Wit, Gillon, Demory and Seager2012). The results show a bright spot shifted east from the subsolar point in agreement with results from the full phase light curve (Knutson et al. Reference Knutson2007a)

While the infrared secondary eclipse shows the thermal emission from the planet, observations of the secondary eclipse at visible wavelengths can show the planet through light reflected from its star. However, if the planet is very hot, thermal emission may still be present even at visible wavelengths. Table 5 summarises measurements so far, mostly from observations with Kepler, in a broad band covering 400–850 nm. These observations provide a measure of the geometric albedo of the planet, and show that some of these planets are quite dark, while others have geometric albedos up to ~ 0.4. In the case of HD 189733b observations have been made with STIS showing the planet to be dark at 450–570 nm, but with an albedo of 0.4 at 290–450 nm, the blue colour being indicative of a Rayleigh scattering haze (Evans et al. Reference Evans2013). Low albedos in the visible are to be expected for clear atmospheres due to the broad sodium and absorption lines, whereas higher albedos can result if clouds are present (Sudarsky, Burrows, & Pinto Reference Sudarsky, Burrows and Pinto2000).

Table 5. Geometric albedo measurements from optical secondary eclipses.

All measurements are with Kepler (400–850 nm) except for HD 209458b observed with MOST (350–700 nm) and HD 189733b observed with HST/STIS.

3.3.4 Transit spectroscopy

Observations during transit (or primary eclipse, when the planet passes in front of the star) also provide information on the atmospheres. The depth of the primary eclipse is a measure of the radius of the planet, and will be larger where absorption is strongest.

Spectroscopy during transits can reveal absorption features in the transmission spectrum of the planet’s atmosphere. Transit spectroscopy samples the terminator of the planet and the long tangent path length means that it is sensitive to higher levels in the atmosphere than dayside emission spectroscopy from secondary eclipses.

The first detection of an exoplanet atmosphere was in observations of the transits of HD 209458 (Charbonneau et al. Reference Charbonneau, Brown, Noyes and Gilliland2002) that showed absorption in the sodium doublet at 589.3 nm. Transit spectroscopy (other than studies of Na line absorption) studies are listed in Table 6. In addition to these spectroscopy observations there are numerous transit measurements in broad band filters, including measurements in the Spitzer/IRAC bands that extend coverage to longer wavelengths. HD 189733b is a particularly well studied system, and the various space observations have been combined by Pont et al. (Reference Pont, Sing, Gibson, Aigrain, Henry and Husnoo2013) to give the transmission spectrum shown in Figure 14. It shows increasing absorption to the blue indicating the presence of a Rayleigh scattering haze. Wasp 12b (Sing et al. Reference Sing2013) also shows a similar increase to the blue attributed to Rayleigh scattering from aerosols.

Figure 14. Transmission spectrum of HD 189733b from HST and Spitzer transit observations, showing increase to the blue interpreted as due to a Rayleigh scattering haze. — Figure 9 from ‘The prevalence of dust on the exoplanet HD189733b from Hubble and Spitzer observations’, Pont, F. et al., 2013, MNRAS, 432, 2917.

Table 6. Transmission spectroscopy during transit.

^a According to reanalysis by Barman (Reference Barman2007).

Transmission spectra in the near-IR for three systems are shown in Figure 15, showing water vapour absorption at ~ 1.4 μm. As is conventional, these observations are plotted as R _P /R _S (i.e. the radius of the planet divided by the radius of the star as determined from the transit). This gives an inverted spectrum compared with conventional spectroscopy, since absorption features increase the apparent radius of the planet.

Figure 15. HST/WFC3 observations of the transmission spectra of HD209458b and XO-1b (Deming et al. Reference Deming2013) and HAT-P-1b (Wakeford et al. Reference Wakeford2013) showing absorption at ~ 1.4 μm attributed to H₂O. The spectrum of the brown dwarf Kelu-1 showing the same absorption feature is shown for comparison in the bottom panel. The exoplanet spectra are inverted compared with the brown dwarf spectra since absorption features increase the radius of the planet as seen in transit observations.

Measurements of the Sodium D-line absorption are listed in Table 7. Results are listed here where the absorption is detected at greater than the 3-sigma level. There are also a number of unsuccesful attempts at detections. Potassium absorption has been reported in XO-2b (Sing et al. Reference Sing2011b).

Table 7. Sodium (589 nm) detections from transit spectroscopy.

^a 7.0 ± 1.1 × 10⁻⁴ (0.15 nm band), 13.5 ± 1.7 × 10⁻⁴ (0.075 nm band)

Atomic and atomic ion species have also been detected in a number of transiting planets in the unbound portion of the atmosphere, or exosphere. The best studied case is HD 209458b where H I, C II, O I, and Si III have been observed (Vidal-Madjar et al. Reference Vidal-Madjar, Lecavelier des Etangs, Désert, Ballester, Ferlet, Hébrard and Mayor2003, Reference Vidal-Madjar2004; Linsky et al. Reference Linsky, Yang, France, Froning, Green, Stocke and Osterman2010). Exosphere detections have also been reported in HD 189733b (Lecavelier Des Etangs et al. Reference Lecavelier des Etangs2010; Jensen et al. Reference Jensen, Redfield, Endl, Cochran, Koesterke and Barman2012) and Wasp-12b (Fossati et al. Reference Fossati2010).

3.3.5 Full phase photometry

As well as observations of the transits and eclipses, information on a planet’s atmosphere can be obtained from observations of the full phase light curve. In the infrared a hot Jupiter will show variations around the cycle due to the variation of temperature across its surface. In the optical where reflected light is seen, variations will occur due to the change in the illuminated fraction of the disk, as well as due to phase angle dependent scattering processes (Seager, Whitney, & Sasselov Reference Seager, Whitney and Sasselov2000). In some cases the light curves are complicated by ellipsoidal variations in the star (e.g. Welsh et al. Reference Welsh2010) or the planet (e.g. Cowan et al. Reference Cowan, Machalek, Croll, Shekhtman, Burrows, Deming, Greene and Hora2012b). Systems with full phase light curves at infrared wavelengths showing significant variation around the cycle are listed in Table 8. In addition full phase light curves due to reflected light are observed in many of the systems listed in Table 5.

Table 8. Full phase infrared photometry of exoplanets.

Analysis of these light curves has been used to derive maps of the temperature distribution of HD 189733b (Knutson et al. Reference Knutson2007a) showing a hot spot offset from the substellar point (consistent with models, see Section 4.1.3). In the case of Kepler-7b, the reflected light phase curve observed by Kepler is interpreted as showing the presence of patchy clouds (Demory et al. Reference Demory2013).

3.3.6 Polarimetry

Reflected light from extrasolar planets will be polarised as a result of scattering from cloud and haze particles and from molecules. Normal stars are generally found to have very low intrinsic polarisations (Kemp et al. Reference Kemp, Henson, Steiner and Powell1987; Bailey, Lucas, & Hough Reference Bailey, Lucas and Hough2010). In a hot Jupiter system the polarisation in the combined light of the unresolved star and planet is expected to be in the range 10⁻⁵–10⁻⁶ (Seager, Whitney, & Sasselov Reference Seager, Whitney and Sasselov2000), and will vary around the orbital cycle with the changing phase angle.

While the expected polarisations are small, polarisation is a differential measurement that can be made to high sensitivity wth ground-based telescopes, and instruments capable of measuring stellar polarisation at the one part per million level have been developed (Hough et al. Reference Hough, Lucas, Bailey, Tamura, Hirst, Harrison and Bartholomew-Biggs2006; Wiktorowicz & Matthews Reference Wiktorowicz and Matthews2008). Lucas et al. (Reference Lucas, Hough, Bailey, Tamura, Hirst and Harrison2009) reported upper limits on the polarisation of τ Boo and 55 Cnc in a broad red band (590–920 nm) and set upper limits on the geometric albedo of τ Boo b and 55 Cnc e for Rayleigh scattering models.

Berdyugina et al. (Reference Berdyugina, Berdyugin, Fluri and Piirola2008) reported polarisation varying over the orbital cycle of HD 189733b with an amplitude of ~ 2 × 10⁻⁴ in the B band. Wiktorowicz (Reference Wiktorowicz2009), however, found no polarisation variation in this system with a 99% confidence upper limit of 7.9 × 10⁻⁵ in a 400–675 nm wavelength range. Berdyugina et al. (Reference Berdyugina, Berdyugin, Fluri and Piirola2011) then reported further observations that confirmed a polarisation variation, but with a reduced amplitude of 10⁻⁴ in the U and B bands and much lower amplitude in the V band. They claim the data is consistent with that of Wiktorowicz (Reference Wiktorowicz2009) when the different wavelengths are taken into account.

While HD 189733b is a system in which polarisation might be expected in view of the Rayleigh scattering haze seen in transmission spectroscopy (Pont et al. Reference Pont, Knutson, Gilliland, Moutou and Charbonneau2008, Reference Pont, Sing, Gibson, Aigrain, Henry and Husnoo2013), the reported polarisation amplitudes are too large to be easily explained. Berdyugina et al. (Reference Berdyugina, Berdyugin, Fluri and Piirola2011) report that the polarisation is consistent with a Rayleigh-Lambert model with a geometric albedo of ~ 0.6 and ‘scattered light maximally polarised’ (i.e. 100%). However, in Rayleigh scattering models a layer sufficiently optically thick to produce a high geometric albedo has a maximum polarisation of only about 30% (Buenzli & Schmid Reference Buenzli and Schmid2009) as a result of depolarisation due to multiple scattering. Lucas et al. (Reference Lucas, Hough, Bailey, Tamura, Hirst and Harrison2009) used Monte-Carlo scattering models to predict a maximum polarisation amplitude of 2.6 × 10⁻⁵ for HD 189733b.

3.4.1 Inflated atmospheres

One result of transit observations is that many hot Jupiters are ‘inflated’, with radii significantly larger than predicted by models (Baraffe, Chabrier, & Barman Reference Baraffe, Chabrier and Barman2008, Reference Baraffe, Chabrier and Barman2010). This inflation is found to be correlated with the level of stellar irradiation, with inflation becoming apparent for planets receiving incident flux greater than 2 × 10⁸ erg s⁻¹ cm⁻² (Miller & Fortney Reference Miller and Fortney2011; Demory & Seager Reference Demory and Seager2011).

Weiss et al. (Reference Weiss2013) have used data on 138 exoplanets to derive empirical relations between radius, mass and incident flux as follows:

(1) \begin{equation} R_P/R_{\hbox{$\oplus $}} = 1.78 (M_P/M_{\hbox{$\oplus $}})^{0.53} (F/\mbox{erg s$^{-1}$ cm$^{-2}$})^{-0.03} \end{equation}

for M_P < 150M _⊕, and

(2) \begin{equation} R_P/R_{\hbox{$\oplus $}} = 2.45 (M_P/M_{\hbox{$\oplus $}})^{-0.039} (F/\mbox{erg s$^{-1}$ cm$^{-2}$})^{0.094} \end{equation}

for M_P > 150M _⊕.

The reason for this inflation is still debated. Guillot & Showman (Reference Guillot and Showman2002) showed that the inflated radii could be understood if ~ 1% of the stellar flux received by the planet was transferred into the deep atmosphere below the photosphere. The observed relationships between inflated radii and incident flux appear consistent with this idea. However, it is unclear what is the mechanism for transferring energy into the interior. Mechanisms for inflated radii include downward transport of mechanical energy by atmospheric circulation (Showman & Guillot Reference Showman and Guillot2002), enhanced opacities that help to trap heat in the interior (Burrows et al. Reference Burrows, Hubeny, Budaj and Hubbard2007a), dissipation of thermal tides (Arras & Socrates Reference Arras and Socrates2010), and tidal heating due to a non-zero eccentricity (Jackson et al. Reference Jackson, Greenberg and Barnes2008; Ibgui, Burrows, & Spiegel Reference Ibgui, Burrows and Spiegel2010). The Ohmic dissipation model (Batygin & Stevenson Reference Batygin and Stevenson2010; Perna, Menou, & Rauscher Reference Perna, Menou and Rauscher2010) uses the interaction of atmospheric winds and the planetary magnetic field to induce electric currents that heats the interior. Rauscher & Menou (Reference Rauscher and Menou2013) have modelled the process using a 3D model (see Section 4.1.3) and find that ohmic dissipation can explain the radius of HD 209458b for a planetary magnetic field of 3–10 G. However, Rogers & Showman (Reference Rogers and Showman2014) used 3D magnetohydrodynamic simulations of the atmosphere of HD 209458b and found Ohmic dissipation rates orders of magntiude too small to explain the inflated radius.

3.4.2 Temperature structure

The dayside spectra of hot Jupiters as defined by the Spitzer IRAC colours (Table 3 and Figure 13) have been used to derive information on the atmospheric temperature structure. If temperature decreases with height then the spectrum shows absorption features due to its atmospheric molecules, but a temperature inversion can cause the same features to appear in emission. A constant temperature (isothermal) atmosphere would shown no spectral features.

The presence of a temperature inversion was first suggested in the infrared spectrum of HD 209458b (Knutson et al. Reference Knutson, Charbonneau, Allen, Burrows and Megeath2008; Burrows et al. Reference Burrows, Hubeny, Budaj and Hubbard2007a) where a bump in the spectrum at 4.5 and 5.8 μm can be understood as water vapour in emission. A number of other cases have been suggested based on Spitzer photometry. It has been suggested that inversions result from absorption of starlight by an absorber high in the atmosphere. Suggestions for the absorber include TiO and VO (Hubeny et al. Reference Hubeny, Burrows and Sudarsky2003; Fortney et al. Reference Fortney, Lodders, Marley and Freedman2008) or photochemically produced sulfur compounds (Zahnle et al. Reference Zahnle, Marley, Freedman, Lodders and Fortney2009). However, observations have so far failed to detect the presence of TiO or VO in eclipse or transit spectroscopy in any of these systems.

Knutson, Howard, & Isaccson (Reference Knutson, Howard and Isaacson2010) argue that the presence of an inversion correlates with the activity of the host star, with the temperature inversions being found for planets orbiting inactive stars, whereas the non-inverted atmospheres occur in planets orbiting chromospherically active stars.

However, Madhusudhan & Seager (Reference Madhusudhan and Seager2010) have investigated the degeneracies between thermal inversions and molecular abudnances, and find it is often possible to fit both inversion and non-inversion models given the limited data points available from Spitzer photometry.

3.5.1 Water vapour, carbon monoxide and methane

Analogy with brown dwarfs of similar temperatures discussed in Section 2 suggests that the most important species in the near-IR spectra should be H₂O, CO and CH₄. From the discussion in Section 3.3 and Tables 2–6, it will be apparent that H₂O and CO are indeed detected in quite a number of giant exoplanet systems by a variety of different methods. Evidence for these molecules is found in spectroscopy of direct imaged planets (Section 3.3.1), from high resolution cross correlation methods (Section 3.3.2 and Table 2) and from secondary eclipse (Section 3.3.3, Table 4) and transit (Section 3.3.4 and Table 6) spectroscopy.

The data on CH₄ is less clear. Although it is reported, for example, in the NICMOS transmission spectrum of HD 189733b (Swain et al. Reference Swain, Vasisht and Tinetti2008), high resolution cross correlation studies at the same wavelength do not detect it (de Kok et al. Reference de Kok, Brogi, Snellen, Birkby, Albrecht and de Mooij2013), but do detect CO. This suggests a departure from equilibrium chemistry due to vertical mixing as also suggested by Knutson et al. (Reference Knutson2012) based on Spitzer phase curves.

The spectra of directly imaged planets shown in Figure 10 also show CO, but at best very weak evidence for CH₄. These are all objects that are cool enough to be in the T dwarf range, but actually show spectra more like those of L dwarfs. The lack of CH₄ once again indicates non-equilibrium chemistry (Barman et al. Reference Barman, Macintosh, Konopacky and Marois2011a, Reference Barman, Macintosh, Konopacky and Marois2011b; Skemer et al. Reference Skemer2014; Zahnle & Marley Reference Zahnle and Marley2014). Departures from equilibrium chemistry are discussed further in Section 4.2.2.

Recently, however, CH₄ has been detected photometrically in the very cool ( ~ 600 K) planetary mass companion GJ 504b (Janson et al. Reference Janson2013) as described in Section 3.3.1

3.5.2 Carbon dioxide

Up to a few years ago CO₂ was not considered to be an important species for exoplanet and brown dwarf atmospheres as its predicted equilibrium abundance is quite low. Then Swain et al. (Reference Swain, Vasischt, Tinetti, Bouwman, Chen, Yung, Deming and Deroo2009a) reported an absorption feature at 2.0 μm in the NICMOS dayside emission spectrum of HD189733b that they identified as CO₂. This is a relatively weak CO₂ band. It has never been seen in brown dwarfs, for example, whereas the much stronger CO₂ band at 4.2 μm has been seen (Yamamura, Tsuji, & Tanabé Reference Yamamura, Tsuji and Tanabé2010; Sorahana & Yamamura Reference Sorahana and Yamamura2012).

Fitting the NICMOS feature at 2.0 μm in HD189733b as a CO₂ band results in CO₂ mole fractions ~ 10⁻³ (Madhusudhan & Seager Reference Madhusudhan and Seager2009; Lee, Fletcher, & Irwin Reference Lee, Fletcher and Irwin2012; Line et al. Reference Line, Zhang, Vasischt, Natraj, Chen and Yung2012). This is several thousand times higher than the expected chemical equilibrium abundance for solar composition (Moses et al. Reference Moses2011) or the observed CO₂ abundances in brown dwarfs (Tsuji, Yamamura, & Sorahana Reference Tsuji, Yamamura and Sorahana2011). Inclusion of non-equilibrium processes such as photochemistry does not substantially increase CO₂ abundances (Zahnle et al. Reference Zahnle, Marley, Freedman, Lodders and Fortney2009; Moses et al. Reference Moses2011). However, CO₂ abundances are sensitive to elemental composition increasing quadratically with increasing metallicity (Lodders Reference Lodders2002; Zahnle et al. Reference Zahnle, Marley, Freedman, Lodders and Fortney2009).

The high CO₂ abundance is not clearly seen in other observations of HD189733b. In particular the much stronger CO₂ bands at 4.2 μm and 15 μm are not apparent in the Spitzer secondary eclipse data. Fitting separately to the NICMOS and Spitzer data, Madhusudhan & Seager (Reference Madhusudhan and Seager2009) found a much lower CO₂ abundance from the Spitzer data consistent with equilibrium predictions. If a model is required to fit both the Spitzer and NICMOS data simultaneously, as in the retrieval analysis of Lee et al. (Reference Lee, Fletcher and Irwin2012) the result is a very high CO₂ abundance to fit the NICMOS data, and then a tightly constrained isothermal temperature profile in the upper atmosphere, which hides the strong 4.2 μm and 15 μm CO₂ bands that would otherwise be present.

An alternative interpreation is to disregard the NICMOS 2 μm feature, the only evidence pointing to a high CO₂ abundance in HD 189733b. Gibson et al. (Reference Gibson, Pont and Aigrain2011) have argued that NICMOS observations are too sensitive to the method of removing systematics to reliably detect molecular species. In that case it is possible to fit the remaining data on the transmission and dayside emission spectra of HD 189733b very well using equilibrium abundances as shown by Dobbs-Dixon & Agol (Reference Dobbs-Dixon and Agol2013) who used the solar composition opacities from Sharp & Burrows (Reference Sharp and Burrows2007).

3.5.3 C/O ratios

A high C/O ratio was first suggested for the atmosphere of the highly irradiated hot Jupiter WASP-12b (Madhusudhan et al. Reference Madhusudhan2011) and Madhusudhan (Reference Madhusudhan2012) has suggested that C/O ratio may be an important parameter for classifying exoplanet atmospheres. If C/O is greater than 1.0 (the solar value is about 0.5) the chemistry changes substantially for temperatures above about 1 500 K, since almost all the oxygen combines with carbon to form CO, and the abundances of other oxygen bearing species, including H₂O and TiO/VO are substantially reduced. The excess carbon also results in increased abundances of carbon species such as HCN and C₂H₂.

Reanalysis of the secondary eclipse data on WASP-12b by Crossfield et al. (Reference Crossfield, Barman, Hansen, Ichi and Kodama2012b), with corrections for the effects of a contaminating star, concluded that the spectrum was well-approximated by a blackbody and that no constraints on its atmospheric abundances could be set. Other recent studies of the emission and transmission spectra of WASP-12b (Sing et al. Reference Sing2013; Swain et al. Reference Swain2013; Mandell et al. Reference Mandell, Haynes, Sinukoff, Madhusudhan, Burrows and Deming2013) do not clearly detect any molecular species and do not significantly constrain the C/O ratio.

Line et al. (Reference Line2013b) have investigated the ability to determine C/O ratios using retrieval models (see Section 4.1.2) and find that with limited data this is very difficult and the retrieved values are biased towards the solar value or a value of one.

4.1.1 Stellar atmosphere type models

The traditional approach to stellar atmosphere modelling is typified by the ATLAS series of modelling codes (Kurucz Reference Kurucz1970, Reference Kurucz1993; Castelli & Kurucz Reference Castelli and Kurucz2004), and the MARCS models (Gustaffson et al. Reference Gustaffson, Edvardsson, Eriksson, Jørgensen, Nordlund and Plez2008). Normally with such models the starting point is an adopted effective temperature T _eff, surface gravity (usually specified as log g in cgs units), and metallicity [M/H]. Grids of models can then be calculated for different values of these parameters. The essential stages in such models are:

1. 1. Start with an initial estimate for the pressure temperature structure of the atmosphere specified at a number ( ~ 40–80) of layers.

2. 2. For each layer calculate the composition of the layer. For hotter stars this primarily involves determining the distribution of ionisation states for each element using Saha’s equation. For cooler stars some molecules become important and their concentrations are calculated assuming chemical equilibrium.

3. 3. Calculate the opacity (extinction coefficient) of each layer at each required wavelength taking account of atomic absorption lines, molecular absorption lines and continuum opacity sources such as bound-free and free-free absorption, collision induced absorptions, Rayleigh and electron scattering. The wavelength range must cover all wavelengths at which significant energy transport occurs.

4. 4. Solve the radiative transfer equation to determine the radiative energy flux through each layer.

5. 5. Iteratively adjust the temperature structure of the model, repeating steps 2–4 as required until the model is in energy balance. The total flux through each layer, including convective energy flux which is normally determined using mixing length theory (Henyey, Vardya, & Bodenheimer Reference Henyey, Vardya and Bodenheimer1965) must equal σT ⁴ _eff.

The spectrum of the star can then be obtained, either from the last iteration of the model if opacities and radiative transfer are calculated with sufficient resolution, or from a separate spectral synthesis model.

Models based on essentially this procedure have been developed for brown dwarf and exoplanet atmospheres (e.g. Tsuji et al. Reference Tsuji, Ohnaka, Aoki and Nakajima1996; Allard et al. Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001; Barman, Hauschildt, & Allard Reference Barman, Hauschildt and Allard2001; Marley et al. Reference Marley, Seager, Saumon, Lodders, Ackerman, Freedman and Fan2002; Burrows, Sudarsky, & Hubeny Reference Burrows, Sudarsky and Hubeny2003). In order to model the atmospheres of these cooler objects a number of additional complications have to be dealt with.

At lower temperatures the composition becomes dominated by molecules (as shown in Figure 3), and the calculation of composition (or equation of state) becomes primarily a chemical model. Large numbers of chemical compounds are potentially important and hence large chemical models handling hundreds or in some case thousands of species have been developed (e.g Lodders & Fegley Reference Lodders and Fegley2002). (see Section 4.2).

As well as gas phase species, at temperatures below about 2 000 K condensates start to form and both modify the gas phase chemistry, and can form clouds that contribute substantially to the opacity. As we have already seen clouds are important in understanding the behaviour of L dwarfs and the L/T transition, and are also probably important in giant exoplanets. (see Section 4.4).

Molecules and cloud particles contribute to scattering of light. Scattering is usually a relatively minor contribution to the opacity of stellar atmospheres and is usually treated using simplifying approximations such as that of isotropic scattering. In the cooler atmospheres of brown dwarfs and exoplanets scattering becomes more significant, and more rigorous treatments of scattering that accurately account for the non-isotropic phase functions may be needed (de Kok et al. Reference de Kok, Helling, Stam, Woitke and Witte2011; Bailey & Kedziora-Chudczer Reference Bailey and Kedziora-Chudczer2012). (see Section 4.5).

4.1.2 Retrieval models

A different approach to modelling exoplanet atmospheres is shown in a number of recent studies (Madhusudhan & Seager Reference Madhusudhan and Seager2009; Line et al. Reference Line, Zhang, Vasischt, Natraj, Chen and Yung2012; Lee et al. Reference Lee, Fletcher and Irwin2012; Benneke & Seager Reference Benneke and Seager2012; Line et al. Reference Line2013b; Benneke & Seager Reference Benneke and Seager2013) that adopt a retrieval approach. These approaches are similar to that used in remote sensing studies of the Earth atmosphere where temperature structure (e.g. Rozenkranz Reference Rosenkranz2001) trace gas content (e.g. Buchwitz et al. Reference Buchwitz2005), and cloud properties (e.g. Garnier et al. Reference Garnier, Pelon, Dubuisson, Chomette, Pascal and Kratz2012) are routinely retrieved from satellite observations, and similar techniques are used to study the atmospheres of other Solar system planets from orbiting spacecraft or Earth-based telescopes.

These models seek to retrieve the temperature structure and composition of the atmosphere directly from observations, rather than predict these using energy balance and chemical models as in the approach described above. Thus only steps 3 and 4 of the modelling procedure are needed in the forward model. A number of different approaches to the retrieval process have been used. Madhusudhan & Seager (Reference Madhusudhan and Seager2009) search in a large grid of models covering a wide parameter space. Lee et al. (Reference Lee, Fletcher and Irwin2012) use an iterative optimal estimation procedure. Line et al. (Reference Line2013b) investigate several different approaches to retrieval (Optimal Estimation, Bootstrap Monte Carlo, and Differential Evolution Markov Chain Monte Carlo).

Benneke & Seager (Reference Benneke and Seager2012, Reference Benneke and Seager2013) use a somewhat different approach where the temperature profile is not retrieved, but is determined by a self consistent model requiring radiative and hydrostatic equilibrium and allowing for convection. The model can therefore be described by a small number of parameters (planet-to-star radius ratio, cloud-top pressure and Bond albedo) as well as the mole fractions of molecular species. The models include cloud and haze layers and retrieval uses a Bayesian Nested Sampling Monte Carlo method.

4.1.3 3D models of hot Jupiters

All the models considered so far are 1D models that describe the structure of the atmosphere with a single one dimensional profile. Such models cannot represent dynamical effects and diurnal variations. For hot Jupiters which all receive strong irradiation from their star, the structure is expected to vary substantially around the planet and can be very different on the dayside and nightside.

A number of studies have looked at full 3D models of the atmospheric circulation (General Circulation Models or GCMs) for hot Jupiters. A GCM typically consists of a dynamical core (usually adpated from an Earth atmosphere model) that numerically solves the equations that govern atmospheric circulation over a three dimensional grid of points. These equations can either be the ‘primitive equations’ that include the approximations of vertical hydrostatic equilibrium and a shallow atmosphere as used by Showman et al. (Reference Showman, Fortney, Lian, Marley, Freedman, Knutson and Charbonneau2009) and Rauscher & Menou (Reference Rauscher and Menou2012) or the full equations that avoid these approximations as used by Dobbs-Dixon & Lin (Reference Dobbs-Dixon and Lin2008) and Mayne et al (Reference Mayne2014). Initially simplified schemes were used to represent the forcing from the illuminating star (e.g. Showman & Guillot Reference Showman and Guillot2002; Cooper & Showman Reference Cooper and Showman2005; Menou & Rauscher Reference Menou and Rauscher2009) but more recent models include a radiative transfer model and are therfore coupled radiative-dynamical models.

Because of the need to perform radiative transfer solutions for each grid point and time step, radiative transfer methods for GCMs generally need to be simplified compared with those used in the 1D models described earlier. Dobbs-Dixon & Lin (Reference Dobbs-Dixon and Lin2008) used a grey model described by a single mean opacity. Heng, Frierson, & Phillips (Reference Heng, Frierson and Phillips2011) and Rauscher & Menou (Reference Rauscher and Menou2012) use dual-band radiative transfer, dividing radiation into incoming shortwave radiation from the star, and outgoing longwave radiation from the planet. Showman et al. (Reference Showman, Fortney, Lian, Marley, Freedman, Knutson and Charbonneau2009) use the correlated-k method (see Section 4.3) with 30 wavelength bins. Dobbs-Dixon & Agol (Reference Dobbs-Dixon and Agol2013) use a similar set of 30 bins but use band-averaged opacities rather than the correlated-k method. The radiative transfer in all these cases uses a two-stream approximation. Amundsen et al. (Reference Amundsen, Baraffe, Tremblin, Manners, Hayek, Mayne and Acreman2014) has tested the accuracy of some of these approaches and find that correlated-k and two-stream methods give reasonable accuracy, but band-averaged opacities can lead to substantial errors.

A review of atmospheric circulation models for exoplanets is given by Showman, Cho, & Menou (Reference Showman, Cho, Menou and Seager2010). Features predicted by such models are the presence of a superrotating jet in the equatorial regions with wind velocities of 1–4 km/s. This can cause an eastward displacement of the hottest region from the substellar point which is consistent with observations of HD 189733b (Knutson et al. Reference Knutson2007a, Reference Knutson2009b).

Models that specifically aim to simulate the atmospheres of HD 189733b and HD 209458b have been given by Showman et al. (Reference Showman, Fortney, Lian, Marley, Freedman, Knutson and Charbonneau2009) and an example of the predicted temperature structure and winds is given in Figure 16 and show reasonable agreement with observed day-night phase variations in Spitzer photometry of HD 189733b (Knutson et al. Reference Knutson2007a, Reference Knutson2009b).

Figure 16. Temperature (colourscale in K) and winds (arrows) at the 30 mbar level for a 3D general circulation model simulation of the atmosphere of HD 189733b. (Figure 4, Showman, A.P. et al., Atmospheric Circulation of Hot Jupiters: Coupled Radiative-Dynamical General Circulation Model Simulations of HD 189733b and HD 209458b, The Astrophysical Journal, 699, 564. reproduced by permission of the AAS.)

Dobbs-Dixon & Agol (Reference Dobbs-Dixon and Agol2013) have used a 3D model of HD 189733b including wavelength dependent radiative transfer to make predictions of the transmission spectrum, dayside spectrum, and phase curves that are in good agreement with the observations.

4.1.4 3D models of brown dwarfs

Studies of atmospheric circulation in brown dwarfs have been made using 3D models and analytic theory (Showman & Kaspi Reference Showman and Kaspi2013) and shallow water models (Zhang & Showman Reference Zhang and Showman2014). These show atmospheric circulation with horizontal wind speeds up to 300 m s⁻¹, and vertical mixing that could help to explain the disequilibrium chemistry and patchy clouds near the L/T transition (see Section 2.5).

4.2.1 Equilibrim chemistry

Chemical models for brown dwarf and exoplanet atmospheres aim to predict the chemical composition in the atmosphere given the pressure, temperature and elemental abundances. Normally this is based on the assumption of chemical equilibrium. This can be achieved by solving a system of equations for the mass balance of each element and for the overall charge balance using the equilibrium constants of formation for each compound (e.g. Tsuji Reference Tsuji1973; Allard et al. Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001; Lodders & Fegley Reference Lodders and Fegley2002). An alternative, but equivalent, approach is that of minimisation of the total Gibbs free energy of the system (Sharp & Huebner Reference Sharp and Huebner1990; Sharp & Burrows Reference Sharp and Burrows2007).

In either case the required data is available in compilations such as the National Institute for Standards and Technology (NIST)-JANAF thermochemical Tables (Chase Reference Chase1998) and similar Tables such as Barin (Reference Barin1995) and Robie & Hemingway (Reference Robie and Hemingway1995). These tables list the equilibrium constants of formation K_f and Gibbs free energy of formation Δ _f G^o for a large number of compounds as a function of temperature. The two are related through

(3) \begin{equation} \Delta _fG^o = -RT\ln {K_f} \end{equation}

Where R is the gas constant. The required thermochemical data for gas phase species can also be derived from spectroscopic constants.

Chemical models predict the abundances of gas phase species, ionised species and the formation of liquid and solid condensates. The thermochemical models can also predict quantities such as the mean molecular weight, the specific heat and the adiabatic gradient, the latter two quantities being needed for mixing length convection theory.

4.2.2 Departures from equilibrium

Departures from equlibrium chemistry can occur as a result of photochemistry or vertical mixing if these processes occur at a faster rate than the collisional processes that tend to restore equilibrium. A non-equilibrium correction to the equilibrium abundances of CH₄/CO and NH₃/N₂ due to vertical mixing (Saumon et al. Reference Saumon, Marley, Lodders, Freedman and Martín2003) has been adopted to explain the observations of these species in brown dwarfs. A similar nonequilibrium treatement is used by Barman et al. (Reference Barman, Macintosh, Konopacky and Marois2011a) to model the exoplanet HR8799b. Cooper & Showman (Reference Cooper and Showman2006) have found that similar departures from CO/CH₄ equilibrium occur in tidally-locked hot-Jupiters.

Zahnle & Marley (Reference Zahnle and Marley2014) have explored the disequilibrium abundances of CH₄/CO and NH₃/N₂ in brown dwarfs and self-luminous giant planets using a chemical kinetic approach. They find that the low gravity of planets strongly discriminates against CH₄, and that in Jupiter mass planets CH₄ becomes more abundant than CO only for temperatures below about 400–600K depending on the effects of vertical mixing. Ammonia is also sensitive to gravity but insensitive to mixing making it a potetnial proxy for gravity.

Chemical models for hot Jupiter atmospheres using a chemical kinetic approach that can include the effects of photochemistry have been explored in a number of studies (e.g. Zahnle et al. Reference Zahnle, Marley, Freedman, Lodders and Fortney2009; Line, Liang, & Yung Reference Line, Liang and Yung2010; Line et al. Reference Line, Vasischt, Chen, Angerhausen and Yung2011; Moses et al. Reference Moses2011; Venot et al. Reference Venot, Hébrard, Agúndez, Dobrijevic, Selsis, Hersant, Iro and Bounaceur2012; Agúndez et al. Reference Agúndez, Parmentier, Venot, Hersant and Selsis2014) (see also review by Moses Reference Moses2014). There remain some differences between model predictions for species such as CH₄ and NH₃ due to uncertainties in reaction rates and transport parameters (see discussion in Moses Reference Moses2014 and Agúndez et al. Reference Agúndez, Parmentier, Venot, Hersant and Selsis2014), but generally these models show enhancements of a number of species in the upper atmosphere due to photochemical effects. Most of these models consider C, N and O containing species. The model by Zahnle et al. (Reference Zahnle, Marley, Freedman, Lodders and Fortney2009) includes sulfur species and explores the photochemical production of HS (mercapto) and S₂ as possible absorbers that could contribute to stratospheric heating.

4.3.1 Carbon dioxide (CO₂)

The Carbon Dioxide Spectroscopic Databank (CDSD Tashkun et al. Reference Tashkun, Perevalov, Teffo, Bykov and Lavrentieva2003) previously available in 296 K and 1 000 K versions is now available in a 4 000 K versionFootnote ⁴ containing lines to an intensity of 10⁻²⁷ cm molecule⁻¹ at 4 000 K for four isotopologues over the range 226–8310 cm⁻¹ (628 million lines).

New computed line lists for CO₂ and its isotopologues at 296K and 1 000K (the Ames-296K and Ames-1000K lists) have been described by Huang et al. (Reference Huang, Gamache, Freedman, Schwenke and Lee2013, Reference Huang, Freedman, Tashkun, Schwenke and Lee2014).

4.3.2 Ammonia (NH₃)

A computed line list for ammonia at temperatures up to 1 500 K and containing more than 1.1 billion lines for frequencies up to 12 000 cm⁻¹ (the BYTe list) is described by Yurchenko, Barber, & Tennyson (Reference Yurchenko, Barber and Tennyson2012).

Hargreaves, Li, & Bernath (Reference Hargreaves, Li and Bernath2011, Reference Hargreaves, Li and Bernath2012a) have provided line lists based on laboratory measurements of NH₃ lines at temperatures from 300 °C to 1 400 °C over the wavelength range from 740–4 000 cm⁻¹.

4.3.3 Methane (CH₄)

Methane has been the most problematic of the important species in exoplanet and brown dwarf atmospheres as far as line data is concerned. Significant recent progress has been made with modelling (e.g. Rey, Nikitin, & Tyuterev Reference Rey, Nikitin and Tyuterev2013; Nikitin, Rey, & Tyuterev Reference Nikitin, Rey and Tyuterev2013b; Yurchenko et al. Reference Yurchenko, Tennyson, Barber and Thiel2013) and a large computed line list for hot methane has very recently been developed (Yurchenko & Tennyson Reference Yurchenko and Tennyson2014)Footnote ⁵ . Yurchenko et al. (Reference Yurchenko, Bailey, Hollis and Tinnetti2014) have shown that using this line list it is possible to obtain good model fits to the methane bands in the near infrared spectra of brown dwarfs that could not be fitted with older line lists, such as those based on the Spherical Top Data System software (STDS Wenger & Champion Reference Wenger and Champion1998). Another computed line list for hot methane has been reported by Rey, Nikitin, & Tyuterev (Reference Rey, Nikitin and Tyuterev2014) but is limited to wavelengths longer than 2 μm.

Much improved line lists for the 1.26–1.71 μm region at temperatures from 80–300 K have been developed recently from extensive laboratory measurements at cryogenic and room temperature (Wang et al. Reference Wang, Mondelain, Kassi and Campargue2012; Campargue et al. Reference Campargue, Leshchishina, Wang, Mondelain, Kassi and Nikitin2012a, Reference Campargue, Leshchishina, Wang, Mondelain and Kassi2013). These lists, and earlier versions of them, have been used successfully for modelling the spectra of Titan (Bailey, Ahlsved, & Meadows Reference Bailey, Ahlsved and Meadows2011; de Bergh et al. Reference de Bergh2012; Campargue et al. Reference Campargue2012b) and Uranus (Irwin et al. Reference Irwin2012; Bott, Kedziora-Chudczer, & Bailey Reference Bott, Kedziora-Chudczer, Bailey, Short and Cairns2013). An improved low temperature line list has also been developed for the 2 μm region (Daumont et al. Reference Daumont2013). These lists have been incorporated into the new 2012 edition of the HITRAN databaseFootnote ⁶ recently released.

Empirical line lists for methane measured at temperatures from 300–1 400 °C over the wavelength range from 2.0–10.4 μm have been provided by Hargreaves et al. (Reference Hargreaves, Beale, Michaux, Irfan and Bernath2012b).

4.3.4 SiO and HCN/HNC

New line lists for SiO (Barton, Yurchenko, & Tennyson Reference Barton, Yurchenko and Tennyson2013) and HCN/HNC (Barber et al. Reference Barber, Strange, Hill, Polyansky, Mellau, Yurchenko and Tennyson2014) have recently been published by the ExoMol group.

4.3.5 Collision induced absorptions (CIA)

The collision induced absorption of H₂ - H₂ and H₂ - He pairs are important contributors to the opacity of brown dwarfs and planets. Updated data on these absorptions have recently been provided by Abel et al. (Reference Abel, Frommhold, Li and Hunt2011, Reference Abel, Frommhold, Li and Hunt2012) as described in Saumon et al. (Reference Saumon, Marley, Abel, Frommhold and Freedman2012). This data as well as other CIA datasets have been recently made available in a new section of the HITRAN database (Richard et al. Reference Richard2012).

4.4.1 Clouds in brown dwarfs

Two limiting cases were considered in the COND and DUSTY models of Allard et al. (Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001). The COND models include condensate formation, which alters the chemistry by depleting elements from the gas, but did not include any contribution of the condensates to the opacity. In the DUSTY models the condensed material is assumed to remain in place in equilibrium with the gas phase and form clouds of small dust grains. The DUSTY models were found to be a good representation of late-M and early-L dwarfs, but at cooler temperatures they produce weakening of spectral features and increasingly red colours in disagreement with the observations of L-T transition objects.

The cloud-free COND models were found to be a fairly good representation of mid to late T dwarfs, indicating that gravitational settling has largely removed dust from the atmospheres in these cases. However, neither of these two models could account for the late-L to early T dwarfs. A number of cloud models have now been developed that aim to reproduce the behaviour of clouds through the full brown dwarf spectral sequence.

In the Unified Cloudy Model (Tsuji Reference Tsuji2002, Reference Tsuji2005), clouds are assumed to be restricted to a small range of temperatures between the condensation temperature T_cond and a critical temperature T_cr . Below the critical temperature it is assumed that grains will grow to such a size that they will rapidly precipitate under gravity. A fixed particle size (r = 0.01 μm) is used in the clouds. The critical temperature T_cr is an adjustable parameter, with values in the range 1 700–1 900 K providing a reasonable match to the observations.

Burrows, Sudarsky, & Hubeny (Reference Burrows, Sudarsky and Hubeny2006) describe a cloud model that similarly restricts the cloud extent but includes an exponential decay in cloud particle density at the upper and lower edges of the cloud. They investigate the effects of various cloud parameters and conclude that cloud particle sizes of 50–100 μm fit the data best. This is much larger than the grain sizes used in most other models which are around 1 μm or smaller.

Ackerman & Marley (Reference Ackerman and Marley2001) describe a cloud model based on a balance between turbulent diffusion and sedimentation in horizontally uniform cloud decks. The model involves a scaling factor f_sed that describes the efficiency of sedimentation and typically ranges from 1 to 5. Small f_sed values produce thicker clouds and match observations of L dwarfs and higher values are found for later type T dwarfs (Stephens et al. Reference Stephens2009).

The BT-Settl models (Allard et al. Reference Allard, Allard, Homeier, Kielkopf, McCaughrean and Spiegelman2007, Reference Allard, Homeier, Freytag and Sharp2012) use a cloud treatment based on a model for cloud microphysics from analysis of solar system atmospheres (Rossow Reference Rossow1978) that predicts timescales for condensation, sedimentation and coagulation. These are compared with the turbulent mixing timescale to predict grain densities and sizes.

Woitke & Helling (Reference Woitke and Helling2003, Reference Woitke and Helling2004) and Helling & Woitke (Reference Helling and Woitke2006) have developed a kinetic (non-equilibrium) model for the nucleation, accretion, gravitational settling and evaporation of dust grains. A version of this cloud model has been integrated with the PHOENIX stellar atmosphere code (Hauschildt & Baron Reference Hauschildt and Baron1999) to provide the DRIFT-PHOENIX models for substellar atmospheres (Helling et al. Reference Helling, Dehn, Woitke and Hauschildt2008a).

A more detailed description of some of these different cloud models and a comparison of their predictions in test cases can be found in Helling et al. (Reference Helling2008b).

A specific aim of these models is to explain the changes that occur in brown dwarfs at the L/T transition as discussed in Section 2. Figure 17 shows that the BT-Settl model (and other cloud models make simiar predictions) can explain the general trend seen in the near-IR colour magnitude diagram of a swing from red to blue colours at the L/T transition. The models achieve this mostly because the cloud has a limited extent in temperature, and so for cooler models the clouds drop to layers below the photosphere where the effect on the spectra and colours become small.

Figure 17. Colour magintude diagram using the same data as Figure 5 compared with the predictions of model atmospheres using different cloud models. The BT-COND and BT-DUSTY models are updated version of the COND and DUSTY models of Allard et al. (Reference Allard, Hauschildt, Alexander, Tamanai and Schweitzer2001) with more modern opacities. The BT-SETTL model is described by Allard et al. (Reference Allard, Allard, Homeier, Kielkopf, McCaughrean and Spiegelman2007, Reference Allard, Homeier, Freytag and Sharp2012). The plotted lines are predicted synthetic magnitudes for the isochromes of Baraffe et al. (Reference Baraffe, Chabrier, Barman, Allard and Hauschildt2003) and Chabrier et al. (Reference Chabrier, Baraffe, Allard and Hauschildt2000a). For BT-SETTL 1, 3 and 5 Gyr isochrones are plotted as dotted, solid and dashed lines. For COND and DUSTY the 3 Gyr isochrone only is plotted.

However, all current models fail to match the details of the L/T transition. As can be seen in Figure 7 models fail to reproduce the sharpness of the transition as a function of effective temperature. Models also fail to reproduce the J-band brightening (see Section 2.3). The BT-Settl model also predicts J − K colours that continue to get bluer with lower effective temperatures, while observations show fairly constant J − K for mid to late T dwarfs (Figures 7 and 17).

Cloud species that condense at lower temperatures (including Cr, MnS, Na₂S, ZnS and KCl) are considered by Morley et al. (Reference Morley, Fortney, Marley, Channon, Saumon and Leggett2012), and found to be helpful in explaining the colours and spectra of late-T and Y dwarfs (Leggett et al. Reference Leggett, Morley, Marley, Saumon, Fortney and Visscher2013).