Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sánchez, B. O.
Brout, D.
Vincenzi, M.
Sako, M.
Herner, K.
Kessler, R.
Davis, T. M.
Scolnic, D.
Acevedo, M.
Lee, J.
Möller, A.
Qu, H.
Kelsey, L.
Wiseman, P.
Armstrong, P.
Rose, B.
Camilleri, R.
Chen, R.
Galbany, L.
Kovacs, E.
Lidman, C.
Popovic, B.
Smith, M.
Shah, P.
Sullivan, M.
Toy, M.
Abbott, T. M. C.
Aguena, M.
Allam, S.
Alves, O.
Annis, J.
Asorey, J.
Avila, S.
Bacon, D.
Brooks, D.
Burke, D. L.
Carnero Rosell, A.
Carollo, D.
Carretero, J.
da Costa, L. N.
Castander, F. J.
Desai, S.
Diehl, H. T.
Duarte, J.
Everett, S.
Ferrero, I.
Flaugher, B.
Frieman, J.
García-Bellido, J.
Gatti, M.
Gaztanaga, E.
Giannini, G.
Glazebrook, K.
González-Gaitán, S.
Gruendl, R. A.
Gutierrez, G.
Hinton, S. R.
Hollowood, D. L.
Honscheid, K.
James, D. J.
Kuehn, K.
Lahav, O.
Lee, S.
Lewis, G. F.
Lin, H.
Marshall, J. L.
Mena-Fernández, J.
Miquel, R.
Myles, J.
Nichol, R. C.
Ogando, R. L. C.
Palmese, A.
Pereira, M. E. S.
Pieres, A.
Plazas Malagón, A. A.
Porredon, A.
Romer, A. K.
Sanchez, E.
Sanchez Cid, D.
Sevilla-Noarbe, I.
Suchyta, E.
Swanson, M. E. C.
Tarle, G.
Tucker, B. E.
Tucker, D. L.
Vikram, V.
Walker, A. R.
and
Weaverdyck, N.
2024.
The Dark Energy Survey Supernova Program: Light Curves and 5 Yr Data Release.
The Astrophysical Journal,
Vol. 975,
Issue. 1,
p.
5.
Abbott, DES Collaboration: T. M. C.
Acevedo, M.
Aguena, M.
Alarcon, A.
Allam, S.
Alves, O.
Amon, A.
Andrade-Oliveira, F.
Annis, J.
Armstrong, P.
Asorey, J.
Avila, S.
Bacon, D.
Bassett, B. A.
Bechtol, K.
Bernardinelli, P. H.
Bernstein, G. M.
Bertin, E.
Blazek, J.
Bocquet, S.
Brooks, D.
Brout, D.
Buckley-Geer, E.
Burke, D. L.
Camacho, H.
Camilleri, R.
Campos, A.
Carnero Rosell, A.
Carollo, D.
Carr, A.
Carretero, J.
Castander, F. J.
Cawthon, R.
Chang, C.
Chen, R.
Choi, A.
Conselice, C.
Costanzi, M.
da Costa, L. N.
Crocce, M.
Davis, T. M.
DePoy, D. L.
Desai, S.
Diehl, H. T.
Dixon, M.
Dodelson, S.
Doel, P.
Doux, C.
Drlica-Wagner, A.
Elvin-Poole, J.
Everett, S.
Ferrero, I.
Ferté, A.
Flaugher, B.
Foley, R. J.
Fosalba, P.
Friedel, D.
Frieman, J.
Frohmaier, C.
Galbany, L.
García-Bellido, J.
Gatti, M.
Gaztanaga, E.
Giannini, G.
Glazebrook, K.
Graur, O.
Gruen, D.
Gruendl, R. A.
Gutierrez, G.
Hartley, W. G.
Herner, K.
Hinton, S. R.
Hollowood, D. L.
Honscheid, K.
Huterer, D.
Jain, B.
James, D. J.
Jeffrey, N.
Kasai, E.
Kelsey, L.
Kent, S.
Kessler, R.
Kim, A. G.
Kirshner, R. P.
Kovacs, E.
Kuehn, K.
Lahav, O.
Lee, J.
Lee, S.
Lewis, G. F.
Li, T. S.
Lidman, C.
Lin, H.
Malik, U.
Marshall, J. L.
Martini, P.
Mena-Fernández, J.
Menanteau, F.
Miquel, R.
Mohr, J. J.
Mould, J.
Muir, J.
Möller, A.
Neilsen, E.
Nichol, R. C.
Nugent, P.
Ogando, R. L. C.
Palmese, A.
Pan, Y.-C.
Paterno, M.
Percival, W. J.
Pereira, M. E. S.
Pieres, A.
Plazas Malagón, A. A.
Popovic, B.
Porredon, A.
Prat, J.
Qu, H.
Raveri, M.
Rodríguez-Monroy, M.
Romer, A. K.
Roodman, A.
Rose, B.
Sako, M.
Sanchez, E.
Sanchez Cid, D.
Schubnell, M.
Scolnic, D.
Sevilla-Noarbe, I.
Shah, P.
Smith, J. Allyn.
Smith, M.
Soares-Santos, M.
Suchyta, E.
Sullivan, M.
Suntzeff, N.
Swanson, M. E. C.
Sánchez, B. O.
Tarle, G.
Taylor, G.
Thomas, D.
To, C.
Toy, M.
Troxel, M. A.
Tucker, B. E.
Tucker, D. L.
Uddin, S. A.
Vincenzi, M.
Walker, A. R.
Weaverdyck, N.
Wechsler, R. H.
Weller, J.
Wester, W.
Wiseman, P.
Yamamoto, M.
Yuan, F.
Zhang, B.
and
Zhang, Y.
2024.
The Dark Energy Survey: Cosmology Results with ∼1500 New High-redshift Type Ia Supernovae Using the Full 5 yr Data Set.
The Astrophysical Journal Letters,
Vol. 973,
Issue. 1,
p.
L14.
Vincenzi, M.
Brout, D.
Armstrong, P.
Popovic, B.
Taylor, G.
Acevedo, M.
Camilleri, R.
Chen, R.
Davis, T. M.
Lee, J.
Lidman, C.
Hinton, S. R.
Kelsey, L.
Kessler, R.
Möller, A.
Qu, H.
Sako, M.
Sanchez, B.
Scolnic, D.
Smith, M.
Sullivan, M.
Wiseman, P.
Asorey, J.
Bassett, B. A.
Carollo, D.
Carr, A.
Foley, R. J.
Frohmaier, C.
Galbany, L.
Glazebrook, K.
Graur, O.
Kovacs, E.
Kuehn, K.
Malik, U.
Nichol, R. C.
Rose, B.
Tucker, B. E.
Toy, M.
Tucker, D. L.
Yuan, F.
Abbott, T. M. C.
Aguena, M.
Alves, O.
Allam, S. S.
Andrade-Oliveira, F.
Annis, J.
Bacon, D.
Bechtol, K.
Bernstein, G. M.
Brooks, D.
Burke, D. L.
Carnero Rosell, A.
Carretero, J.
Castander, F. J.
Conselice, C.
da Costa, L. N.
Pereira, M. E. S.
Desai, S.
Diehl, H. T.
Doel, P.
Ferrero, I.
Flaugher, B.
Friedel, D.
Frieman, J.
García-Bellido, J.
Gatti, M.
Giannini, G.
Gruen, D.
Gruendl, R. A.
Hollowood, D. L.
Honscheid, K.
Huterer, D.
James, D. J.
Kuropatkin, N.
Lahav, O.
Lee, S.
Lin, H.
Marshall, J. L.
Mena-Fernández, J.
Menanteau, F.
Miquel, R.
Palmese, A.
Pieres, A.
Plazas Malagón, A. A.
Porredon, A.
Romer, A. K.
Roodman, A.
Sanchez, E.
Sanchez Cid, D.
Schubnell, M.
Sevilla-Noarbe, I.
Suchyta, E.
Swanson, M. E. C.
Tarle, G.
To, C.
Walker, A. R.
Weaverdyck, N.
and
Yamamoto, M.
2024.
The Dark Energy Survey Supernova Program: Cosmological Analysis and Systematic Uncertainties.
The Astrophysical Journal,
Vol. 975,
Issue. 1,
p.
86.
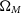 $\Omega_{M}$ and 0.07 in w. This divergence is most impactful for analyses of cosmological tensions, but its impact is mitigated when combining supernovae with other cross-cutting cosmological probes, such as the cosmic microwave background.
$\Omega_{M}$ and 0.07 in w. This divergence is most impactful for analyses of cosmological tensions, but its impact is mitigated when combining supernovae with other cross-cutting cosmological probes, such as the cosmic microwave background.


