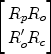The aesthetic preferences of a group of persons are obtained from their orders of sets of pictures and patterns according to “liking.” The same pictures are ordered independently by a team of experts, according to certain artistic criteria such as naturalism, composition, color, rhythm, etc. The orders of preference and orders according to the criteria are compared by correlation and matrices of correlation formed from (1) correlations between the persons' orders of preference; (2) correlations between the orders of preference and orders according to artistic criteria; and (3) correlations between the criterion orders. These matrices are symbolised by Rp, R0, and Rc, respectively, and combined to form a single matrix \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\left[ \begin{gathered}R_p R_o\hfill \\R'_o R_c\hfill \\ \end{gathered}\right]$$\end{document}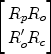
. Three interesting analyses of this matrix are suggested: Analysis of the whole matrix into its factors and rotation of the factors about the criteria, regression estimates of individual preferences on the artistic criteria, and regression estimates of the person preference factors on the same criteria. Theoretical conditions and consequences of these analyses are then discussed by the use of matrix notation.