Published online by Cambridge University Press: 01 January 2025
In the social sciences we are often interested in comparing models specified by parametric equality or inequality constraints. For instance, when examining three group means {μ1,μ2,μ3}\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\{ \mu _1, \mu _2, \mu _3\}$$\end{document}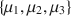 through an analysis of variance (ANOVA), a model may specify that μ1<μ2<μ3\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\mu _1<\mu _2<\mu _3$$\end{document}
through an analysis of variance (ANOVA), a model may specify that μ1<μ2<μ3\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\mu _1<\mu _2<\mu _3$$\end{document}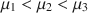 , while another one may state that {μ1=μ3}<μ2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\{ \mu _1=\mu _3\} <\mu _2$$\end{document}
, while another one may state that {μ1=μ3}<μ2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\{ \mu _1=\mu _3\} <\mu _2$$\end{document}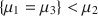 , and finally a third model may instead suggest that all means are unrestricted. This is a challenging problem, because it involves a combination of nonnested models, as well as nested models having the same dimension. We adopt an objective Bayesian approach, requiring no prior specification from the user, and derive the posterior probability of each model under consideration. Our method is based on the intrinsic prior methodology, suitably modified to accommodate equality and inequality constraints. Focussing on normal ANOVA models, a comparative assessment is carried out through simulation studies. We also present an application to real data collected in a psychological experiment.
, and finally a third model may instead suggest that all means are unrestricted. This is a challenging problem, because it involves a combination of nonnested models, as well as nested models having the same dimension. We adopt an objective Bayesian approach, requiring no prior specification from the user, and derive the posterior probability of each model under consideration. Our method is based on the intrinsic prior methodology, suitably modified to accommodate equality and inequality constraints. Focussing on normal ANOVA models, a comparative assessment is carried out through simulation studies. We also present an application to real data collected in a psychological experiment.
Electronic supplementary material The online version of this article (doi:10.1007/s11336-016-9516-y) contains supplementary material, which is available to authorized users.