Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-08T10:11:44.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficient Alpha and the Internal Structure of Tests

Published online by Cambridge University Press:  01 January 2025

Lee J. Cronbach
Lee J. Cronbach*
Affiliation:
University of Illinois
Get access Rights & Permissions [Opens in a new window]

Abstract

A general formula (α) of which a special case is the Kuder-Richardson coefficient of equivalence is shown to be the mean of all split-half coefficients resulting from different splittings of a test. α is therefore an estimate of the correlation between two random samples of items from a universe of items like those in the test. α is found to be an appropriate index of equivalence and, except for very short tests, of the first-factor concentration in the test. Tests divisible into distinct subtests should be so divided before using the formula. 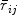The index \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\bar r_{ij} $$\end{document}, derived from α, is shown to be an index of inter-item homogeneity. Comparison is made to the Guttman and Loevinger approaches. Parallel split coefficients are shown to be unnecessary for tests of common types. In designing tests, maximum interpretability of scores is obtained by increasing the first-factor concentration in any separately-scored subtest and avoiding substantial group-factor clusters within a subtest. Scalability is not a requisite.

Type
Original Paper
Information
Psychometrika , Volume 16 , Issue 3 , September 1951 , pp. 297 - 334
Copyright
Copyright © 1951 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

The assistance of Dora Damrin and Willard Warrington is gratefully acknowledged. Miss Damrin took major responsibility for the empirical studies reported. This research was supported by the Bureau of Research and Service, College of Education.

References

Brogden, H. E. Variation in test validity with variation in the distribution of item difficulties, number of items, and degree of their intercorrelation. Psychometrika, 1946, 11, 197–214.CrossRefGoogle ScholarPubMed
Brown, W. Some experimental results in the correlation of mental abilities. Brit. J. Psychol., 1910, 3, 296–322.Google Scholar
Brownell, W. A. On the accuracy with which reliability may be measured by correlating test halves. J. exper. Educ., 1933, 1, 204–215.Google Scholar
Burt, C. The influence of differential weighting. Brit. J. Psychol., Stat. Sect., 1950, 3, 105–128.CrossRefGoogle Scholar
Clark, E. L. Methods of splitting vs. samples as sources of instability in test-reliability coefficients. Harvard educ. Rev., 1949, 19, 178–182.Google Scholar
Coombs, C. H. The concepts of reliability and homogeneity. Educ. psychol. Meas., 1950, 10, 43–56.CrossRefGoogle Scholar
Cronbach, L. J. On estimates of test reliability. J. educ. Psychol., 1943, 34, 485–494.CrossRefGoogle Scholar
Cronbach, L. J. A case study of the split-half reliability coefficient. J. educ. Psychol., 1946, 37, 473–480.Google ScholarPubMed
Cronbach, L. J. Test “reliability”: its meaning and determination. Psychometrika, 1947, 12, 1–16.CrossRefGoogle ScholarPubMed
Dressel, P. L. Some remarks on the Kuder-Richardson reliability coefficient. Psychometrika, 1940, 5, 305–310.CrossRefGoogle Scholar
Ferguson, G. The factorial interpretation of test difficulty. Psychometrika, 1941, 6, 323–329.CrossRefGoogle Scholar
Ferguson, G. The reliability of mental tests, London: Univ. of London Press, 1941.Google Scholar
Festinger, L. The treatment of qualitative data by “scale analysis.”. Psychol. Bull., 1947, 44, 149–161.CrossRefGoogle ScholarPubMed
Goodenough, F. L. A critical note on the use of the term “reliability” in mental measurement. J. educ. Psychol., 1936, 27, 173–178.CrossRefGoogle Scholar
Guilford, J. P. Army Air Forces Aviation Psychology Program, Washington: U. S. Govt. Print. Off., 1947.Google Scholar
Guilford, J. P. Fundamental statistics in psychology and education Second ed.,, New York: McGraw-Hill, 1950.Google Scholar
Guilford, J. P. Michael, W. B. Changes in common-factor loadings as tests are altered homogeneously in length. Psychometrika, 1950, 15, 237–249.CrossRefGoogle ScholarPubMed
Gulliksen, H. Theory of mental tests, New York: Wiley, 1950.CrossRefGoogle Scholar
Guttman, L. A basis for analyzing test-retest reliability. Psychometrika, 1945, 10, 255–282.CrossRefGoogle ScholarPubMed
Hoyt, C. Test reliability estimated by analysis of variance. Psychometrika, 1941, 6, 153–160.Google Scholar
Humphreys, L. G. Test homogeneity and its measurement. Amer. Psychologist, 1949, 4, 245–245.Google Scholar
Jackson, R. W. and Ferguson, G. A.Studies on the reliability of tests. Bull. No. 12, Dept. of Educ. Res., University of Toronto, 1941.Google Scholar
Kelley, T. L. Note on the reliability of a test: a reply to Dr. Crum's criticism. J. educ. Psychol., 1924, 15, 193–204.CrossRefGoogle Scholar
Kelley, T. L. Statistical method, New York: Macmillan, 1924.Google Scholar
Kelley, T. L. The reliability coefficient. Psychometrika, 1942, 7, 75–83.CrossRefGoogle Scholar
Kuder, G. F. Richardson, M. W. The theory of the estimation of test reliability. Psychometrika, 1937, 2, 151–160.CrossRefGoogle Scholar
Loevinger, J. A systematic approach to the construction and evaluation of tests of ability. Psychol. Monogr., 1947, 61, 4.CrossRefGoogle Scholar
Loevinger, J. The technic of homogeneous tests compared with some aspects of “scale analysis” and factor analysis. Psychol. Bull., 1948, 45, 507–529.Google ScholarPubMed
Mosier, C. I. A short cut in the estimation of split-halves coefficients. Educ. psychol. Meas., 1941, 1, 407–408.CrossRefGoogle Scholar
Richardson, M. Combination of measures. In Horst, P.(Eds.), The prediction of personal adjustment (pp. 379–401). New York: Social Science Res. Council, 1941.Google Scholar
Rulon, P. J. A simplified procedure for determining the reliability of a test by split-halves. Harvard educ. Rev., 1939, 9, 99–103.Google Scholar
Shannon, C. E. The mathematical theory of communication, Urbana: Univ. of Ill. Press, 1949.Google Scholar
Spearman, C. Correlation calculated with faulty data. Brit. J. Psychol., 1910, 3, 271–295.Google Scholar
Stouffer, S. A. Measurement and prediction, Princeton: Princeton Univ. Press, 1950.Google Scholar
Thurstone, L. L. Thurstone, T. G. Factorial studies of intelligence (pp. 37–37). Chicago: Univ. of Chicago Press, 1941.Google Scholar
Tucker, L. R. Maximum validity of a test with equivalent items. Psychometrika, 1946, 11, 1–13.CrossRefGoogle ScholarPubMed
Vernon, P. E. An application of factorial analysis to the study of test items. Brit. J. Psychol., Stat. Sec., 1950, 3, 1–15.CrossRefGoogle Scholar
Wherry, R. J. Gaylord, R. H. The concept of test and item reliability in relation to factor pattern. Psychometrika, 1943, 8, 247–264.CrossRefGoogle Scholar
Woodbury, M. A.On the standard length of a test. Res. Bull. 50–53, Educ. Test. Service, 1950.CrossRefGoogle Scholar