Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-05T14:58:04.243Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extension of the Partial Credit Model with an Application to the Measurement of Change

Published online by Cambridge University Press:  01 January 2025

Gerhard H. Fischer  and
Ivo Ponocny
Gerhard H. Fischer*
Affiliation:
University of Vienna
Ivo Ponocny
Affiliation:
University of Vienna
*
Requests for reprints or for the LPCM software (please send a formatted 3 1/2 inch diskette) should be directed to Gerhard H. Fischer, Institut für Psychologic, Liebiggasse 5, A-1010 Wien (Vienna), Austria, e-mail [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

The partial credit model is considered under the assumption of a certain linear decomposition of the item × category parameters δih into “basic parameters” αj. This model is referred to as the “linear partial credit model”. A conditional maximum likelihood algorithm for estimation of the αj is presented, based on (a) recurrences for the combinatorial functions involved, and (b) using a “quasi-Newton” approach, the so-called Broyden-Fletcher-Goldfarb-Shanno (BFGS) method; (a) guarantees numerically stable results, (b) avoids the direct computation of the Hesse matrix, yet produces a sequence of certain positive definite matrices Bk, k = 1, 2, ..., converging to the asymptotic variance-covariance matrix of the \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \alpha _j $$\end{document}. 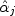The practicality of these numerical methods is demonstrated both by means of simulations and of an empirical application to the measurement of treatment effects in patients with psychosomatic disorders.

Keywords

Partial credit modelRasch modelitem response theorymeasurement of changeassessment of treatment effects
Type
Original Paper
Information
Psychometrika , Volume 59 , Issue 2 , June 1994 , pp. 177 - 192
Copyright
Copyright © 1994 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors thank one anonymous reviewer for his constructive comments. Moreover, they thankfully acknowledge financial support by the Österreichische Nationalbank (Austrian National Bank) under Grant No. 3720.

References

Andersen, E. B. (1983). A general latent structure model for contingency table data. In Wainer, H., Messik, S. (Eds.), Principals of modern psychological measurement (pp. 117–138). Hillsdale/NJ: Erlbaum.Google Scholar
Andrich, D. (1978). A rating formulation for ordered response categories. Psychometrika, 43, 561–573.CrossRefGoogle Scholar
Andrich, D. (1978). Application of a psychometric rating model to ordered categories which are scored with successive integers. Applied Psychological Measurement, 2, 581–594.CrossRefGoogle Scholar
Armijo, L. (1966). Minimization of functions having Lipschitz-continuous first partial derivatives. Pacific Journal of Mathematics, 16, 1–3.CrossRefGoogle Scholar
Churchhouse, R. F. (1981). Handbook of applicable mathematics, Vol. III, Chichester—New York: J. Wiley.Google Scholar
Fischer, G. H. (1972). A measurement model for the effect of mass-media. Acta Psychologica, 36, 207–220.CrossRefGoogle Scholar
Fischer, G. H. (1974). Einfürhrung in die Theorie psychologischer Tests [Introduction to mental test theory], Bern: Huber.Google Scholar
Fischer, G. H. (1977). Some probabilistic models for the description of attitudinal and behavioral changes under the influence of mass communication. In Kempf, W. F., Repp, B. (Eds.), Mathematical models for social psychology (pp. 102–151). Bern: Huber.Google Scholar
Fischer, G. H. (1989). An IRT-based model for dichotomous longitudinal data. Psychometrika, 54, 599–624.CrossRefGoogle Scholar
Fischer, G. H. (1991). A new methodology for the assessment of treatment effects. Evaluación Psicológical Psychological Assessment, 7, 117–147.Google Scholar
Fischer, G. H., Allerup, P. (1968). Rechentechnische Fragen zu Raschs eindimensionalem Modell [Numerical problems in the unidimensional model of Rasch]. In Fischer, G. H. (Eds.), Psychologische Test-theorie (pp. 269–280). Bern: Huber.Google Scholar
Fischer, G. H., Parzer, P. (1991). An extension of the rating scale model with an application to the measurement of treatment effects. Psychometrika, 56, 637–651.CrossRefGoogle Scholar
Fischer, G. H., Parzer, P. (1991). LRSM: Parameter estimation for the linear rating scale model. Applied Psychological Measurement, 15, 138–138.CrossRefGoogle Scholar
Glas, C. A. W. (1989). Contributions to estimating and testing Rasch models, The Hague: CIP-Gegevens Koninklijke Bibliotheek.Google Scholar
Glas, C. A. W., Verhelst, N. D. (1989). Extensions of the partial credit model. Psychometrika, 54, 635–659.CrossRefGoogle Scholar
Gustafsson, J.-E. (1980). A solution of the conditional estimation problem for long tests in the Rasch model for dichotomous items. Educational and Psychological Measurement, 40, 377–385.CrossRefGoogle Scholar
Jacobsen, M. (1989). Existence and unicity of MLEs in discrete exponential family distributions. Scandinavian Journal of Statistics, 16, 335–349.Google Scholar
Kosmol, P. (1989). methoden zur numerischen Behandlung nichtlinearer Gleichungen und Optimierungsaufgaben, Stuttgart: Teubner.CrossRefGoogle Scholar
Masters, G. N. (1982). A Rasch model for partial credit scoring. Psychometrika, 47, 149–174.CrossRefGoogle Scholar
Rasch, G. (1961). On general laws and the meaning of measurement in psychology. Proceedings of the IV. Berkeley symposium on mathematical statistics and probability, Vol. 4 (pp. 321–333). Berkeley: University of California Press.Google Scholar
Rasch, G. (1965). Statistisk seminar [Statistical seminar], Cogenhague: University of Copenhague, Department of Mathematical Statistics.Google Scholar
Rasch, G. (1967). An informal report on a theory of objectivity in comparisons. In van der Kamp, L. J. Th., Vlek, C. A. J. (Eds.), Psychological measurement theory (pp. 1–19). Leyden: University of Leyden.Google Scholar
Widowitz, E. (1987). Der Effekt autogenen Trainings bei funktionellen Erkrankungen [The effect of “autogenous training” on the functional syndrome], Vienna: University Vienna, Department of Psychology.Google Scholar
Wright, B. D., Masters, G. N. (1982). Rating scale analysis: Rasch measurement, Chicago: Mesa Press.Google Scholar
v. Zerssen, D. (1976). Klinische Selbstbeurteilungsskalen (KSb-S) aus dem Münchner Psychiatrischen Informations-System (PSYCHIS München) [The clinical self-rating scales (KSb-S) of the “Munich Psychiatric Information System” (PSYCHIS)], Weinheim: Beltz.Google Scholar