Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-24T13:40:07.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularized Variational Estimation for Exploratory Item Factor Analysis

Published online by Cambridge University Press:  01 January 2025

April E. Cho ,
Jiaying Xiao ,
Chun Wang  and
Gongjun Xu Open the ORCID record for Gongjun Xu [Opens in a new window]
April E. Cho
Affiliation:
University of Michigan
Jiaying Xiao
Affiliation:
University of Washington
Chun Wang*
Affiliation:
University of Washington
Gongjun Xu*
Affiliation:
University of Michigan
*
Email: [email protected]
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Item factor analysis (IFA), also known as Multidimensional Item Response Theory (MIRT), is a general framework for specifying the functional relationship between respondents’ multiple latent traits and their responses to assessment items. The key element in MIRT is the relationship between the items and the latent traits, so-called item factor loading structure. The correct specification of this loading structure is crucial for accurate calibration of item parameters and recovery of individual latent traits. This paper proposes a regularized Gaussian Variational Expectation Maximization (GVEM) algorithm to efficiently infer item factor loading structure directly from data. The main idea is to impose an adaptive L1\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$L_1$$\end{document}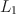-type penalty to the variational lower bound of the likelihood to shrink certain loadings to 0. This new algorithm takes advantage of the computational efficiency of GVEM algorithm and is suitable for high-dimensional MIRT applications. Simulation studies show that the proposed method accurately recovers the loading structure and is computationally efficient. The new method is also illustrated using the National Education Longitudinal Study of 1988 (NELS:88) mathematics and science assessment data.

Keywords

latent variable selectionmultidimensional item response theoryvariational inferenceexpectation-maximizationlassoadaptive lasso
Type
Original Research
Information
Psychometrika , Volume 89 , Issue 1 , March 2024 , pp. 347 - 375
Copyright
Copyright © 2022 The Author(s) under exclusive licence to The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Albert, J.H.. (1992). Bayesian estimation of normal ogive item response curves using gibbs sampling. Journal of Educational Statistics, 17 3251–269.CrossRefGoogle Scholar
Beck, A, Teboulle, M. (2009). A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2 1182–202.CrossRefGoogle Scholar
Bishop, C. M. (2006). Pattern recognition and machine learning. Springer.Google Scholar
Bock, R.D., Gibbons, R, Muraki, E. (1988). Full-information item factor analysis. Applied Psychological Measurement, 12 3261–280.CrossRefGoogle Scholar
Breheny, P, Huang, J. (2011). Coordinate descent algorithm for nonconvex penalized regression, with application to biological feature selection. The Annals of Applied Statistics, 74, 5232–253.Google Scholar
Browne, M.W.. (2001). An overview of analytic rotation in exploratory factor analysis. Multivariate Behavioral Research, 36 1111–150.CrossRefGoogle Scholar
Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis-Hastings Robbins-Monro algorithm. Psychometrika, 75 133–57.CrossRefGoogle Scholar
Cai, L. (2010). Metropolis-Hastings Robbins-Monro algorithm for confirmatory item factor analysis. Journal of Educational and Behavioral Statistics, 35 3307–335.CrossRefGoogle Scholar
Cattell, R.B.. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1 2245–276.CrossRefGoogle ScholarPubMed
Chen, Y, Li, X, Zhang, S. (2019). Joint maximum likelihood estimation for high-dimensional exploratory item factor analysis. Psychometrika, 84 1124–146.CrossRefGoogle ScholarPubMed
Cho, A.E., Wang, C, Zhang, X, Xu, G. (2021). Gaussian variational estimation for multidimensional item response theory. British Journal of Mathematical and Statistical Psychology, 4, 7452–85.Google Scholar
Costello, A.B., Osborne, J. (2005). Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Practical Assessment, Research, and Evaluation, 10 1–13 7.Google Scholar
Domke, J. , & Sheldon, D. (2018). Importance weighting and variational inference. In Proceedings of the 32nd international conference on neural information processing systems (pp. 4475–4484).Google Scholar
Embretson, S. E., & Reise, S. P. (2000). Psychometric methods: Item response theory for psychologists. Lawrence Erlbaum Associates.Google Scholar
Fabrigar, L. R., & Wegener, D. T. (2011). Exploratory factor analysis. Oxford University Press.CrossRefGoogle Scholar
Fan, J, Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 2, 961348–1360.Google Scholar
Fan, Y, Tang, C.Y.. (2013). Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society: Series B: Statistical Methodology, 7, 531–552.CrossRefGoogle Scholar
Friedman, J, Hastie, T, Höfling, H, Tibshirani, R. (2007). Pathwise coordinate optimization. Annals of Applied Statistics, 1 2302–332.CrossRefGoogle Scholar
Friedman, J, Hastie, T, Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33 11.CrossRefGoogle ScholarPubMed
Gorsuch, R. L. (1988). Exploratory factor analysis. In Handbook of multivariate experimental psychology (pp. 231–258). Springer.CrossRefGoogle Scholar
Hendrickson, A.E., White, P.O.. (1966). A method for the rotation of higher-order factors. British Journal of Mathematical and Statistical Psychology, 19 197–103.CrossRefGoogle ScholarPubMed
Henson, R.K., Roberts, J.K.. (2006). Use of exploratory factor analysis in published research: Common errors and some comment on improved practice. Educational and Psychological Measurement, 66 3393–416.CrossRefGoogle Scholar
Hoffman, M.D., Blei, D.M., Wang, C, Paisley, J. (2013). Stochastic variational inference. The Journal of Machine Learning Research, 14 11303–1347.Google Scholar
Horn, J.L.. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30 2179–185.CrossRefGoogle ScholarPubMed
Jennrich, R.I.. (2004). Rotation to simple loadings using component loss functions: The orthogonal case. Psychometrika, 69 2257–273.CrossRefGoogle Scholar
Jennrich, R.I.. (2006). Rotation to simple loadings using component loss functions: The oblique case. Psychometrika, 71 1173–191.CrossRefGoogle Scholar
Jordan, M.I., Ghahramani, Z, Jaakkola, T.S., Saul, L.K.. (1999). An introduction to variational methods for graphical models. Machine Learning, 37 2183–233.CrossRefGoogle Scholar
Kaiser, H.F.. (1958). The varimax criterion for analytic rotation in factor analysis. Psychometrika, 23 3187–200.CrossRefGoogle Scholar
Kupermintz, H, Snow, R.E.. (1997). Enhancing the validity and usefulness of large-scale educational assessments: III NELS: 8.8 mathematics achievement to 12th grade. American Educational Research Journal, 34 1124–150.Google Scholar
Liu, H, Yao, T, Li, R. (2016). Global solutions to folded concave penalized nonconvex learning. Annals of Statistics, 44 2629.CrossRefGoogle ScholarPubMed
McCulloch, C.E.. (1997). Maximum likelihood algorithms for generalized linear mixed models. Journal of the American Statistical Association, 92 437162–170.CrossRefGoogle Scholar
Nishii, R. (1984). Asymptotic properties of criteria for selection of variables in multiple regression. The Annals of Statistics, 2, 758–765.Google Scholar
Nussbaum, E.M., Hamilton, L.S., Snow, R.E.. (1997). Enhancing the validity and usefulness of large-scale educational assessments: IV NELS: 88 science achievement to 12th grade. American Educational Research Journal, 34 1151–173.Google Scholar
Patz, R.J., Junker, B.W.. (1999). A straightforward approach to Markov chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics, 24 2146–178.CrossRefGoogle Scholar
Pinheiro, J.C., Bates, D.M.. (1995). Approximations to the log-likelihood function in the nonlinear mixed-effects model. Journal of Computational and Graphical Statistics, 4 112–35.CrossRefGoogle Scholar
Rabe-Hesketh, S, Skrondal, A, Pickles, A. (2005). Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. Journal of Econometrics, 128 2301–323.CrossRefGoogle Scholar
Reckase, M. D. (2009). Multidimensional item response theory (Vol. 150). Springer.CrossRefGoogle Scholar
Rock, D. A., Pollack, J. M., Owings, J., & Hafner, A. (1991). Psychometric report for the NELS: 88 base year test battery. National Center for Education Statistics.Google Scholar
Shen, X, Pan, W, Zhu, Y. (2012). Likelihood-based selection and sharp parameter estimation. Journal of the American Statistical Association, 107 497223–232.CrossRefGoogle ScholarPubMed
Sun, J, Chen, Y, Liu, J, Ying, Z, Xin, T. (2016). Latent variable selection for multidimensional item response theory models via L1\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$L_1$$\end{document} regularization. Psychometrika, 81 4921–939.CrossRefGoogle Scholar
Takane, Y, De Leeuw, J. (1987). On the relationship between item response theory and factor analysis of discretized variables. Psychometrika, 52 3393–408.CrossRefGoogle Scholar
Thissen, D, Wainer, H. (1982). Some standard errors in item response theory. Psychometrika, 2, 47397–412.Google Scholar
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58 1267–288.CrossRefGoogle Scholar
Tierney, L, Kadane, J.B.. (1986). Accurate approximations for posterior moments and marginal densities. Journal of the American Statistical Association, 81 39382–86.CrossRefGoogle Scholar
von Davier, M, Sinharay, S. (2010). Stochastic approximation methods for latent regression item response models. Journal of Educational and Behavioral Statistics, 35 2174–193.CrossRefGoogle Scholar
von Davier, M. (2009). Is there need for the 3PL model? Guess what?. Measurement: Interdisciplinary Research and Perspectives., 7 2110–114.Google Scholar
Wang, C, Nydick, S.W.. (2015). Comparing two algorithms for calibrating the restricted non-compensatory multidimensional irt model. Applied Psychological Measurement, 39 2119–134.CrossRefGoogle ScholarPubMed
Wang, C, Xu, G. (2015). A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology, 68 3456–477.CrossRefGoogle ScholarPubMed
Wang, T, Xu, P.R., Zhu, L.X.. (2012). Non-convex penalized estimation in high-dimensional models with single-index structure. Journal of Multivariate Analysis, 3, 109221–235.Google Scholar
Wirth, R, Edwards, M.C.. (2007). Item factor analysis: Current approaches and future directions. Psychological Methods, 12 158.CrossRefGoogle ScholarPubMed
Xu, G, Shang, Z. (2018). Identifying latent structures in restricted latent class models. Journal of the American Statistical Association, 113 5231284–1295.CrossRefGoogle Scholar
Yen, M. (1987). A comparison of the efficiency and accuracy of BILOG and LOGIST. Psychometrika, 4, 52275–291.Google Scholar
Zhang, C.H.. (2010). Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics, 38 2894–942.CrossRefGoogle Scholar
Zhang, H, Chen, Y, Li, X. (2020). A note on exploratory item factor analysis by singular value decomposition. Psychometrika, 5, 85358–372.Google Scholar
Zhang, S, Chen, Y, Liu, Y. (2020). An improved stochastic EM algorithm for large-scale full-information item factor analysis. British Journal of Mathematical and Statistical Psychology, 73 144–71.CrossRefGoogle ScholarPubMed
Zou, H. (2006). The adaptive LASSO and its oracle properties. Journal of the American Statistical Association, 7, 1011418–1429.Google Scholar