Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-24T10:43:36.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Going Deep in Diagnostic Modeling: Deep Cognitive Diagnostic Models (DeepCDMs)

Published online by Cambridge University Press:  01 January 2025

Yuqi Gu Open the ORCID record for Yuqi Gu [Opens in a new window]
Yuqi Gu*
Affiliation:
Columbia University
*
Correspondence should be made to Yuqi Gu, Department of Statistics, Columbia University, Room 928 SSW, 1255 Amsterdam Avenue, New York, NY10027, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Cognitive diagnostic models (CDMs) are discrete latent variable models popular in educational and psychological measurement. In this work, motivated by the advantages of deep generative modeling and by identifiability considerations, we propose a new family of DeepCDMs, to hunt for deep discrete diagnostic information. The new class of models enjoys nice properties of identifiability, parsimony, and interpretability. Mathematically, DeepCDMs are entirely identifiable, including even fully exploratory settings and allowing to uniquely identify the parameters and discrete loading structures (the “Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}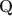-matrices”) at all different depths in the generative model. Statistically, DeepCDMs are parsimonious, because they can use a relatively small number of parameters to expressively model data thanks to the depth. Practically, DeepCDMs are interpretable, because the shrinking-ladder-shaped deep architecture can capture cognitive concepts and provide multi-granularity skill diagnoses from coarse to fine grained and from high level to detailed. For identifiability, we establish transparent identifiability conditions for various DeepCDMs. Our conditions impose intuitive constraints on the structures of the multiple Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}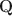-matrices and inspire a generative graph with increasingly smaller latent layers when going deeper. For estimation and computation, we focus on the confirmatory setting with known Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}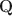-matrices and develop Bayesian formulations and efficient Gibbs sampling algorithms. Simulation studies and an application to the TIMSS 2019 math assessment data demonstrate the usefulness of the proposed methodology.

Keywords

Bayesian inferenceBayesian networkcognitive diagnostic modelDeepCDMdeep generative modeldeep learningdirected graphical modelidentifiabilityQ-matrix
Type
Theory and Methods
Information
Psychometrika , Volume 89 , Issue 1 , March 2024 , pp. 118 - 150
Copyright
Copyright © 2023 The Author(s), under exclusive licence to The Psychometric Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allman, E.S., Matias, C, Rhodes, J.A.. (2009). Identifiability of parameters in latent structure models with many observed variables. The Annals of Statistics, 37 6A3099–3132.CrossRefGoogle Scholar
Almond, R.G., Mislevy, R.J., Steinberg, L.S., Yan, D, Williamson, D.M.Bayesian networks in educational assessment 2015 Springer.CrossRefGoogle Scholar
Balamuta, J.J., Culpepper, S.A.. (2022). Exploratory restricted latent class models with monotonicity requirements under PÒLYA-GAMMA data augmentation. Psychometrika, 87, 903–945.CrossRefGoogle ScholarPubMed
Bengio, Y, Courville, A, Vincent, P. (2013). Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35 81798–1828.CrossRefGoogle ScholarPubMed
Brookhart, S. M. (2010). How to assess higher-order thinking skills in your classroom. ASCD.Google Scholar
Chen, J, de la Torre, J. (2013). A general cognitive diagnosis model for expert-defined polytomous attributes. Applied Psychological Measurement, 37 6419–437.CrossRefGoogle Scholar
Chen, J, de la Torre, J. (2014). A procedure for diagnostically modeling extant large-scale assessment data: The case of the programme for international student aassessment in reading. Psychology, 5 181967.CrossRefGoogle Scholar
Chen, Y, Culpepper, S.A., Chen, Y, Douglas, J. (2018). Bayesian estimation of the DINA Q matrix. Psychometrika, 83 189–108.CrossRefGoogle ScholarPubMed
Chen, Y, Culpepper, S.A., Liang, F. (2020). A sparse latent class model for cognitive diagnosis. Psychometrika, 85 1121–153.CrossRefGoogle ScholarPubMed
Chen, Y, Liu, J, Xu, G, Ying, Z. (2015). Statistical analysis of Q-matrix based diagnostic classification models. Journal of the American Statistical Association, 110 510850–866.CrossRefGoogle Scholar
Chen, Y, Liu, Y, Culpepper, S.A., Chen, Y. (2021). Inferring the number of attributes for the exploratory DINA model. Psychometrika, 86 130–64.CrossRefGoogle ScholarPubMed
Culpepper, S.A.. (2015). Bayesian estimation of the DINA model with Gibbs sampling. Journal of Educational and Behavioral Statistics, 40 5454–476.CrossRefGoogle Scholar
Culpepper, S.A.. (2019). Estimating the cognitive diagnosis Q matrix with expert knowledge: Application to the fraction-subtraction dataset. Psychometrika, 84 2333–357.CrossRefGoogle Scholar
Culpepper, S.A.. (2019). An exploratory diagnostic model for ordinal responses with binary attributes: identifiability and estimation. Psychometrika, 84 4921–940.CrossRefGoogle ScholarPubMed
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76, 179–199.CrossRefGoogle Scholar
de la Torre, J, Douglas, J.A.. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69 3333–353.CrossRefGoogle Scholar
DiBello, L. V., Stout, W. F., & Roussos, L. A. (1995). Unified cognitive/psychometric diagnostic assessment likelihood-based classification techniques. In Cognitively diagnostic assessment, pp. 361389.Google Scholar
Fang, G, Liu, J, Ying, Z. (2019). On the identifiability of diagnostic classification models. Psychometrika, 84 119–40.CrossRefGoogle Scholar
Fishbein, B., Foy, P., & Yin, L. (2021). TIMSS 2019 User guide for the international database (2nd ed.). Retrieved from Boston College, TIMSS & PIRLS International Study Center website: https://timssandpirls.bc.edu/timss2019/international-database/.Google Scholar
Gao, X, Ma, W, Wang, D, Cai, Y, Tu, D. (2021). A class of cognitive diagnosis models for polytomous data. Journal of Educational and Behavioral Statistics, 46 3297–322.CrossRefGoogle Scholar
George, A.C., Robitzsch, A. (2015). Cognitive diagnosis models in R: A didactic. The Quantitative Methods for Psychology, 11 3189–205.CrossRefGoogle Scholar
Gierl, M.J., Leighton, J.P., Hunka, S.M.. (2007). Using the attribute hierarchy method to make diagnostic inferences about respondents’ cognitive skills. In Cambridge, U.K. (Ed.), Cognitive diagnostic assessment for education: Theory and applications, Cambridge University Press 242–274.CrossRefGoogle Scholar
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.Google Scholar
Goodman, L.A.. (1974). Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika, 61 2215–231.CrossRefGoogle Scholar
Gu, Y, Dunson, D.B.. (2023). Bayesian pyramids: Identifiable multilayer discrete latent structure models for discrete data. Journal of the Royal Statistical Society Series B: Statistical Methodology, 85 2399–426.CrossRefGoogle Scholar
Gu, Y, Xu, G. (2019). The sufficient and necessary condition for the identifiability and estimability of the DINA model. Psychometrika, 84 2468–483.CrossRefGoogle ScholarPubMed
Gu, Y, Xu, G. (2020). Partial identifiability of restricted latent class models. Annals of Statistics, 48 42082–2107.CrossRefGoogle Scholar
Gu, Y, Xu, GSufficient and necessary conditions for the identifiability of the Q\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$Q$$\end{document}-matrix Statistica Sinica 2021 31, 449–472.Google Scholar
Gu, Y., & Xu, G. (2022). Identifiability of hierarchical latent attribute models. Statistica Sinica.Google Scholar
Gu, Y, Xu, G. (2023). A joint MLE approach to large-scale structured latent attribute analysis. Journal of the American Statistical Association, 118 541746–760.CrossRefGoogle ScholarPubMed
Hayakawa, S.I.Language in action 1947 Harcourt.Google Scholar
Henson, R.A., Templin, J.L., Willse, J.T.. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika, 74, 191–210.CrossRefGoogle Scholar
Hinton, G.E., Osindero, S, Teh, Y-W. (2006). A fast learning algorithm for deep belief nets. Neural computation, 18 71527–1554.CrossRefGoogle ScholarPubMed
Junker, B.W., Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25, 258–272.CrossRefGoogle Scholar
Koller, D., & Friedman, N. (2009). Probabilistic graphical models: Principles and techniques. MIT press.Google Scholar
Liu, C-W, Andersson, B, Skrondal, A. (2020). A constrained Metropolis-Hastings Robbins-Monro algorithm for Q matrix estimation in DINA models. Psychometrika, 85 2322–357.CrossRefGoogle ScholarPubMed
Ma, W, de la Torre, J. (2020). GDINA: An R package for cognitive diagnosis modeling. Journal of Statistical Software, 93, 1–26.CrossRefGoogle Scholar
Maris, E. (1999). Estimating multiple classification latent class models. Psychometrika, 64 2187–212.CrossRefGoogle Scholar
Morris, T.P., White, I.R., Crowther, M.J.. (2019). Using simulation studies to evaluate statistical methods. Statistics in Medicine, 38 112074–2102.CrossRefGoogle ScholarPubMed
Mourad, R, Sinoquet, C, Zhang, N.L., Liu, T, Leray, P. (2013). A survey on latent tree models and applications. Journal of Artificial Intelligence Research, 47, 157–203.CrossRefGoogle Scholar
Munson, B, Edwards, J, Beckman, M.E., Cohn, A.C., Fougeron, C, Huffman, M.K.. (2011). Phonological representations in language acquisition: Climbing the ladder of abstraction. In Cohn, A.C., Fougeron, C, Huffman, M.K. (Ed.), The Oxford handbook of laboratory phonology, Oxford University Press 288–309.Google Scholar
Pearl, JProbabilistic reasoning in intelligent systems: networks of plausible inference 1988 Morgan Kaufmann.Google Scholar
Polson, N.G., Scott, J.G., Windle, J. (2013). Bayesian inference for logistic models using Pólya-Gamma latent variables. Journal of the American Statistical Association, 108 5041339–1349.CrossRefGoogle Scholar
Ranganath, R, Tang, L, Charlin, L, Blei, D Gale, W.A.. (2015). Deep exponential families. Artificial intelligence and statistics, PMLR 762–771.Google Scholar
Rupp, A.A., Templin, J, Henson, R.A.Diagnostic measurement: theory, methods, and applications 2010 Guilford Press.Google Scholar
Salakhutdinov, R., & Larochelle, H. (2010). Efficient learning of deep Boltzmann machines. In Proceedings of the thirteenth international conference on artificial intelligence and statistics (pp. 693–700). JMLR Workshop and Conference Proceedings.Google Scholar
Schmid, J, Leiman, J.M.. (1957). The development of hierarchical factor solutions. Psychometrika, 22 153–61.CrossRefGoogle Scholar
Schraw, G., & Robinson, D. H. (2011). Assessment of higher order thinking skills. IAP.Google Scholar
Tatsuoka, K.K.. (1983). Rule space: An approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 20, 345–354.CrossRefGoogle Scholar
Templin, J, Bradshaw, L. (2014). Hierarchical diagnostic classification models: A family of models for estimating and testing attribute hierarchies. Psychometrika, 79 2317–339.CrossRefGoogle ScholarPubMed
Templin, J.L., Henson, R.A.. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychological Methods, 11 3287.CrossRefGoogle ScholarPubMed
Templin, J.L., Henson, R.A., Templin, S.E., Roussos, L. (2008). Robustness of hierarchical modeling of skill association in cognitive diagnosis models. Applied Psychological Measurement, 32 7559–574.CrossRefGoogle Scholar
von Davier, M. (2008). A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology, 61, 287–307.CrossRefGoogle ScholarPubMed
von Davier, M., & Lee, Y.-S. (2019). Handbook of diagnostic classification models. Springer International Publishing.CrossRefGoogle Scholar
Wainwright, M. J., & Jordan, M. I. (2008). Graphical models, exponential families, and variational inference. Foundations and Trends® in Machine Learning, 1(1–2):1–305.Google Scholar
Xu, G. (2017). Identifiability of restricted latent class models with binary responses. Annals of Statistics, 45, 675–707.CrossRefGoogle Scholar
Xu, G, Shang, Z. (2018). Identifying latent structures in restricted latent class models. Journal of the American Statistical Association, 113 5231284–1295.CrossRefGoogle Scholar
Xu, G, Zhang, S. (2016). Identifiability of diagnostic classification models. Psychometrika, 81 3625–649.CrossRefGoogle ScholarPubMed
Xu, X, von Davier, M. (2008). Fitting the structured general diagnostic model to NAEP data. ETS Research Report Series, 2008 1i–18.CrossRefGoogle Scholar
Yung, Y-F, Thissen, D, McLeod, L.D.. (1999). On the relationship between the higher-order factor model and the hierarchical factor model. Psychometrika, 64, 113–128.CrossRefGoogle Scholar
Supplementary material: File

Gu supplementary material

Gu supplementary material
Download Gu supplementary material(File)
File 219.4 KB