Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-22T04:36:35.536Z Has data issue: false hasContentIssue false
  • English
  • Français

Empirical Bayes Estimates of Domain Scores Under Binomial and Hypergeometric Distributions for Test Scores

Published online by Cambridge University Press:  01 January 2025

Miao-Hsiang Lin  and
Chao A. Hsiung
Miao-Hsiang Lin*
Affiliation:
Institute of Statistical Science, Academia Sinica
Chao A. Hsiung
Affiliation:
Institute of Statistical Science, Academia Sinica
*
Requests for reprints should be sent to Miao-Hsiang Lin, Institute of Statistical Science, Academia Sinica, Taipei, 11529, Taiwan, R.O.C.
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce two simple empirical approximate Bayes estimators (EABEs)— \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}_N (x)$$\end{document}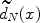 and \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta _N (x)$$\end{document}—for estimating domain scores under binomial and hypergeometric distributions, respectively. Both EABEs (derived from corresponding marginal distributions of observed test score x without relying on knowledge of prior domain score distributions) have been proven to hold Δ-asymptotic optimality in Robbins' sense of convergence in mean. We found that, where \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}^* _N$$\end{document}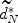 and \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta ^* _N$$\end{document} 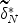are the monotonized versions of \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}_N$$\end{document} 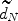and \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta _N$$\end{document} 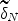under Van Houwelingen's monotonization method, respectively, the convergence rate of the overall expected loss of Bayes risk in either \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}^* _N$$\end{document} 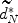or \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta ^* _N$$\end{document} 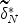depends on test length, sample size, and ratio of test length to size of domain items. In terms of conditional Bayes risk, \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}^* _N$$\end{document} and \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta ^* _N$$\end{document}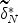 outperform their maximum likelihood counterparts over the middle range of domain scales. In terms of mean-squared error, we also found that: (a) given a unimodal prior distribution of domain scores, \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta ^* _N$$\end{document} 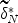performs better than both \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}^* _N$$\end{document} and a linear EBE of the beta-binomial model when domain item size is small or when test items reflect a high degree of heterogeneity; (b) \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde{d}^* _N$$\end{document}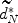 performs as well as \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\widetilde\delta ^* _N$$\end{document} 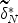when prior distribution is bimodal and test items are homogeneous; and (c) the linear EBE is extremely robust when a large pool of homogeneous items plus a unimodal prior distribution exists.

Keywords

Bayes riskΔ-asymptotic optimalitybinomial and hypergeometric modelsprior-hyperprior approachsimple empirical Bayes estimateVan Houwelingen's monotonization method
Type
Original Paper
Information
Psychometrika , Volume 59 , Issue 3 , September 1994 , pp. 331 - 359
Copyright
Copyright © 1994 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are indebted to both anonymous reviewers, especially Reviewer 2, and the Editor for their invaluable comments and suggestions. Thanks are also due to Yuan-Chin Chang and Chin-Fu Hsiao for their help with our simulation and programming work.

References

American Psychological Association, American Educational Research Association, & National Council on Measurement in Education. (1985). Standards for educational and psychological tests, Washington, DC: American Psychological Association.Google Scholar
Berk, R. (1980). A consumer's guide to criterion-referenced test reliability. Journal of Educational Measurement, 17, 323–349.CrossRefGoogle Scholar
Chung, K. L. (1974). A course in probability theory, New York: Academic Press.Google Scholar
Cressie, N. (1982). A useful empirical Bayes identity. The Annals of Statistics, 10, 625–629.CrossRefGoogle Scholar
Cressie, N., Seheult, A. (1985). Empirical Bayes estimation in sampling inspection. Biometrika, 72, 451–458.CrossRefGoogle Scholar
Deely, J. J., Lindley, D. V. (1981). Bayes Empirical Bayes. Journal of the American Statistical Association, 76, 833–841.CrossRefGoogle Scholar
Johnson, N., Kotz, S. (1969). Discrete distribution in statistics: Distributions, New York: Wiley.Google Scholar
Keats, J. A., Lord, F. M. (1962). A theoretical distribution for mental test scores. Psychometrika, 27, 59–72.CrossRefGoogle Scholar
Lin, M. H., Hsiung, C. A., Hsiao, C. F. (1994). A computing program for monotonizing two empirical Bayes estimators in binomial and hypergeometric data distributions. Psychometrika, 59, 423–424.CrossRefGoogle Scholar
Lord, F. M., Novick, M. R. (1968). Statistical theories of mental test scores, Reading, MA: Addison-Wesley.Google Scholar
Maritz, J. S., Lwin, T. (1975). Construction of simple empirical Bayes estimators. Journal of the Royal Statistical Society, Series B, 39, 421–425.CrossRefGoogle Scholar
Maritz, J., Lwin, J. (1989). Empirical Bayes methods, London: Chapman and Hall.Google Scholar
Meredith, W., Kearns, J. (1973). Empirical Bayes point estimates of latent trait scores without knowledge of the trait distribution. Psychometrika, 38, 533–554.CrossRefGoogle Scholar
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 105(1), 156–166.CrossRefGoogle Scholar
Millman, J. (1974). Criterion referenced measurement. In Popham, W. J. (Eds.), Evaluation in education: Current application, Berkeley, CA: McCutcheon.Google Scholar
Mood, A., Graybill, F., Boes, D. (1974). Introduction to the theory of statistics, New York: McGraw-Hill.Google Scholar
Nichols, W. G., Tsokos, C. P. (1972). Empirical Bayes point estimation in a family of probability distributions. International Statistical Review, 40, 147–151.CrossRefGoogle Scholar
Popham, W. J. (1984). Specifying the domain of content or behaviors. In Berk, R. A. (Eds.), A guide to criterion-referenced test construction (pp. 29–48). Baltimore: Johns Hopkins University Press.Google Scholar
Robbins, H. (1964). The empirical Bayes approach to statistical decision problems. Annals Mathematical Statistics, 35, 1–20.CrossRefGoogle Scholar
Rutherford, J. R., Krutchkoff, R. G. (1969). Some empirical Bayes techniques in point estimation. Biometrika, 56, 133–137.CrossRefGoogle Scholar
van der Linden, W. J. (1979). Binomial test models and item difficulty. Applied Psychological Measurement, 3, 401–411.CrossRefGoogle Scholar
Van Houwelingen, J. C. (1977). Monotonizing empirical Bayes estimators for a class of discrete distributions with monotone likelihood ratio. Statistica Neerlandica, 31, 95–104.CrossRefGoogle Scholar
Wilcox, R. R. (1979). A lower bound to the probability of choosing the optimal passing scores for a mastery test when there is an external criterion. Psychometrika, 44, 245–249.CrossRefGoogle Scholar