Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-03T05:35:13.416Z Has data issue: false hasContentIssue false
  • English
  • Français

How to Commit the Gambler's Fallacy and Get Away with It

Published online by Cambridge University Press:  28 February 2022

Davis Baird  and
Richard E. Otte
Davis Baird
Affiliation:
University of Arizona
Richard E. Otte
Affiliation:
University of Arizona and University of Pittsburgh
Get access Rights & Permissions [Opens in a new window]

Extract

The gambler's fallacy runs like this: We know

  • 1) the bias for heads of a certain coin and flipping device is 1/2, and

  • 2) flips of the coin with the flipping device are independent.

Given these facts we can easily compute the probability of 4 heads or fewer turning up in 20 flips, P(h≤4), to be

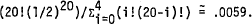
Suppose we flip the coin 15 times and get—improbably enough—all tails. If the coin lands tails up once more in the next 5 flips the improbable event of 4 or fewer heads in 20 flips, h≤4, will have occurred. Since P(h≤4) is so small we might be tempted to infer that all of the next five flips will be heads.

Type
Part IV. Probability and Statistical Inference
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1982 , Issue 1: Volume One: Contributed Papers 1982 , 1982 , pp. 169 - 180
Copyright
Copyright © Philosophy of Science Association 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baird, D. (1981). Significance Tests; Their Logic and Early History. Unpublished Ph.D. Dissertation, Stanford University.Google Scholar
Carnap, R. (1947). “On the Application of Inductive Logic.” Philosophy and Phenomenological Research 8: 133—148.CrossRefGoogle Scholar
Cox, D.R. and Hinkley, D.V. (1974). Theoretical Statistics . London: Chapman and Hall Ltd.CrossRefGoogle Scholar
Fisher, R.A. (1956). Statistical Methods and Scientific Inference. New York: Hafner Publishing Company.Google Scholar
Fisher, R.A. (1970). Statistical Methods for Research Workers. 14th ed. New York: Hafner Publishing Company.Google Scholar
Hacking, Ian. (1965). Logic of Statistical Inference. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Hacking, Ian. (1980). “Grounding Probabilities from Below.” In PSA 1980, Volume 1. Edited by Asquith, P.D. and Giere, R.N.. East Lansing, Michigan: Philosophy of Science Association. Pages 110–116.Google Scholar
Neyman, J. (1952). First Course in Probability and Statistics. New York: H. Holt and Company.Google Scholar
Russell, B. (1935). Religion and Science. London: T. Butterworth.Google Scholar
Salmon, W. (1971). Statistical Explanation and Statistical Relevance. Pittsburgh: University of Pittsburgh Press.CrossRefGoogle Scholar
Seidenfeld, T. (1979). Philosophical Problems of Statistical Inference: Learning from R.A. Fisher. Dordrecht: Reidel.Google Scholar