Introduction
The Hermitian system, in view of its energy conservation property and guaranteed real eigenvalues, plays a key role in both quantum physics and classical wave systems. However, the inevitable coupling with the external environment generally produces energy exchange and leads to energy gain/loss (Bender et al., Reference Bender, Brody and Jones2003; Bender, Reference Bender2007), which results in the breakdown of Hermiticity, thus requiring a non-Hermitian description. In recent decades, a flourishing development of non-Hermitian manipulation in open systems has been witnessed. It has been shown that non-Hermiticity not only offers suitable physical descriptions to non-conservative systems but also generates more unprecedented and exotic physics. In particular, with chiastopic fusion with another frontier field of metamaterials, non-Hermitian meta-structures have attracted ever-increasing attention and brought new perspectives to engineer architected structures with extraordinary wave-manipulation capabilities.
In a non-Hermitian system, gain/loss is treated as an imaginary part of the eigenvalue, which results in the eigenvalue ceasing to be complex. However, a unique case, known as a parity-time-symmetric (PT-symmetric) system (Hou and Assouar, Reference Hou and Assouar2018; Qi et al., Reference Qi, Chen, Ge, Berini and Ma2019; Fang et al., Reference Fang, Gerard, Zhou, Ding, Wang, Jia and Li2021a; Cao et al., Reference Cao, Zhu, Wan, Zeng and Assouar2022; Yi et al., Reference Yi, Li, Negahban, Xia and Zhu2022), with balanced gain and loss can possess real eigenvalues in non-Hermitian condition. In a PT-symmetric system, the exceptional point (EP) is a concept that cannot be ignored. The real and imaginary parts of eigenvalues coalesce at this critical value, and numerous particular phenomena may arise around the EP (Ding et al., Reference Ding, Ma, Xiao, Zhang and Chan2016; Rosa et al., Reference Rosa, Mazzotti and Ruzzene2021). For example, let us direct our attention towards a scenario involving two resonators interconnected by a slender tube (Gao et al., Reference Gao, Xue, Wang, Gu, Liu, Zhu and Zhang2020; Gu et al., Reference Gu, Gao, Cao, Liu, Zhu and Zhu2021). The introduction of gain or loss within one or both resonators leads us into the realm of the non-Hermitian regime. Within this context of non-Hermitian manipulation, the system has the potential to traverse an EP, a juncture that interconnects the phases of PT symmetry and PT breaking. This progression is distinctly observable through the dynamic changes experienced by both the real and imaginary components of the eigenfrequency. Concomitant with the alterations in the non-Hermitian modulation, a phenomenon known as non-Hermitian degeneracy emerges. This effect becomes particularly apparent when scrutinizing the developmental trajectory of the eigenfrequency driven by the introduction of non-Hermiticity (Gao et al., Reference Gao, Xue, Wang, Gu, Liu, Zhu and Zhang2020; Gu et al., Reference Gu, Gao, Cao, Liu, Zhu and Zhu2021):
Herein,
![]() ${a}_1$
and
${a}_1$
and
![]() ${a}_2$
indicate the amplitudes of the field within the two resonators,
${a}_2$
indicate the amplitudes of the field within the two resonators,
![]() $\kappa$
is the strength of reciprocal coupling,
$\kappa$
is the strength of reciprocal coupling,
![]() ${\omega}_1$
and
${\omega}_1$
and
![]() ${\omega}_2$
are the resonant frequencies of the two resonators, and
${\omega}_2$
are the resonant frequencies of the two resonators, and
![]() ${\gamma}_1$
and
${\gamma}_1$
and
![]() ${\gamma}_2$
indicate non-Hermitian modulation, respectively. The aforementioned developments can be succinctly elucidated through the application of coupled-mode theory (Maksimov et al., Reference Maksimov, Sadreev, Lyapina and Pilipchuk2015; Huang et al., Reference Huang, Liu, Zhou, Wang, Zhu and Li2020). Given a time-dependence of the form
${\gamma}_2$
indicate non-Hermitian modulation, respectively. The aforementioned developments can be succinctly elucidated through the application of coupled-mode theory (Maksimov et al., Reference Maksimov, Sadreev, Lyapina and Pilipchuk2015; Huang et al., Reference Huang, Liu, Zhou, Wang, Zhu and Li2020). Given a time-dependence of the form
![]() ${e}^{i\omega t,}$
, an expression for the eigenfrequency of the interconnected cavities can be obtained as
${e}^{i\omega t,}$
, an expression for the eigenfrequency of the interconnected cavities can be obtained as
 $$\begin{align}{\omega}_{\pm}={\omega}_0+i\frac{\gamma_1+{\gamma}_2}{2}\pm \sqrt{\kappa^2-\frac{{\left({\gamma}_1-{\gamma}_2\right)}^2}{4}}\end{align}$$
$$\begin{align}{\omega}_{\pm}={\omega}_0+i\frac{\gamma_1+{\gamma}_2}{2}\pm \sqrt{\kappa^2-\frac{{\left({\gamma}_1-{\gamma}_2\right)}^2}{4}}\end{align}$$
Equation (3) delineates that alterations in the modulation coefficient lead to the attainment of non-Hermitian conditions. It subsequently resulted in the emergence of degeneracy within the eigenfrequency curves, which was influenced by fluctuations in the non-Hermitian coupling strength. Drawing from the foundations laid by Eqs. (1) and (2), we can additionally derive the effective Hamiltonian of the system in a matrix form:
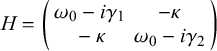 $$\begin{align}H=\left(\begin{array}{cc}{\omega}_0-i{\gamma}_1& -\kappa \\ {}-\kappa & {\omega}_0-i{\gamma}_2\end{array}\right)\end{align}$$
$$\begin{align}H=\left(\begin{array}{cc}{\omega}_0-i{\gamma}_1& -\kappa \\ {}-\kappa & {\omega}_0-i{\gamma}_2\end{array}\right)\end{align}$$
Through the solution of the eigenvalues inherent to this matrix, one can derive the expression for the eigenfrequencies as well. Indeed, the effective Hamiltonian has emerged as a versatile tool, assuming a pivotal role in the exploration of non-Hermitian modulation. As summarized in Figure 1, extraordinary wave phenomena in non-Hermitian meta-structures have received unprecedented attention in the fields of electromagnetic, acoustic, and elastic waves. Perfect absorption (Achilleos et al., Reference Achilleos, Theocharis, Richoux and Pagneux2017) and asymmetric diffraction (Zhong et al., Reference Zhong, Kou, Özdemir and El-Ganainy2020) can be realized by inspiring the appearance of EP. Furthermore, the coupling between wave control and non-Hermiticity can achieve intriguing wave manipulations like wave amplification (Wen et al., Reference Wen, Zhu, Fan, Tam, Zhu, Wu and Li2022), unidirectional transparency (Wu et al., Reference Wu, Chen and Huang2019), and the skin effect (Weidemann et al., Reference Weidemann, Kremer, Helbig, Hofmann, Stegmaier, Greiter and Szameit2020). Meanwhile, the emergence of non-Hermitian wave phenomena has significantly broadened their corresponding applications and shown tremendous functionalities, such as whispering gallery (Hu et al., Reference Hu, Zhang, Zhang, Zheng, Xiong, Yue and Liu2021; Pernas-Salomón et al., Reference Pernas-Salomón, Zheng, Zhang, Gao, Liu, Cheng and Christensen2022), energy harvesting (Cai et al., Reference Cai, Jin, Li, Rabczuk, Pennec, Djafari-Rouhani and Zhuang2022), holographic projection (Zhu et al., Reference Zhu, Hu, Fan, Yang, Liang, Zhu and Cheng2018b), topological structures (Mandal et al., Reference Mandal, Banerjee and Liew2022), acoustic diode (Zhang et al., Reference Zhang, Peng, Özdemir, Liu, Jing, Lü and Nori2015), single-mode laser (Feng et al., Reference Feng, Wong, Ma, Wang and Zhang2014), noise control (Huang et al., Reference Huang, Fang, Wang, Assouar, Cheng and Li2018), and tunable filter (Puri et al., Reference Puri, Ferdous, Shakeri, Basiri, Dubois and Ramezani2021).
Figure 1. Non-Hermitian physical phenomena and applications (Feng et al., Reference Feng, Wong, Ma, Wang and Zhang2014; Zhang et al., Reference Zhang, Peng, Özdemir, Liu, Jing, Lü and Nori2015; Fleury et al., Reference Fleury, Sounas and Alù2015b; Achilleos et al., Reference Achilleos, Theocharis, Richoux and Pagneux2017; Huang et al., Reference Huang, Fang, Wang, Assouar, Cheng and Li2018; Zhu et al., Reference Zhu, Hu, Fan, Yang, Liang, Zhu and Cheng2018b; Qi et al., Reference Qi, Chen, Ge, Berini and Ma2019; Wu et al., Reference Wu, Chen and Huang2019; Weidemann et al., Reference Weidemann, Kremer, Helbig, Hofmann, Stegmaier, Greiter and Szameit2020; Zhong et al., Reference Zhong, Kou, Özdemir and El-Ganainy2020; Fang et al., Reference Fang, Kottos and Thevamaran2021b; Hu et al., Reference Hu, Zhang, Zhang, Zheng, Xiong, Yue and Liu2021; Puri et al., Reference Puri, Ferdous, Shakeri, Basiri, Dubois and Ramezani2021; Cai et al., Reference Cai, Jin, Li, Rabczuk, Pennec, Djafari-Rouhani and Zhuang2022; Mandal et al., Reference Mandal, Banerjee and Liew2022; Pernas-Salomón et al., Reference Pernas-Salomón, Zheng, Zhang, Gao, Liu, Cheng and Christensen2022; Wen et al., Reference Wen, Zhu, Fan, Tam, Zhu, Wu and Li2022).
Early attempts at non-Hermitian wave control can be traced back to electromagnetics. Quite a few non-Hermitian meta-structures have been proposed to manipulate electromagnetic waves by changing the amplitude, phase, and transmission properties (Khorasaninejad et al., Reference Khorasaninejad, Chen, Devlin, Oh, Zhu and Capasso2016). Specifically, the physical properties of electromagnetic meta-structures are mainly delineated by effective permittivity and permeability. When non-Hermitian elements are introduced to electromagnetics, meta-structures can innovatively employ these two vital elements in a complex space and enrich striking applications (Pendry, Reference Pendry2000). For simplicity, we focus on two non-Hermitian features of electromagnetic meta-structures: 1) The appearance of EP (Chen et al., Reference Chen, Liu, Luan, Liu, Wang, Zhu and Gao2020; Dong et al., Reference Dong, Hu, Wang, Jia, Zhang, Cao and Qiu2020; Wang et al., Reference Wang, Jiang, Zhao, Zhang, Hsu, Peng and Yang2020). Figure 2(a) illustrates an electromagnetic metasurface that can realize angular asymmetry at EP. It exhibits completely suppressed reflection when light is incident from the left, whereas highly efficient retro-reflection occurs from the opposite side. The loss is introduced by adding a slit in the subunit and the angle asymmetry is obtained by accurately manipulating the phase gradient and diffraction orders. 2) The combination of PT symmetry and electromagnetics (Feng et al., Reference Feng, Wong, Ma, Wang and Zhang2014; Chen and Jung, Reference Chen and Jung2016; Gu et al., Reference Gu, Bai, Zhang, Jin, Zhang, Zhang and Lee2017). In Figure 2(b), PT symmetry is realized by adjusting the resistive metallic filament and amplifying the graphene metasurface to balance the loss and gain. When THz waves are incident, the coupling between the spectral singularity and the chemical sensitivity of graphene may give rise to unidirectional reflectionlessness.
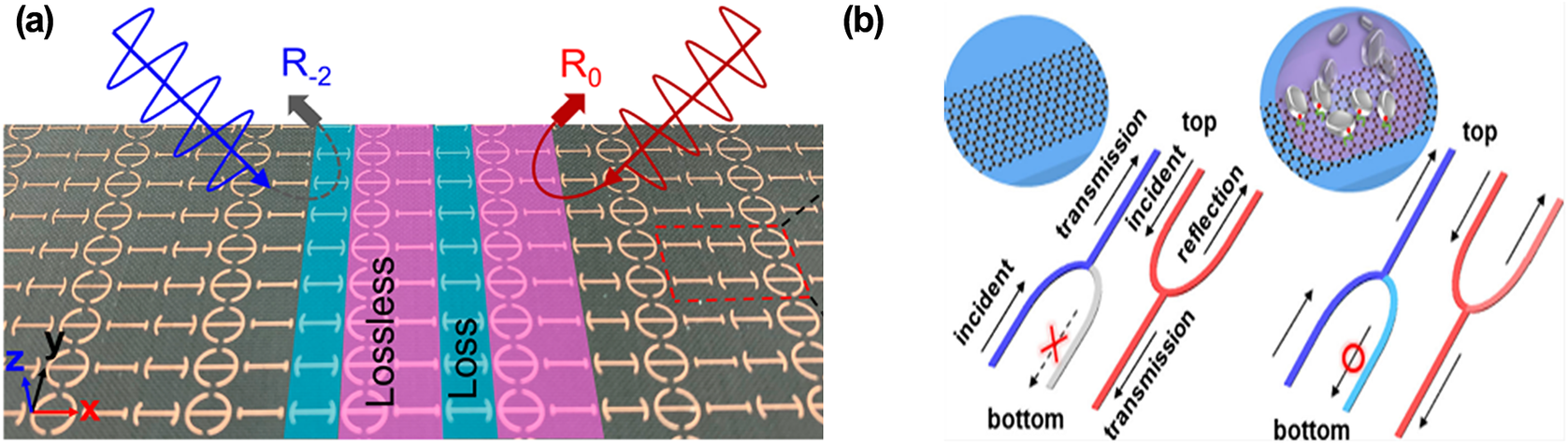
Figure 2. (a) Unidirectional retro-reflection for non-Hermitian metasurface (Dong et al., Reference Dong, Hu, Wang, Jia, Zhang, Cao and Qiu2020). (b) Illustration of the transmission and reflection of THz waves incident from the bottom (outlined as blue) and top (outlined as red) of a PT-symmetric sensor (Chen and Jung, Reference Chen and Jung2016).
In contrast to electromagnetics, acoustics is, to a great extent, treated as a particular platform to pursue potential physical progress. In recent decades, with the dawn of non-Hermitian systems, the coupling between non-Hermitian and acoustic waves has provided a pioneering future in acoustic wave control. Compared to minimizing loss, the performance efficiency of non-Hermitian acoustic meta-structures can be greatly improved by precisely modulating the loss (Achilleos et al., Reference Achilleos, Theocharis, Richoux and Pagneux2017; Hou et al., Reference Hou, Ni and Assouar2018; Zhu and Assouar, Reference Zhu and Assouar2019; Magariyachi et al., Reference Magariyachi, Casals, Herrero, Botey and Staliunas2021). The most notable realizations are the accurate manipulation of diffraction orders (Fang et al., Reference Fang, Gerard, Zhou, Ding, Wang, Jia and Li2021a; Li et al., Reference Li, Shen, Xie, Li, Wang, Cummer and Jing2017; Yang et al., Reference Yang, Jia, Bi, Zhao and Yang2019) and the realization of asymmetric waveguides (Zhang et al., Reference Zhang, Peng, Özdemir, Liu, Jing, Lü and Nori2015; Fleury et al., Reference Fleury, Sounas and Alù2015a; Ramezani et al., Reference Ramezani, Dubois, Wang, Shen and Zhang2016; Shi et al., Reference Shi, Dubois, Chen, Cheng, Ramezani, Wang and Zhang2016; Lee et al., Reference Lee, Nomura, Dede and Iizuka2020; Zheng et al., Reference Zheng, Park, Liu, Zhu, Hu and Kim2020; Ju et al., Reference Ju, Zou, Qian and Liu2021; Li et al., Reference Li, Huang, Cheng and Li2021). We first review the above outstanding phenomena by introducing reflection- and transmission-type metasurfaces. As Figure 3(a) exhibits, Li et al. (Reference Li, Shen, Xie, Li, Wang, Cummer and Jing2017) proposed a lossy acoustic metasurface in 2017. After introducing an isotropic loss in the metasurface unit cells, tunable acoustic asymmetric transmission can be achieved. In 2019, Wang et al. (Reference Wang, Fang, Mao, Jing and Li2019) proposed a gradient index lossy reflection-type metasurface. With an exactly tailored metasurface, extremely asymmetrical reflection was realized at the EP by harnessing the loss. As illustrated in Figure 3(b), the loss changes in the subunit can control the diffraction orders. When the incidence angle
![]() ${\theta}_i={45}^{{}^{\circ}}\!$
, the specular reflection and the extraordinary reflection are strongly suppressed. However, for
${\theta}_i={45}^{{}^{\circ}}\!$
, the specular reflection and the extraordinary reflection are strongly suppressed. However, for
![]() ${\theta}_i=-{45}^{{}^{\circ}}\!$
, only the specular reflection is suppressed. Extraordinary reflection still exists in the form of an extremely asymmetrical reflection.
${\theta}_i=-{45}^{{}^{\circ}}\!$
, only the specular reflection is suppressed. Extraordinary reflection still exists in the form of an extremely asymmetrical reflection.
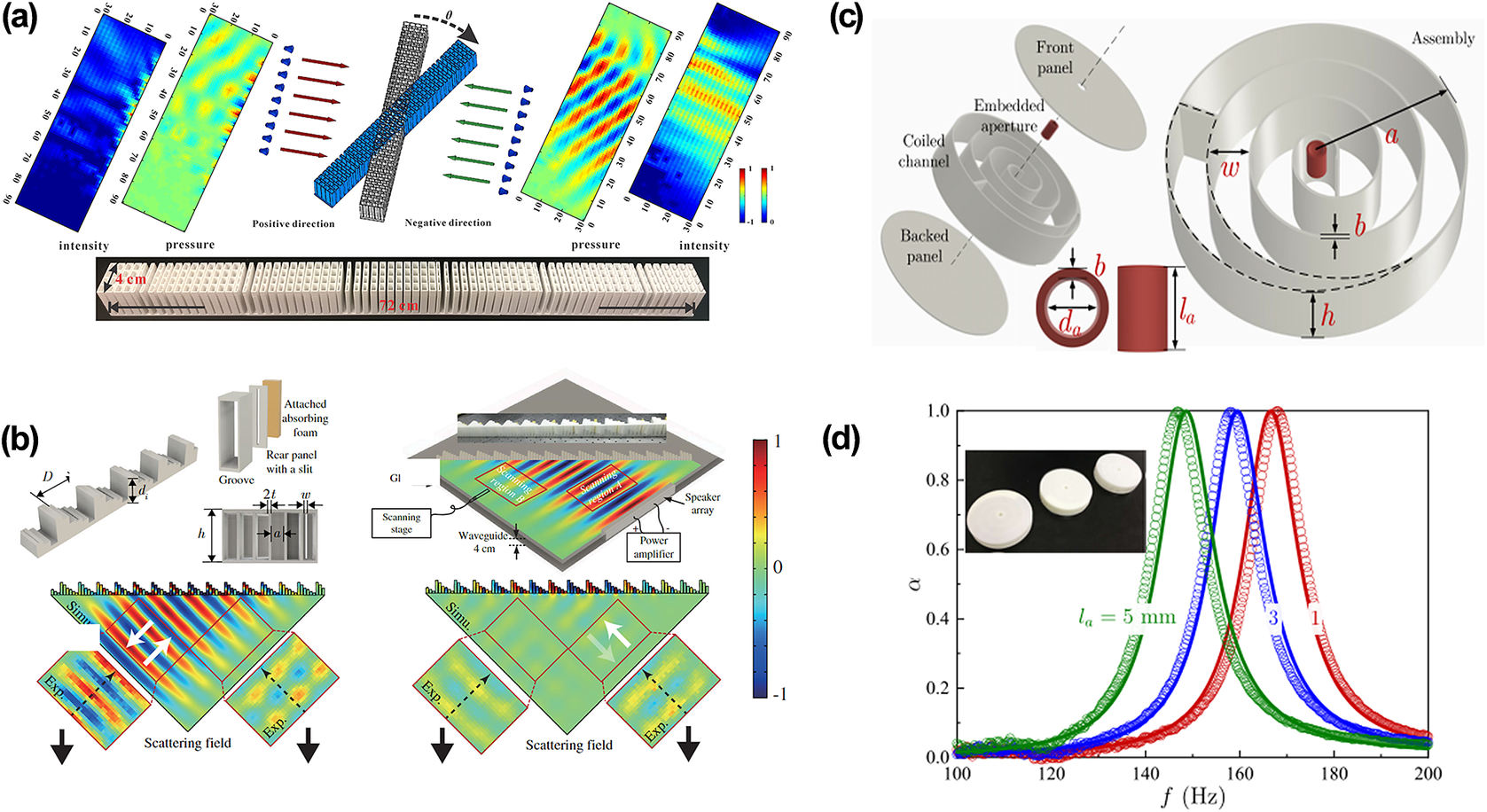
Figure 3. (a) Asymmetric transmission via lossy metasurface (Li et al., Reference Li, Shen, Xie, Li, Wang, Cummer and Jing2017). (b) Gradient index lossy metasurface and asymmetric wave phenomenon (Wang et al., Reference Wang, Fang, Mao, Jing and Li2019). (c) Spiral metasurface (Huang et al., Reference Huang, Fang, Wang, Assouar, Cheng and Li2018). (d) The perfect absorptions when the lengths of embedded apertures are 5 mm, 3 mm, and 1 mm (Hu et al., Reference Hu, Zhang, Zhang, Zheng, Xiong, Yue and Liu2021).
Meanwhile, along with systematic non-Hermitian manipulations that have been introduced into acoustics (Gerard and Jing, Reference Gerard and Jing2020; Gu et al., Reference Gu, Gao, Cao, Liu, Zhu and Zhu2021), non-Hermitian acoustic meta-structures are capable of numerous rich-wave phenomena (Popa et al., Reference Popa, Shinde, Konneker and Cummer2015; Liu et al., Reference Liu, Zhu, Chen, Liang and Zhu2018; Zhu et al., Reference Zhu, Fang, Li, Sun, Li, Jing and Chen2018a; Lan et al., Reference Lan, Zhang, Wang, Lai and Liu2020), including perfect absorption (Achilleos et al., Reference Achilleos, Theocharis, Richoux and Pagneux2017; Huang et al., Reference Huang, Fang, Wang, Assouar, Cheng and Li2018), wave amplification (Poshakinskiy et al., Reference Poshakinskiy, Poddubny and Fainstein2016; Hu et al., Reference Hu, Zhang, Zhang, Zheng, Xiong, Yue and Liu2021), holographic projection (Zhu et al., Reference Zhu, Hu, Fan, Yang, Liang, Zhu and Cheng2018b; Zhu and Assouar, Reference Zhu and Assouar2019), and unidirectionally invisible cloak (Zhu et al., Reference Zhu, Ramezani, Shi, Zhu and Zhang2014). Typically, a perfect acoustic absorber via a spiral metasurface composed of coiled channels and embedded apertures has been proposed (Huang et al., Reference Huang, Fang, Wang, Assouar, Cheng and Li2018) (Figure 3(c)). The embedded aperture offers additional freedom and hence can tune the impedance independently. In Figure 3(d), by modulating the ratio between the resistance and reactance, this structure is able to realize perfect absorption with tunable frequencies. This non-Hermitian design may contribute tremendously to relevant applications in low-frequency acoustic absorption. In addition, by combining acoustic resonances with non-Hermitian ingredients, Hu et al. proposed a triangular crystal made of a topological lattice that can generate the topological whispering gallery (Hu et al., Reference Hu, Zhang, Zhang, Zheng, Xiong, Yue and Liu2021). Here, the topological lattice is realized by adding gain elements, namely pasting carbon nanotubes on the insulator rods. This system breaks the chiral symmetry of the whispering-gallery modes and achieves simplified acoustic waveguides in topologically robust environments. Furthermore, this design may contribute to nondestructive testing and acoustic sensing.
Following the development of non-Hermitian modulation, extensive acoustic and electromagnetic applications of non-Hermitian systems have been introduced in multiple reviews (Wang et al., Reference Wang, Zhang, Hua, Lei, Lu and Chen2021; Ding et al., Reference Ding, Fang and Ma2022; Zhang et al., Reference Zhang, Zhang, Lu and Chen2022; Lin et al., Reference Lin, Tai, Li and Lee2023). Specifically, Nikhil et al. treated the loss as more of a friend than a foe and systematically introduced corresponding applications of non-Hermitian acoustic metasurfaces in 2019 (Gerard and Jing, Reference Gerard and Jing2020). In 2021, Gu et al. analysed the mechanisms of non-Hermitian metasurfaces using basic concepts and mathematical tools (Gu et al., Reference Gu, Gao, Cao, Liu, Zhu and Zhu2021). Apart from acoustics and electromagnetics, elastic waves play a vital role in nontrivial physics and reality. Compared with electromagnetics and acoustics, elastic waves can produce more complex multi-mode coupling, conversion, and dispersion characteristics. Moreover, recent developments in non-Hermitian control have prompted us to see loss and gain in a new light: as ubiquitous elements in environment, precise manipulation of non-Hermiticity can open new avenues for unconventional strategies over elastic-wave control. Due to the fact that few existing reviews trace systematic research into elastic waves with non-Hermiticity, in this perspective, we focus on the coupling between non-Hermitian and elastic waves and summarize the corresponding investigations. The contents of this paper are organized as follows: firstly, we introduce the non-Hermitian system of elastic waves. In particular, we focus on non-Hermitian subwavelength structures including non-Hermitian metamaterials and metasurfaces. Secondly, we discuss the bulk-boundary correspondence (BBC) under the Hermitian condition. Furthermore, by extending the BBC to non-Hermitian systems, we mainly summarize a peculiarly interesting phenomenon, the non-Hermitian skin effect in elastic waves. Finally, we outline the perspectives and challenges of non-Hermitian elastic meta-structures for future key opportunities.
Non-Hermitian in elastodynamics
Non-Hermitian phenomena expand the degrees of freedom of wave manipulations and inspire potential applications in elastic waves (Liu et al., Reference Liu, Zhang, Mao, Zhu, Yang, Chan and Sheng2000; Jung et al., Reference Jung, Kim, Goo, Chang and Wang2019). Therefore, to investigate the internal mechanisms of non-Hermitian elastic systems, we subdivide them into two sections: non-Hermitian elastic metamaterials and non-Hermitian elastic metasurfaces. Recently, accompanied by the rise of non-Hermitian modulation, various applications have been innovatively realized in metamaterials. Thus, to summarize the significant properties of non-Hermitian elastic metamaterials, we first discuss the following three aspects: 1) PT-symmetric metamaterials; 2) inspiring the realization of EP; and 3) topological non-Hermitian metamaterials.
Non-Hermitian elastic metamaterials
Parity-time-symmetric metamaterials
PT-symmetric metamaterials exhibit balanced loss and gain, thus maintaining energy conservation. An attractive phenomenon shows that these structures also possess real eigenvalues and hence exhibit unique physical characteristics (Hou and Assouar, Reference Hou and Assouar2018; Fang et al., Reference Fang, Gerard, Zhou, Ding, Wang, Jia and Li2021a; Cao et al., Reference Cao, Zhu, Wan, Zeng and Assouar2022; Yi et al., Reference Yi, Ma, Xia, Negahban, Chen and Li2022). Active control offers a highly efficient method to designing PT-symmetric elastic metamaterials (Hou et al., Reference Hou, Ni and Assouar2018). As illustrated in Figure 4(a), a PT-symmetric piezoelectric metamaterial was proposed with external circuits containing positive and negative resistances. This tunable device, manipulated by an external shunted circuit, can run at the expected frequency without any geometric change (Hou and Assouar, Reference Hou and Assouar2018). As such, the outstanding tunability of these active control systems provides comprehensive versatility and high performance for non-Hermitian elastic metamaterials. Alternatively, upon further exploration, a periodic-like coherent perfect absorber was demonstrated in a PT-symmetric metamaterial beam (Yi et al., Reference Yi, Li, Negahban, Xia and Zhu2022). As Figure 4(b) illustrates, the loss/gain element is supplied by the positive/negative resistance of an external circuit. It is noteworthy that this particular periodicity can be predicted by observing the related frequency of the maximum Bloch wavenumber.
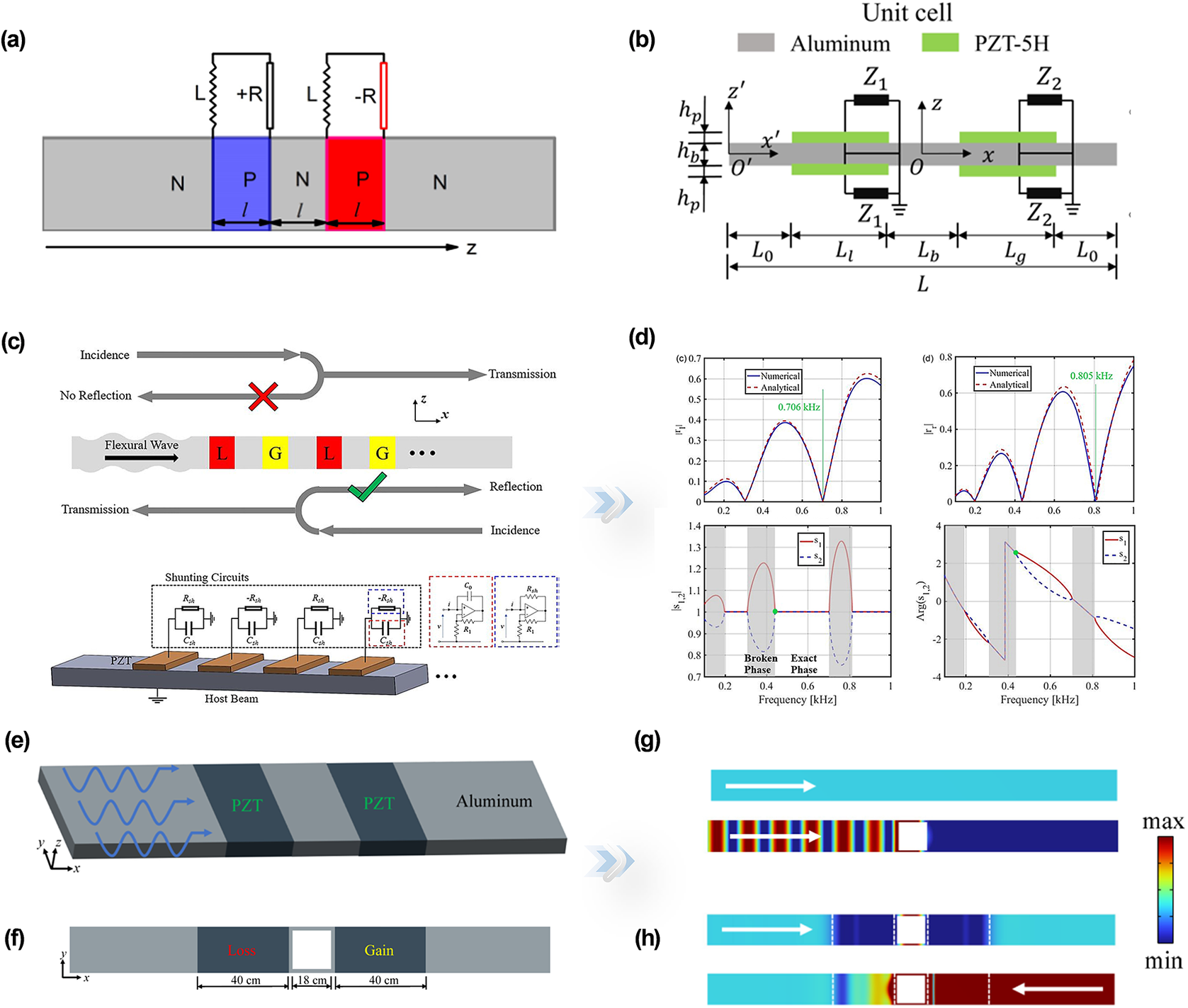
Figure 4. (a) The PT-symmetric metabeam can actively be tuned without alterations to its geometric configuration (Hou and Assouar, Reference Hou and Assouar2018). (b) The piezoelectric PT-symmetric metabeam (Yi et al., Reference Yi, Ma, Xia, Negahban, Chen and Li2022). (c) Unidirectional reflectionlessness of PT-symmetric beam. (d) Calculated reflection coefficients, amplitude, and phase of eigenvalues in PT-symmetric metabeam (Wu et al., Reference Wu, Chen and Huang2019). (e) Schematic illustration of a metaplate. (f) Schematic illustration of a non-Hermitian metaplate with a hole. (g) Displacement fields of the metaplate and metaplate with hole respectively. (h) Displacement fields of the metaplate with piezoelectric materials (Cai et al., Reference Cai, Jin, Li, Zhu, Zhu, Rabczuk and Zhuang2023).
On the other hand, an increasing number of investigations have shown that energy cannot keep balance in the broken phase of PT. Eigenfrequencies become complex under non-Hermitian conditions, thus generating extraordinary wave phenomena, such as non-reciprocal wave transmission (Ghatak et al., Reference Ghatak, Mandal and Mandal2013; Peng et al., Reference Peng, Özdemir, Lei, Monifi, Gianfreda, Long and Yang2014; Gear et al., Reference Gear, Sun, Xiao, Zhang, Fitzgerald, Rotter and Li2017; Song et al., Reference Song, Wang and Wang2021). In fact, most of these extraordinary elastic-wave manipulations in non-Hermitian metamaterials are closely related to EP. Qian Wu et al. designed a piezoelectric PT-symmetrical metabeam that can realize unidirectional reflectionlessness (Wu et al., Reference Wu, Chen and Huang2019). Due to the fact that effective mass density is assumed to be real, the PT-symmetric condition in this structure is illustrated by the effective bending stiffness. Thus, to realize a complex effective bending stiffness, this structure induces non-Hermiticity by the piezoelectric system. As shown in Figure 4(c), two piezoelectric patches are bonded to the beam. Each patch is connected to an external circuit that includes a negative/positive resistor and a negative capacitor in parallel. Here, the gain component is composed of negative resistance, the loss component is provided by positive resistance, and the negative capacitance can amplify the gain/loss elements.
Furthermore, as depicted in Figure 4(d), the reflection coefficients pertaining to two distinct incident directions are presented. The markers of unidirectional reflectionlessness, delineated by green lines, manifest at frequencies of 0.706 kHz and 0.805 kHz. The phenomenon of unidirectional reflectionlessness in this context can also be analysed by scrutinizing the locus of EPs. A notable observation is that, at unidirectional reflectionless points, both the amplitudes and phases of the two eigenvalues are identical. Besides, the phase transition points are also exactly the unidirectional reflectionlessness points. These findings definitively establish a clear alignment between the unidirectional reflectionless points observed within the context of the non-Hermitian PT-symmetric beam and the conceptual framework of EPs. This assertion gains further substance from the demonstration of tunable EPs achieved by manipulating the parameters of the shunting circuit.
In addition, numerous recent studies have utilized PT symmetry and identified EPs in non-Hermitian metamaterials to explore increasingly peculiar elastic waves phenomena. Figure 4(e) depicts the design of a PT-symmetric metaplate utilizing piezoelectric elements (Cai et al., Reference Cai, Jin, Li, Zhu, Zhu, Rabczuk and Zhuang2023). Through the manipulation of these piezoelectric parameters, a striking phenomenon of unidirectional reflectionlessness becomes manifest. Expanding upon this concept, a metaplate featuring a perforation is introduced in Figure 4(f) to illustrate the concept of unidirectional cloaking. Given that the aperture inherently generates scattering waves and consequently influences the scattered field, the PT-symmetric system endeavours to counteract these scattering effects through the employment of EPs. Figure 4(g) visually portrays the displacement field across the metaplate. Notably, the wave field within the perforated metaplate exhibits disturbances when compared to an undisturbed solid plate. With the integration of piezoelectric materials, as demonstrated in Figure 4(h), the displacement field external to the piezoelectric region can be selectively restored in a unidirectional manner. It is imperative to underline that this cloaking effect finds its origins in the phenomenon of unidirectional reflectionlessness facilitated by EPs. In summary, the domain of non-Hermitian metamaterials, augmented by active control, offers unparalleled prospects for exploring the intricacies of wave amplification, energy harvesting, and the meticulous refinement of highly sensitive sensors.
Realization of the exceptional point
Analogous to electromagnetics and acoustics, EP plays an essential role in non-Hermitian elastic metamaterials (Shmuel and Moiseyev, Reference Shmuel and Moiseyev2020; Gupta and Thevamaran, Reference Gupta and Thevamaran2022; Wu et al., Reference Wu, Yi, Xia, Chen and Li2022; Gupta et al., Reference Gupta, Kurnosov, Kottos and Thevamaran2023). The scattering properties of elastic waves for non-Hermitian metamaterials with sharp changes around the EP have been verified in Figure 5(a) (Mokhtari et al., Reference Mokhtari, Lu, Zhou, Amirkhizi and Srivastava2020). In this section, we focus on the realization of unidirectional zero reflection by constructing the EP in the non-Hermitian system. In Figure 5(b), a viscoelastic generalized Maxwell model consisting of different resonators is proposed. The coupling between the viscoelasticity and resonators can widen the bandgap (Alamri et al., Reference Alamri, Li and Tan2018; Reference Alamri, Li, Mchugh, Garafolo and Tan2019). Besides, the asymmetry of the system is significantly affected by the mass of the oscillators. Notably, by controlling oscillator masses, this viscoelastic system also exhibits unidirectional zero reflection at the EP (Yi et al., Reference Yi, Li, Negahban, Xia and Zhu2022).
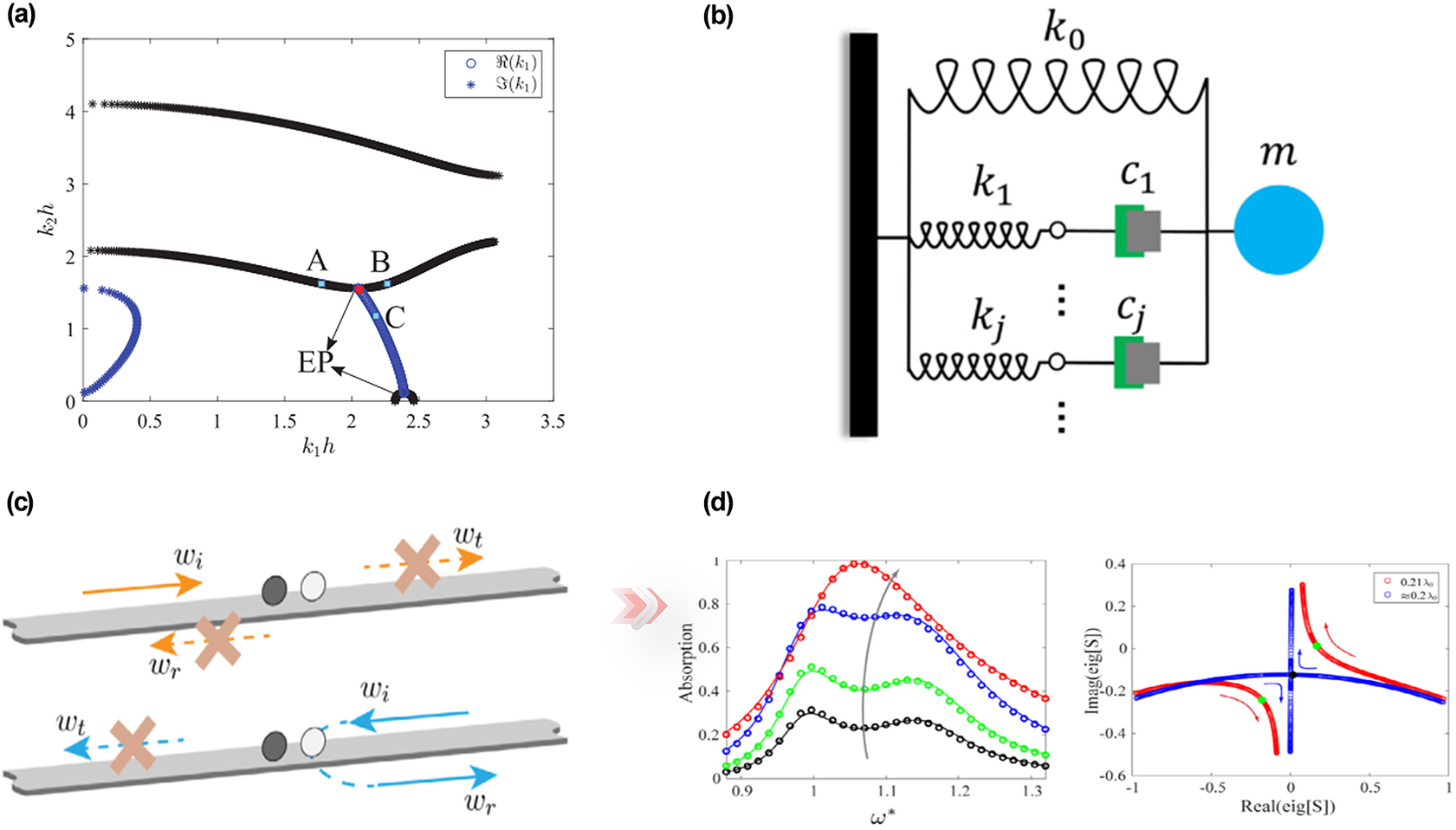
Figure 5. (a) EP occurs at the intersection of real branches and the branch with complex values (Mokhtari et al., Reference Mokhtari, Lu, Zhou, Amirkhizi and Srivastava2020). (b) The viscoelastic generalized Maxwell model (Yi et al., Reference Yi, Li, Negahban, Xia and Zhu2022). (c) Asymmetric transmission on a non-Hermitian metabeam. (d) Schematic of the EP at perfect absorption (Li et al., Reference Li, Yu, Iizuka and Lee2022).
More recently, an extremely asymmetric perfect absorption and reflection resonant scatterer has been proposed (Li et al., Reference Li, Liang, Wang, Lu and Liu2022). As exhibited in Figure 5(c), this structure consists of a pair of loss-induced asymmetrical resonant scatterers. Unidirectional reflection can be observed in two opposite incident directions. What is distinctive about the perfect absorption of this coupled resonator is the critical coupling condition, which means that the inherent losses in resonators equal the energy loss, which can be obtained by manipulating the intrinsic mechanical damping. As expected, interesting transmission characteristics can also be illustrated in eigenvalue curves. In Figure 5(d), double absorption peaks arise at smaller damping coefficients, whereas the two peaks start combining into a single peak at the optimum damping. Besides, when changing the distance of two resonators, eigenvalues coalesce at the optimum spacing distance and the system realizes perfect absorption.
Topological non-Hermitian metamaterials
In the field of elastic waves, topology has been employed to characterize different types of elastic waves based on their unique properties. The existing literature offers available methodologies to realize wave modulation in topological fields, including topological phase transitions and nontrivial topological states. At this point, the influence of topological phase control has been closely examined (Ghatak et al., Reference Ghatak, Mandal and Mandal2013; Peng et al., Reference Peng, Özdemir, Lei, Monifi, Gianfreda, Long and Yang2014; Gear et al., Reference Gear, Sun, Xiao, Zhang, Fitzgerald, Rotter and Li2017; Song et al., Reference Song, Wang and Wang2022; Gupta et al., Reference Gupta, Kurnosov, Kottos and Thevamaran2023). A soft elastic metamaterial shown in Figure 6(a) can realize dynamic tunability of topological states (Li et al., Reference Li, Zhao, Niu, Zhu and Zang2018). Moreover, it is worth noting that topologically protected wave propagation possesses robust defect-immune transport properties. One interesting aspect is that breaking reciprocity to mimic the quantum Hall effect (QHE) (Huckestein, Reference Huckestein1995; Zhang et al., Reference Zhang, Tan, Stormer and Kim2005) is a broad path to realize topologically protected wave propagation. For example, the broken space/time reversal symmetry provides a new prospect for obtaining the QHE. Figure 6(b) elucidates the nontrivial state, and it can realize the topologically protected elastic-wave edge mode when the time-reversal symmetry is broken (Nash et al., Reference Nash, Kleckner, Read, Vitelli, Turner and Irvine2015). In recent years, researchers have explored the possibility of topological protection in the absence of an applied magnetic field. In this field, the quantum spin Hall effect (QSHE) (Kane and Mele, Reference Kane and Mele2005b; Qi and Zhang, Reference Qi and Zhang2011) and the quantum valley Hall effect (QVHE) (Xiao et al., Reference Xiao, Yao and Niu2007; Pan et al., Reference Pan, Li, Liu, Zhu, Qiao and Yao2014) exhibit fascinating applications. Most remarkably, the QHE can be obtained by breaking the space-reversal symmetry, and it can be characterized by the generation of counter-propagating chiral edge states localized at the opposite edges of the material. In Figure 6(c), an elastic metamaterial plate generates a new local resonant bandgap that supports topological edge modes and illustrates the QVHE (Zhang et al., Reference Zhang, Li, Wang, Feng, Guan and Yao2020).
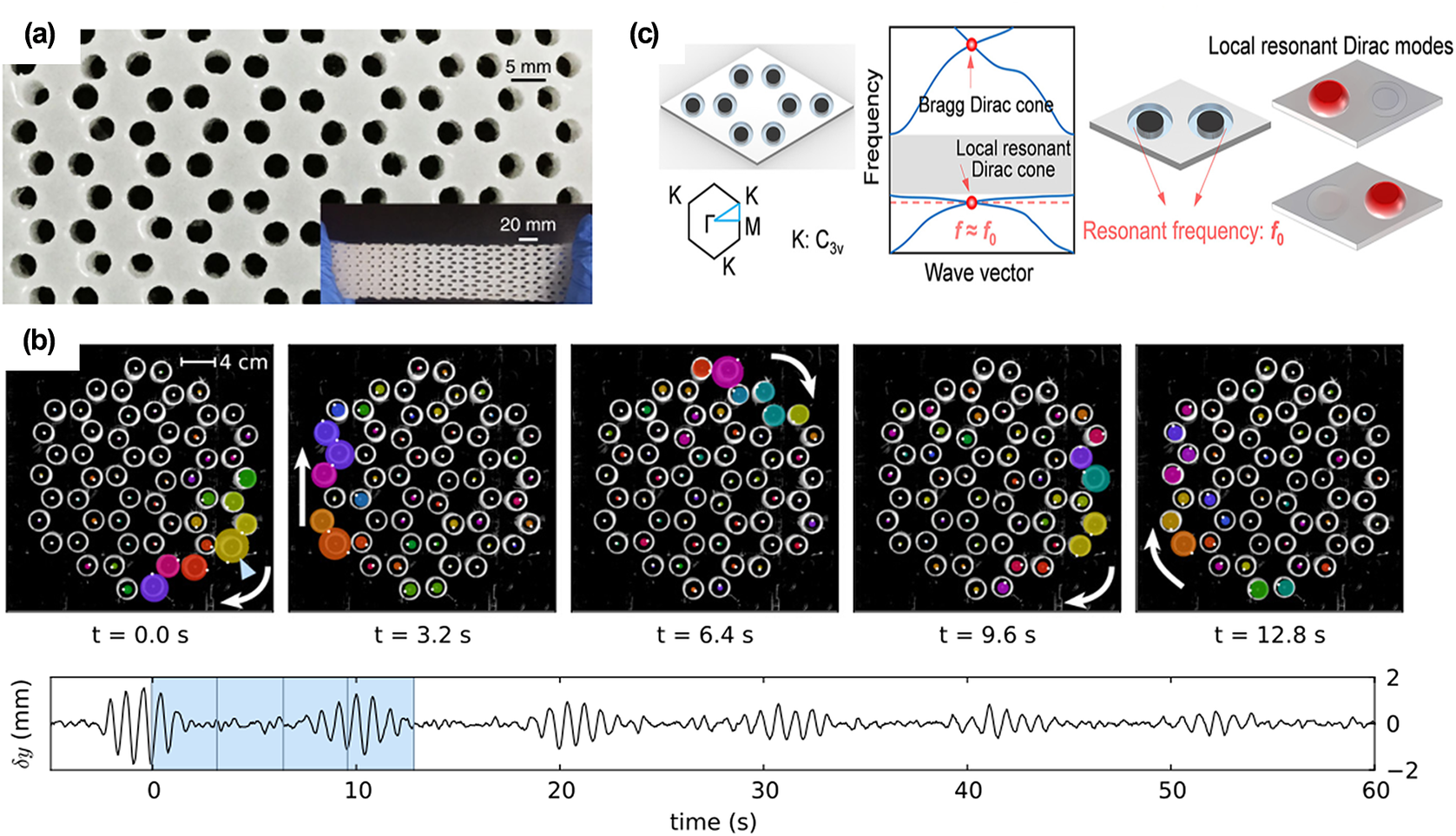
Figure 6. (a) Soft elastic metamaterials (Li et al., Reference Li, Zhao, Niu, Zhu and Zang2018). (b) Local resonant valley Hall insulator (Zhang et al., Reference Zhang, Chen, Zhang and Hu2020). (c) Unidirectional waveguide modes excited by a single-edge gyroscope (Nash et al., Reference Nash, Kleckner, Read, Vitelli, Turner and Irvine2015).
A further attractive concept that has expanded from quantum systems to classical waves is topological non-Hermiticity. More recently, along with the fusion of non-Hermitian and elastic waves, there has been an extensive focus on elastic topological structures within non-Hermiticity. The idea of combining the topology and non-Hermiticity in elastic waves has not only been obtained but also adapted in both theories and experiments (Zhang et al., Reference Zhang, Wu, Jin and Song2019; Tang et al., Reference Tang, Jiang, Ding, Xiao, Zhang, Chan and Ma2020; Riva et al., Reference Riva, Castaldini and Braghin2021; Wu et al., Reference Wu, Jin and Song2021). For example, a freestanding metabeam with non-Hermitian modulation can achieve unidirectional amplification or attenuation of wave propagation (Figure 7(a)). Furthermore, the spectrum shows that the elastic modulus is related to the topological index, and this phenomenon results in the localization of vibrational modes (Figure 7(b)) (Chen et al., Reference Chen, Li, Scheibner, Vitelli and Huang2021). On the basis of these related achievements, we set out to clarify the non-Hermitian manipulation of the topological edge modes. Figure 7(c) shows the design of a 1D trimerized model consisting of a resonant plate and linking beam (Fan et al., Reference Fan, Gao, An, Gu, Chen, Huang and Su2022), where the topological edge modes can be caused by non-Hermiticity when damping layers are added to the structure. This may excite more explorations about the plentiful mechanisms between topology and non-Hermiticity. Moreover, other research has investigated the realization of topological edge modes. It explores the topological edge states under the Hermitian and non-Hermitian conditions, respectively (Fan et al., Reference Fan, Gao, An, Gu, Liang, Zheng and Liu2022). This system is able to maintain unanimous hopping strengths in unit cells and modulate nontrivial topologies by adjusting additional damping layers. The out-of-plane displacement field presented in Figure 7(d) illustrates the two edge modes localized at the two edges. On the other hand, a recent thesis evaluated a topological coupler with four ports with non-Hermiticity (Meng et al., Reference Meng, Wu, Shen, Liu, Liang, Zhang and Li2022). Combining the gain and loss control by the non-Hermiticity, highly efficient elastic-wave guiding with topological robustness was realized. In summary, the coupling between topology and non-Hermitian may be extended to further fields and offers more useful findings in sensing and signal processing.
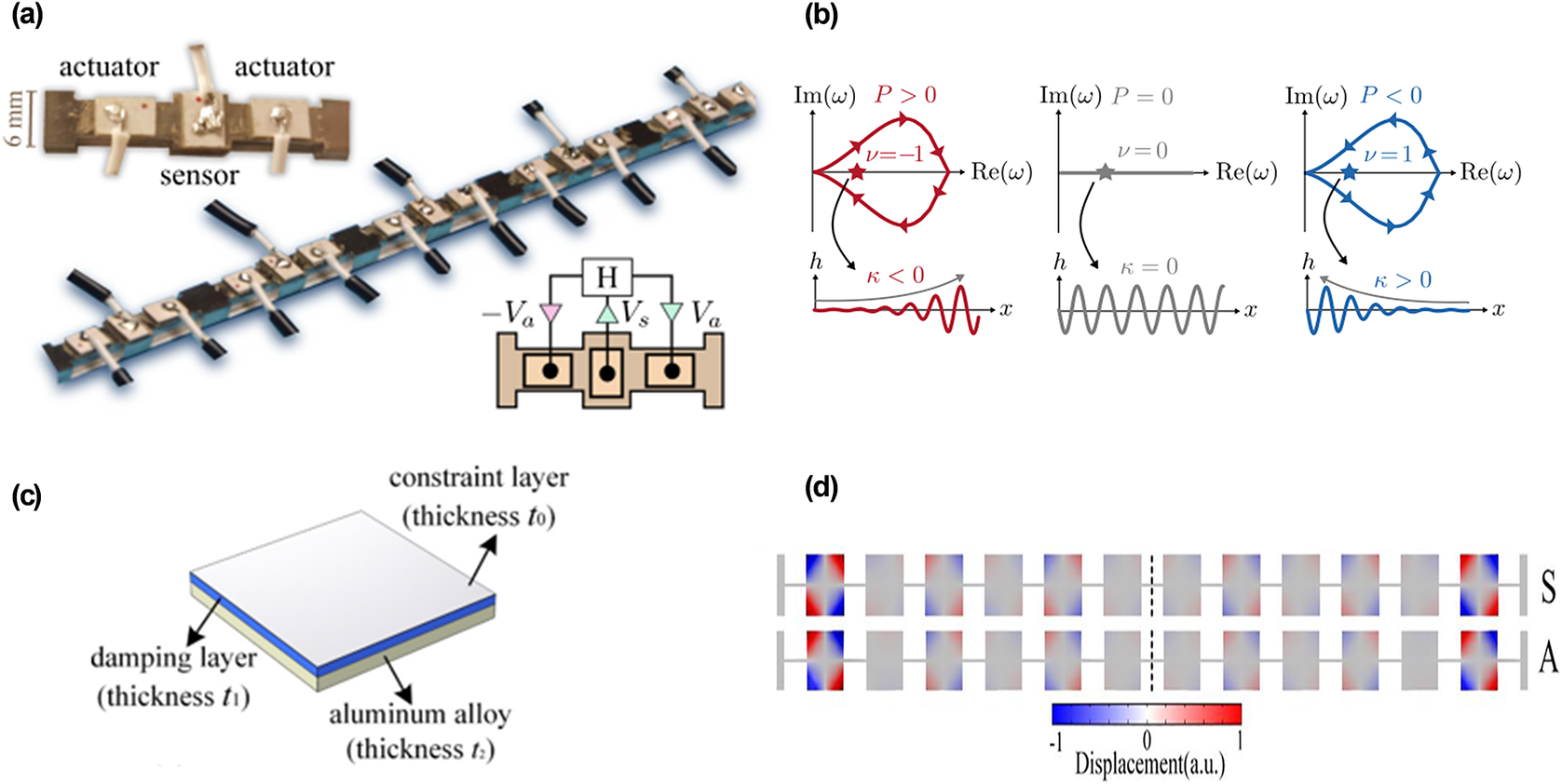
Figure 7. (a) A non-Hermitian metabeam with piezoelectric elements and electronic feed-forward control. (b) The presence of a localized mode (Chen et al., Reference Chen, Li, Scheibner, Vitelli and Huang2021). (c) Schematic of the composite plate from top to bottom: the tin foil constraint layer, the rubber damping layer, and the aluminium alloy host plate (Fan et al., Reference Fan, Gao, An, Gu, Chen, Huang and Su2022). (d) Out-of-plane displacement of the topological edge state (Fan et al., Reference Fan, Gao, An, Gu, Chen, Huang and Su2022).
Non-Hermitian elastic metasurfaces
In recent decades, the domain of metamaterials comprising subwavelength microstructures has witnessed remarkable and swift progress within the realm of elastic waves, facilitating the emergence of sophisticated wave control phenomena. However, due to the typically periodic characteristics, metamaterials are normally limited in bulky structures. Thus, aiming at structure simplification and application enrichment, a lightweight two-dimensional planar structure named metasurface is proposed. As shown in Figure 8(a), this structure possesses phase discontinuity and is hence able to manipulate wave propagation (Yu et al., Reference Yu, Genevet, Kats, Aieta, Tetienne, Capasso and Gaburro2011). As shown in Figure 8(b), Liu et al. introduced a source illusion device aimed at the manipulation of flexural Lamb waves through the utilization of elastic metasurfaces (Liu et al., Reference Liu, Liang, Liu, Diba, Lamb and Li2017). They have devised a comprehensive framework for the creation of source illusions targeting the
![]() ${A}_0$
mode Lamb waves. This framework showcased a range of versatile elastic illusion effects from all angles. Assessed through the lens of Huygens–Fresnel diffraction theory, this effect exhibited broadband characteristics and remained resilient even in the face of shifts in source positions.
${A}_0$
mode Lamb waves. This framework showcased a range of versatile elastic illusion effects from all angles. Assessed through the lens of Huygens–Fresnel diffraction theory, this effect exhibited broadband characteristics and remained resilient even in the face of shifts in source positions.
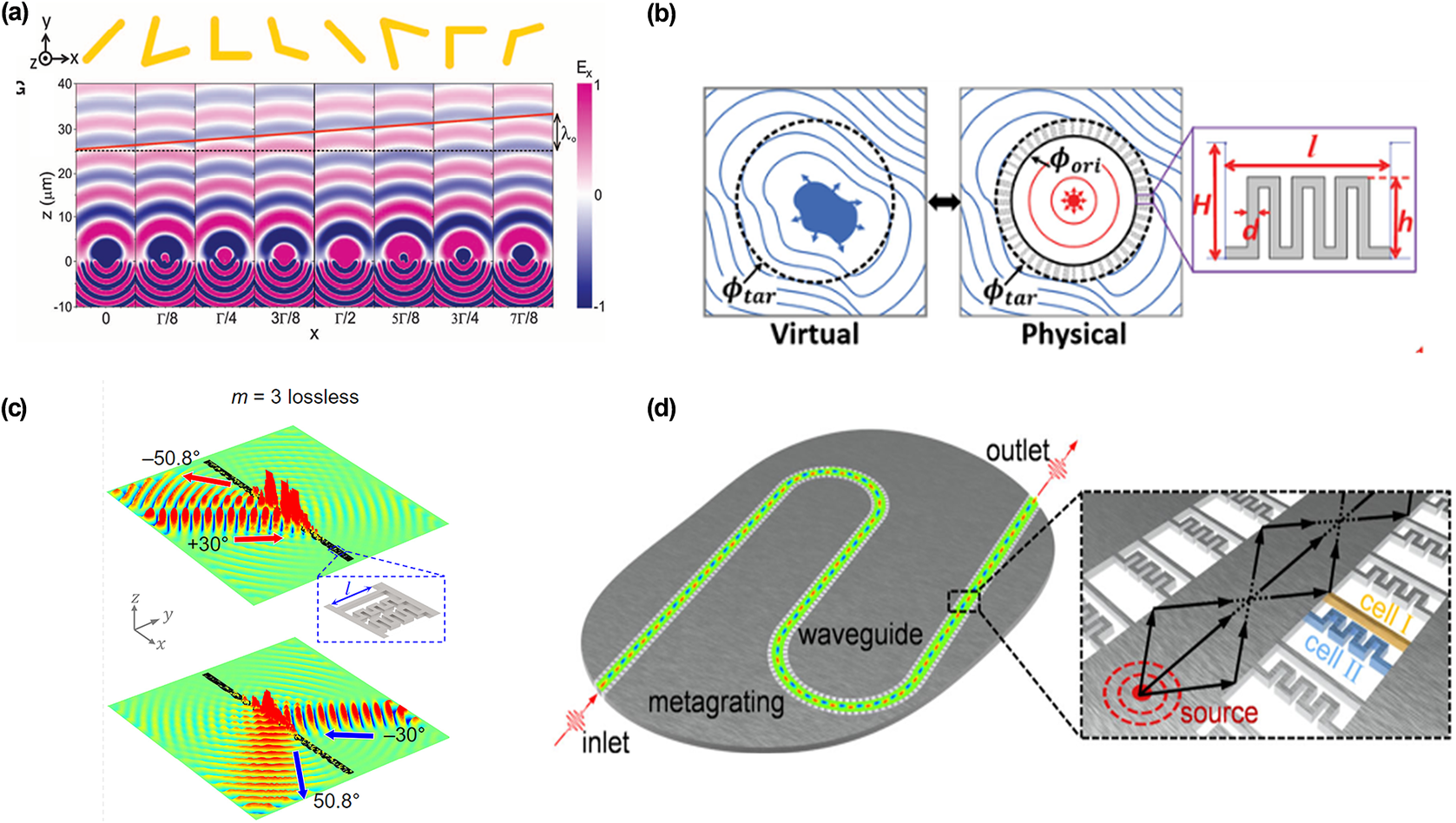
Figure 8. (a) Schematic of eight antennas and the transmission fields of the crosspolarized (Yu et al., Reference Yu, Genevet, Kats, Aieta, Tetienne, Capasso and Gaburro2011). (b) Schematic of making illusions using metasurfaces (Liu et al., Reference Liu, Liang, Liu, Diba, Lamb and Li2017). (c) Efficient asymmetric transmission in lossless metasurfaces (Li et al., Reference Li, Hu, Chen, Su, Liu, Zhao and Li2020). (d) An ultrathin waveguide routing along an arbitrary path in a plate and corresponding two layers of thin elastic metagratings (Hu et al., Reference Hu, Zhang, Su, Zhao, Li, Liu and Li2022).
A great deal of investigations provide plentiful applications in high-order diffractions (Liu and Jiang, Reference Liu and Jiang2018; Hou et al., Reference Hou, Fang, Li and Assouar2019; Hu et al., Reference Hu, Li, Liu and Li2023; Wang et al., Reference Wang, Cheng, Li and Li2023; Li et al., Reference Li, Cheng, Hu, Chen, Li and Li2024), negative refraction (Xie et al., Reference Xie, Wang, Chen, Konneker, Popa and Cummer2014; Willis, Reference Willis2016; Yang et al., Reference Yang, Qin, Zheng, Shen, Wang, Wang and Chen2018), and asymmetric propagation (Cao et al., Reference Cao, Xu, Assouar and Yang2018; Li et al., Reference Li, Hu, Chen, Su, Liu, Zhao and Li2020). For example, Figure 8(c) demonstrates a lossless metasurface that can achieve asymmetric transmission. It stems from the parity of multiple reflections against different diffraction orders (Li et al., Reference Li, Hu, Chen, Su, Liu, Zhao and Li2020). In addition, based on subwavelength metagratings, an ultrathin waveguide framework for omnidirectional wave trapping and efficient routing was proposed, as illustrated in Figure 8(d). Compared with metamaterial-based waveguides, this strategy exhibits absolute advantages in compact size and broadband wave routing (Hu et al., Reference Hu, Zhang, Su, Zhao, Li, Liu and Li2022).
Owing to its unique phase modulation, the challenges seem more attractive for combining non-Hermiticity and metasurface. Some factors affecting non-Hermitian metasurfaces have been explored. Similar to non-Hermitian elastic metamaterials, the related approaches are generalized in elastic metasurfaces. In stark contrast to the prevailing research paradigm rooted in Hermitian physics, a recent work embarks on an exploration of the uncharted territory of non-Hermitian elastic metamaterials, thus ushering in new frontiers within open quantum and classical systems characterized by gain or loss. As Figure 9(a) shows (Cheng et al., Reference Cheng, Hu and Li2024), this paradigm shift hinges on the introduction of non-Hermitian modulation, as embodied by the creation of the non-Hermitian metagrating (NHMG). The NHMG, characterized by its single type of subwavelength unit cell, exhibits remarkable characteristics under specific low-loss conditions, epitomizing the realization of perfect wave absorption (Figure 9(b)) and culminating in the establishment of a versatile design framework for NHMG materials, accommodating irregular and arbitrary shapes. This framework attests to the NHMG’s robust performance, underscoring its capacity to achieve omnidirectional and perfect absorption capabilities regardless of the boundary shape, rotation angle, and wave source location (Figure 9(c,d)). Consequently, this study not only diversifies the landscape of elastic-wave manipulation but also advances the fundamental understanding of non-Hermitian materials.
Figure 9. (a) Schematic diagram of the structure and function of NHMG. (b) Theoretical verification of perfect absorption in the NHMG and a perfectly absorbing NHMG unit cell. (c) The energy field distributions corresponding to NPU-shaped defects. (d) Experimental setup and experimental model (Cheng et al., Reference Cheng, Hu and Li2024). (e) Schematic of the piezoelectric non-Hermitian metasurface. (f) The realization of unidirectional focusing (Stojanoska and Shen, Reference Stojanoska and Shen2022).
Furthermore, investigations of EP on non-Hermitian elastic metasurfaces have provided design paradigms for elastic structural implementations. A recent work discusses the transmission characteristics of flexural waves in an asymmetric piezoelectric metasurface. The structure of this elastic metasurface is shown in Figure 9(e) (Stojanoska and Shen, Reference Stojanoska and Shen2022). The non-Hermitian degree can be adjusted by modulating the shunting resistance and the negative capacitance of the piezoelectric system. Under a lossless condition, the reflection and transmission amplitudes are equal in the opposite wave propagation directions, while under non-Hermitian conditions, the unidirectional zero reflection can be observed. This arises from the meticulous engineering of each unit cell to manifest an EP at the designated operational frequency. As a consequence, the metasurface attains a state of complete reflection suppression (Figure 9(f)). The real and imaginary parts of the eigenvalues coalesce at this critical value (i.e. EP). By accessing the focal length, the focusing of reflected waves can be obtained.
Although a few pioneering studies have been conducted, given that investigations of non-Hermitian metasurfaces are still in their infancy, existing analytical studies offer a new strategy for the design of non-Hermitian elastic meta-structures and structural wave control. Of equal significance, the aforementioned designs lay a foundation for potential research endeavours aimed at harnessing wave-related applications, including but not limited to structural health monitoring and nondestructive testing. Furthermore, this paves a natural path towards delving into the realm of non-Hermitian systems and their implications for these applications.
Skin effect in non-Hermitian meta-structures
Bulk-boundary correspondence in a non-Hermitian system
Ever since the development of condensed matter physics has brought cutting-edge research hotspots, a growing body of researchers has found that the electrons and atoms in quantum physics are able to form particular structures and exhibit unique properties. Hence, based on the novel phenomena of quantum states, numerous fundamental theories such as topological state, density matrix, and wave function have been proposed (Landau and Lifshitz, Reference Landau and Lifshitz1980; Anderson, Reference Anderson2018; Bouwmeester et al., Reference Bouwmeester, Pan, Mattle, Eibl, Weinfurter and Zeilinger1997; Kane and Mele, Reference Kane and Mele2005a, Reference Kane and Mele2005b; Bernevig et al., Reference Bernevig, Hughes and Zhang2006; Bernevig and Zhang, Reference Bernevig and Zhang2006; Konig et al., Reference Konig, Wiedmann, Brune, Roth, Buhmann, Molenkamp and Zhang2007; Hsieh et al., Reference Hsieh, Qian, Wray, Xia, Hor, Cava and Hasan2008; Breuer et al., Reference Breuer, Laine and Piilo2009; Yao et al., Reference Yao, Jiang, Gorshkov, Maurer, Giedke, Cirac and Lukin2012; Broadbent and Schaffner, Reference Broadbent and Schaffner2016; Streltsov et al., Reference Streltsov, Adesso and Plenio2017). In the quantum world, topology centres on the quantized model and its physical quantities, including topological structure, topological quantum circuit, and topology of porous material. Among these, topological meta-structures have garnered significant attention in the field of topological state research, primarily because they offer more efficient control over wave propagation. Moreover, topological band theory has achieved tremendous success with extensive literature, particularly on its boundary state and topological invariants.
The Bloch theorem plays a crucial role (Hasan and Kane, Reference Hasan and Kane2010; Qi and Zhang, Reference Qi and Zhang2011; Chiu et al., Reference Chiu, Teo, Schnyder and Ryu2016) in Hermitian topological meta-structure. As elaborated below, the Bloch wave functions give a description of the meta-structure band. Actually, in order to accurately describe their quantized behaviours, the concept of topological invariant is proposed to show topology properties. The topological invariant describes the overall space of structures, and structures with similar “genus” are topologically equivalent (Essin and Gurarie, Reference Essin and Gurarie2011). Besides, the topology represents the state of the substance. Thus, the topological phase of a system is delimited by topological invariants, like the Chern number (Hatsugai, Reference Hatsugai1993) and Winding number (Yin et al., Reference Yin, Jiang, Li, Lü and Chen2018). The Chern number is treated as the integral of berry curvature over the Brillouin zone, and it can illustrate the QHE, while the Winding number is capable of determining how many times a curve wraps around a specific point. Specifically, the curve should be closed and denoted as
![]() $C(t)$
, where
$C(t)$
, where
![]() $t$
ranges from
$t$
ranges from
![]() $0$
to
$0$
to
![]() $2\pi$
. Choose a point
$2\pi$
. Choose a point
![]() ${z}_0$
in the complex plane and the Winding number can be calculated as:
${z}_0$
in the complex plane and the Winding number can be calculated as:
![]() $W\left(C,{z}_0\right)=\left(1/2\pi i\right)\oint C\; dz/\left(z-{z}_0\right)$
, where ∮ represents the contour integral, which means integrating around the closed curve
$W\left(C,{z}_0\right)=\left(1/2\pi i\right)\oint C\; dz/\left(z-{z}_0\right)$
, where ∮ represents the contour integral, which means integrating around the closed curve
![]() $C$
,
$C$
,
![]() $dz$
is the differential element along the curve, and
$dz$
is the differential element along the curve, and
![]() $z$
is the parameter representing a point on the curve
$z$
is the parameter representing a point on the curve
![]() $C$
.
$C$
.
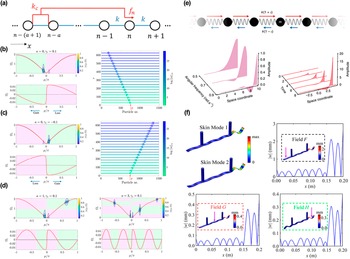
As shown in Figure 10, the BBC in the Hermitian system is an essential principle under open boundary conditions (OBCs). A significant milestone in the research of boundary states is that topologically protected boundary states become more stable and possess quantized features. As Figure 11(a) shows, in Hermitian systems, the boundary states under OBCs can be described by the topological invariants in periodic boundary conditions (PBCs). In non-Hermitian systems, open boundary states are completely different from periodic boundary states, which means the failure of BBC (Deng and Yi, Reference Deng and Yi2019; Jin and Song, Reference Jin and Song2019; Kunst and Dwivedi, Reference Kunst and Dwivedi2019; Lee et al., Reference Lee, Li and Gong2019; Yang et al., Reference Yang, Cao and Zhai2022). In Hermitian systems, the eigenstates under the open boundary represent the linear superpositions of Bloch waves under the periodic boundary, whereas in non-Hermitian systems, eigenstates decay exponentially and localize near the boundary. This phenomenon in the non-Hermitian system is called the “non-Hermitian skin effect” (Liang and Huang, Reference Liang and Huang2013; Lee, Reference Lee2016; Leykam et al., Reference Leykam, Bliokh, Huang, Chong and Nori2017; Alvarez et al., Reference Alvarez, Vargas and Torres2018; Kunst et al., Reference Kunst, Edvardsson, Budich and Bergholtz2018; Yao et al., Reference Yao, Song and Wang2018; Lee et al., Reference Lee, Li and Gong2019; Lee and Thomale, Reference Lee and Thomale2019; Scheibner et al., Reference Scheibner, Irvine and Vitelli2020; Zhang et al., Reference Zhang, Yang, Ge, Guan, Chen, Yan and Jia2021; Mandal et al., Reference Mandal, Banerjee and Liew2022; Xiao and Chan, Reference Xiao and Chan2022).
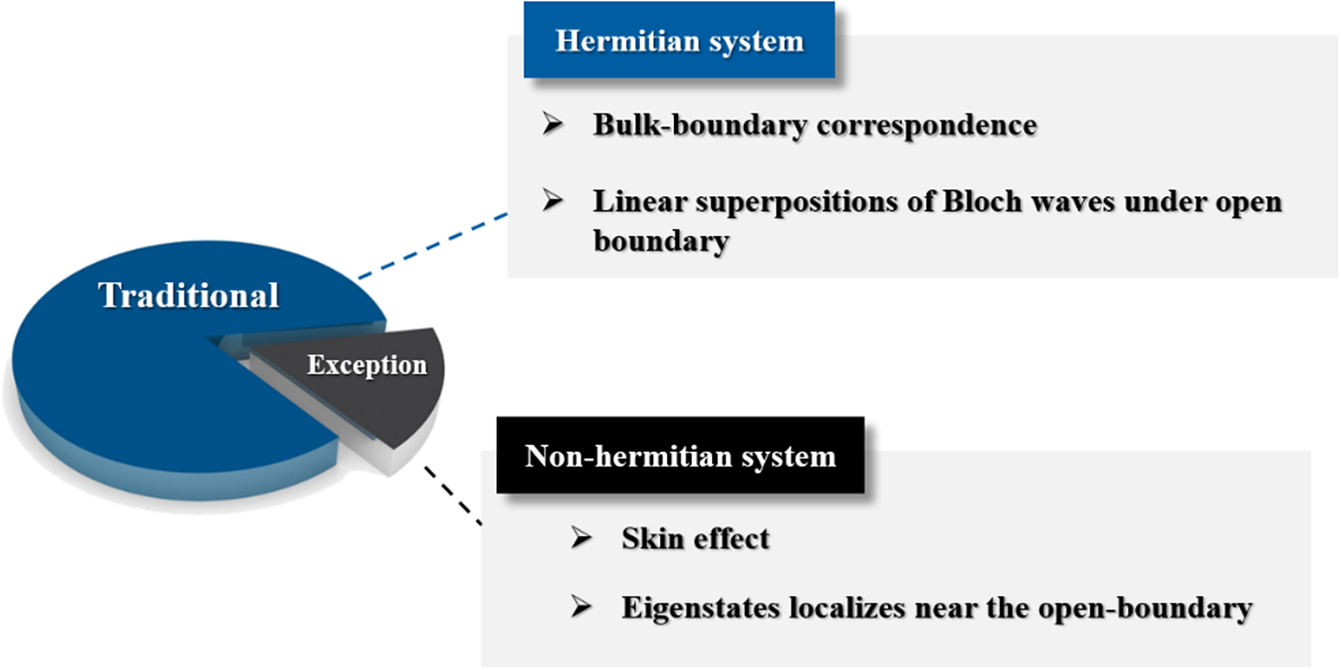
Figure 10. Different bulk-boundary states of Hermitian and non-Hermitian systems.
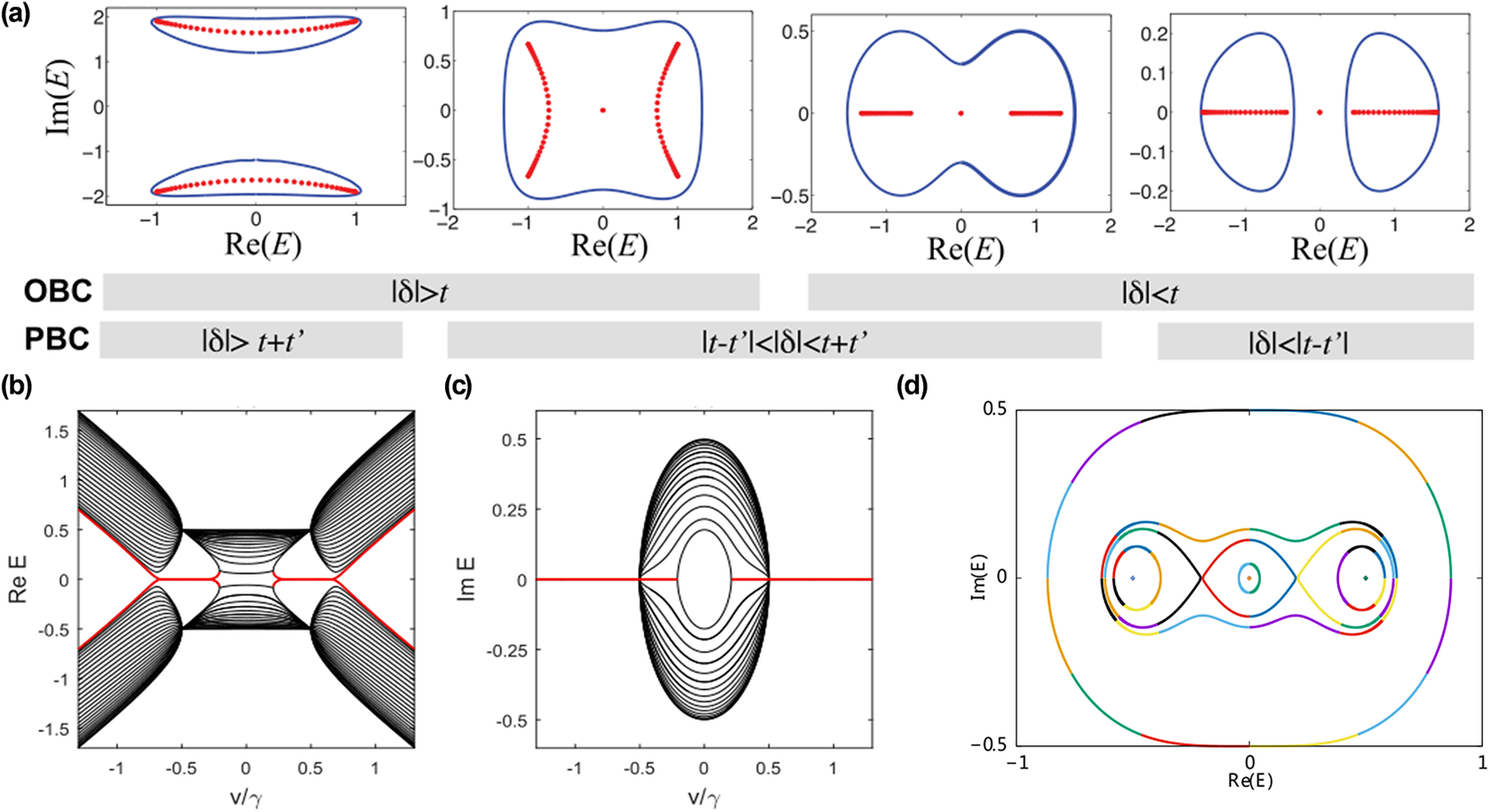
Figure 11. (a) Eigenspectra in different boundary conditions and topological phases (Longhi, Reference Longhi2019). (b) Real and (c) imaginary parts of the spectrum for an open chain (Lee, Reference Lee2016). (d) The traces of the eigenvalues (Xiong, Reference Xiong2018): the Hamiltonian encounters EPs and the alternation of eigenvalues splits into three unconnected loops.
Due to the disparity of boundary states in non-Hermitian systems, an increasing number of literature recognizes the crucial role of non-Bloch BBC in regulating non-Hermitian meta-structures. The breakdown of BBC has been demonstrated in a series of research (Lee, Reference Lee2016; Alvarez et al., Reference Alvarez, Vargas and Torres2018; Xiong, Reference Xiong2018). Lee (Reference Lee2016) proposed that the non-Hermiticity breaks the usual BBC that can be modified in a non-Hermitian system. Figure 11(b) and (c) show the real and imaginary parts of the spectrum for an open chain. Here the zero-energy state originates from non-Hermiticity. Further, in order to observe special phenomena of boundary states, Xiong analytically solved the non-Hermitian Hamiltonian of the Hatano–Nelson model (Xiong, Reference Xiong2018). This model can obtain the OBC by eliminating the hopping strength between the two ends of the chain. In this tight-binding model, the topological invariant generally represents the Winding numbers, and the topological invariant is encoded in the traces of the eigenvalues. In Figure 11(d), as the length of the chain is increased and the hopping strength r is changed, the Hamiltonian will encounter EPs and change its topological traces. Thus, this physical characteristic makes the spectrum topology different for chains with and without boundaries.
Moreover, there is an urgent need to address the challenge that the “non-Hermitian skin effect” necessarily redefines topological invariants in a generalized Brillouin zone (Shen et al., Reference Shen, Zhen and Fu2018; Yao et al., Reference Yao, Song and Wang2018; Kawabata et al., Reference Kawabata, Okuma and Sato2020). One work starts with constructing and solving the non-Hermitian Su–Schrieffer–Heeger (SSH) model (Zeuner et al., Reference Zeuner, Rechtsman, Plotnik, Lumer, Nolte, Rudner and Szameit2015; Weimann et al., Reference Weimann, Kremer, Plotnik, Lumer, Nolte, Makris and Szameit2017; Lieu, Reference Lieu2018). As Figure 12(a) shows (Shunyu and Wang, Reference Shunyu and Wang2018), the Bloch Hamiltonian of the model is
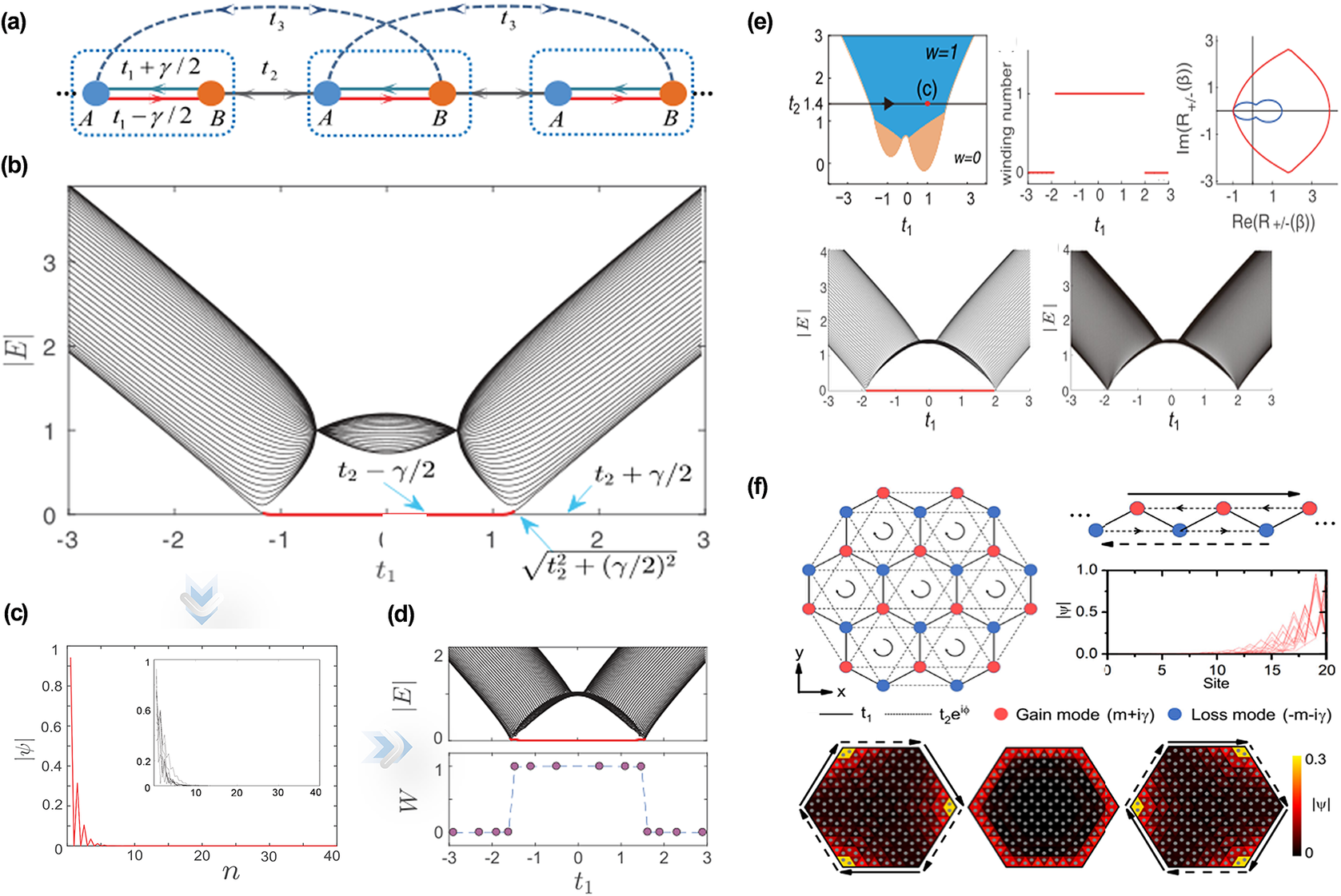
Figure 12.
(a) Schematic of non-Hermitian SSH model. (b) Numerical spectra
![]() $E$
of an open chain model. (c) The eigenstates are localized near the boundary. (d) Spectrum of open chain corresponding to topological invariants (Shunyu and Wang, Reference Shunyu and Wang2018). (e) Phase diagram and bulk-edge correspondence in a non-Hermitian SSH model (Yokomizo and Murakami, Reference Yokomizo and Murakami2019). (f) Hybrid skin topological modes and non-Hermitian Haldane model (Li et al., Reference Li, Yu, Iizuka and Lee2022).
$E$
of an open chain model. (c) The eigenstates are localized near the boundary. (d) Spectrum of open chain corresponding to topological invariants (Shunyu and Wang, Reference Shunyu and Wang2018). (e) Phase diagram and bulk-edge correspondence in a non-Hermitian SSH model (Yokomizo and Murakami, Reference Yokomizo and Murakami2019). (f) Hybrid skin topological modes and non-Hermitian Haldane model (Li et al., Reference Li, Yu, Iizuka and Lee2022).
Here,
![]() ${d}_x={t}_1+\left({t}_2+{t}_3\right)$
cosk,
${d}_x={t}_1+\left({t}_2+{t}_3\right)$
cosk,
![]() ${d}_y=\left({t}_2-{t}_3\right)$
sink, hopping parameters given by different
${d}_y=\left({t}_2-{t}_3\right)$
sink, hopping parameters given by different
![]() $t$
and the
$t$
and the
![]() ${\sigma}_{x,y}$
are Pauli matrices. Besides, based on the chiral symmetry of the SSH model, it can ensure the eigenvalues appear in (E;−E) pairs:
${\sigma}_{x,y}$
are Pauli matrices. Besides, based on the chiral symmetry of the SSH model, it can ensure the eigenvalues appear in (E;−E) pairs:
 $$\begin{align}{E}_{\pm }(k)=\pm \sqrt{d_x^2+{\left({d}_y+\frac{i\gamma}{2}\right)}^2}\end{align}$$
$$\begin{align}{E}_{\pm }(k)=\pm \sqrt{d_x^2+{\left({d}_y+\frac{i\gamma}{2}\right)}^2}\end{align}$$
First, taking
![]() ${t}_3=0$
to simplify the analysis, as Figure 12(b) shows, the EPs close at
${t}_3=0$
to simplify the analysis, as Figure 12(b) shows, the EPs close at
![]() $\left({d}_x,{d}_y\right)= \Big(\pm \gamma /2$
,
$\left({d}_x,{d}_y\right)= \Big(\pm \gamma /2$
,
![]() $0\Big)$
in PBCs, which means
$0\Big)$
in PBCs, which means
![]() ${t}_1={t}_2\pm \gamma /2\left(k=\pi \right)$
or
${t}_1={t}_2\pm \gamma /2\left(k=\pi \right)$
or
![]() ${t}_1=-{t}_2\pm \gamma /2\left(k=0\right)$
. However, in OBCs, the spectrum is noticeably different from that of the periodic boundary. Not only do the EPs close when
${t}_1=-{t}_2\pm \gamma /2\left(k=0\right)$
. However, in OBCs, the spectrum is noticeably different from that of the periodic boundary. Not only do the EPs close when
![]() ${t}_1$
=
${t}_1$
=
![]() $\sqrt{{t_2}^2+{\left(\gamma /2\right)}^2},$
but also the topology of H(
$\sqrt{{t_2}^2+{\left(\gamma /2\right)}^2},$
but also the topology of H(
![]() $k$
) cannot determine the corresponding boundary states. In order to gain familiarity with the Hermitian phenomenon in this model, a similarity transformation method is proposed when taking the equation as
$k$
) cannot determine the corresponding boundary states. In order to gain familiarity with the Hermitian phenomenon in this model, a similarity transformation method is proposed when taking the equation as
As shown in Figure 12(c), a bulk eigenstate of Hermitian
![]() $\overline{H}$
is extended, and eigenstates of
$\overline{H}$
is extended, and eigenstates of
![]() $H$
are localized at the end of the chain. Since this method is applicable only to
$H$
are localized at the end of the chain. Since this method is applicable only to
![]() ${t}_3=0$
case, a generalizable solution is proposed when
${t}_3=0$
case, a generalizable solution is proposed when
![]() ${t}_3\ne 0$
. Referring to the similarity transformation, the Bloch Hamiltonian is extended to the
${t}_3\ne 0$
. Referring to the similarity transformation, the Bloch Hamiltonian is extended to the
![]() $\beta$
complex plane that names the generalized Brillouin zone. Here, the Hamiltonian
$\beta$
complex plane that names the generalized Brillouin zone. Here, the Hamiltonian
![]() $H$
becomes the function of
$H$
becomes the function of
![]() $\beta$
. In Figure 12(d), when
$\beta$
. In Figure 12(d), when
![]() $\beta$
varies in a generalized Brillouin zone,
$\beta$
varies in a generalized Brillouin zone,
![]() $H\left(\beta \right)$
is able to describe the open boundary spectra and realize the BBC in non-Hermitian systems. To date, several conclusive studies of the skin effect and corresponding BBC in non-Hermitian meta-structures have been proposed. In Figure 12(e), a research (Yokomizo and Murakami, Reference Yokomizo and Murakami2019) analyses and reveals the characteristics of a 1D SSH model. Apart from this, in Figure 12(f), the gain-/loss-induced hybrid skin topological effect and the PT phase transition in skin topological modes are shown (Li et al., Reference Li, Yu, Iizuka and Lee2022).
$H\left(\beta \right)$
is able to describe the open boundary spectra and realize the BBC in non-Hermitian systems. To date, several conclusive studies of the skin effect and corresponding BBC in non-Hermitian meta-structures have been proposed. In Figure 12(e), a research (Yokomizo and Murakami, Reference Yokomizo and Murakami2019) analyses and reveals the characteristics of a 1D SSH model. Apart from this, in Figure 12(f), the gain-/loss-induced hybrid skin topological effect and the PT phase transition in skin topological modes are shown (Li et al., Reference Li, Yu, Iizuka and Lee2022).
Skin effect of non-Hermitian system with elastic-wave modulation
The above research is the fundamental theoretical physics of non-Hermitian skin effects. More spectacularly, an increasing number of researchers find that the investigations into skin effects have wider relevance for elastic-wave control in meta-structures. Thus, several works (Scheibner et al., Reference Scheibner, Irvine and Vitelli2020; Gao and Wang, Reference Gao and Wang2022; Zhou et al., Reference Zhou, Wu, Pu, Lu, Huang, Deng and Liu2023) have started to explore a wealth of strategies for the coupling between the skin effect and meta-structures and suggest potential possibilities for specific applications.
Rosa and Ruzzene proposed non-Hermitian elastic meta-lattice that are characterized by non-local feedback interactions (Rosa and Ruzzene, Reference Rosa and Ruzzene2020). They aimed to describe the relative skin effect through the analysis of a 1D meta-lattice. The meta-lattice includes equal masses
m
and is connected by springs of equal stiffness
k
. As Figure 13(a) shows, this model is derived by an external force and that interaction is proportional to the elongation of a spring at location
![]() $\boldsymbol{n}$
. This force can be expressed as
$\boldsymbol{n}$
. This force can be expressed as
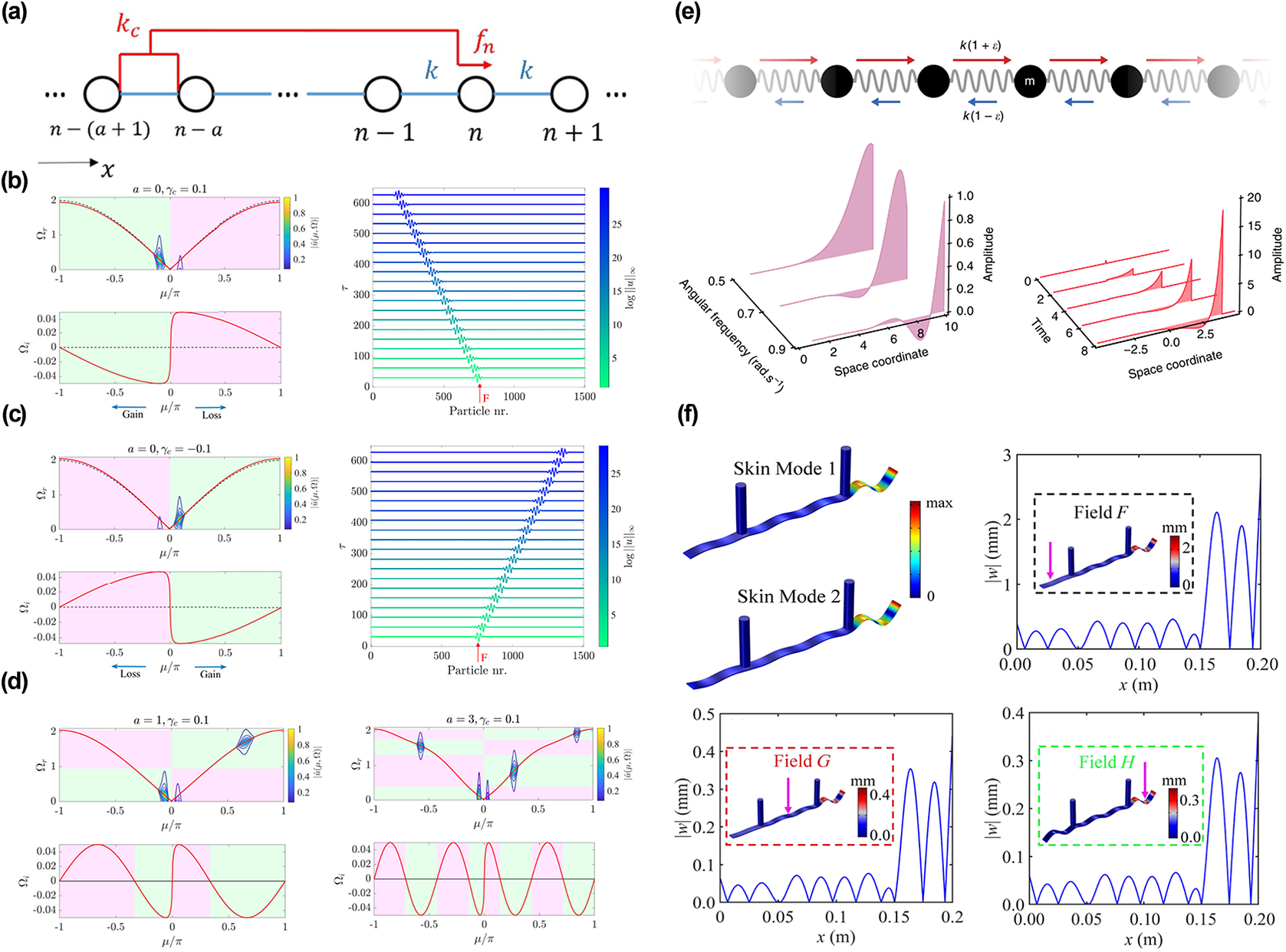
Figure 13. (a) One-dimensional lattice with feedback control interactions. (b)–(d) Non-reciprocal amplification and attenuation of waves in lattices with local feedback interactions (a = 0/1/3) (Rosa and Ruzzene, Reference Rosa and Ruzzene2020). (e) Analysing unidirectional wave amplification in a non-reciprocal mass-and-spring model (Brandenbourger et al., Reference Brandenbourger, Locsin, Lerner and Coulais2019). (f) The skin mode with non-reciprocity feedback and the realization of skin modes in different excitation locations (Cai et al., Reference Cai, Jin, Li, Rabczuk, Pennec, Djafari-Rouhani and Zhuang2022).
Here
![]() ${k}_c$
denotes the proportional control gain and
${k}_c$
denotes the proportional control gain and
![]() ${u}_n$
means the displacement of mass
${u}_n$
means the displacement of mass
![]() $n$
along the
$n$
along the
![]() $x$
axis. For a lattice of
$x$
axis. For a lattice of
![]() $N$
masses, the equations of motion can be written as follows:
$N$
masses, the equations of motion can be written as follows:
where
u
=
![]() ${\left[{u}_1,{u}_2,\dots, {u}_n\right]}^T$
, and
M
and
K
denote the mass and stiffness matrices, respectively. Then, a Bloch-wave solution is proposed by
${\left[{u}_1,{u}_2,\dots, {u}_n\right]}^T$
, and
M
and
K
denote the mass and stiffness matrices, respectively. Then, a Bloch-wave solution is proposed by
![]() $U{e}^{i\left(\omega t-\mu n\right)},$
where
$U{e}^{i\left(\omega t-\mu n\right)},$
where
![]() $\omega$
and
$\omega$
and
![]() $\mu$
, respectively, represent angular frequency and non-dimensional wavenumber, to substitute the equation that can yield the dispersion relation:
$\mu$
, respectively, represent angular frequency and non-dimensional wavenumber, to substitute the equation that can yield the dispersion relation:
Here,
![]() $\Omega =\omega /{\omega}_0,{\omega}_0=\sqrt{k/m}$
and
$\Omega =\omega /{\omega}_0,{\omega}_0=\sqrt{k/m}$
and
![]() ${\gamma}_c$
=
${\gamma}_c$
=
![]() ${k}_c$
/
${k}_c$
/
![]() $k$
. In addition, it is necessary to clarify exactly what is meant by the dispersion feature in the imaginary component. Actually, its positive wavenumbers are related to the loss (pink areas in Figure 13(b)), while the negative wavenumbers correspond to gain (green areas in Figure 13(b)). First, this work discusses the characteristics of a local control case (
$k$
. In addition, it is necessary to clarify exactly what is meant by the dispersion feature in the imaginary component. Actually, its positive wavenumbers are related to the loss (pink areas in Figure 13(b)), while the negative wavenumbers correspond to gain (green areas in Figure 13(b)). First, this work discusses the characteristics of a local control case (
![]() $a=0$
). Based on the non-reciprocity associated, the lattice with
$a=0$
). Based on the non-reciprocity associated, the lattice with
![]() ${\gamma}_c$
= 0.1 amplifies the left waves and attenuates the right waves (Figure 13(b)). In Figure 13(c), an opposite phenomenon can be observed with
${\gamma}_c$
= 0.1 amplifies the left waves and attenuates the right waves (Figure 13(b)). In Figure 13(c), an opposite phenomenon can be observed with
![]() ${\gamma}_c$
= −0.1. In Figure 13(d), when
${\gamma}_c$
= −0.1. In Figure 13(d), when
![]() $a>0$
, the transmission characteristics of the lattice are defined by non-local interactions. There will be two distinct regions of gain or loss for each wave propagation direction. In general, the number of non-reciprocal bands increases along with the higher value of
$a>0$
, the transmission characteristics of the lattice are defined by non-local interactions. There will be two distinct regions of gain or loss for each wave propagation direction. In general, the number of non-reciprocal bands increases along with the higher value of
![]() $a$
.
$a$
.
In view of the above research, non-reciprocity is achieved by combining the broken spatial symmetries and nonlinearities (Sounas and Alu, Reference Sounas and Alu2017; Wang et al., Reference Wang, Yousefzadeh, Chen, Nassar, Huang and Daraio2018; Lee et al., Reference Lee, Li and Gong2019). Meanwhile, breaking reciprocity inspires a wealth of nontrivial physics and significant applications. Thus, the obvious idea arises that non-reciprocal feedback plays a crucial role in the non-Hermitian skin effect. As Figure 13(e) shows, Brandenbourger et al. (Reference Brandenbourger, Locsin, Lerner and Coulais2019) designed a non-reciprocal robotic metamaterial. In non-reciprocal conditions, the solution shows exponentially localized standing waves or localized oscillatory standing waves with an exponential envelope. By virtue of non-reciprocal effects, the initial pulse is amplified along one propagation direction but attenuated along the opposite propagation direction. These phenomena realize the mechanical analogue of the non-Hermitian skin effect. Such a non-reciprocal case shows extreme asymmetry of angular displacement and asymmetric modes. In addition, a non-Hermitian metabeam proposed by Jin et al. is presented in Figure 13(f). This metabeam is enforced by a pair of external forces (Cai et al., Reference Cai, Jin, Li, Rabczuk, Pennec, Djafari-Rouhani and Zhuang2022). In this metabeam, one interesting phenomenon is the skin mode of elastic waves. Through imposing external forces (whose values are related to the velocities of the neighbouring pillar) on both sides of the metabeam, non-reciprocity feedback can be obtained. To be specific, the metabeam only allows the elastic waves to propagate in a single direction, and the responses are localized at one end. More notably, as Figure 13(f) shows, this skin mode, based on the non-reciprocity feedback, is immune to the excitation location.
In the context of the skin mode for the elastic-wave device reviewed here, the exploitation of the skin effect in elastic waves has received unprecedented interest. The above pioneering strategies provide promising avenues to achieve diverse applications such as broadband energy harvesting, communication, and sensing with higher sensitivity. Hence, we can envision that further developments of skin modes in elastic meta-structures may generate more extraordinary wave manipulation fashions and offer appealing potential applications.
Summary and outlook
Beyond the realm of Hermitian physics, non-Hermiticity has recently enabled, a surge of nontrivial phenomena and captured remarkable attention in both quantum and classical systems. Excitingly, taking into account non-Hermiticity in meta-structures has not only improved the wave-control accuracy but also provided new paradigms for extraordinary and intriguing wave manipulations. In this perspective, starting from electromagnetics and acoustics, we mainly focused on the up-to-date progress of non-Hermitian elastic meta-structures with a review of their extraordinary elastic-wave manipulations. The corresponding studies also highlighted this crucial component of non-Hermitian modulation, such as the phase break of PT-symmetric (Fang et al., Reference Fang, Gerard, Zhou, Ding, Wang, Jia and Li2021a; Cao et al., Reference Cao, Zhu, Wan, Zeng and Assouar2022), non-reciprocal feedback (Lau and Clerk, Reference Lau and Clerk2018; Clerk, Reference Clerk2022; Gao and Wang, Reference Gao and Wang2022), etc. Furthermore, non-Hermitian elastic meta-structures offer an ideal platform for the exploration of innovative wave phenomena within the domains of disorder, nonlinearity, and active control.
Up to now, the presence of non-Hermitian effects (loss/gain) has significantly impacted the mechanical behaviour of elastic meta-structures and their wave manipulation abilities. However, current research on gain design is relatively sparse. There is a lack of a systematic modulation scheme for structural design to provide gain factors, and experimental feasibility verification of non-Hermitian meta-structures is also deficient. On the other hand, in non-Hermitian metasurfaces, higher-order diffraction waves are particularly sensitive to the effects of gain/loss. Existing literature on controlling high-order diffraction waves under non-Hermitian conditions is relatively insufficient in terms of wave theory, analytical methods, and experimental approaches. In response to the aforementioned issues and challenges, we believe that embracing active methods holds the potential to broaden the scope of design and applications for non-Hermitian meta-structures. In particular, the quantitative introduction of gain/loss through piezoelectric and intelligent control to achieve precise manipulation of phase and amplitude is anticipated to offer new experimental avenues for non-Hermitian metasurfaces. This method may provide fresh design concepts for more efficient elastic guided wave control, thereby expanding the phenomenon of non-Hermitian elastic guided wave control.
Here, as a further step, based on the previous literature, we surmise the outlook for non-Hermitian elastic waves. While non-Hermitian meta-structures have been explored in the context of elastic waves, achieving accurate modulation of loss and flexible wave control is rather challenging. Considering future works in the exploration of non-Hermitian meta-structures, we expect that the coupling between non-Hermitian and elastic waves can be more beneficial in the case of transmission, reflection and absorption applications. As Figure 14 shows, from the perspective of physics, the exploration of PT-symmetric, wave amplification, non-reciprocity, nonlinearity, and skin effects may become research hotspots in non-Hermitian fields. In addition, the practice of these phenomena will enrich the applications of non-Hermitian meta-structures, such as single-mode oscillation, asymmetric reflection, unidirectional amplification, broadband non-reciprocity, signal power amplification, and transient skin effect. Furthermore, hybrid couplings between phase-broken PT-symmetric structures, non-local feedback mechanisms, and the utilization of high-order diffraction hold significant promise for enabling a wide array of efficient wave-manipulation applications in non-Hermitian meta-structures. In conclusion, further exploration in these fields holds the potential to broaden the horizons of non-Hermitian meta-structures, offering valuable strategies for advancing research in the realm of non-Hermitian investigations.
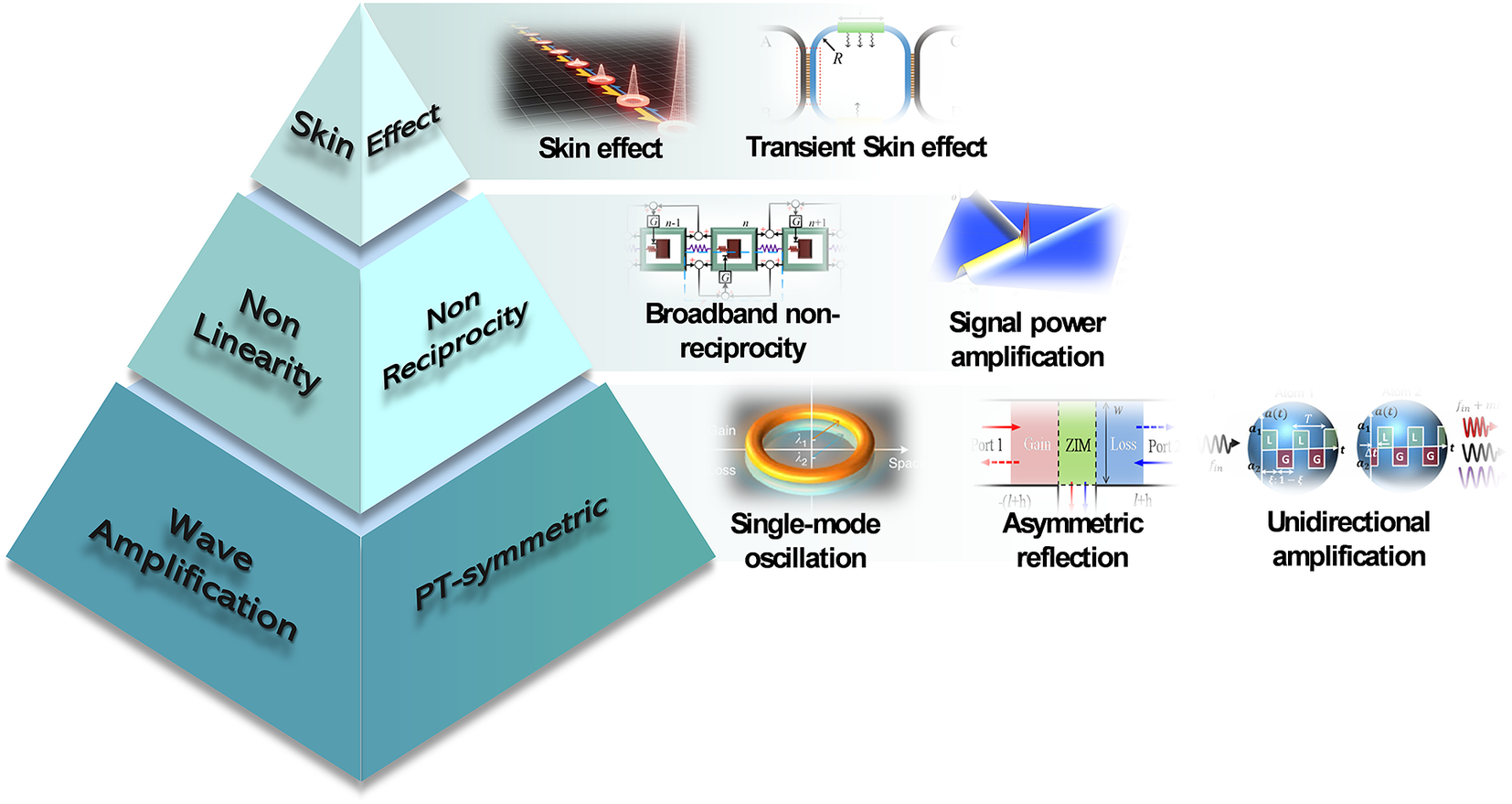
Figure 14. Vision for non-Hermitian system in elastic waves (Fu and Xu, Reference Fu and Xu2017; Nunes et al., Reference Nunes, Dias and Lyra2017; Lau and Clerk, Reference Lau and Clerk2018; Zhang et al., Reference Zhang, Li, Wang, Feng, Guan and Yao2020; Gao and Wang, Reference Gao and Wang2022; Gu et al., Reference Gu, Gao, Xue, Li, Su and Zhu2022; Liu et al., Reference Liu, Wei, Hemmatyar, Pyrialakos, Jung, Christodoulides and Khajavikhan2022; Zhang et al., Reference Zhang, Cui, Chen, Zhang and Chan2023).
Acknowledgements
The authors acknowledge the financial support from the National Natural Science Foundation of China (NSFC) (Grant Nos. 12272298, 12172271 and 12232001), Guangdong Basic and Applied Basic Research Foundation (No. 2024A1515011663), Natural Science Foundation of Chongqing (No. CSTB2023NSCQ-MSX0899).