^{page 417 note *} Instead of 2¹⁰ we find in the original 2⁵, and in the Collected Math. Papers 2⁸.

^{page 421 note *} The first two of these results, which follow from (α) and (β), there is no pressing reason for mentioning: it would have been equally pertinent to note that u=0. The third result Jacobi probably obtained (see Crelle's Journal, xv. p. 304) by taking in every possible way n-1 of the initiatory set of equations and deducing

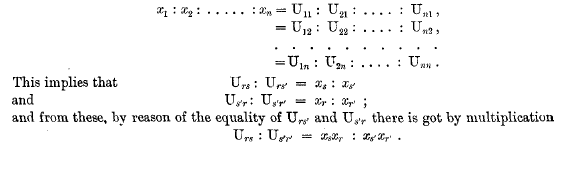
^{page 423 note *} See Philos. Magazine, ii.(1851)p. 406, and Cambridge and Dub. Math. Journ., vii. (1852) p. 52; or Sylvester's Collected Math. Papers, i. pp. 280, 284.

^{page 423 note †} On p.194 he says the Hessian of F(x, y) is “the determinant of the determinant, in respect to ξ and η, of

—an error which is repeated in the Collected Math. Papers.

^{page 424 note *} See Philos. Magazine, v. p. 122: or Collected Math. Papers, i. p. 591.

^{page 424 note †} It should be noted that this is of the Hessian as defined, that a₁ is expressible as a three-line determinant, and that the performance of the circular substitutions a ₁, b ₂, c ₃=b ₂, c ₃,a ₁, a ₂,b ₃, c ₁=b ₃, c ₁, a ₂, a ₃, b ₁, c ₂=b ₁, c ₂, a ₃, on the expressions for a₁, 3a₂, 3a₃gives us six other of the expressions.

^{page 429 note *} The reason given for the deduction U_rs= Nx₁x_s, which occurs in his presentation of Jacobi's proof of the year 1849, is disappointing.

^{page 430 note *} See (α)in Jacobi's proof of 1849.