Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T00:53:40.795Z Has data issue: false hasContentIssue false
  • English
  • Français

XX.—The Square Roots of a Linear Vector Function

Published online by Cambridge University Press:  15 September 2014

Frank L. Hitchcock
Get access

Extract

The equation in linear vector functions

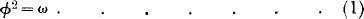
was proposed by Tait, and an elegant solution was obtained by him which does not require a determination of the axes of ω. He showed that upon this equation depends the separation of the pure and the rotational parts of a homogeneous strain. The problem appears to be interesting also from the point of view of algebraic analysis. The number and character of the solutions is more varied, given different types of the function ω, than we might at first suppose. In fact there are two forms which may be assigned to M such that the equation does not permit of solution. Otherwise the number of solutions.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 37 , 1918 , pp. 350 - 355
Copyright
Copyright © Royal Society of Edinburgh 1918

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 350 note * Quaternions, 3rd ed., chap. v, Ex. 17 (a), p. 144; solution, p. 298, note. Also in Kelland and Tait's Introduction to Quaternions, chap. x.

page 350 note † Proc. Roy. Soc. Edin., vol. xxxv, Part ii (No. 17), p. 170 (1915).

page 354 note * Comparing our results with Tait's solution (note 1), with which, of course, they are fully in accord, it is interesting to note that when φ has an infinite number of values, the denominator ω+g 1 in Tait's solution becomes ω+g, hence (ω+g 1)1 is indeterminate.

page 354 note † General conditions for the existence of a solution of the equation in matrices Xn = A are given by Kreis, H., Vierteljahrschrift Nat. Ges. Zurich, 1908, liii, p. 375.Google Scholar While his results hold for matrices of any order, their form renders them needlessly cumbrous for the present case. Cayley, by a method akin to Tait's in using the symbolic cubics of the known and unknown matrices, showed how the square root can be extracted, considering the general case (eight solutions) only. Proc. Roy. Soc. Edin., 1872, vii, p. 675.

page 355 note * See Tait's fascinatingly suggestive paper, Proc. Roy. Soc. Edin., vii, p. 311.