Article contents
XXII.—Borel's Integral and q-Series
Published online by Cambridge University Press: 15 September 2014
Extract
In his Theory of Infinite Series, Dr Bromwich gives an account of the recently developed theory of non-convergent and asymptotic series, so far as the arithmetical side of the theory is concerned. The connection between Borel's integral “sum” and Euler's well-known transformation
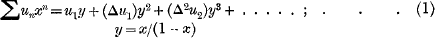
is discussed. Now, if we apply this transformation to such series, for example, as
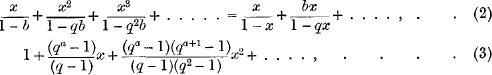
which are of great interest in the theory of Elliptic Functions, we obtain results which may be described as formless, or at least of such complexity, owing to the mixture of q-factorials (1 − qn)! with ordinary factorials n!, that the resulting series are practically useless so far as the possibility of applying further transformations is concerned.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1910
References
page 379 note * Trans. Cambridge Phil. Soc., vol. xix., 1904, p. 297.
page 380 note * Bulletin Amer. Math. Soc., vol. xiv., 1908, p. 485 (International Congress, Rome, 1908).
- 1
- Cited by


