Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T13:02:37.780Z Has data issue: false hasContentIssue false
  • English
  • Français

XVIII.—The Invariant Theory of Forms in Six Variables relating to the Line Complex

Published online by Cambridge University Press:  15 September 2014

H. W. Turnbull
Get access

Extract

It is well known that the Plücker coordinates of a straight line in ordinary space satisfy a quadratic identity

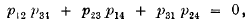
which may also be considered as the equation of a point-quadric in five dimensions, if the six coordinates Pij are treated as six homogeneous coordinates of a point. Projective properties of line geometry may therefore be treated as projective properties of point geometry in five dimensions. This suggests that certain algebraic theories of quaternary forms (corresponding to the geometry of ordinary space) can best be treated as algebraic theories of senary forms: that is, forms in six homogeneous variables.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 46 , 1927 , pp. 210 - 222
Copyright
Copyright © Royal Society of Edinburgh 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 211 note * Cf. Turnbull, , Proc. London Math. Soc., 2, 18 (1918), 69–84Google Scholar (72)

page 215 note * Ueber die Complex-flächen und die Singularitätenflächen der Complexe, Math. Ann., 5 (1872)Google Scholar. Cf. Jessop, Line Complex (Cambridge, 1903), 321–323.

page 216 note * A proof of this theorem will shortly appear in the Proc. London Math. Soc.

page 218 note * The factor (u A B C u) behaves like a ternary bracket factor (a b c) : so there is one term for each group A B C.

page 220 note * Cf. Grace and Young, Algebra of Invariants (Cambridge, 1903), pp. 275, 276. Turnbull, Proc. London Math. Soc., 2, 18 (1918), 69–94Google Scholar (73).