No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
Determinants whose elements are themselves determinants made their appearance at a very early stage in the history of the subject, the first foreshadowing of them being contained in Lagrange's “équation identique et très remarquable” of 1773, namely,
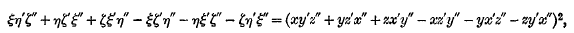
where

This, viewed as a result in determinants, is a case of Cauchy's theorem of 1812 regardingthe adjugate, and the adjugate of course is an instance of the special form to which we have now come. Jacobi's theorem regarding any minor of the adjugate has a like history and may be similarly classified. Passing from the case of the adjugate, where each element is a primary minor of the original determinant, Cauchy also considered the determinants of other “systèmes dérivés,” that is to say, the determinants whose elements are the secondary, ternary, … minors of the original, and gave the theorem that the product of the determinants of two “complementary derived systems” is a power of the original determinant, the index of the power being 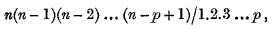 where n is the order of the original determinant and p the order of each element of one of the “derived systems.”
where n is the order of the original determinant and p the order of each element of one of the “derived systems.”
page 197 note * They are numbered xx., xxi., xli., xlii, in my History.
page 198 note * Proc. Roy. Soc. Edinburgh, xxv., p. 929.
page 200 note * θm was actually a misprint. Sylvester himself had to draw attention to it a year later in the Cambridge and Dub. Math. Journ., viii. p. 61.
page 202 note * See especially line 8 from bottom of p. 61, where in every case m should be m − 1.
page 205 note * And knowing this he might have indicated another mode of proving Cauchy's extended multiplication-theorem. For example:

page 209 note * Some of the pages of Spottiswoode dealt with in the foregoing are, by reason of misprints and other neglects, not easy reading. On p. 360 there are at least nine misprints.