No CrossRef data available.
Article contents
XL.—On Fourier's Repeated Integral
Published online by Cambridge University Press: 15 September 2014
Extract
§1. Pringsheim has recently reopened the question as to the circumstances under which Fourier's repeated integral exists and represents the function to which it corresponds. In its simplest form the theorem concerning this integral asserts that, with provisos to be specified—
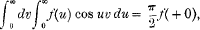
ƒ( + 0) being the unique limit, supposed to exist, of ƒ(u) as u approaches the value zero. From this equation, indeed, the remainder of the theory follows immediately. If it is to be true, certain conditions must be satisfied at the origin, at infinity, and in the finite part of the range of values of the independent variable. Till Pringsheim's paper appeared, the only condition known to be sufficient at infinity was of a very special character, requiring no less than the absolute integrability of the function at infinity.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1912
References
page 559 note * Pringsheim, A, “Ueber neue Giiltigkeitsbedingungen fur die Fouriersche Integral - formel,” (1909), Math. Ann., lxviii. pp. 367–408.Google Scholar
page 565 note * For the general form of the theorem here used see W. H. Young, “On a Theorem in the Harnack Integration of Series” (1910), § 3, Mess. Math., p. 105.
page 567 note * I use the symbol Llt to denote a possible plurality of limits, and Lt to denote an unique limit, known to exist.
page 568 note * Fatou, P., “Séries trigonométriques et Séries de Taylor,” 1905, Acta Math., xxx. pp. 335–400 Google Scholar; also Lebesgue, H., “Sur les integrates singnlieres,” 1910, Ann. de Toulouse, p. 90.Google Scholar
page 568 note † For this known result see, for instance, my paper on “Functions of Bounded Variation,” 1910, Quart. Journ., p. 82.
page 574 note * See Pringsheim, , loc. cit., pp. 375–6.Google Scholar
page 574 note † Fatou, loc. cit. Harnack, , Math. Ann., xix. (1882), p. 225.Google Scholar
page 574 note ‡ Pringsheim, A., Münch. Ber., 30 (1900), p. 63.Google Scholar
page 575 note * W. H. Young, “On the Integration of Fourier Series” (1910), Theorem 2, presented to the London Mathematical Society.
page 577 note * W. H. Young, “On the Theory of the Application of Expansions to Definite Integrals,” presented to the London Mathematical Society.
page 579 note *
There is a certain want of clearness on this point in Pringsheim's remarks on p. 397, as to his condition b
∞, referred to again on p. 400 ; if g(u) is only of bounded variation, not monotone, the existence of the integrals 
entails that 
but it is not a consequence of it.
page 581 note * This includes that case of Pringsheim's theorem, loc. cit., p. 399, § 5, in which the first of Pringsheim's conditions at infinity (p. 391) is satisfied by one of the factors of the integrand. The other factor is, in consequence of Pringsheim's further assumptions, a bounded function of all the variables.
page 581 note †
This may lie compared with a theorem given by Michel Plancherel on p. 42 of his “Contribution à l'étude de la représentation d'une fonction arbitraire par des intégrates définies,” 1910, Rend, di Palermo, xxx. pp. 1–47. In Plancherel's theorem 
exists, instead of, as here, 
page 583 note * Loc. cit., supra, § 17.